船舶可倾瓦推力轴承工况参数对润滑特性的影响∗

陈 泷 朱汉华 杨景怿 邹琪林 李博伦

（1.武汉理工大学交通与物流工程学院 湖北武汉 430063；2.武汉理工大学船海与能源动力工程学院 湖北武汉 430063）

在船舶动力系统中，推力轴承是船舶推进轴系中的关键部件。推力轴承的润滑性能很大程度上决定了船舶运行的稳定性和安全性。随着航行能力、机动性和安全性等要求的不断提高，推力轴承性能及稳定性受到高度关注［1］。

近年来国内外一些学者对推力轴承的润滑性能开展了研究。屈波等人［2］针对蓄能机组推力轴承，根据流固耦合理论研究了不同油膜厚度以及轴瓦倾角等因素对轴承压力分布的影响，发现随着倾角增大，油膜压力增大且最大油膜压力向轴瓦出油端偏移。GHERCA等［3］利用有限元法对在稳态和瞬态润滑状态下运行的流体动压推力轴承进行建模，分析了稳态和瞬态下推力轴承润滑性能的差异以及不同运行工况条件下，转子纹理对推力轴承润滑特性的影响。HANAWA等［4］提出了一种具有多孔结构的水润滑静压推力轴承并研究了其静态特性。SOKOLOV 等［5］建立了周期热弹性流体动力学模型，研究了推力轴承的进油温度对油膜厚度、轴承功耗、油膜承载力等静态润滑参数的影响。LIU 和JIANG［6］研究了转速和偏心率影响下水润滑静压推力轴承的温升特性，结果表明随着偏心率和转速的增大，油膜温度显著提高。魏士杰等［7］以船用动压可倾瓦推力轴承为例，研究了润滑油水侵对推力轴承润滑性能的影响，并结合黏温方程得到了不同含水量下推力轴承的静态润滑性能参数。王玉君等［8］建立了织构型非金属水润滑推力轴承的弹流动压润滑模型，对比分析了不同轴承材料对推力轴承润滑性能以及最优织构参数的影响，为水润滑推力轴承选型优化提供了依据。张赣波等［9］基于流体动压润滑理论分析了可倾瓦推力轴承的动态润滑特性，并分析了转速对推力轴承动态润滑特性变化规律的影响。WINKLER 等［10］基于有限元弹流润滑模型以及局部Archard 型磨损模型构建了混合弹流动压润滑模型，研究了不同载荷对推力滚子轴承润滑性能的影响。田佳彬等［11］建立了可倾瓦推力轴承瞬态热流体动压润滑模型，设计了几种不同的瓦面形貌，分析了不同瓦面形貌参数对推力轴承动润滑特性的影响。

虽然目前关于船舶可倾瓦推力轴承润滑特性已开展了相关研究工作，但大部分研究仅考虑单一因素对推力轴承润滑性能的影响，并且大部分都是关于稳态润滑特性的研究，涉及到瞬态润滑特性的相关研究较少。且关于工况参数对轴承稳态润滑性能的影响也缺少全面系统的研究。本文作者基于数值分析方法，应用Matlab 软件对船舶可倾瓦推力轴承进行热弹流动压润滑理论分析，探讨工况参数对轴承润滑性能的影响，分析转速和载荷对推力轴承静动特性的影响，为轴承使用提供理论支撑。

1 热弹流动压润滑理论模型

1.1 稳态润滑特性计算模型

1.1.1 油膜厚度方程

可倾瓦推力轴承的物理模型如图1 所示。

图1 可倾瓦结构Fig.1 Tilting tile structure

图中：hp为支点油膜厚度；rp为支点半径；θp为支点周向角；γθ为支点周向倾角；γr为支点径向倾角；h为油膜厚度；r为径向位置；θ为周向位置。

油膜厚度方程为

1.1.2 雷诺方程

船舶可倾瓦推力轴承的热弹流动压润滑情况可用雷诺方程求解，柱坐标下的雷诺方程［12］为

式中：p为油膜压力；h为油膜厚度；μ为润滑油黏度；ω为工作转速。

1.1.3 能量方程

能量方程可以求解油膜温度分布，绝热状态下能量方程形式为

式中：Cp为润滑油的比热容；ρ为润滑油密度；T为油膜的温度。

1.1.4 黏温方程

润滑剂的动力黏度的经验公式［13］为

式中：λ为润滑剂的黏度指数；T0为进油口油温；μ0为T0下润滑剂动力黏度。

1.1.5 弹性变形方程

根据弹性半无限体理论，任意点受到压力时，会对其他点产生影响，积分后可以得到任意点的弹性变形［14］：

式中：E为轴瓦的弹性模量；P0（θP0，rP0）为特定点位置；pP0为特定点压力。

1.1.6 热变形方程

式中：αp为瓦块的热膨胀系数；B为轴瓦宽度；H为轴瓦厚度。

1.2 瞬态特性计算模型

1.2.1 瞬态雷诺方程

油膜的动态特性参数由油膜刚度和油膜阻尼表现，考虑时间因素的瞬态雷诺方程为

1.2.2 油膜厚度方程

推力轴承在工作时轴承的振动会引起油膜力发生变化，会造成油膜厚度的变化。由于推力轴承主要承受轴向载荷，只考虑轴向扰动所带来的变化。新的油膜厚度方程：

式中：h0为稳态油膜厚度；Δz为推力盘的轴向位移量。

1.2.3 油膜压力方程

扰动所造成的油膜厚度变化会引起油膜压力的变化，将油膜压力应用泰勒公式展开，取其线性向，油膜压力可表示为

式中：p0为稳态油膜压力；Δz·为油膜厚度的扰动。

1.2.4 油膜刚度和阻尼方程

将式（8）和式（9）代入式（7）中，可得到油膜刚度系数K和阻尼系数D求解方程。经过推导得到刚度系数和阻尼系数方程为

2 数值计算方法与流程

2.1 计算方法及收敛条件

对雷诺方程和能量方程量纲一化处理后，利用有限差分法对方程离散化处理，将推力轴承沿周向和径向方向进行网格划分，用差商形式表示，利用超松弛迭代法进行求解。

油膜压力和温度收敛条件如下：

2.2 计算流程

基于热弹流动压润滑理论，结合轴瓦的热弹性变形，利用Matlab 软件进行求解计算得到油膜厚度等润滑相关性能参数，计算流程如图2 所示。

图2 数值计算流程Fig.2 Numerical calculation flow

2.3 模型验证

为了验证上述模型的正确性，选取文献［12］中的数据进行验证，基本参数如表1 所示。

表1 推力轴承参数Table 1 Thrust bearing parameters

图3 所示为文献［12］得到的周向倾角0.003°时油膜压力随周向倾角的变化，图4 所示为周向倾角0.003°时最大油膜压力所在的径向截面图；图5、6所示分别为文中计算得到的油膜压力分布和油膜压力随径向倾角的变化。

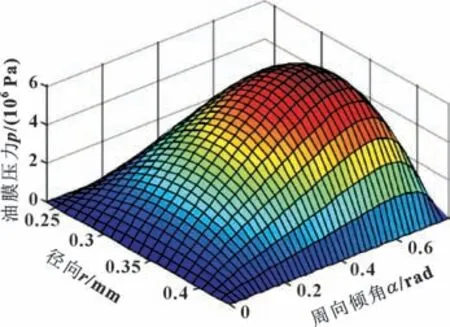
图3 文献［12］油膜压力分布Fig.3 Oil film thickness distribution in reference 12

图4 文献［12］油膜压力随径向倾角变化Fig.4 Variation of oil film pressure with radial inclination angle in reference 12

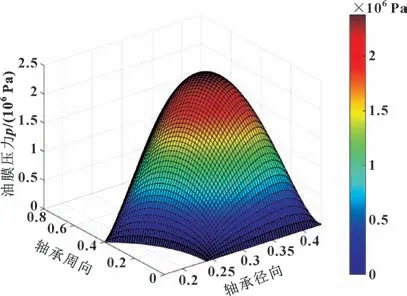
图5 文中油膜压力分布Fig.5 Oil film thickness distribution in this paper

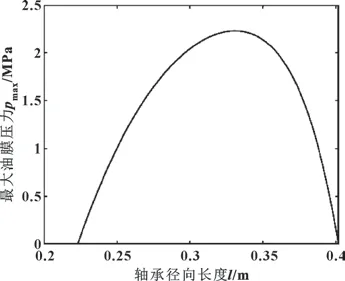
图6 文中油膜压力随径向倾角变化Fig.6 Variation of oil film pressure with radial inclination angle in this paper

通过对比可知，文中由于考虑了轴瓦的热弹性变形，导致油膜压力偏小，但油膜压力分布沿轴径向和周向方向上的变化趋势基本一致，可以证明文中热弹流润滑模型的正确性。

3 推力轴承润滑特性分析

文中计算并分析了不同载荷和转速条件下可倾瓦推力轴承润滑特性的变化规律。相关参数如表2 所示。

表2 推力轴承参数Table 2 Thrust bearing parameters

3.1 可倾瓦推力轴承润滑性能分析

在转速为600 r／min 的工况条件下，按表2 中轴承参数通过计算得到油膜厚度、油膜压力和油膜温度分布，如图7—10 所示。如图7 所示，油膜厚度从润滑油进油端口向出油端逐渐减小，且最小油膜厚度出现在出油端；油膜厚度沿周向方向变化较大，沿径向变化不明显。如图8、9 所示，油膜压力分布比较均匀，油膜压力的峰值靠近轴瓦的出油端。如图10 所示，油膜温度沿周向方向逐渐增大，从轴瓦的进油端到出油端油膜温度有明显的上升；油膜温度沿径向方向变化不明显，油膜温度的最大值出现在轴瓦出油端。

图7 油膜厚度分布Fig.7 Oil film thickness distribution

图8 三维油膜压力分布Fig.8 Three－dimensional oil film pressure distribution

图9 二维油膜压力分布Fig.9 Two－dimensional oil film pressure distribution

图10 油膜温度分布Fig.10 Oil film temperature distribution

3.2 载荷对推力轴承润滑特性的影响

在转速均为600 r／min 时，分析了轴承单瓦载荷在4、6、8、10、12 kN 下的推力轴承润滑特性变化规律。

3.2.1 载荷对推力轴承稳态特性的影响

图11—13 示出了不同载荷下最小油膜厚度、最大油膜压力、最大油膜温度变化曲线。随着载荷的不断增大，最小油膜厚度明显减小，而最大油膜压力和最高温度增加。这是因为在转速不发生变化时，载荷对油膜压力有直接影响。随着载荷的增大，不利于轴承形成良好的润滑条件，直接影响油膜的形成，且局部区域压力过大导致油膜厚度减小，油膜厚度变化影响油膜温度的变化；油膜厚度减小即进油量减小，导致摩擦热量增大从而使油膜温度上升，与实际推力轴承润滑理论相符。当载荷增大时，油膜厚度减小，从而使轴承的润滑能力下降，因此要特别注意重载情况下轴承的润滑状况。

图11 最小油膜厚度随载荷变化Fig.11 Variation of minimum oil film thickness with load

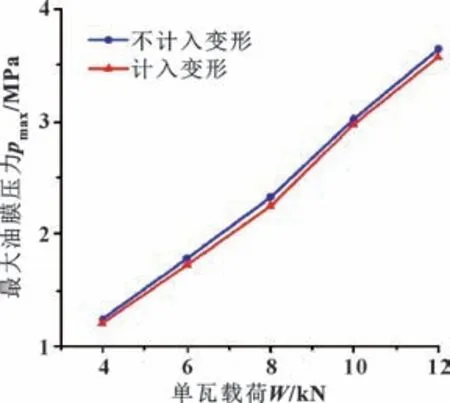
图12 最大油膜压力随载荷变化Fig.12 Variation of maximum oil film pressure with load

图13 最高油膜温度随载荷变化Fig.13 Variation of the highest oil film temperature with load

考虑热弹性变形时，最小油膜厚度大于不计入变形时，而最大油膜压力和最高温度都比不计入变形时要低，说明在正常工况条件下，适宜的轴瓦变形能够有效地改善轴承的润滑性能。

3.2.2 载荷对推力轴承瞬态特性的影响

图14、15 给出了油膜刚度和油膜阻尼随载荷的变化曲线。随着载荷的增大，油膜的刚度和阻尼不断增大。这是因为载荷的增大导致油膜厚度减小，而油膜刚度和阻尼跟油膜厚度成反比。在载荷相同的情况下，考虑热弹性变形时轴向刚度和阻尼比不计入变形时要低；当载荷较大时，计入变形时油膜刚度和油膜阻尼增大幅度明显下降。这是由于载荷较大时，轴瓦的热弹性变形更加明显，对油膜的刚度和阻尼影响加剧。

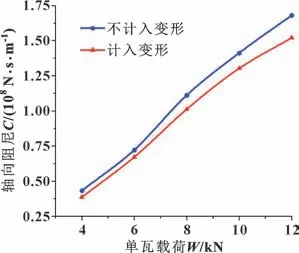
图15 轴向阻尼随载荷变化Fig.15 Variation of axial damping with load

3.3 转速对推力轴承润滑特性的影响

在单瓦载荷均为10 kN，轴承转速分别为200、400、600、800、1 000 r／min 时，分析转速对轴承润滑性能的影响。

3.3.1 转速对推力轴承稳态特性的影响

图16—18 所示为推力轴承稳态特性参数随转速的变化曲线。

图16 最小油膜厚度随转速变化Fig.16 Variation of minimum oil film thickness with rotational speed

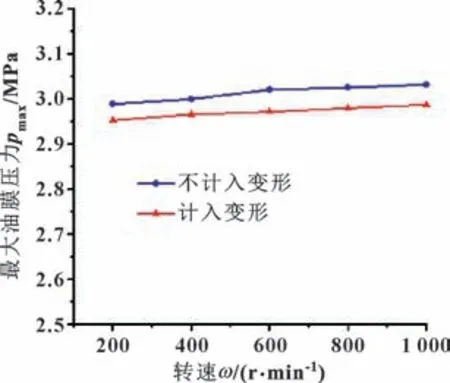
图17 最大油膜压力随转速变化Fig.17 Variation of maximum oil film pressure with rotational speed

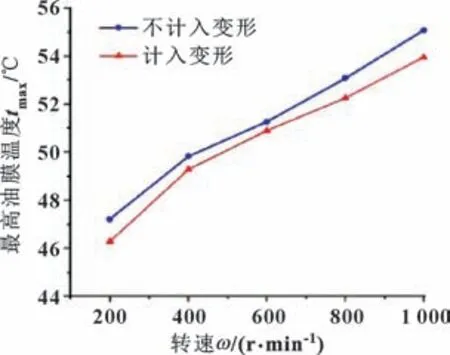
图18 最高油膜温度随载荷变化Fig.18 Variation of the highest oil film temperature with rotation speed

随着速度的增大，最小油膜厚度有明显的提升，且增幅较大。转速的增大有利于形成良好的动压润滑情况，而最大油膜压力基本不发生变化，这是因为油膜压力主要取决于载荷的大小，在相同载荷的情况下，油膜压力变化不明显，这也说明压力对转速的变化不敏感。随着转速的增大，轴承的最高油膜温度明显升高。说明在高速工况下，尽管转速会让进油流量增大使油膜厚度提高，从而使油膜温度降低，但由于转速的增加油膜的剪切率也会增加，使剪切损耗增大，导致轴承的温度增高。

计入热弹性变形时，最小油膜厚度增大，最高油膜温度和最大油膜压力降低，但最大油膜压力的变化不明显。

3.3.2 转速对推力轴承瞬态特性的影响

图19、20 示出了不同转速下油膜刚度和油膜阻尼的变化曲线。随着转速的提高，油膜刚度和阻尼均减小，其中在较低转速范围时，油膜刚度和阻尼降幅更为明显。计入热弹性变形时油膜刚度和油膜阻尼相对较低。

图19 轴向刚度随转速变化Fig.19 Variation of axial stiffness with rotation speed

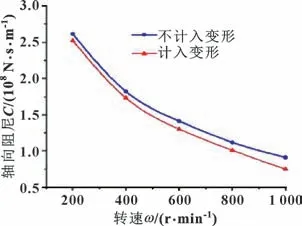
图20 轴向阻尼随载荷变化Fig.20 Variation of axial damping with rotation speed

4 结论

通过Matlab 软件建立热弹流动压润滑模型，考虑轴瓦热弹性变形，分析不同转速和载荷条件下轴承润滑性能的变化规律。具体结论如下：

（1）在稳定工况下可倾瓦推力轴承的热弹性变形对润滑性能影响较大，轴瓦的热弹性变形有利于形成良好的动压润滑环境。

（2）在转速相同时，随着载荷的增加，最小油膜厚度减小，最大油膜压力和最高油膜温度增大，轴承的润滑性能明显下降。随着载荷的增大，油膜的刚度和阻尼不断增大，当载荷较大时，计入变形时油膜刚度和油膜阻尼增大幅度明显下降。

（3）在载荷相同时，随着转速的提高，油膜厚度和油膜温度呈线性变化。转速增加，最大油膜压力变化不明显，油膜刚度和阻尼呈减小趋势，在低速区降幅更明显。计入热弹性变形时油膜刚度和油膜阻尼相对较低。