基于影响线跑车加载的桥梁承载力快速评估方法

南 鹏

（江门市新会区公路发展有限公司,广东 江门 529000）

0 引言

传统桥梁承载力试验时，道路必须被封锁，并且需要技术人员指导和安排测试车辆，测试流程烦琐，需要耗费大量人力和物力。而拟静态的影响线可以通过小型车辆以规定路径低速恒速行驶的方式获得[1]。小型车辆在桥梁上缓慢行驶，可以得到拟静态的影响线，其测量结果相对稳定。与传统的载荷测试相比，拟静态的影响线测试更加快捷、方便[2]。小型车辆可以用作轻型载荷，可用于新桥评估、老桥承载能力评估以及桥梁的承载能力评估。

1 工程概况

某公路桥梁，总长270.66 m，采用13 个跨度为20 m的跨径组合。桥宽为11.2 m，横向对称设置，分别为两侧0.5 m 护栏、两侧10.25 m 净宽桥面和中央1.5 m 隔离带[3]。该桥梁采用C40 简支RC T 型梁作为上盖，下盖为带肋板平台、柱式墩和桩基。该桥梁主要承受了汽-20 和悬挂-100 两种荷载，并于1993 年完工并投入使用。目前，该桥采用13 cm C40 水泥路面+7 cm 沥青路面进行路面铺设。该桥的5×20 mT 梁连接示意图如图1 所示。

图1 15×20 mT 梁连接示意图

2 轻荷载试验方法

该研究使用了拟静态效应试验机来进行试验。在一台试验机的受载条件下，对该桥进行了变形及变形影响试验。基于这些试验结果，来将其转化为常规加载实验中的加载效率和校正因子[4]。通过这种转化，确保了加载效率和校正因子在0.85～1.05 的范围内，并与现有的相关标准相一致。这使得能够快速评定新桥和老桥在线性弹塑性状态下的承载力。

校验系数是评价桥梁承载力的一项关键参数，其数学公式为：

式中，Se——试验荷载状态下的弹性位移值和弹性挠度值；Ss——试验荷载状态下的结构位移值和结构挠度值。

将公式（2）代入公式（1），可以得到校验系数的刚度数学表达式（3）：

式中，M——桥梁荷载对任意断面的弯矩；y——这一位置至断面中轴线的长度；EI——横梁的抗弯刚度；EsIs——理论上的弯曲刚度；EeIe——实测位移对应抗弯刚度。

从式（2）和式（3）可以观察到，结构的位移校验系数在形式上可以通过位移值转化为刚度值，如图2所示。

图2 受集中力作用的简支梁

可以看出，当一个集中力被施加于一个简单的梁体时，根据结构力学，可以得出一个简单的挠曲方程式（4）：

将式（4）代入式（1），得到挠度校验系数也由刚度定义，其计算公式如下：

从桥梁变形的角度来考虑，可以将变形量转化为刚性量。同样地，也可以用相应的弯曲刚度与相应的弯曲刚度之比来确定偏移校正因子。在线性弹性下，校验系数与其刚度相关。校验系数为一个常数，不依赖于加载车的自重和位置。然而，在对桥梁进行载荷实验时，分期加载是一个外荷载逐渐增加的过程[5]。因此，可以得出结论：在每个载荷加载条件下，加载效率与校验系数之间存在一定的函数关系；在重荷载与轻荷载下，校验系数之间也存在一定的函数关系。这样，就可以根据轻型荷载的荷载效应，得到重型荷载作用下的结构检验因子。在此基础上，将其与相关标准相结合，可以对其进行综合评价[6]。因此，在分析函数关系时，设定轻度荷载的荷载效率设定为小于0.84，并分为五个区间，分别是0.75～0.84、0.65～0.74、0.55～0.64、0.45～0.54、0.3～0.44。同时设定重度荷载的荷载效率为≥0.84。然后通过作差的方式对重载荷和所划分的轻载荷下的校验系数进行了计算，进而得出公式（6）和公式（7）：

式中，Δa——绝对差值；ζ——重荷载状态下的校验系数（包括位移校验系数和挠度校验系数）；ζn——轻荷载状态下的校验系数（包括位移校验系数和挠度校验系数），n=1～5；Δr——相对差值。

采用四分位方法，对计算出的每一座桥梁在不同载荷效率下的结构变形（或挠度）校正因子差异进行分析，得出校正因子差异的幅度并构建其与其相应的载荷效率之间的关系式。结合组合差异的幅度，结合公式（6）、（7）等，能够计算出在重荷载下的校验系数。Δr-η校正回归方程如表1、2 所示。

表1 钢筋混凝土梁桥位移校验系数差值范围

表2 钢筋混凝土梁桥挠度校验系数差值范围

3 基于影响线跑车加载的桥梁承载力评估

3.1 试验工况

影响线试验分两种工况进行。

工况1：试验车辆以小于5 km/h 的恒速行驶，在桥面间距为2.4 m 的位置进行试验，并对试验车辆进行验证。测试车辆的轴距为1.45 m、轴重为9.94 t。

工况2：试验车辆以小于5 km/h 的恒速行驶，在桥面间距为4.2 m 的位置进行试验，并持续收集和记录数据。测试车辆的轴距为4.10 m、轴重为13.46 t[7]。

具体影响线试验布置如图3～5 所示。

图3 影响线测试工况横断面（m）

图4 影响线测试工况平面布置（m）

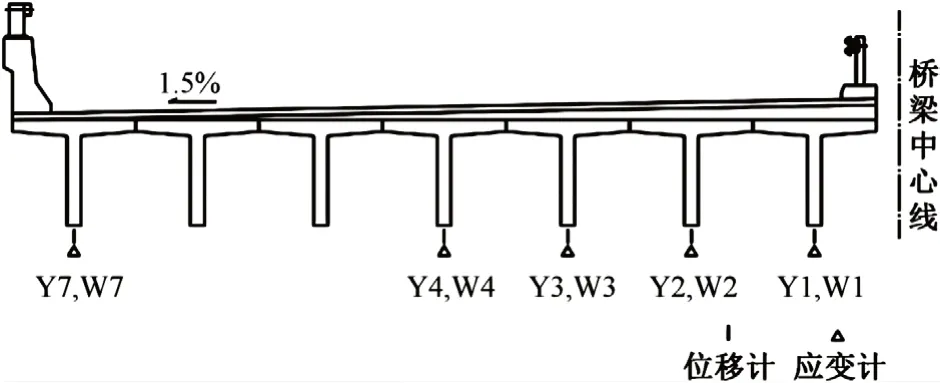
图5 跨中截面挠度与位移测点（m）

3.2 承载力评估

在进行加载后，影响线测试仪会对每个测点处的变形量进行汇总。按照载荷试验规范，采用整个跨段断面的变形量来进行加载[8]。从而得出了在影响工况1、2 状态下的加载效果，见表3。

表3 轻荷载试验荷载效率系数

根据表格3 所示，可以得出工况1 和工况2 状态下的偏转轻载系数为0.3～0.84。可以采用线性回归公式进行推算。根据该桥梁的1 号、2 号、3 号、4 号和7 号测点的理论值和实测值，能够计算出在轻荷载状态下的位移校验系数和挠度校验系数。进而可以根据两个校验系数的回归公式，将轻荷载校验系数转化为重荷载效率（在0.85～1.05 区间内）的校验系数，具体数据如表4 所示。

表4 轻荷载校验系数转变为重荷载校验系数数据

统计轻荷载与重荷载校验系数各自的分布范围，得出的结论见表5 和表6。

表5 位移校验系数分布范围

表6 挠度校验系数分布范围

从表4～6 可以看出，轻荷载下的校正因子变为重荷载下的校正因子后，各个测点的位移校正因子均小于1，而3、4 测点的位移校正因子却大于1，这表明整个大桥处于一种弹性工作状态，其承载力未达到设计标准。

4 结语

综上所述，该文基于某公路的桥梁工程，提出基于影响线跑车加载的桥梁承载力快速评估方法，并设置两种工况的影响线跑车加载试验，试验快速、准确地检测出该桥梁处于一种弹性工作状态，其承载力未达到设计标准。由此可以看出，该文提出方法能够代替传统检测方法，节省大量人力物力，有效提高桥梁承载力检测效率。