基于道路设计和交通规划的道路路线优化研究

施舒海

（中国市政工程中南设计研究总院有限公司,湖北 武汉 430000）

0 引言

道路工程作为社会经济发展的重要控制因素，能够加强区域连接、促进区域系统发展、提高民众生活质量，在我国社会建设中具有举足轻重的作用[1-2]。同时随着城市化进程的不断发展，为满足城市民众的生产生活需求使得道路建设、改造项目激增[3]。道路设计的主要工作内容是根据地形地貌、工程地质条件和水文地质条件等寻找能够满足设计、交通规划、环境和社会限制条件下的三维线路走向[4]。三维道路路线设计的原理是将二维水平和垂直路线在空间中进行叠加，基于此设计原理该文中将三维对齐视为一个双目标问题，利用帕斯托优化模型对线形设计方案进行优化，并在以往优化设计模型的基础上扩展了关于道路路线设计和成本计算方式的细节，能够在满足道路设计和交通规划的前提下对道路工程线形设计方案进行优化。

1 道路线形优化模型要点

1.1 水平线形

在该文的所述优化模型中，道路工程水平线形由切线段和圆曲线组成。水平线形的几何形状需要满足两个标准：①走线应满足指定的方向，例如切线—圆弧—切线；②走线的第一段和最后一段应为切线段。环形曲线位于两个相邻切线之间，以减轻路线方向的突然变化，这也是道路设计的标准。

水平线的几何设计由一系列交点位置和圆曲线r的半径进行描述[5]，每个交叉点都有三个相关的决策变量，即x、y、r。因此，道路工程线形设计的起点和终点坐标分别为：起点S（xs，ys，zs），终点E（xe，ye，ze）。在水平线形设计中，起点、终点坐标可简化为：起点Sh（xs，ys），终点Eh（xe，ye）。道路曲线段和直线段连接点的坐标为：（p1，p2，…，pn），则对应的曲线段半径合集为：{r1，r2，…，rn}。

如图1 所示，在道路水平线形设计中，可插入N+1个切线路段和N个圆曲线段，从而得到精确的水平线形。

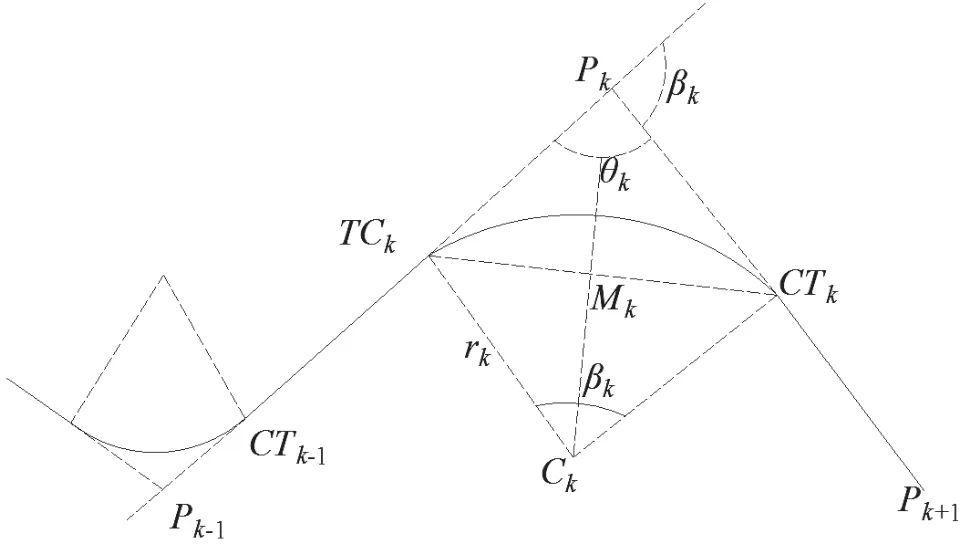
图1 水平对齐几何图形

过渡点TCk、CTk的计算如下：

给定连接点pk-1、pk、pk+1，以及圆弧段半径rk，则

定义Lk为从Pk到TCk的距离：

式中，Lk——圆弧的中心角（°），如图2 所示。

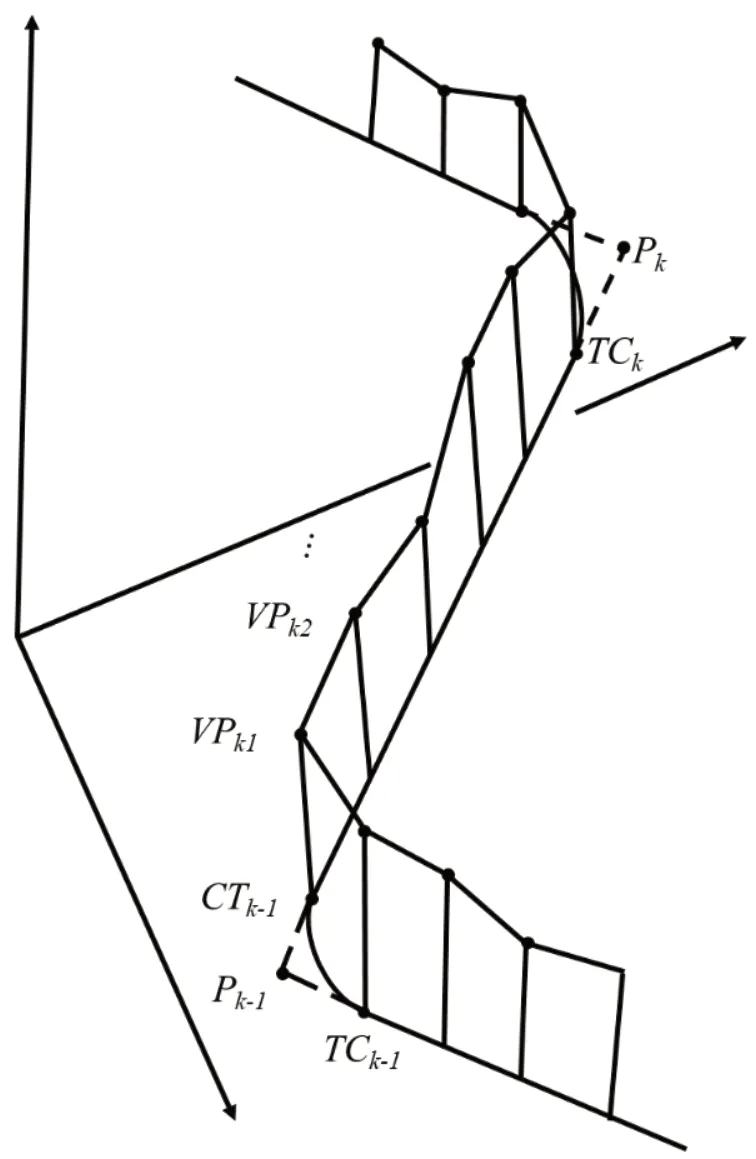
图2 3D 道路路线示意图

式中：

则有：

则有线形交界点可表示为：

1.2 垂直线形

垂直线的几何设计规定了道路上某一点的标高。在该文所述模型中，由称为垂直切线的直线组成。在模型开始时，沿水平线拉伸一个与x-y平面正交的平面。拉平后的表面称为h-z平面，其中h是沿水平线测量的距离。三维道路线形在h-z平面上的投影就是纵向线形。

图2 为3D 道路路线示意图，将CTk1和TCk之间的水平切线划分为mk个等距点，以此为节点，定义垂直点位：

式中，VPkj——图2 中等距点坐标，可表示为（xk,j，yk,j，zk,j）。

道路交叉设计标高（xk,j，yk,j，zk,j）的数学表达如下：

则线形任意点的坐标可计算为：

2 优化方法研究

多目标优化（MOO）（也称为多标准优化或矢量优化）可定义为寻找决策变量矢量的问题，该矢量既要满足约束条件，又要优化目标函数矢量，双目标优化指的是向量包含两个目标函数的特定情况。通常情况下，不存在对所有目标同时最优的唯一解决方案，因此只能考虑目标之间的权衡，而多目标优化的主要目标就是寻求最佳权衡，以支持决策者选择最终的首选方案。虽然对于多目标决策问题没有公认的解决方案概念，但一个好的解决方案一定不会被其他可行的替代方案所支配，非支配点集合被称为Pareto 最优集合。

在道路线形设计过程中，工程师可能需要实现不同的目标，包括建设成本、施工难度、交通规划设计等。其中工程建设成本需要道路线形尽可能简单且土方开挖数量较少、工程地质与水文地质条件可能会导致线形适当增加，道路工程整体规划会要求道路线形长度增加等。为综合考虑道路线形设计，平衡各方面因素关系，该文基于上述三维道路线形设计方法将线形优化问题考虑为一个双目标优化问题。

给定的控制域内控制决策变量，构建约束组合，在约束组合的条件下是的多个目标趋于最优化，多目标问题可描述为：

式中，x=[x1，x2，…，xm]——m个决策变量；F(x)——优化目标；hi(x)、gi(x)——约束条件。

在决策空间S中的决策变量，对于任意条件下的i∈{1，2，…，v}，满足fi(a)小于fi(b)，则称变量a支配变量b。对于多目标优化问题中的一个可行解x，能够达到决策空间中不存在变量能够支配可行解x，则称x为Pareto 有效解。该研究对Pareto 多目标优化的排序方案进行了修改，根据方案在当前种群中的非支配水平和给定的偏好向量来评估方案的适应性。

3 案例分析

3.1 案例简介

某公路工程示意图如图3 所示，工程建设目的为扩展现有路网，缓解交通压力。道路全长3.251 km，道路工程为4 车道，限速40 km/h，规划路幅宽26 m，建设内容包括道路工程、排水及管线综合工程、交通设施工程、照明工程、绿化景观工程。该线路段原始地貌为构造剥蚀低山丘陵与山间冲沟区，整个线路地势起伏不大，但线路范围内存在河流及小山丘，山坡坡度约为17°，部分参数如表1 所示。如图3 所示，共有四条备选方案，其中方案1 为借助现有路网达到链接起点与终点的作用，方案2、3、4 均为新建道路。

表1 主要指标表

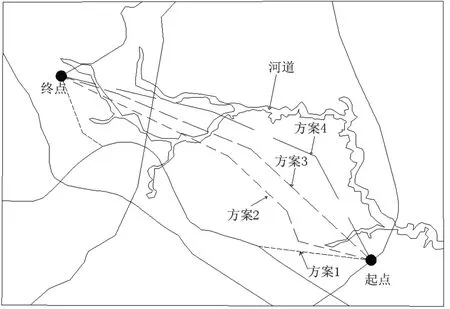
图3 道路工程示意图

3.2 优化结果分析

由于研究区域相对较小，并且新路线的端点是固定的，因此可以合理地预期新的交通规划要求和工程造价等对各种路线备选方案进行优化。为了更清楚地可视化线路优化设计方案，指定了以下两个优化目标，并使用方程进行测量：最大限度地降低公路建设的总成本，尽量缓解区域交通压力。

后处理程序进一步缩小了非主导解集的规模，从而可以更清晰地显示所获得的Pareto 前沿的轮廓，并合理限制向决策者提供的候选替代方案的数量。如图4 所示为后处理后的Pareto 排列，如图4 所示，方案3 中得到的Pareto 前线优于方案4 中得到的Pareto 前线，因为方案3 中的非主导解位于外层，这通常意味着得到的Pareto前线更接近真正的Pareto 前线。

图4 方案3、方案4 后处理后的Pareto 排列

与其他备选方案相比，方案1 由于借用了现状道路，虽然一定程度上缓解了起始点交通压力，但并未达到交通规划的要求，河道附近仍存在大面积未通路地区，对环境和社会经济领域的改善最小；方案4 对环境和社会经济领域的改善最大，但一定程度上增加了线路长度，进而导致项目预算增加；备选方案2 和方案3 是两个既定目标之间最佳折中的中间结果。方案3 是折中考虑方案2 和方案4 的方案，如果使用给定的偏好信息（w1=0.7，w2=0.3），采用加权汇总法进行评估，则备选方案3 是后处理Pareto 集合中的最佳解决方案。

4 结论

为进一步提高道路设计质量，该文对基于道路设计和交通规划设计的道路线形选择优化模型展开了系统的研究，所的主要结论如下：

（1）从三维道路线形设计机理入手，研究了道路线形设计基本思路，并在此基础上结合Pareto 多目标优化方法研究了基于道路设计和交通规划设计的道路线形优化选择模型，并给出了该模型的道路线形设计基础和多目标优化方法。

（2）通过对实际算例的分析，进一步论证了所建立的综合考虑道路设计和交通规划设计的道路线形优化模型具有一定适用性。该文研究内容对于后续道路线形设计优化工作的开展具有一定指导意义。