基于理论力学和计算机模拟的摆动螺丝研究

王梓豪,卞艺杰

(东南大学 吴健雄学院,江苏 南京 211189)

本文旨在通过理论力学中的运动学、动力学方程和计算机模拟研究螺丝在斜面上下滑时产生的振荡,并且研究与螺丝振荡摆角相关的参数.

1 问题重述

此问题来源于2023年国际青年物理学家锦标赛(IYPT)课题之一:在斜面上侧放一个螺丝并释放时,螺丝会沿着斜面向下运动,在运动过程中,螺丝摆动振荡可能逐渐增大. 本文主要探究摆角曲线形态,经过前期文献检索,暂没有任何相关文献解释此问题.

2 物理建模

2.1 物理模型

基于实际情形以及物理事实,本文所建立的螺丝及其在斜面上的运动的数学物理模型如下.

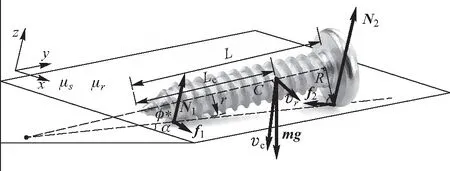
图1 螺丝受力分析图

首先,螺丝是一个匀质刚体且质量为m,并且由两部分组成,分别是螺杆以及螺帽. 螺杆部分是一个半径为r、高为L的细长圆柱体,螺帽部分是一个半径为R、高为h的扁平圆柱体. 螺丝的质心和螺丝根部之间的距离为Lc[1]. 螺丝的3个惯量主轴分别为螺丝的中心对称轴以及垂直于该中心对称轴的两个相互垂直的主轴. 根据模型的对称性,螺丝沿除中心对称轴外的两个惯量主轴的转动惯量相等,均为I1. 螺丝沿中心对称轴的转动惯量为I3. 螺丝在被放置到斜面上时和斜面之间共有两个接触点,分别位于螺丝根部和螺帽上,即螺杆圆柱体以及螺帽圆柱体的底面的边缘上,这两个接触点与斜面之间存在摩擦力,且两个接触点与斜面之间的滑动摩擦系数分别为μ1、μ2.

螺丝在斜面上运动时的受力情况较为简单,本文将螺丝所受的力正交分解到垂直斜面(z轴)以及沿斜面(x轴)两个方向上. 螺丝所受的外力有:

1) 螺丝所受的重力mg,等效作用点在螺丝质心上,方向垂直地面向下,可以分解为平行斜面向下的mgsinα以及垂直斜面向下的mgcosα,其中α为斜面倾斜的角度;

2) 螺丝所受的斜面的支持力N1、N2,作用点分别位于螺丝和斜面的两个接触点上,方向均垂直斜面向上,由于螺丝在垂直斜面方向上处于平衡状态,所以螺丝与斜面之间两个接触点处的支持力和重力在这一方向上的分量达到三力平衡,总体上来看既不产生合力,又不产生力矩,同时通过三者相互平行的性质也能够推出

(1)

(2)

其中l1、l2分别是质心到两个支持力的距离,根据几何关系可得

(3)

(4)

3) 螺丝所受的斜面的摩擦力f1、f2,作用点分别位于螺丝和斜面的两个接触点上,在摩擦力表现为滑动摩擦时,方向与接触点相对于斜面的速度方向相反;在摩擦力表现为静摩擦时方向不能通过力学系统的状态简单确定[1],但本文重点研究的是螺丝下滑中产生的越来越大的振荡,几乎不涉及对瞬态静摩擦力的讨论分析,所以为了简化问题,在之后的分析中会尽可能避免对静摩擦力的讨论,在没有特殊说明时,后文所说的摩擦力均指的是滑动摩擦力.

2.2 运动建模

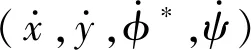
螺丝绕质心的定点转动可以通过欧拉运动学方程以及欧拉动力学方程来描述[2],由于螺丝的章动角θ固定,并且螺丝具有一定的对称性(惯量主轴的转动惯量I1=I2),方程可以简化为

(5)

(6)

(7)

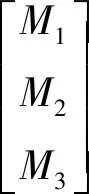
(8)

其中,固着坐标系的基坐标以及对应的由地面坐标系到固着坐标系的基变换矩阵可以通过三个欧拉角——进动角φ、章动角θ以及自转角ψ来表示.

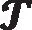
(9)

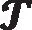
(10)

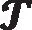
(11)

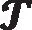
(12)

在地面坐标系下,对质心产生力矩的力只有螺丝与斜面之间的两个接触点处的摩擦力. 两处摩擦力的大小即为对应的动摩擦因数与正压力的乘积,它们的方向与接触点的速度方向相反. 接触点的速度可以通过螺丝根部速度以及螺丝角速度计算得出

(13)

(14)

其中,螺丝角速度为

(15)

螺丝根部到两个接触点的矢量为

(16)

(17)

得出两处摩擦力后,通过几何关系求出质心到两个接触点的矢量为

(18)

(19)

所以,地面坐标系的力矩即为

(20)

以上的讨论分析了螺丝绕质心定点转动部分,而螺丝质心的平动则可以通过质心运动定律来描述. 螺丝所受的合外力只有沿斜面向下的下滑力mgsinα以及两处摩擦力f1、f2,所以螺丝质心的运动方程为

(21)

其中,ac为质心加速度. 通过几何关系可得质心坐标为

(22)

对时间求二阶导数得

(23)

通过以上的分析,本文可以得到螺丝运动中的某一时刻的广义加速度与当前广义坐标、广义速度以及模型参数之间的方程关系,进而可以用作进一步的分析.

3 模拟实验

3.1 算法说明

本文基本算法流程如图2所示.

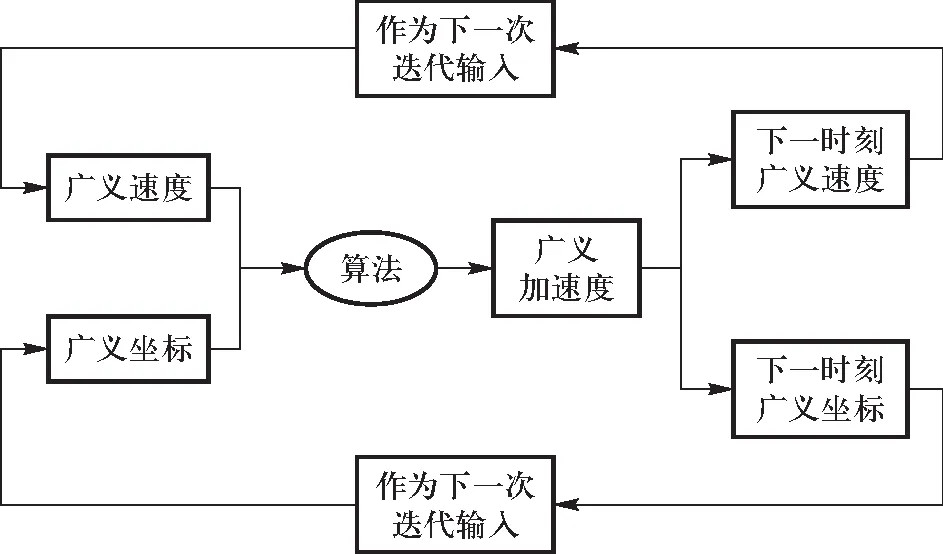
图2 算法流程图

结合上文的理论分析可知,对螺丝运动的模拟实际上是通过某一时刻的广义坐标以及广义速度求出广义加速度,再通过当前的广义速度求出下一时刻的广义坐标. 通过当前的广义加速度求出下一时刻的广义速度,如此反复迭代,便可由初始值求出之后任意时间步长的系统状态. 本文使用Δt以及N表示时间步长和步长数.

程序的关键初始参数如表1所示.

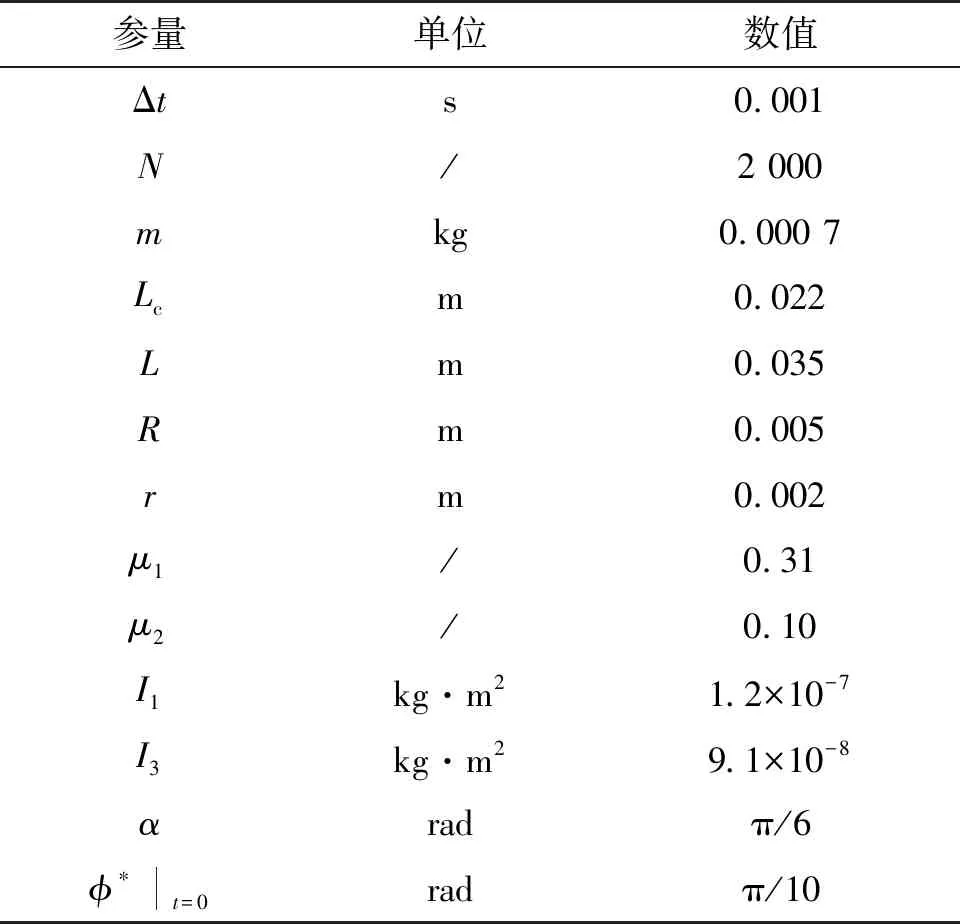
表1 程序关键初始参量

3.2 模拟结果

经过模拟得到的螺丝运动状态的数值解分别为图3、图4.

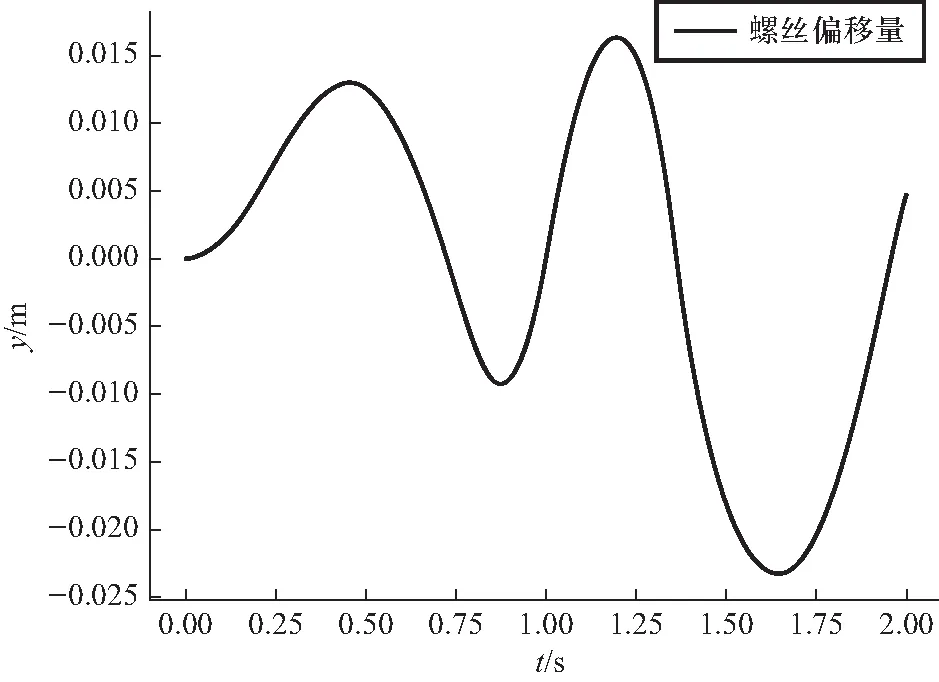
图3 螺丝y方向偏移量和时间的关系

观察图3,在模拟时间区间2 s内,螺丝的摆角首先从约20°的初始角度经过不到1 s的时间完成一个周期的摆动,达到反方向最大约30°摆角,随后向反方向摆动,摆过中轴线后摆角逐渐增大,最后在观察时间末尾增大到约60°. 在2 s完成了将近5/2个周期的摆动,与实际螺丝下滑情况符合较好.

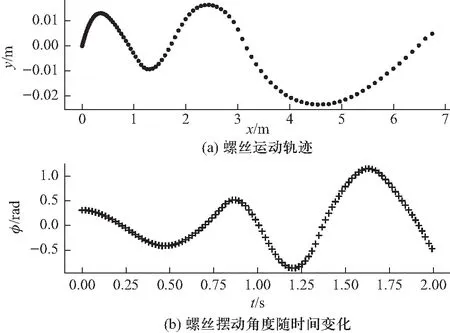
图4 螺丝运动状态图

观察图4上方子图,相邻两点间时间间隔为0.001 s. 随着时间的推移,螺丝合速度并非一直增大,螺丝并非沿着直线下滑,而是随着不规则的曲线下滑,并且偏移量较小.

观察图4下方子图,随着时间的推移,螺丝尾部y方向偏移也逐渐增大. 而且,螺丝y方向偏移量和螺丝摆动角度成负相关.

3.3 参数分析

本文首先研究初始摆动角度改变对螺丝摆动角的影响.

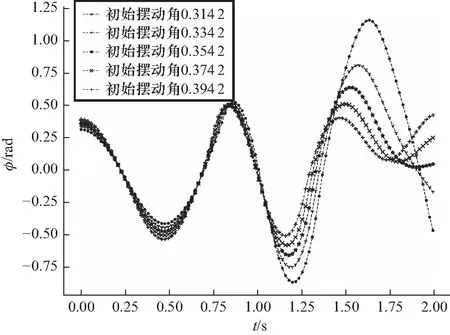
图5 初始摆动角改变下螺丝摆动角度和时间的关系

随着初始摆动角增大,2 s内的最大摆角、2 s内完成相同次数摆动所用时间逐渐减小,均成负相关关系. 曲线形态几乎相同. 更加值得注意的是,最大摆角并非随着时间增大,如图5中“+”线所示.

接着研究根部摩擦系数改变下摆动角与时间的关系.

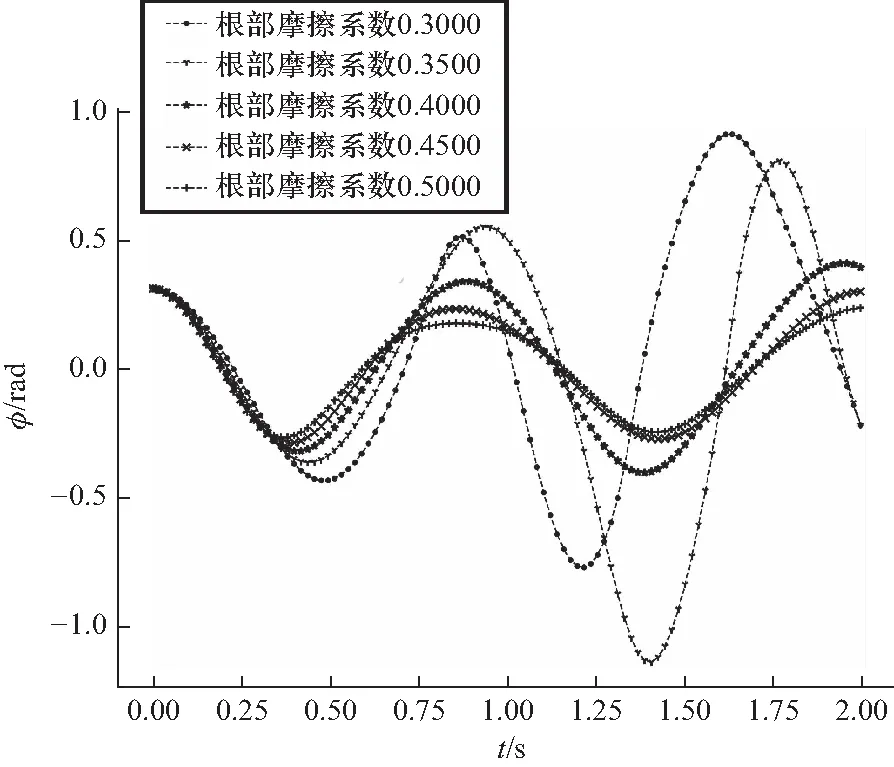
图6 根部摩擦系数改变下螺丝摆动角度和时间的关系

本文建立的模型对根部摩擦系数较为敏感,曲线形态统一度低. 2 s内最大摆角与根部摩擦系数的改变无明显正相关和负相关关系. 但是2 s内完成相同次数摆动所用的时长与根部摩擦系数的改变成正相关.

然后研究螺帽摩擦系数改变下摆动角与时间关系.

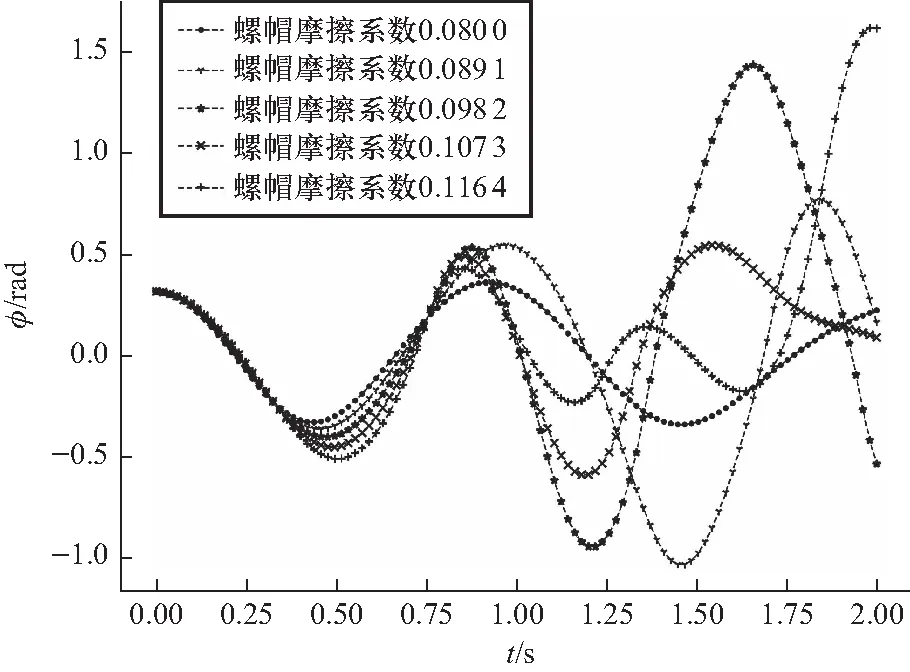
图7 螺帽摩擦系数改变下螺丝摆动角度和时间的关系

同样的,可以发现螺帽摩擦系数改变对曲线形态影响较大. 随着螺帽摩擦系数增大,2 s内最大摆角先增大后减小再增大. 更加值得关注的是,在某些螺帽摩擦系数下,最大摆角并非随着时间逐渐增大,比如图7中“+”线所示.

最后研究斜面倾角改变下摆动角与时间的关系.

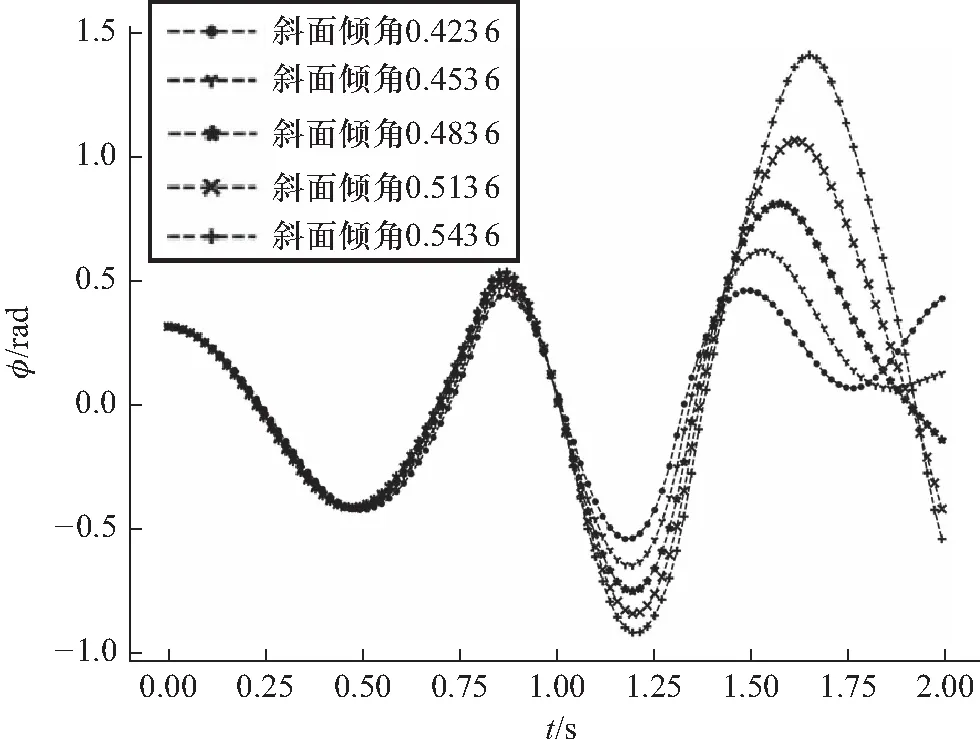
图8 斜面倾角改变下螺丝摆动角度和时间的关系

斜面角度从约24°改变到约31°,根据本文模拟,这是研究摆动螺丝比较适合的角度. 在斜面倾角增大的过程中,可以发现第一个周期的摆角极值差异微乎其微,但是在随后的第二个周期的摆动过程中差异增大,这种差异随着时间有累计效应. 2 s内最大摆角与斜面倾角成正相关. 2 s内完成相同次数摆动所用的时长与斜面倾角成负相关. 更加值得注意的是,斜面倾角的取值同样可能造成最大摆角并非随着时间逐渐增大,如图8中“·”线所示.

3.4 现象解释

对于初始摆动角,当初始摆动角增加时,又由于螺丝自旋主要由螺帽摩擦力矩驱动,因此螺丝自旋速度逐渐加快. 当螺丝自旋速度过大时,螺丝的摆动角就变得不易改变,因此出现最大摆角不随时间增大这一现象,这可以和高速旋转的陀螺不易倾倒作类比. 这一点同样可以用来解释斜面倾角增加,最大摆角不随时间增大的现象.

对于螺帽摩擦系数和根部摩擦系数,这两者更加直接地影响螺丝自转. 由于质心偏向于螺帽一侧,所以该侧支持力较螺丝根部支持力更大,而且螺帽半径大于根部半径,所以模型对螺帽摩擦系数比根部摩擦系数更加敏感.

3.5 经验公式

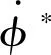
(24)

(25)

在vx与vy相差不很大时,有

(26)

以上过程可以表示为:

当T<0.5,

当T≥0.5,

T=nΔt

(27)

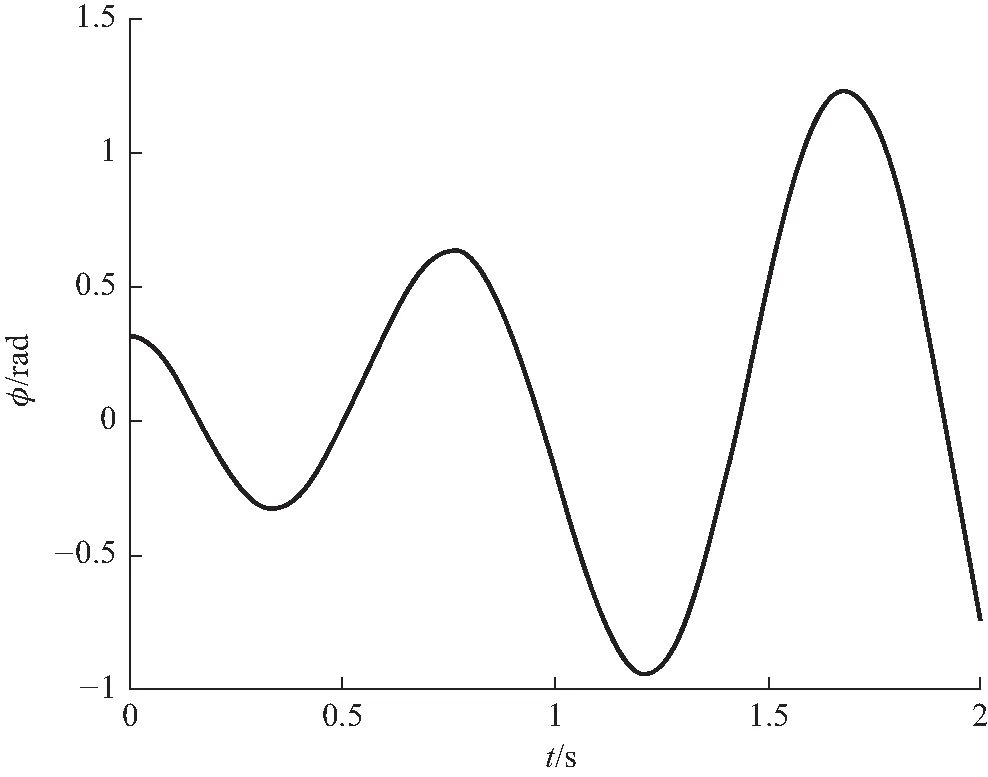
图9 经验公式图像

取κ1=9.4,κ2=0.14,κ3=7.2,κ4=1.3,m=1.1可得到图9,这与图8中“+”线非常相似.

4 总结分析

本文主要研究了摆动螺丝摆动角度随时间的变化规律,并且重点考虑了初始摆动角度、根部摩擦系数、螺帽摩擦系数和斜面倾角对摆角曲线的影响. 在表1的参数下,根据模拟结果,2 s内最大摆动角与初始摆角(20°左右)成负相关,与斜面倾角(28°左右)成正相关,与根部摩擦系数、螺帽摩擦系数既不正相关也不负相关. 以步长为0.01进行研究,模型对初始摆动角、斜面倾角、根部摩擦系数、螺帽摩擦系数敏感度依次增加. 主要研究初始摆动角、螺帽摩擦系数和斜面倾角会对最大摆角的影响是否随着时间而增大. 只改变其中一个参数,模拟得出2 s内能够使得螺丝最大摆角随时间增大的条件为:初始摆动角约为0.350 2 rad或螺帽摩擦系数约为0.108 4或斜面倾角约为0.498 6 rad.

本模型通过设置初始速度简化静摩擦力的影响,同时做到对真实实验的最大程度还原,可复现,可拓展性强,可用于其他相似系统. 本文提出了摆角曲线的经验公式,与模拟情况符合较好. 本模型仅研究了外界因素对摆动螺丝振荡曲线的影响,并未研究不同螺丝的摆动情况. 本模型还应进一步改进.

根据模拟情况,有几点需要说明. 第一,随着模拟时间增长,模拟结果混沌性增强,所以本文只研究2 s的变化. 这可能是由于迭代算法造成的误差累加. 第二,根据实际实验,并非所有螺丝摆角均随时间增大,有些类型的螺丝摆动规律混沌,多次实验结果可能完全不同,即实现摆角增大的实验条件较为苛刻. 根据模拟实验,实际实验需要特别注意根部摩擦系数与螺帽摩擦系数的选取,即平面材质的选取. 第三,经过多次实际实验发现,本模型适用于螺纹较密,长度适中的合金螺丝.