电流元观点下均匀磁化球体内部磁场问题的等效求解

曹修齐,邵瀚雍

(北京大学 信息科学技术学院,北京 100091)

在普通物理教学中,一个常见的问题是分析匀强磁场中的各向同性线性磁介质球体的磁化和磁感应强度分布. 该问题的求解一般需要对球体内部磁化产生的磁场进行微元积分,或更高阶的电动力学方法,存在一定教学难度.

该问题被描述为一个均匀磁化强度为M、半径为R的均匀介质球体内部磁化电流在球内任意一点的磁感应强度B. 在本文中将球心记为点O,需求解球中任一点A的磁感应强度B. 在该问题中,与磁化方向平行的球体中轴线的磁场强度可以利用其旋转不变的对称性质通过积分方法直接给出;但是对于其它位置的磁场强度则难以利用其对称性给出可解析求解的磁场强度积分表达式.

为此,较为常见的解法是在磁荷观点的视角下处理该问题,通过电荷分布对应静电场强度的已有结论和与之高度对称的假想磁荷,证明了球体内部的磁场强度始终为定值,则可在根据先前求得的中轴线结论外推出整个球体的磁场分布,即B=μ0H+μ0M求出全部位置的磁感应强度.

但是在实际的物理图像中,贡献磁场强度的并非磁荷而是磁化电流,因此完整的论证还应该包括对磁荷观点与电流元观点等价性的证明,这在极大程度上增加了完整求解的复杂度. 在国内外众多电磁学教材的相关讨论中均未严格讨论用磁荷观点代替电流元观点的可行性[1,2]. 本文力求在不超过普通物理的知识范围内简化论证过程.

本文通过割补和等效替代等物理手段,在符合物理图像的电流元观点下给出了简明严谨、易于理解的处理方法,在避免复杂数学运算的前提下实现了该问题的求解. 具体而言,在形式上虽然该问题与计算均匀极化球体内部一点的电场强度十分类似[3],但由于磁偶极子产生磁感应强度与电偶极子产生电场强度在偶极子所在位置是不同的,因而将球体分割成两个相对简单的部分,再叠加分割后的各部分产生磁场实现该问题的求解.

本文提出的等效替代求解方法严谨、简明的给出了类似物理问题求解新思路,对未来的普通物理教学有一定的参考价值和意义.

1 基于割补-替代思想的磁场求解

在本节中详细阐述了本文提出的等效求解方法的求解步骤和思路,应用较少的数学计算即可得到内部磁场磁感应强度的分布.

1.1 球体的分割

首先,如图1所示,考虑将球体分为2个部分. 分割出的第1部分为一个圆柱体,其高度远大于底面半径,中心对称点恰好为磁场待求解的A点,且圆柱的中轴线方向平行于磁化强度M的方向. 分割的另一部分为球体去掉该圆柱体的部分. 由于圆柱体的高远大于底面半径,根据安培定理,无限长圆柱体内磁场强度为定值,因此该部分的磁介质在A点产生的磁感应强度容易直接给出. 随后即可分别计算这两个部分在A点处产生的磁感应强度,具体过程见本文1.2与1.3部分.

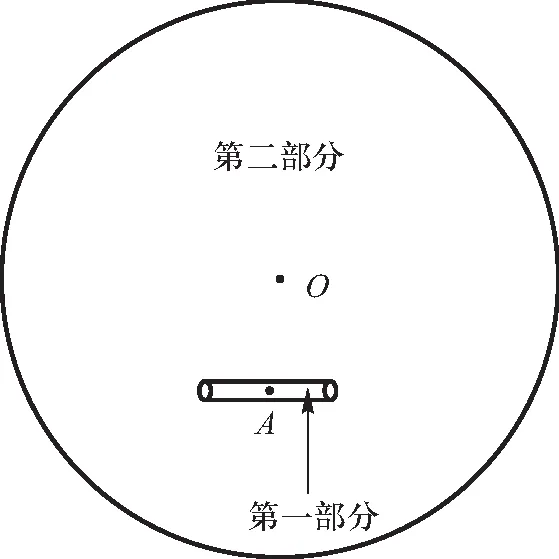
图1 球体分割示意图

1.2 第1部分对应磁感应强度的计算

第1部分可以看作是无限长且磁化强度矢量方向平行于中轴线方向的圆柱体在其轴线上产生磁场强度. 不妨假设在圆柱表面有均匀的磁化电流面密度i满足i=M,因此可将该部分等效为一个近似无限长均匀密绕直螺线管,通过安培环路定理可求出第1部分表面的磁化电流产生的磁感应强度B1为

(1)

在本部分的计算过程中,直接采用了基于电流元-磁感应强度的安培定理,这在普通物理的知识框架下也是易于理解的.

1.3 第2部分对应磁感应强度的计算

第2部分的计算主要包括2个步骤:1)对相同形状模型电荷分布产生的电场强度的计算;2)利用数学形式相似性进行等效的替代.

(2)

根据1.1中的分割假设,r远小于h,因此该部分产生的电场可以忽略不计. 我们只需考虑球体表面感应电荷在A点产生的电场:此时球体表面存在着面密度为σ=Pcosθ的感应电荷(其中θ为表面一点与极化强度矢量方向的夹角). 基于错位叠加法,不难推出式中的感应电荷面密度可以等效为2个球心距离ΔL、半径均为R的均匀带电球体O1与O2产生的电场强度,它们的电荷体密度分别为ρ与-ρ,且与距离满足ρΔL=P,如图2所示. 其中,O2O1方向为极化强度矢量的方向,O为O2O1中点.

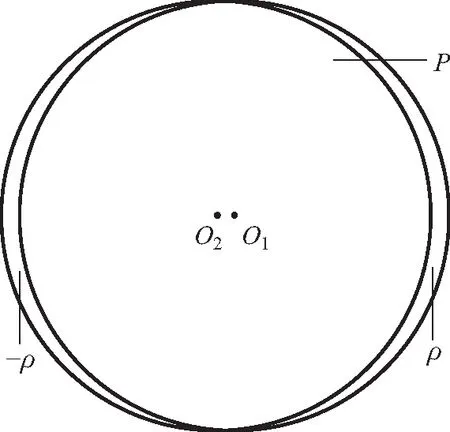
图2 第2部分的等效替代示意图

进一步的,A点的电场即为2个球体各种产生电场强度的矢量和,由高斯定理知以O1、O2分别为球心的球体在A点产生电场强度E1与E2分别为

(3)

因此,合场强E为

(4)

式中给出了电荷-电场模型下的电场强度与极化强度的关系. 为了将该结果推广到电流元-磁感应强度模型的结果,可以首先考虑两种模型在数学形式的相似性.

自由空间中电偶极子p=ql产生的空间电场分布可以直接表达为

(5)

环形电流对应的磁偶极矩m=iS在空间中产生的磁感应强度分布也可以表示为

(6)

(7)

在均匀极化的情况下Q=0,因此式中第一项为零. 类似的,磁矢势在远场近似后类似可以得出

(8)

与式(7)不同,因为不存在磁单极子,因此式中自然不存在第1项的结果.

根据式(5)、(6)易知,在数值上相同大小的电偶极子或环形电流(磁偶极子)所产生的电场/磁场的空间分布服从相同的函数. 而电极化强度矢量P的定义为单位体积的总电偶极矩,磁化强度矢量M的定义为单位体积的总磁偶极矩,因此P和M在物理意义上也可以做对称的变换.

(9)

在本部分的计算过程中,先利用已知的电荷-电场模型和错位叠加法求得了相似情况的电场强度,再直接由数学的相似替代法一步给出磁感应强度,避免了磁荷观点的论证.

值得补充的是,如果直接通过面磁化电流密度来处理图2的情况也可以求得类似的结果. 对于均匀极化P的介质球,极化电荷面密度为σ=Pcosθ,而均匀磁化M的介质球的面磁化电流密度j=Msinθ. 类似1.3中的错位方法,只需将错开的方向O1O2垂直于磁化强度M,即可将2个相同内部也存在均匀磁化电流的球等效为一个面磁化电流分布为j=Msinθ的球. 进一步利用电磁学中关于环形电流的中心垂直线磁场分布

(10)

或者通过对称的磁荷观点,也可以求出此时A点的磁感应强度.

1.4 两部分磁感应强度的叠加

综上所述,根据第1、2部分在A点的磁场叠加原理,可得到球内任一点A处的磁感应强度B为

(11)

上式即为问题所求的各向同性线性磁介质球体的磁化和磁感应强度分布.

2 方法分析与讨论

本文提出了割补-替代的物理手段,在电流元观点下简化了磁介质球内任一点磁场强度的求解过程. 根据割补法的物理思想,先将球体分为2部分,由叠加原理分别计算2部分产生的磁感应强度. 计算过程中,将两部分均转化为已知的模型进行处理,从而可以得到最终结果. 新方法相对于取微元再积分的方法体现了物理思维. 同时相对于教材上一般仅考虑中轴线的磁场情况更为全面与严谨.

值得指出的是,如果根据磁荷和电荷的对称性,可以直接将式(4)中求得的均匀极化电介质球内电场强度改写为均匀磁化磁介质球内磁场强度,但是这需要进一步严谨证明磁荷观点合理性. 而在本文中利用数学的形式替代手段改换变量,直接利用式(4)给出了对应的磁感应强度,通过较为简单的处理方法避免了引入磁荷的观点.

如果要使用ε-δ的数学分析语言来阐释这种方法也是容易推导的. 即对于任意的ε>0,可以取到适当的分割,使得第一部分产生的磁场与文中计算出的值的差小于ε/2,同时式(3)对应的磁场与文中计算的差小于ε/4. 然后取ΔL足够小使得第2部分产生的磁场与第2部分的等效替代模型的差小于ε/4,从而可以证明磁场与B的差值小于ε.

值得特别指出的是,本方法的核心创新点在于球体的分割假设,即一个r≪h、中心在A点、方向沿着磁化方向的圆柱体. 如果不满足此假设,比如取一个短而宽的圆柱、球体,或者A点不在圆柱的中心对称点,那么1.3中的讨论不再成立. 此时第2部分产生的磁场因为不满足r≪h的条件,式(2)不再成立,此时圆柱的顶、底面产生的磁场是有限量

而非零;同时第1部分产生的磁场也不满足无限长通电螺线管的中心假设,式(1)也不再成立. 因此只有在满足本方法假设的前提下才能同时处理式(1)、(2),这即为本文的核心方法. 该方法与静电场类似问题的解法比较接近,均使用到了等效模型的转化,但本方法使用了割补法和等效替代法,过程也更复杂. 因此该方法是对磁介质教材的有益补充.

本文提出的方法可以在较少数学计算的情况下解决一个经典问题,可以作为对部分教材中相关问题的有益补充. 同时结合了相关推导严谨证明了均匀磁化球体的内部磁场为匀强磁场,可以说明匀强磁场中的均匀磁介质球会均匀磁化的重要结论. 此外,本文处理物理问题应用的方法也可以用于教材上对学习者进行物理思维训练.