基于笔式鼠标和微晶导电板测绘静电场

曹彦鹏,张稚兰,包职刚,马巧云,周 严

(1. 天津商业大学 理学院,天津 300134;2. 天津商业大学 机械工程学院,天津 300134)

模拟法测绘静电场是高等院校大学物理电磁学部分的重要实验项目[1].传统实验中电极架采用双层式结构,上层放记录纸,下层放带电极的导电介质,通过移动双臂探针在记录纸上打出电势相等的点.然而实验中发现,移动同步探针寻找等位点效率低,操作步骤繁琐;过程涉及的数据处理量大且计算过程复杂,耗时较长.

现已有很多测绘静电场的实验方法,比如毕升、叶红军[2]利用Matlab软件模拟静电场的分布;郝艳玲[3]、章明[4]等人引入Origin软件处理实验数据并绘制电势图;也有许多文献对静电场描绘仪进行了改进[5-7].以上研究都侧重数据处理方法或仪器改进方面,都不同程度上减小了实验误差,提高了实验效率.但在实验的可操作性方面仍然需要改进,因此本文以微晶导电板作为电极之间的导电介质,利用带探针的笔式鼠标测绘静电场.实验中笔式鼠标直接在导电微晶板上探测等势点的位置,借助Geogebra软件(后文中用GGB代指)软件实时显示记录等势点的位置坐标,运用Origin软件拟合等势线、绘制二维等势线和三维等势面图.实践证明此方法提高了实验的可操作性,减小了数据的处理难度,提高了实验效率.同时,锻炼了学生的实践创新能力和科研能力.

1 测绘静电场实验的原理

1.1 用恒定电流场模拟静电场

静止电荷周围存在静电场,用实验方法直接测量电场是很困难的,利用稳态电流产生的静电场进行了静电场的模拟实验,稳定的电流场与静电场相似[8].导电介质中恒定电场和真空中静电场的电势都满足拉普拉斯方程,用同轴圆柱电极解释了静电场与电流场的相似性,分别利用静电场与电流场理论,推出静电场与电流场的势能分布规律的物理表达式,认为静电场和电流场的势能分布一致,因此通过测量和描绘恒定电流场中的电位分布来确定相应静电场中的电势及场强分布.

探针与笔式鼠标巧妙结合代替人工打点,利用GGB采集数据并拟合图线,最后用Origin完成数据处理并绘出图像,结果更加直观.双层电极架改为单层并用笔式鼠标代替传统探针,将复杂的仪器精简化也让操作更加高效,仪器轻便省时省力,因此相较传统实验更具推广价值和实用潜力.

1.2 真空中同轴电缆静电场分布

图1显示为同轴电缆和静电场的分布情况,在真空中存在半径为ra的长圆柱形导体A和内半径为rb的长圆柱形导体B同轴排列,分别带等量的异号电荷.从高斯定理可知,与轴线垂直的任一截面S中,均具均匀排列的辐射状电场线,不依赖于坐标z的二维场.二维场中的电场强度E与xy平面平行,它的等势面是一簇同轴圆柱面.所以只需对S面上的电场分布进行研究.

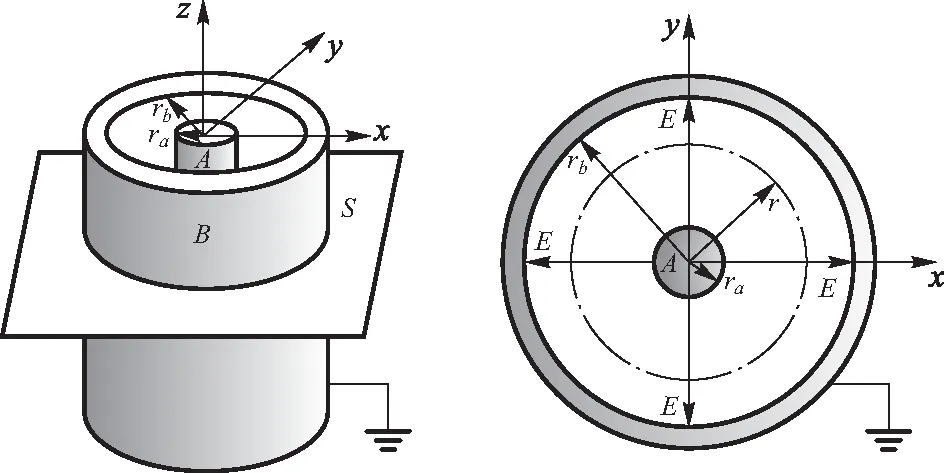
图1 同轴电缆电极模型及S截面静电场分布

由高斯定理,在离轴线距离r的电场强度为

E=λ/2πε0r

(1)

式中,λ为柱面单位长度的电荷量,其电势为

(2)

设r=rb时,Ub=0,则有

(3)

代入上式,得

(4)

可知,电流场中某点电势值Ur与该点所在等势圆半径r的对数lnr成正比.

2 实验原理

2.1 实验仪器

本实验仪器主要由稳压电源、静电场描绘仪、含探针的笔式鼠标、电压表、导线和笔记本电脑组成. 电源电压输出范围为7.00～13.00 V,分辨率为0.01 V,带2种电极(同轴电极、聚焦电极)的静电场描绘仪,如图2所示.含探针的笔式鼠标,可通过USB接口与电脑无线连接,如图3所示.安装GGB软件的笔记本电脑可实时显示探针的位置坐标.实验仪器整体布局如图4所示.

同轴圆柱电极的实验电路图如图4所示,电源输出电压给同轴圆柱极板的正负电极,电极间有导电率远小于电极且各向均匀的导电微晶,电子在电场作用下作定向运动形成径向电流,从而在导电微晶中形成恒定电流场.电压表一端与同轴圆柱外电极(负极)相连,另一端和金属探针相连,用来测量金属探针与负极板间的电压数值,带金属探针的鼠标可在同轴圆柱内、外电极之间自由移动探测电压,电压表实时显示各点电压数值,鼠标金属探针的位置坐标可在GGB软件中同步实时显示,当探测到目标电压时,按压笔身附带的位置确定键,即可在GGB软件中准确记录下探针所对应的等势点位置坐标.利用笔式鼠标的定位功能直接在导电微晶板所在的平面探测并记录等势点的位置,消除了传统实验中采用双层电极架探测和记录等势点在空间上的分离,借助鼠标灵活的移动,也使探测等势点更加便捷.

图2 实验仪器

图3 笔式鼠标

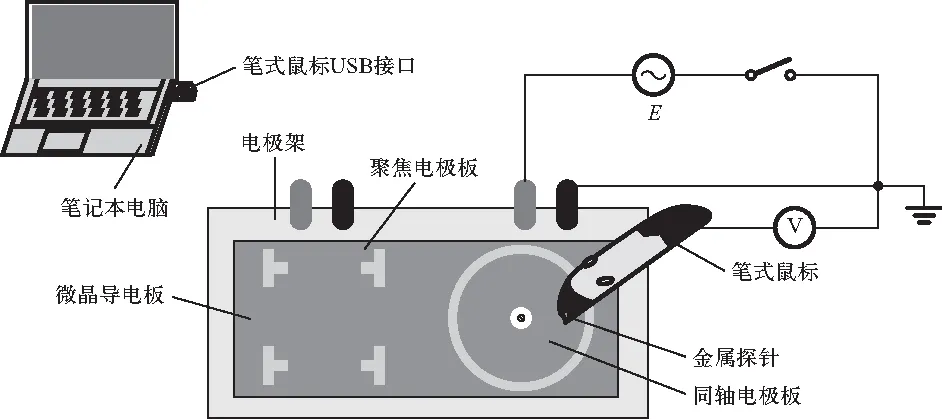
图4 实验仪器整体布局

2.2 实验操作流程

1) 按图2所示连接好电路;

2) 调节稳压电源输出电压为10 V;

3) 移动鼠标探针依次探测电压数值为2.0 V、4.0 V、6.0 V、8.0 V的等势点,同步在GGB软件中记录等势点的位置坐标,每条等势线上的8个点要求均匀分布;

4) 在GGB软件中利用“圆形拟合”得到等势圆,再用“向量”工具可垂直于等势线绘制出电场线.同理利用GGB软件也可绘制出相对复杂的聚焦电极的等势线和电场线,聚焦电极电路图如图5所示, 实验操作流程如图6所示.

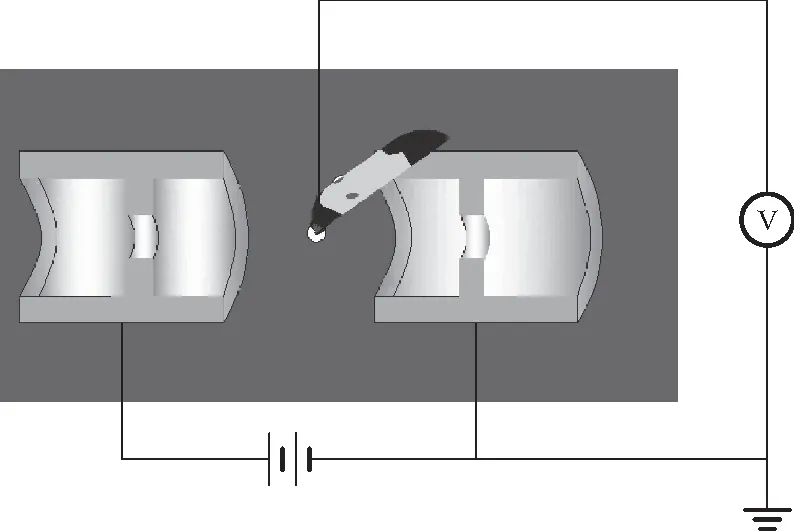
图5 聚焦电场电极电路图

图6 操作原理图

3 实验数据采集及处理分析

3.1 GGB软件数据采集

利用GGB中默认的二维直角坐标系,追踪探针位移并在相应位置按下确定键记录等势点,等势点坐标同步呈现在软件中,连接形成等势线进而画出电场线如图7所示.通过代数区记录打点的坐标数据如表1所示.

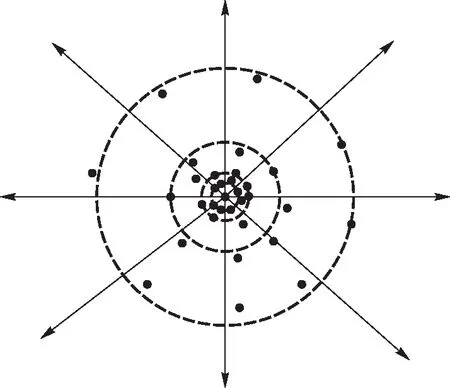
图7 利用GGB绘制同轴电极电场线

表1 实验同轴电极坐标数据(部分数据)

根据公式计算出各等势点的r值

(5)

依次求出笔式鼠标实验中各等势线半径平均值及对数值,如表2所示. 为与本实验比较,维持微晶导电板两电极间电压不变,采用传统实验双层电极架,移动双臂探针在坐标纸上记录各等势点的位置,然后手工绘制各条等势线后测量计算各等势线半径的平均值及对数值,如表3所示.

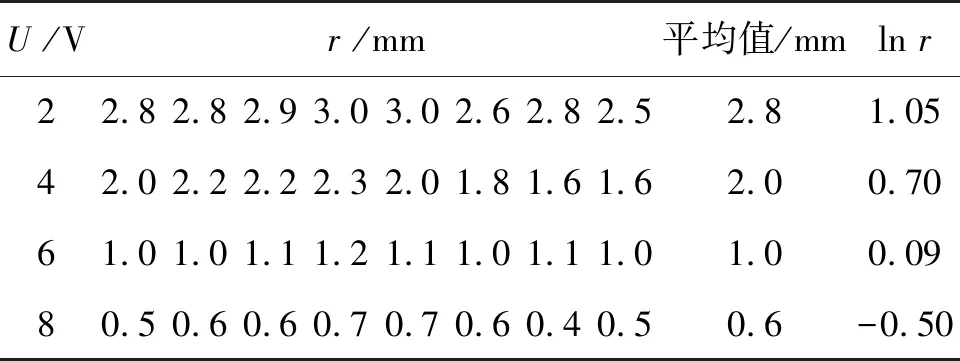
表2 笔式鼠标实验各等势线的数据

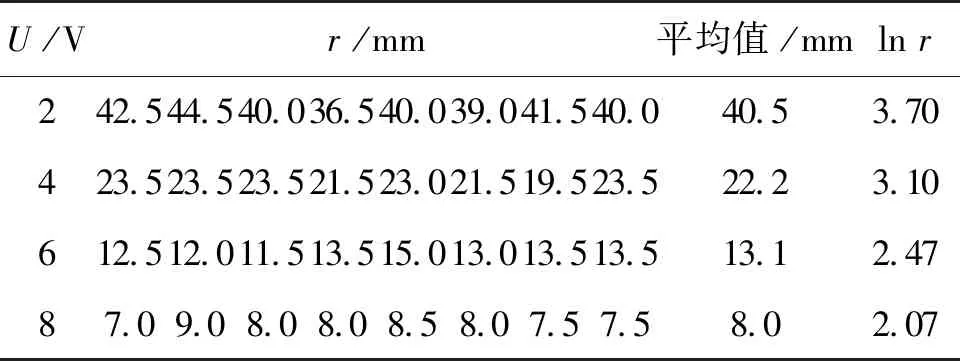
表3 传统实验各等势线的数据

观察表3中传统实验与笔式鼠标实验的数值明显存在较大差异,原因是在笔式鼠标实验中,探测等势点时采用了GGB软件中默认的坐标系,导致金属探针实际移动距离将会等比例的转换到软件坐标系中显示,即软件坐标系与金属探针所在平面坐标系之间的单位长度存在“比例缩放”,因此GGB软件中显示的点的坐标值与金属探针平面坐标值之间会存在“比例系数”,且两坐标系中数值保持一一对应. 因此,在对笔式鼠标所采集实验数据线性拟合时,由式(4)可知,所拟合直线的斜率不会受该比例系数的影响,与在金属探针平面内坐标数据拟合结果相当.

3.2 Origin软件数据处理分析

数据处理可采用各类数学方法[9],本文为进一步研究实验数据的可靠性并简化数据处理过程,将上述数据在Origin中进行线性拟合分析,分别线性拟合传统实验打点数据和笔式鼠标打点数据,并与理论值相比较,如图8所示.本实验运用Origin绘图功能,即将GGB软件记录的数据导入Origin软件中,运用等高线图颜色填充功能,并通过绘图细节调节平滑性,绘制形成二维映射图.同轴电极二维映射图如图9所示.对聚焦电极数据可进行相同数据处理,如图10所示.运用3D颜色映射曲面图功能形成三维映射图,分别作出同轴电极与聚焦电极的三维映射图如图11、12所示.三维图呈现空间立体感,更加形象直观的将电极电场分布呈现出来.

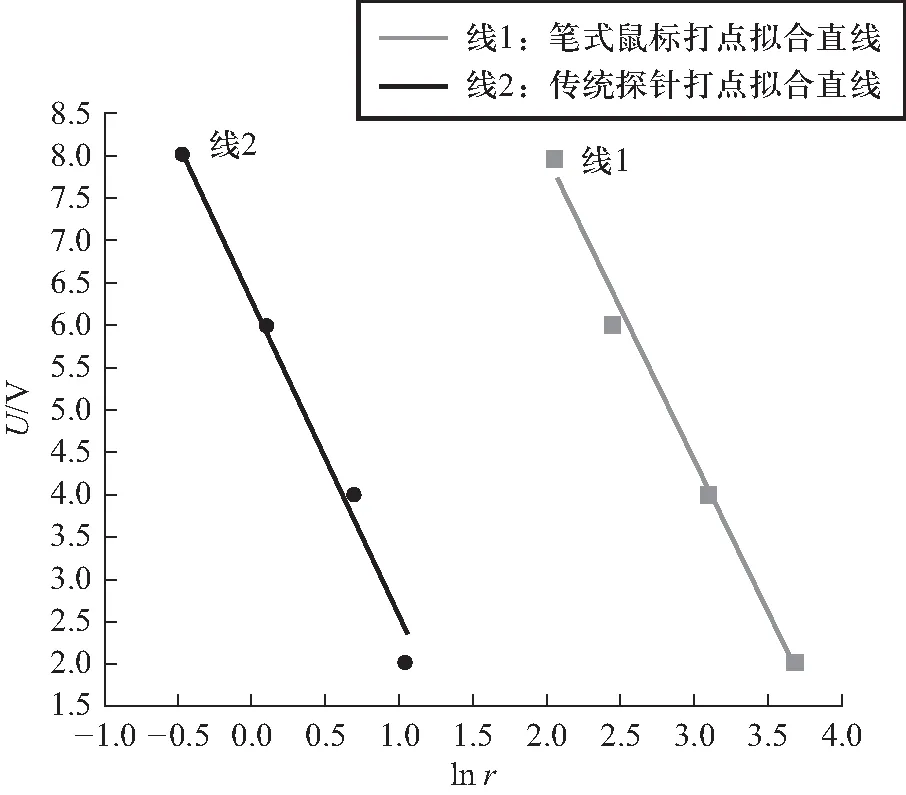
图8 拟合直线

图10 聚焦电极的二维映射图

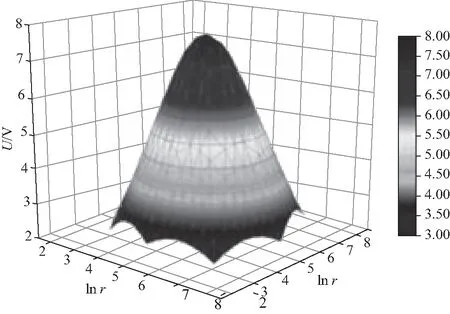
图11 同轴电极的三维映射图

图12 聚焦电极的三维映射图

4 实验误差分析

把两种实验数据拟合方程的斜率k与理论方程斜率比较得知,笔式鼠标实验数据的拟合方程斜率相比传统实验更接近于理论值斜率,相对误差提高了4.1%,笔式鼠标实验数据与理论数据更为接近,这主要是因为采用单层电极架和鼠标探针装置取代传统的双臂探针,消除了因探针不同步而导致的实验误差,消除了双臂探针打点的不确定因素.因此,实验装置的改进,总体减小了实验误差,且使实验数据的稳定性大大提高.但创新的实验的U-lnr方程斜率k仍与理论值之间存在一定的误差,这主要是由于在实验过程中会受以下因素的影响:一是实验所用电表本身的系统误差;二是由于笔式鼠标在探测过程中不能保持相对直立状态,会导致探针与光斑中心产生对准误差.

5 总结

本实验着重从实验装置进行了改造,采用自制带探针的笔式鼠标和微晶导电板结合GGB软件实现了静电场的测量,该装置操作简单可靠,消除了探针不同步导致的实验误差,在保证数据准确度的同时,提高了实验效率,可测量不同形状电极的电场.在模拟静电场的测量、教学和研究方面具有重要意义.利用Origin软件进行数据分析,避免了传统实验采用手绘等势线的较大不确定因素,消除了手工绘图造成的实验误差,增加了实验的严谨性.