三维线性谐振子量子性运动图像的可视化探究

石浚希,范晓鑫,鄂依婷,孔令阳,齐 欣,舒 崧

(湖北大学 物理学院,湖北 武汉 430062)

量子力学通过波函数描述微观粒子的状态,但波函数的统计诠释并不直观,且无法进行直接观测,导致理解上存在一定困难.借助计算机对波函数的量子性图像进行可视化模拟,在量子力学教学中具有重要意义,有助于学生认识微观粒子量子性的运动图像,启发学生深入思考,从而加深对波函数物理意义的理解.

本文将利用蒙特卡罗方法模拟微观粒子的空间概率分布,并通过Mathematica编程软件绘制图像.蒙特卡罗方法是通过不断产生随机数序列来模拟过程的随机模拟方法,也被称为随机抽样技术,主要通过进行统计抽样试验为各种各样的数学和物理问题提供近似解[1].在我们以往的研究中,已经实现了基于蒙特卡罗方法的三维氢原子电子云的可视化[2],在此基础上,本文进一步研究三维量子谐振子图像的可视化.量子谐振子是量子运动体系的基础模型,任何振幅足够小的振动,都可近似看做谐振子的简谐振动,因此其被广泛应用于分子振动、晶格振动、原子核振动、声波传播等体系[3-5].

量子力学课程教学中通常存在概念抽象的问题,即使求解出体系波函数的解析形式,学生仍然难以形成清晰的物理图像.比如,传统《量子力学》教材在讲解量子谐振子时一般侧重波函数的求解过程,忽视了对量子谐振子空间三维概率分布图像的描述.目前,量子谐振子的可视化研究主要通过概率分布函数图像反映或采用等值线图、切片图等形式呈现,存在图像不够直观的问题[6-8].本文利用蒙特卡罗方法对量子谐振子进行可视化模拟,分别绘制直角坐标系和球坐标系下量子谐振子的三维空间可视化图像,借助直观概率云图像对谐振子在不同坐标系下按不同量子数分解方式得到的相应本征模式概率分布的变化情形进行直观对比,研究同一个谐振子体系在不同坐标系下由于量子数分解方式的不同造成的概率云图像的不同表现,分析对应图像的变化规律和造成这种变化的原因.同时,进一步挖掘该体系特有的性质,探索量子力学图像相对经典图像所不同的特性.这有助于深刻理解不同坐标系下由于对称性和守恒量子数的不同考虑对量子谐振子概率分布图像呈现所带来的影响,同时能有效辅助量子力学教学,并开发相应量子力学课程教学资源.

1 三维各向同性谐振子的波函数

为了结合蒙特卡罗方法中的舍选法进行抽样,同时对该系统的性质进行分析,首先需要得到体系的波函数表达式.本文接下来将从三维各向同性谐振子的定态薛定谔方程出发,分别在球坐标系和直角坐标系下对薛定谔方程.

(1)

进行推导得到所需的波函数,以及各自体系中的概率密度函数.

1.1 球坐标系下的表示

球坐标下三维各向同性谐振子势可表示为

(2)

此时薛定谔方程表示为

(3)

考虑拉普拉斯算符的球坐标形式,且薛定谔方程中径向和角向波函数并不存在耦合,因此可以将波函数按径向和角向进行分离变量:

Ψ(r,θ,φ)=R(r)Y(θ,φ)

(4)

对分离变量后所得到的径向和角向微分方程分别求解后得到的关于Y(θ,φ)的函数便是为人熟知的球谐函数

(5)

(6)

(7)

其中N=0,1,2,…,并且有关系式N=2nr+l;m=±1,±2,…,±l.不同于氢原子情况时主量子数n和角量子数l的关系,此时可以出现l大于nr的情况.但同样当N给定时,若nr亦给定,则l也被唯一确定.

综上,此时该体系的波函数可以表示为

Ψnrlm(r,θ,φ)=Rnrl(r)Ylm(θ,φ)

(8)

由波函数的概率诠释可知,该体系在径向上的概率密度函数表示为

WR(r)=|Rnrl(r)|2r2

(9)

角向波函数可以再次对θ和φ进行分离变量,其中和φ相关的方位角波函数Φ(φ)的模方为常数1/(2π),这表明此时的概率云具有绕z轴的旋转对称性.而仰角波函数Θ(θ)对应的仰角方向上的概率密度函数为

Wθ(θ)=|Θ(θ)|2sinθ

(10)

1.2 直角坐标系下的表示

不同于球坐标系,直角坐标系下三维各向同性谐振子势表示为

(11)

类似于球坐标系中的讨论,将此势能项结合式(1)得到直角坐标系下的薛定谔方程表示式.考虑到x、y、z三个方向上波函数不存在耦合,因此可以分离变量为

Φ(x,y,z)=φx(x)φy(y)φz(z)

(12)

分离变量后将得到3个形式完全相同厄米方程,求解得到x轴方向上的归一化波函数为(y轴及z轴方向时的波函数对应于下式中x取y或z)

(13)

综上,此时的体系的波函数表示为

Φnxnynz(x,y,z)=φnx(x)φny(y)φnz(z)

(14)

由波函数的概率诠释可知,该体系在x轴方向上的概率密度函数表示为WX(x)=|φnx(x)|2

(15)

y轴或z轴方向上的概率密度函数有相同数学形式.

上述在2种坐标系下得到的波函数虽分别依赖于合流超几何多项式及厄米多项式,但处于基态时具有相同的波函数形式.但对于非基态的能级,由于两种坐标系下采用2套量子数,因此同一能量下的简并态将因为量子数不同而出现波函数的差异,进而概率云图像将出现差异.

本文接下来将根据2种坐标系下波函数的特性,依靠Mathematica软件编程,利用蒙特卡罗方法进行抽样,绘制出完整的三维可视化图像,对2种坐标系下概率图像进行对比分析并讨论其物理内涵.

2 蒙特卡罗法舍选抽样

蒙特卡罗方法的基本思想是选用恰当的概率模型对待求解问题进行模拟试验,用某种随机变量的分布或统计量作为所求问题的近似解.在采用蒙特卡罗方法进行模拟时,随机抽样过程是决定模拟试验好坏与效率的关键,常用的随机抽样方法有:变换抽样法、舍选抽样法、重要抽样法等.考虑到本文中有多种待抽样的概率密度函数,简便起见,决定采用舍选抽样法进行随机抽样.

舍选抽样法的基本步骤如图1所示,其中g:[a,b]→[0,M]是待抽样的概率密度函数,r1、r2～U(0,1)是2个无关随机数,η为符合概率密度函数g的一个抽样值.

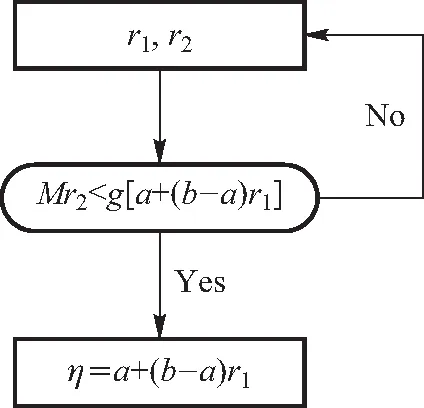
图1 舍选法基本抽样步骤[9]

本文基于Mathematica软件编程,由其内置的伪随机实数生成函数RandomReal产生均匀分布的伪随机数,按图1所示步骤重复进行舍选,最终得到符合概率密度函数g的随机数样本{ηn}.对形如G(x,y,z)=gX(x)gY(y)gZ(z)的高维概率密度函数做抽样,可以按各维度服从概率密度gi(i=X,Y,Z)分别抽样,从而得到服从G分布的一个抽样样本{(ηx,ηy,ηz)n}.

2.1 球坐标系下的舍选抽样

由前文可知,谐振子概率密度函数在球坐标系中可分离为3个正交坐标(r,θ,φ)独立的概率密度函数,即

W(r,θ,φ)=WR(r)WΘ(θ)WΦ(φ)

(16)

其中径向概率密度函数WR(r)由式(9)确定,顶角概率密度函数Wθ:[0,π]→[0,Mθ]由式(10)确定,方位角φ服从其定义域[0,2π]上的均匀分布,即

(17)

显然方位角φ的样本可以直接抽样得到.

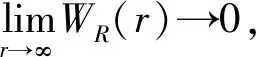
2.2 直角坐标系下的舍选抽样

谐振子概率密度函数在直角坐标系中可分离为3个正交坐标(x,y,z)独立的概率密度函数乘积,即

W(x,y,z)=WX(x)WY(y)WZ(z)

(18)

其中WX、WY、WZ具有相同的形式,定义域均为(-∞,+∞)且均为偶函数.要应用舍选法抽样,必须使定义域截断为有限区间,类似于球坐标系下对径向函数截断的步骤,取正实数xM、yM、zM,使得定义域截断为[-xM,xM].

选取合适的PMi(i=x,y,z)计算得到各维度的定义域边界xM、yM、zM,一般3个边界不一定相等,如要让各维度的抽样范围一致,可以取三者中的最大值aM作为共同的截取边界.按图1的步骤,对WI(I=X,Y,Z)做大量的舍选抽样得到服从WI的随机数样本{xn}、{yn}、{zn},组合得到服从W(x,y,z)的一个随机样本{(x,y,z)n}.

3 两种坐标系下的谐振子概率云图像的对比研究

下面根据谐振子在两种坐标系下不同的量子数分解方式对谐振子的概率云图像进行对比研究.谐振子体系能级为EN=(N+3/2)ћω,对应能量量子数为N,在球坐标系下的量子数分解为nr、l、m,且有N=2nr+l,m=0,±1,±2,…,±l;而直角坐标系下量子数分解为nx、ny、nz,且有N=nx+ny+nz.给定N值时,两种坐标系下的简并度相同,均为(N+1)(N+2)/2,可以得到不同坐标系下的量子数分解模式,具体情形可参见表1.

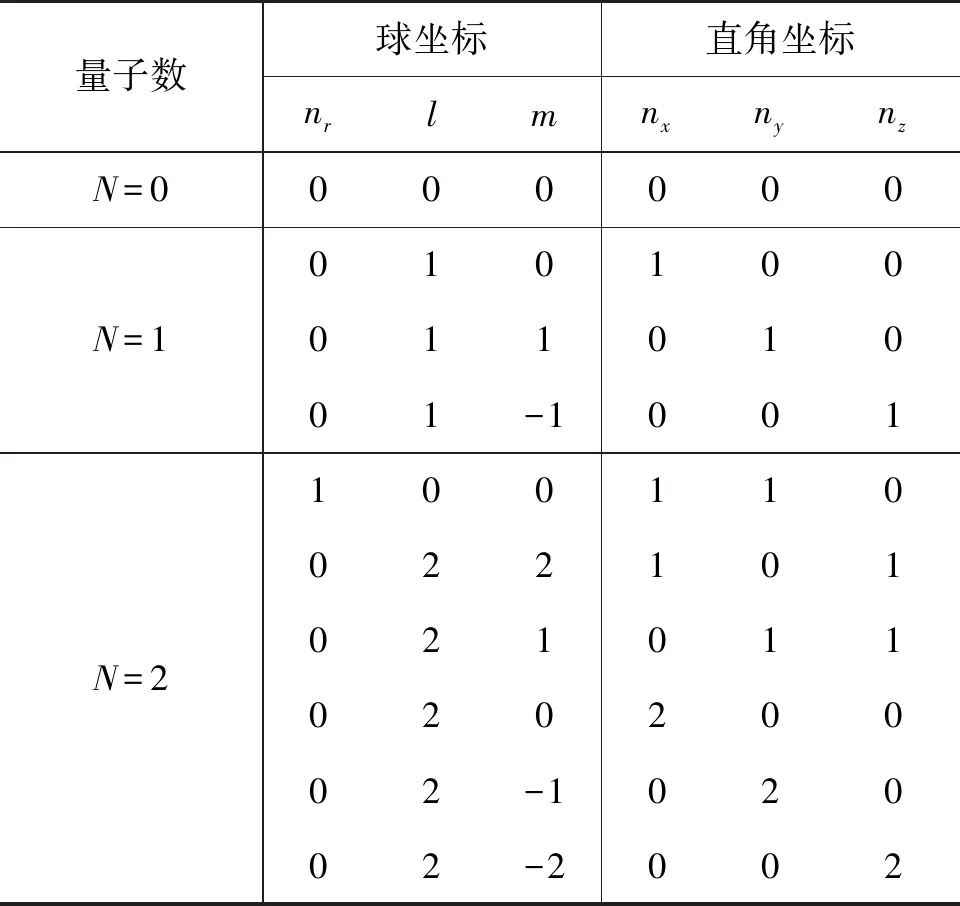
表1 给定N下不同量子数的分解模式

3.1 谐振子基态的对比研究

当N=0时,谐振子处于基态,分别计算直角和球坐标系下的波函数能够得到相同结果,体现在概率密度上有

(19)

这也是基态能量简并度为1的必然结果,但是在两种坐标系下抽样方式是不相同的.对于球坐标系下的抽样,由于角量子数l=0,角向分布各向同性,对于θ和φ的抽样都可以采用均匀抽样,主要是对径向概率密度函数进行舍选抽样.对于直角坐标系,由于3个坐标轴方向概率密度分布都是一样的,所以对3个坐标轴方向上的抽样按照相同的概率密度函数进行舍选抽样.可分别写出球坐标下径向概率密度函数和直角坐标下x轴方向概率密度函数为

(20)

(21)

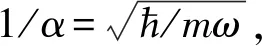
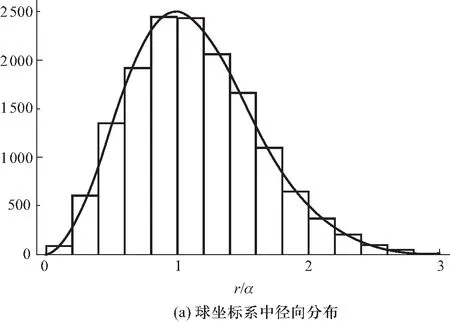
图2 基态抽样概率分布图

从图2中可以看出,在球坐标下径向概率密度函数极大值出现在r=1.0处,而直角坐标下空间概率密度极大值出现在x、y、z等于零处.表面上看似乎两种概率分布给出的谐振子基态运动的空间图像是不同的,但仔细分析球坐标下径向概率密度函数的含义发现,径向概率密度中实际上包含了不同方向的概率贡献,应该理解为某径向距离r处单位径向距离的球壳层中的概率,将这个概率除以球壳表面积4πr2才得到该径向距离球面上特定空间点处的概率密度,而这与直角坐标下的概率密度函数是相同的.所以两者虽然抽样方式不一样,但是最后给出的抽样结果在空间中给出的概率分布图像是一致的,我们的实际抽样结果也证实了这一点.

取一次抽样所得样本绘制如图3所示,所绘的概率云图像以正视图、顶视图和缺省视图横向排列为一组,图中点越密集的地方代表了粒子在该处出现可能性越大.从图中可以看出概率云中心位置密度最大,从中心向外围密度逐渐减小,呈现出球对称分布.所以基态谐振子最可能出现的位置是r=0处,即谐振子经典条件下的平衡位置.

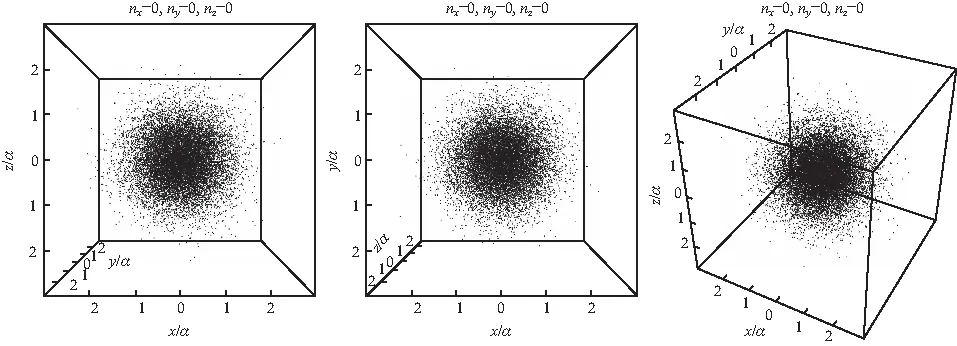
图3 和的概率云图

3.2 谐振子激发态的对比研究

当N=1时,谐振子处于第一激发态,能级简并度为3.按照表1中球坐标系和直角坐标系下量子数进行分解,各得到3个量子态.对于球坐标系下的3个态,考虑其中磁量子数m=±1的两个态,从波函数角度看这两个态的角动量方向不同,但是由于两者的概率密度函数满足

(22)

图4 概率云图

(23)

即球坐标系下量子数nrlm取010的态与直角坐标系下量子数nxnynz取001的态是同一个态,这在激发态情形下是一种特殊情况.

当N=2时,谐振子处于第二激发态,能级简并度为6.按照表1中球坐标系和直角坐标系下量子数进行分解,各得到6个量子态.同样考虑到其中部分量子态的概率云存在相似性,我们只选取球坐标系下Ψ100、Ψ020、Ψ021、Ψ022和直角坐标系下Φ110、Φ002对应的量子态来进行抽样,并绘制出对应概率云图像的缺省视图如图5所示.

和概率云图

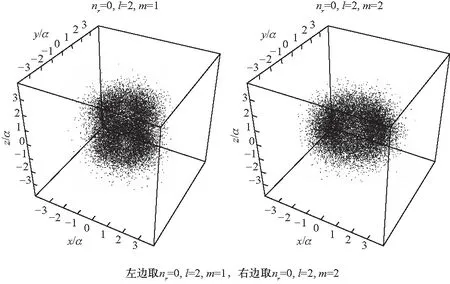
和概率云图

和概率云图

4 总结与展望

本文通过求解量子力学中三维各向同性谐振子的球坐标及直角坐标下的波函数,结合蒙特卡罗方法中的舍选法绘制出了两种坐标系下不同量子数分解下的概率云图像,并根据不同坐标系下波函数的特点对不同概率云图像的特征进行了对比分析,从中我们可以得到如下结论:对于三维谐振子体系,在能量守恒和角动量守恒条件下,量子谐振子具有非常丰富多样的运动模式.不同坐标系的选择意味着不同物理守恒量的选取,会造成量子态本征模式分解的不同.由于守恒量通常对应实际物理测量量,所以本文所讨论的不同本征模式实际上对应实验中在按不同守恒量集合方式进行测量后可以得到的不同量子本征态.从中我们可以理解到对于同一个量子谐振子系统,按不同的测量方式进行测量会影响到系统,使它最后呈现不同量子态模式的空间运动状态.同时,由量子场理论我们知道简并度的消除意味着系统对称性的自发破缺,这里如果由于测量造成系统处于不同的本征态实际上是系统的对称性发生了自发破缺,而球坐标系下和直角坐标系下本征模式的不同,也表示实际测量中如果按不同的测量量方式进行测量,系统在测量过程中对称性的破缺方式以及测量后得到的破缺状态结果也是不同的.关于对称破缺的深入研究在量子场论体系中具有重要意义.

另外从量子力学教学资源开发角度来说,我们以后还会进一步研究含有微扰和自旋效应的量子力学体系的可视化,并在未来对量子力学课程的可视化教学资源进行系统的开发,设计并发展出量子力学体系可视化相应软件,促进量子力学课程的教学,帮助学生更好学习和理解量子力学.