一般多普勒效应的综合统一分析

周 强,刘 静,李 鹏

(山东科技大学 电子信息工程学院,山东 青岛 266590)

在物理学教材中分别给出了声波和光波的多普勒效应公式,但两者表达式不同.一些文献分析了两者间的联系[1,2],之所以称为联系,是因为没有真正地将两者统一起来,而是将光速c“换成”声速u或将声速u“换成”光速c,这样处理称为统一有些牵强,称作联系更为恰当;另一些文献虽然作了统一分析[3-5],但均是在特殊洛伦兹变换下讨论问题,所得结果又不具有一般性.本文在不区分声波与光波的情况下,基于波动传播的共同本质,综合运用多种方法导出一般多普勒效应的3个等价表达式,系统地论证两者的统一性,并由此分析声波和光波的多普勒效应.

由于声波只能在介质中传播,光波可以在真空中传播,为了能够作统一分析,与传播声波的介质对应,分析光波的传播需设置一个中介,所以统一地分析多普勒效应要涉及3个参考系:介质系(或某一中介系)KM、波源系KS、接收器系KD.而由于3个参考系间的相对速度很难保证都与某一坐标轴(如x轴)平行,为此需分析参考系间的相对速度不沿某一坐标轴方向上的一般情况.

1 基于四维波矢的一般洛伦兹变换的分析

1.1 三个一般多普勒效应公式的导出

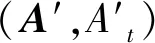
(1)

(2)

据以上2式得,由K系中四维波矢(k,iω/c)到K′系中四维波矢(k′,iω′/c)的一般变换式为

(3)

(4)

其中k=kk0=ωk0/u,u为K系中的波速.

如图1所示,在KM系中,KS、KD系的运动速度分别为vS、vD,波矢为kM,vS、vD与kM方向间的夹角分别为θS、θD.

取K=KM、K′=KS,由式(4)得,波源S的本征发射角频率ωS与KM系中波的角频率ωM之间的关系式为[3,4]

(5)

取K=KM、K′=KD,由式(4)得,接收器D的本征接收角频率ωD与KM系中波的角频率ωM之间的关系式为[3,4]

(6)

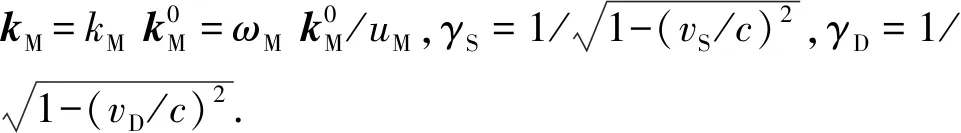
(7)

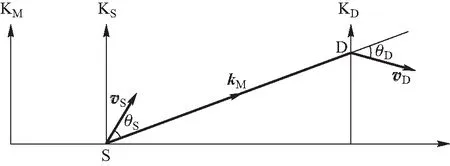
图1 在KM系中KS系、KD系的运动及波的传播

如图2所示,在KS系中,KD系的运动速度为vDS,波矢为kS,vDS与kS方向间的夹角为θDS.

取K=KS、K′=KD,由式(4)得[4]

(8)

其中

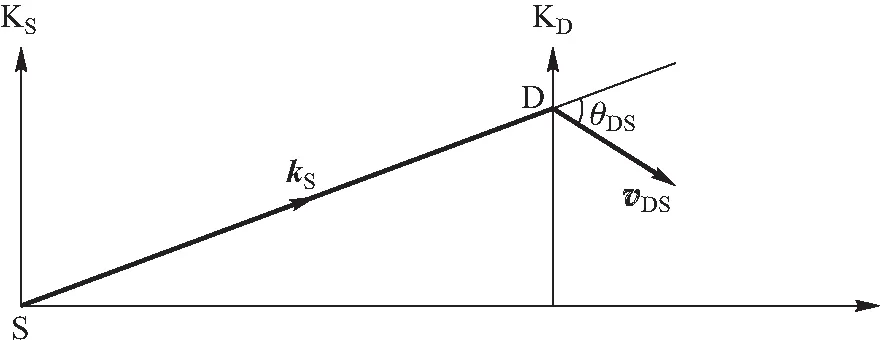
图2 在KS系中KD系的运动及波的传播

如图3所示,在KD系中,KS系的运动速度为vSD,波矢为kD,vSD与kD方向间的夹角为θSD.

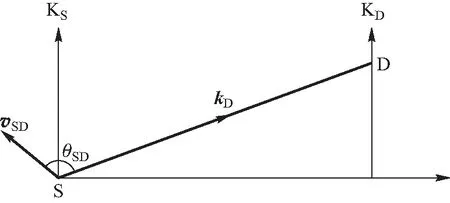
图3 在KD系中KS系的运动及波的传播

取K=KD、K′=KS,由式(4)得[4]

(9)

其中

式(7)—式(9)即为一般多普勒效应的3个表达式.

1.2 三个一般多普勒效应公式的关系

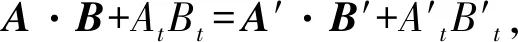
由上述性质得,在KS系和KM系中,接收器D的四维速度与四维波矢的标积相等,即有

(γDSvDS,iγDSc)·(kS,iωS/c)=

(γDvD,iγDc)·(kM,iωM/c)

由此得

上式与式(5)相除得

(10)

将上式分别与式(7)、(8)对比可见,式(7)与(8)等价.

同理,在KD系和KM系中,波源S的四维速度与四维波矢的标积相等,即有

(γSDvSD,iγSDc)·(kD,iωD/c)=

(γSvS,iγSc)·(kM,iωM/c)

由此得

上式与式(6)相除得

(11)

将上式分别与式(7)、(9)对比可见,式(7)与(9)等价.

由式(10)、(11)再得

(12)

将上式分别与式(8)、(9)对比可见,式(8)与(9)等价.

可见式(7)—式(9)是相互等价的3个表达式.

1.3 三个一般多普勒效应公式中物理量间的关系

首先分析vDS、vSD与vS、vD间的关系.

设质点相对于K、K′系分别以速度V、V′运动,则其四维速度分别为(γVV,iγVc)、(γV′V′,iγV′c).由式(1)、(2)得,质点速度、速度因子由K系到K′系的一般变换式为

(13)

(14)

另由式(14)解得

(15)

可见,若V=c则V′=c,即质点速率满足光速不变原理.

将式(13)用于图1中得,vDS、vSD与vS、vD的关系式为

(16)

(17)

若取K=KS、K′=KD(见图2),则v=vDS;设质点静止于K=KS系中,则V=0、V′=vSD.由式(13)可得vSD=-vDS(或由相对性原理直接得到).

(18)

由式(15)可得,vDS、vSD的大小为

其次分析波矢kS、kD、kM间的关系.

将式(3)用于图1中得,波矢kS、kD、kM间的关系式为

(19)

(20)

将式(3)分别用于图2、图3中得,波矢kS与kD的关系式为

(21)

(22)

另外,分别将波矢k、k′分解为平行于和垂直于K′系相对K系运动速度v方向的分量和,由式(3)得

(23)

k′sinθ′=ksinθ

(24)

其中θ、θ′分别为k、k′与v方向间的夹角.

分别对以上两式的两端求平方和得

(25)

此即为波数由K系到K′系的一般变换式[5].

将上式用于图1中得,波数kS、kD与kM的关系式为

(26)

(27)

将式(25)分别用于图2、图3中得,波数kS与kD的关系式为

(28)

(29)

再来分析波速uS、uD、uM间的关系.

式(4)与(25)相除,由u′=ω′/k′得

(30)

此即为波速由K系到K′系的一般变换式[5].可证,若u=c则u′=c,即波速亦满足光速不变原理.

将上式用于图1中得,波速uS、uD、uM的关系式为

(31)

(32)

将式(30)分别用于图2、图3中得,波速uS与uD的关系式为

(33)

(34)

最后分析波行差关系.

式(23)与式(24)相除得

(35)

此即为一般的波行差表达式之一[3].

另外式(4)的逆变换式为

其中k′=k′k′0=ω′k′0/u′,u′为K′系中的波速.

上式与式(4)相乘得

(36)

此即为一般的波行差表达式之二[4].

可以证明(略),式(35)与(36)等价.由其可得KM、KS、KD系间的波行差关系,如由式(36)可得KS系与KD系间的波行差关系式(12).

由本小节中的各关系式可验证前两小节中相关结果的正确性,如式(31)、(26)相乘可得式(5),式(32)、(27)相乘可得式(6),式(33)、(28)相乘可得式(8),式(34)、(29)相乘可得式(9);而由式(16)、(18)、(19)、(26)、(31)可验证式(10),由式(17)、(18)、(20)、(27)、(32)可验证式(11),由式(21)、(28)、(33)或(22)、(29)、(34)可验证式(12)(略).

2 基于波的三个特征物理量关系的分析

2.1 有效波速概念的引入

有了上述认识,便可引入有效波速的概念.根据波动理论,角频率ω、波速u、波数k间的关系式为ω=uk,由该式分析多普勒效应,采用有效波速的概念比较方便.所谓“有效”意指:接收器“能接收到”来自波源的波,因对波源发出的球面波,只有沿波源与接收器连线方向上的那一部分波才能被接收到,所以沿两者连线方向上波相对波源或接收器的传播速率称为有效波速[7,8],分解说明如下.

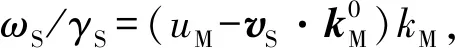
2.2 由有效波速分析多普勒效应

如图1所示,在KM系中分析波分别相对于KS、KD系的传播,其中该系中的波数kM=ωM/uM.

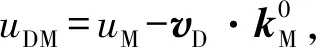
由时间膨胀公式得ωSM=ωS/γS、ωDM=ωD/γD,分别代入以上两式即得式(5)、(6).

同上节,由式(5)、(6)自然得到式(7).

如图2所示,在KS系中分析波相对于KD系的传播,其中该系中的波数kS=ωS/uS.

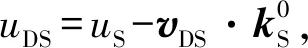
而由时间膨胀公式得ωDS=ωD/γDS,代入上式即得式(8).

如图3所示,在KD系中分析波相对于KS系的传播,其中该系中的波数kD=ωD/uD.

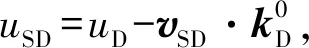
而由时间膨胀公式得ωSD=ωS/γSD,代入上式即得式(9).

由本小节论述可知,式(7)、(8)、(9)分别是在KM、KS、KD系中分析所得的3个表达式.

3 基于相位不变原理的一般洛伦兹变换分析

由一般的四维矢量标积不变性还可得,四维波矢(k,iω/c)与四维坐标(r,ict)的标积在一般洛伦兹变换下保持不变,即k·r-ωt=k′·r′-ω′t′,此即为一般的相位不变原理.

由(1)、(2)的逆变换得,由K′系中四维坐标(r′,ict′)到K系中四维坐标(r,ict)的一般变换式为

据以上两式可得,由K′=KS中四维坐标(rS,ictS)到K=KM中四维坐标(rM,ictM)的变换式(见图1),将其代入相位不变式kS·rS-ωStS=kM·rM-ωMtM中,由等式两端tS项的系数相等即得式(5)(略).

同理可得,由K′=KD中四维坐标(rD,ictD)到K=KM中四维坐标(rM,ictM)的变换式(见图1),将其代入相位不变式kD·rD-ωDtD=kM·rM-ωMtM中,由等式两端tD项的系数相等即得式(6)(略).

同前,由式(5)、(6)自然得到式(7).

而将由K′=KD中四维坐标(rD,ictD)到K=KS中四维坐标(rS,ictS)的变换式(见图2)代入相位不变式kD·rD-ωDtD=kS·rS-ωStS中,由等式两端tD项的系数相等即得式(8)(略).

同理,将由K′=KS中四维坐标(rS,ictS)到K=KD中四维坐标(rD,ictD)的变换式(见图3)代入相位不变式kS·rS-ωStS=kD·rD-ωDtD中,由等式两端tS项的系数相等即得式(9)(略).

4 基于波脉冲发射、传播及接收瞬时过程的分析

设波源在本征时间dtS内发出一波脉冲,接收器在本征时间dtD内接收到这一波脉冲,则两者的相位增量相等[7],即有

ωSdtS=ωDdtD

(37)

如图4所示,在KM系中分析波脉冲的发射、传播及接收的瞬时过程,其中接收器在时间dt2内接收到波源在时间dt1内发射的波脉冲,则由式(37)可得式(7)(略).

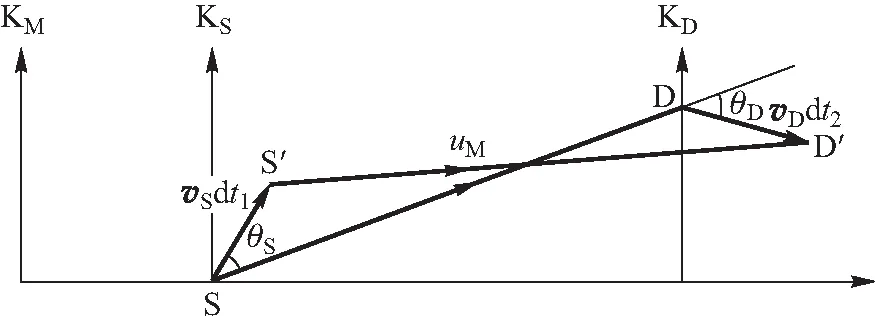
图4 在KM系中波脉冲的发射、传播及接收的瞬时过程

图5 在KS系中波脉冲的发射、传播及接收的瞬时过程

如图6所示,在KD系中分析波脉冲的发射、传播及接收的瞬时过程,其中接收器在本征时间dtD内接收到波源在时间dt′S内发射的波脉冲,则由式(37)可得式(9)(略).

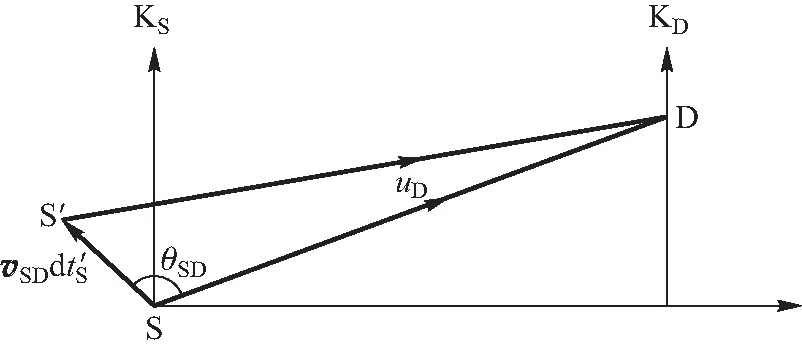
图6 在KD系中波脉冲的发射、传播及接收的瞬时过程

5 结果分析

综上所述得,共同结果式(7)—式(9)分别为在KM、KS、KD系中分析所得的3个相互等价的一般多普勒效应公式.即如同物体相对于不同参考系的运动不同一样,多普勒效应相对于不同参考系也有不同的表达式,这些表达式虽然形式不同但相互等价.现分析其在光波和声波中的具体应用.

对真空中的光波,分别将uM=c代入式(31)、(32)得uS=uD=c,则由式(7)—式(9)得

(38)

(39)

(40)

其中式(40)是教材中的常见公式[7,9].

另外,文献[1]认为式(39)、(40)是式(38)的特例.由式(7)—式(9)相互等价得,式(38)—式(40)也相互等价(也可将uM=uS=uD=c分别代入式(19)—式(22)、式(26)—式(29),用类似1.3小节中所述方法验证(略)),不是一般与特例的关系.

对介质中的光波,式(7)中的uM=c/n,其中n为介质的折射率,式(8)、(9)中的uS、uD由式(31)、(32)确定.

对于声波,则需作相关表达式的低速近似.由vS、vD、vSD、vDS<

(41)

(42)

(43)

其中式(41)在教材中可以找到[7,9].

另外,将上述低速条件分别代入式(16)、(17)得vDS=vD-vS、vSD=vS-vD,此即为经典的质点速度合成公式;分别代入式(31)—式(34)得uS=uM-vS·k0=uD-vSD·k0、uD=uM-vD·k0=uS-vDS·k0,此即为经典的波速变换式.由这些结果可验证式(41)—式(43)相互等价(略).

由于式(38)中涉及某一中介系KM中的速度vS、vD,表观上易造成光波依靠中间介质传播的假象;而式(39)、(40)则由波源与接收器的相对速度vSD、vDS表示,表达形式简洁明了.但式(39)使用起来不如式(40)直截了当,如对光的横向多普勒效应,将θSD=π/2直接代入式(40)即得ωD=ωS/γSD,但要用式(39)计算,需先将θSD=π/2、uS=c代入波行差公式(12)解得cosθDS=vDS/c(也可由式(35)求得),然后再代入式(39)才能得到相同的结果.这应该是教材中只有式(40)的原因.

而由于式(41)中显含介质系KM中的波速uM,与声波的传播需要介质相吻合;反而式(42)、(43)因通过uS、uD隐含了uM,表观上易造成声波可以脱离介质传播的假象.这也应该是在教材中只能找到式(41)的原因.