稳态法测量冰导热系数的实验研究

黄嘉豪,王英连,廖旭辉,雷 霆,万烨然,赖文标

(景德镇陶瓷大学 机械电子工程学院,江西 景德镇 333403)

导热系数是物质导热能力的标志,通常表示在稳定传热条件下,1 m厚的材料,两侧表面的温差为1 K或1 ℃,在单位时间内,通过1 m2面积传递的热量. 对不同物质导热系数的测定,有助于更好地科学利用它们.20世纪90年代,李志军等人自制实验装置,采用加热灯泡配合风扇搅拌的方法获得所需环境温度,测量了海水冰的导热系数[1].2009年,蔡亮等通过计算机方法模拟了霜层冰晶的生长过程,并计算得到了导热系数[2]. 2018年,孙始财等利用Hot Disk热常数分析仪研究了冰生消过程中导热系数的变化规律[3]. 近年来,关于冰的导热系数的研究相对较少,测量方法主要采用传统的稳态铜盘加热法[4,5]. 本实验基于傅里叶提出的热传导方程,推得适用的导热系数公式,采用热功率可控的加热垫取代铜盘,进行了实验方案设计及实际测量,降低了成本,简化了数据处理,方便可行.

1 实验原理

(1)

式(1)也称为傅里叶热传导定律. 其中,dQ为热量改变量,dt为时间变化量,dT为温度改变量,dδ为传热距离变化量,S表示导热面积,λ称为导热系数,单位为W/(m·K). 稳态传热时有

(2)

图1 稳态平板法原理示意图

稳态平板法指出当物体内部存在温度梯度时,热传导过程就会发生,热量从高温区向低温区传递. 本实验改进装置,采用热功率可控的加热垫取代平板法中的铜盘,给待测冰加热使其温度升高,热量通过待测冰由高温一侧向低温一侧传递. 绝热环境下,当发热层温度恒定时,单位时间内发热层的发热量和通过待测物体的导热量相等. 故适用于本实验的导热系数公式由式(2)可得

(3)

(4)

其中,I为发热电流,R为发热电阻,d为待测冰厚度,S为待测冰面积,ΔT为稳态传热时待测冰两面温差.

2 实验方案

实验装置示意图如图2所示,将待测冰置入带有发热垫的绝热装置中,冰两侧各自接有温度传感器,待两侧温度相等时,接通电源,发热垫紧贴的一侧温度上升,待冰两侧达到稳定温差ΔT时,记录电流示数I和此温度下的阻值R,代入式(4)即可求出冰的导热系数.

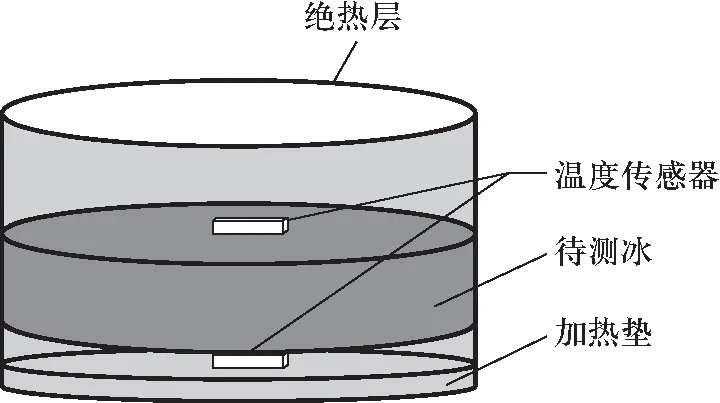
图2 实验装置示意图

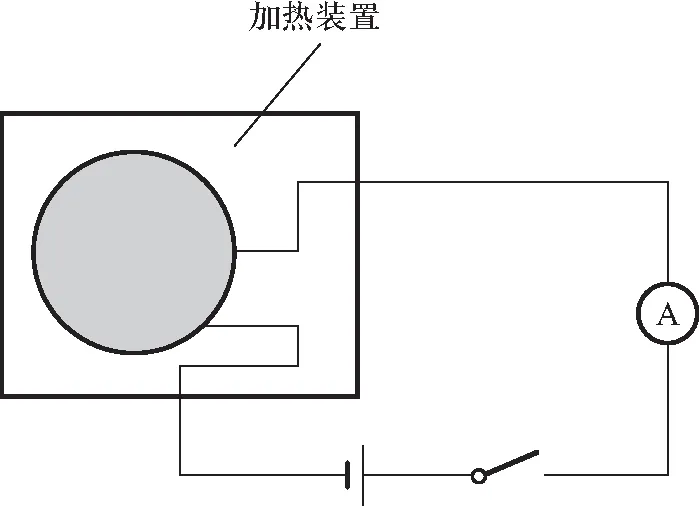
图3 加热装置示意图

传统的稳态平板法是采用安装加热铜盘和散热铜盘来获得温差的[5,7],而本实验的加热装置是一块两端通电的圆盘形状的均匀发热垫,通过改变电压控制其加热功率. 加热装置如图3所示,在确保热量轴向均匀传递的同时简化了实验装置,操作便捷,降低成本. 同时在待测冰的外围进行了绝热处理,以减小横向传热对实验结果的误差影响.本实验分别通过改变待测冰的直径与厚度比值、环境温度和含盐率3个方面进行冰的导热系数测定及影响因素研究.

3 实验结果及分析

3.1 直径厚度比的影响

待测冰呈圆盘形状,直径用D表示,且D= 12.0 cm,厚度用d表示,分别取2.0 cm、1.5 cm、1 cm、0.8 cm和0.5 cm,直径厚度比值与导热系数的关系及相对误差E如表1所示.

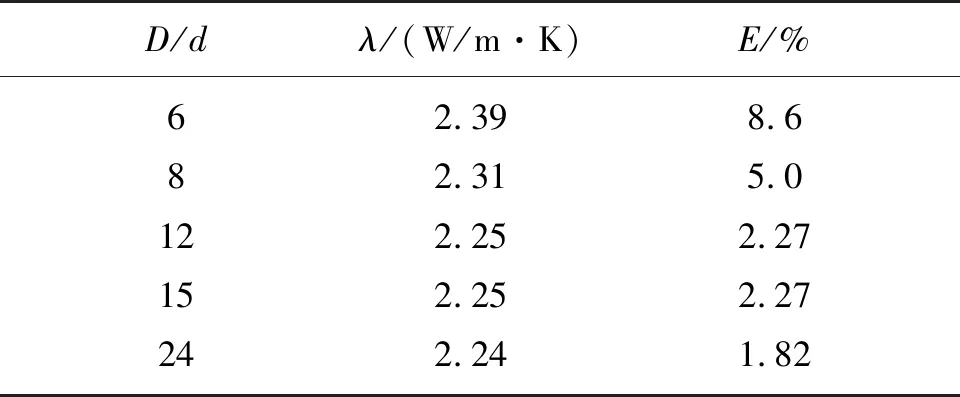
表1 直径厚度比值与导热系数关系

测量结果表明,随着直径厚度比值D/d的增大,导热系数逐渐减小并接近真实值2.20 W/(m·K),但D/d越大,待测冰厚度越小,厚度不均造成测量结果偶然性误差所占比例就增大,同时厚度越薄,制冰、取冰等具体操作环节更加不便,反而容易造成更大的测量误差. 兼顾操作性和准确性综合来看,本实验在待测冰的直径厚度比值D/d为12时,测得导热系数的最佳值为2.25 W/(m·K).

当这一比值D/d小于12时,导热系数偏差较大,这是因为此时冰的厚度大,通过冰的侧面积进行的热量传递不可忽略,导致总热量既包含纵向传热也伴随横向传热,且横向传热功率占总传热功率的比例较大,进而使得所测导热系数偏大. 这与孟祥睿等人对导热系数的影响因素分析中得出的结论一致[5,7].

当D/d大于12时,冰的直径一定,厚度减小,侧面散热功率相比于总传热功率所占比例迅速减小,导热系数趋近于一个稳定值,如图4所示,但仍存在一定波动偏差,综合各类不确定度分析,测量结果的相对不确定度为2.61%.

图4 直径厚度比值D/d与导热系数关系曲线

3.2 环境温度的影响

本组实验中,圆形冰的直径D= 12.0 cm,厚度d=1cm,环境温度分别选取-4.0 ℃、-8.0 ℃、-10.0 ℃、-12.0 ℃ 和 -16.0 ℃. 环境温度T与导热系数的关系及相对误差E如表2所示.

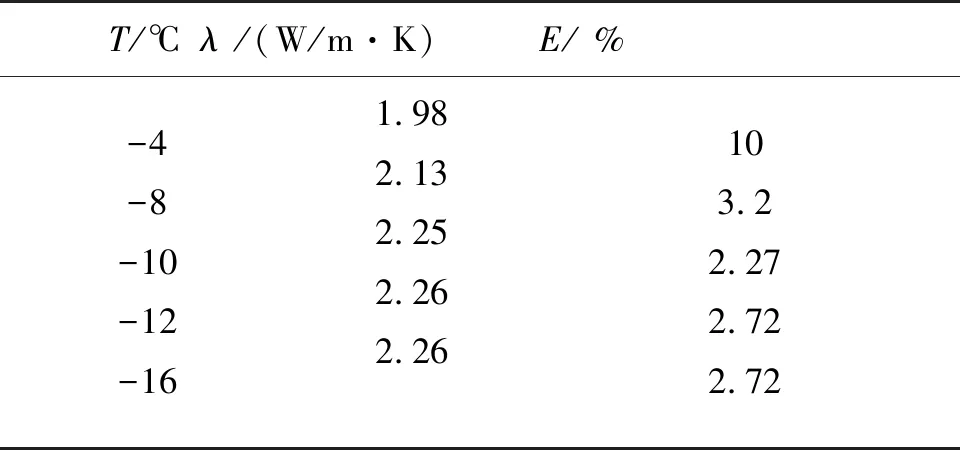
表2 环境温度与导热系数关系

表2中结果表明一定温度范围内,导热系数随环境温度的降低而增大,且增大的速率随环境温度的降低而放缓. 这是因为随着温度的降低,冰的结构更加紧密,当冰两侧有温差时,冰中的晶体结构能够更快地把振动传给下一个分子,使得传热速率更大,导热系数增大[8]. 从另外一方面来讲,随着温度的升高,冰内分子无规则热运动速率增加,不断发生碰撞,造成能量损失,影响了热量的传递效率,从而使导热系数减小. 本实验条件下,环境温度在-10 ℃时冰的导热系数最接近真实值. Huang W等人[9]指出冰晶形成过程中的生消反应会产生气泡,且随着环境温度的降低,生消反应得到有效抑制,气泡含量减少并趋于稳定,从而使得导热系数趋于一个稳定数值. 图5正是呈现这一趋势.

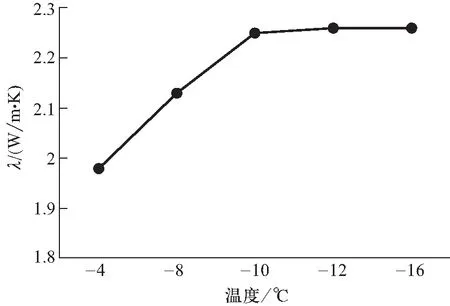
图5 环境温度与导热系数关系曲线

3.3 含盐率的影响

本组实验研究杂质含量(含盐率)与导热系数的关系. 待测冰的直径D= 12.0 cm,厚度d=1 cm,环境温度 -10.0 ℃,含盐率分别选取0、1.25%、2.50%、3.75%和5.00%.含盐率与导热系数的关系及其不确定度U如表3所示.

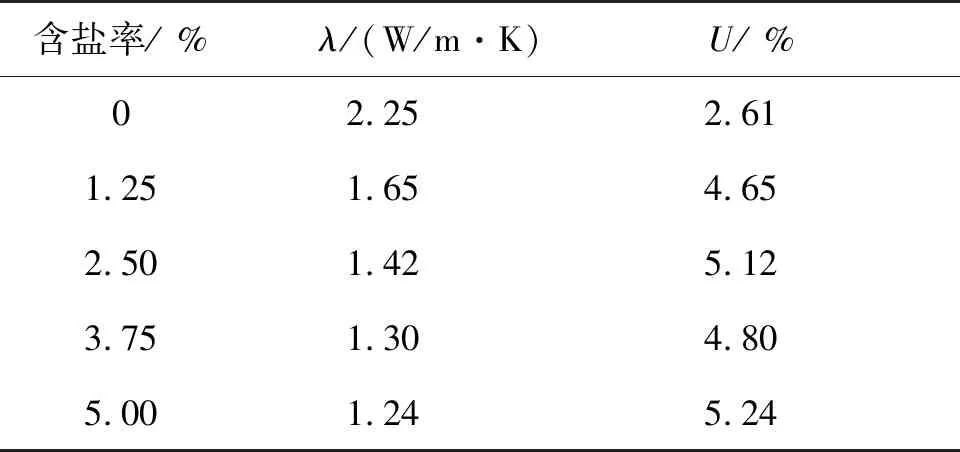
表3 含盐率与导热系数关系

表3结果表明,随着含盐率的升高,盐水冰的导热系数不断减小,这与李怀科[10]等人关于不同浓度盐水导热系数的实验结论相一致. 由表3可知,含盐率5.00%的盐水冰的导热系数相比于纯水冰显著下降,降至1.24 W/(m·K),各浓度盐水冰的测量结果的相对不确定度均在5%左右.

本实验盐水冰在冻结过程中,水体中的溶解氧不能迅速释放,而被冻结镶嵌在冰晶中,所以会有大量空气泡存在,且其含量和分布比较随机,而这些气泡的导热系数远小于纯水冰;另一方面,由于盐水冰的冰点低于0 ℃,在持续的低温环境下,分子将自身排列成水合物的硬性晶格结构,含盐率不同,冰点不同,内部结构复杂程度也会随盐分相应改变,影响到了规则冰晶的排布及传热性能,导热系数这一物理性能指标也会受其影响[11,12],最终呈现图6所示的变化.

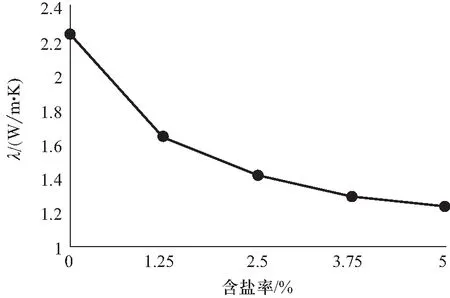
图6 含盐率与导热系数关系曲线

4 小结

本实验基于傅里叶提出的热传导方程,采用热功率可控的加热垫取代铜盘,最终实现了冰的导热系数的测量及相关影响因素的研究. 研究发现,稳态法进行导热系数的测量影响因素较多,如实验参数设定、测量仪表精度、待测冰的尺寸、平整度和结晶度等. 随着待测冰厚度的增加,侧面导热量所占比例迅速增加,可以在减小两侧温差的同时尝试对适用公式进行修正. 另外,测温点的分布和选择也至关重要,可尝试多点测温或面积测温以减小实验误差.

目前,尚未查阅到不同浓度盐水冰的导热系数的公认值,只有通过不断优化测量方法、提高仪器精度、修正适用公式和重复实验等,来继续进行导热系数的测量及原理探究,以期达到理想效果.