基于高端复合人才培养目标探索线性代数教学改革

李冬果，高 磊，郑文新，李 林

首都医科大学生物医学工程学院（北京 100069）

为适应我国社会主义现代化建设和卫生事业发展需要、满足社会对拔尖创新医学人才的需求，首都医科大学自2021 年开始创办临床医学、口腔医学专业学术学位博士水平的专业教育（简称阶平班），旨在培养具有独立从事科学研究与创新能力、创造性和国际视野、未来具有推动和引领医学发展的临床医学高端复合型人才[1]。其特殊定位要求学生在本科阶段获得扎实的数理基础和学习数理知识的能力，同时基本运算、抽象思维、逻辑推理及解决实际问题的能力也能得到系统的培养，使学生了解数学方法与数学建模技术在生物医学中的应用，为后续课程的学习和将来从事的医药临床或科研工作奠定数学基础。

首都医科大学阶平班的培养模式有别于国内外同样定位的专业培养，即高中起点的具备临床专业水平、博士科学学位八年制教育。因此探索符合培养目标需求的人才培养体系对于医学教育改革至关重要。线性代数作为大学数学的主干课程，在课程内容、教学模式与方法等方面的改革面临全新的挑战。本研究基于先前的医用高等数学教育与研究[2-4]，依据阶平班的培养目标和计划，对线性代数课程教学模式进行初步探索，并对教学理念和教学方法开展相关教学实践。

1 线性代数课程在专业培养目标中的功能定位

阶平班临床医学专业的培养目标定位于“具有独立从事科学研究工作的能力，创造性地研究和解决本学科中的有关理论和实际问题；在科学或专门技术上做出创造性的成果”“具有为新知识产生、新技能的发现做出贡献的意识”[1]。基于此确定线性代数的课程教学目标，分为知识目标、能力目标和素质目标。知识目标中明确了基本概念、基本理论等教学内容的深度和广度，要求学生理解和掌握线性空间理论、线性空间上的线性映射及线性变换理论，以及矩阵空间的基本理论等。能力目标要求培养学生基本运算、抽象思维、逻辑推理，以及能够综合运用所学知识分析和解决实际问题的能力。素质目标要求学生了解数学思维与数学方法在生物医学中的应用，并通过在教学中融入适当的思政元素，帮助学生树立正确的价值观，提升民族自豪感的同时，使学生认识到要成为对国家、对社会有用之才必须要学好、用好数学。

2 线性代数课程教学内容

北京大学丘维声教授在其编著的《简明线性代数》中指出：“线性代数是研究线性空间与线性映射的理论，它的初等部分是研究线性方程组和矩阵”[5]。国内外许多线性代数教材就基本内容而言，差异不大，都是以线性方程组为主线，以矩阵和向量为工具，来阐明线性代数的基本概念、基本理论和基本方法[5-7]。依托这些教材，线性代数课程教学直接从行列式或矩阵入手，以线性方程组的消元法为引例，直接给出行列式和矩阵这两个概念及其运算。那么行列式和矩阵的本质究竟是什么？行列式为什么会有如此“怪异”的计算规则？矩阵的乘法规则为什么如此规定？为什么这样一种“怪异”的乘法规则却能够在实践中发挥如此巨大的功效？行列式与其对应的方阵本质上又是什么关系？特征值和特征向量定义中为什么单一数λ 的效应等同于一个诺大的矩阵效应？这些问题对于学生而言是晦涩难懂的抽象概念、复杂的公式和难以理解的定理及其证明，学生只是被动地记忆理解，而无法领略线性代数内涵的美妙、和谐与统一，导致课程教学效果不理想。正如瑞典数学家Lars Garding 在其名著EncounterwithMathematics中提到：“如果不熟悉线性代数的概念，要去学习自然科学，现在看来就和文盲差不多”[8]。因此，学生学习中已存在的问题成为线性代数课程教学内容改革的直接动因。

2.1 以线性空间为主线设置教学内容的必要性与可行性

目前高等学校非数学类专业较少接触现代数学，而数学课程的主要内容基本上都是17—18世纪变量数学时期奠定的[9-10]。在本科阶段引入现代数学是非常好同时又极具挑战的事情。阶平班是一个特殊的群体，肩负着特殊的使命，在其基础教育阶段尽可能地引入现代数学思想。但在教学内容设置和教学过程中要创造性地解决现有问题也将面临诸多困难。在面向医学生开设的线性代数课程传统教学内容中，设置一部分自学内容，同时引入现代数学思想，即以线性空间为主要内容的系列知识群构建教学内容有必要而且可行。

依据首都医科大学阶平班培养目标，在选择教学内容和实施教学时应注意教学内容对学生而言应该是全新的。线性代数中的矩阵、线性方程组其实都不满足这一点。对学生而言，具有对新概念逐步发展的思路建立在集合论基础上的线性空间这一核心概念，及基于此概念上建立的新知识，是全新的且高度抽象，颇具现代数学思想的内容，这契合阶平班定位[11]。因此，以线性空间为主线设置教学内容是可行的。在本科阶段第一学期设置48 学时线性代数课程，开展以线性空间系列知识群为主要内容的尝试，是对线性代数课程教学与学习的挑战。概念抽象、计算偏少、逻辑推演较多、习题例题较少是其特点。根据阶平班基础课教学要求，注重独立思考及逻辑推理，推行部分基础内容通过自学习得，减少习题训练，课上教师只讲授重难点、预留师生互动环节，加强拓展性问题思考与解答，课下全方位全时段采用线上（微信）和线下面对面方式，针对学生感兴趣的问题和疑惑进行讨论、答疑互动。因此，以线性空间为主线的教学内容设置和相应的教学方法改革与阶平班的教学要求是契合的。

2.2 以线性空间为主线设置教学内容的策略

结合阶平班学生的实际状况，探索一条以线性空间为主线的线性代数课程体系、并在有限时间内完成教学实践是一种挑战。本研究采取的教学内容设置策略主要考虑了以下两方面：（1）涵盖目前线性代数课程的基本内容。根据教学大纲，按照课程目标将教学内容分为包含重难点的讲授内容、包含一般知识点和计算技能的学生自学内容以及课下探索延伸性内容三个层面。例如向量、矩阵代数运算、线性方程组的求解等为自学内容，线性空间、向量线性关系、基底与坐标、线性变换及其矩阵表示等为讲授内容，将矩阵的有关应用作为探索延伸性内容。（2）注重线性空间系列知识群的展开，适当植入重要知识点。首先，注重线性空间概念的发展及系列概念的内在逻辑[12]。从直观的三维几何空间出发，依据几何向量的运算及关系、坐标向量等发展一般线性空间，由向量的线性关系到线性空间的基底与维数；由几何空间中几何向量的长度、夹角，到内积及欧氏空间；标准正交基构建，由基底与基底的关系以及几何上点与点之间运动，引出线性映射与线性变换理论；基于线性变换理论，给出矩阵空间理论。其次，为深入理解概念，重视概念与基本结论的几何意义。线性代数课程的一个突出特点是定义定理的抽象性，借助定义定理的几何意义，能够帮助学生更好地理解定义定理的内涵。如图1 所示，如何定量描述线性变换对空间给定区域面积的影响？这便是行列式所能解决的，由此承上启下自然引出行列式理论。在给出三阶行列式的定义时，结合三阶行列式的几何意义如图2 所示，三维空间中以行向量张成空间中的平行六面体的体积，更好地帮助学生理解三阶行列式的定义。

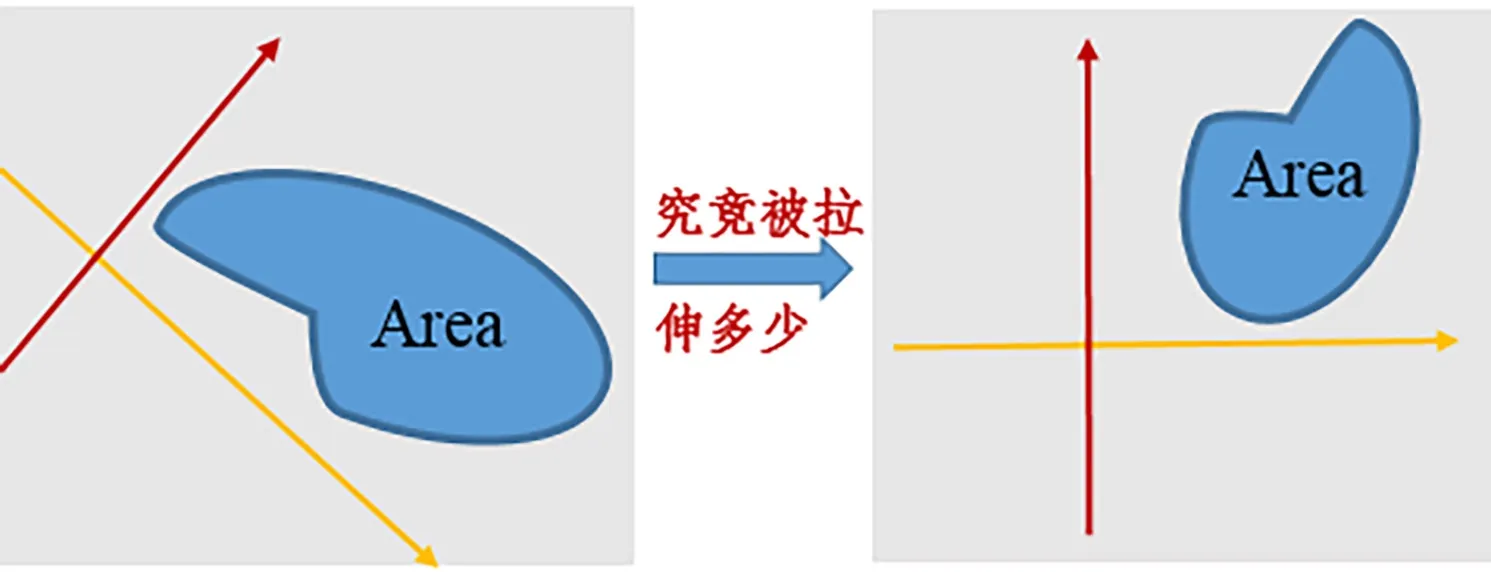
图1 线性变换对空间给定区域面积的影响Figure 1. Influence of linear transformation on the area of a given region of space

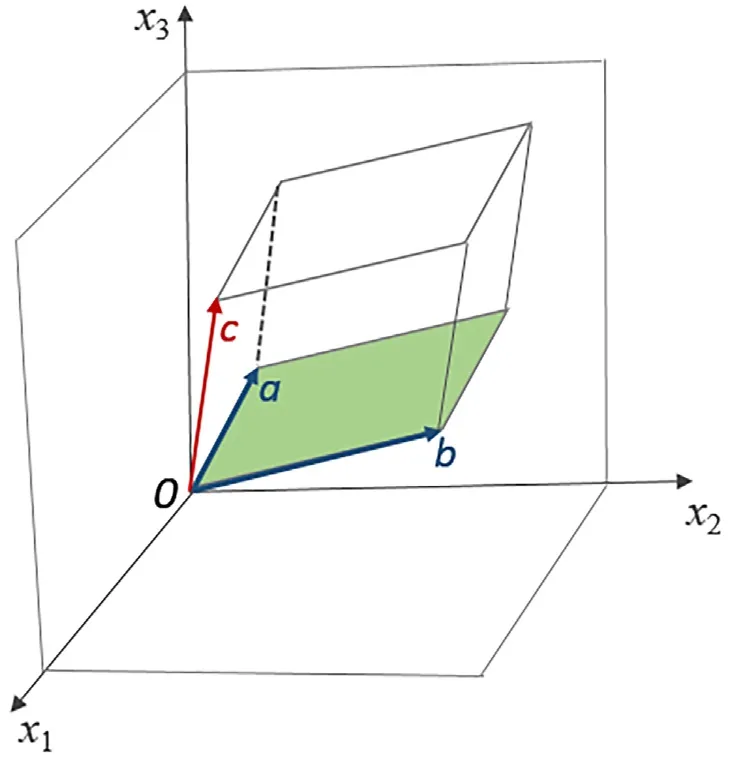
图2 三阶行列式几何意义Figure 2. Geometric significance of third-order determinants

3 以线性空间为主线进行教学内容改革的实践

本研究以首都医科大学临床医学及临床口腔专业阶平班为载体开展教学实践，采用课堂教师授课和课下学生自学相结合的形式完成了两轮教学过程。

基于讲授的知识点，教师提前给学生提供课前预习提纲和相关问题，使学生带着问题进入课堂，提高学生自主学习的能力。例如，对矩阵的初等变换知识点，设置“线性变换在一组基下可以用一个矩阵来表示，那么矩阵的初等变换对应于线性变换的什么呢？它要解决的是什么问题？”；对线性方程组的求解这个知识点，设置“线性方程组的常数项为零是齐次方程组，不为零就不是齐次方程组，如何理解齐次这个概念？”。

为解决概念的高度抽象性问题，在课堂教学过程中注重讲解概念的几何意义，强调具体背景、具体实例引出抽象的概念。例如，在讲授特征值理论时，先设置一个抛砖引玉问题：“如果矩阵对某一个向量或某些向量只发生伸缩变换而不产生旋转的效果，会是什么情况、有什么意义？”，引导学生从矩阵的可逆性、秩及初等变换的结果等矩阵的代数性质进行思考，过渡到“矩阵的几何特性会是什么？”，从而引出特征值与特征向量概念Ax=λx，并结合几何意义帮助学生更好地理解和掌握该概念，进一步通过图片压缩具体实例阐述特征值与特征向量在图像处理方面的应用。

在教学中提出探索延伸性问题。例如，作为代数求解特征值和特征向量问题的延伸，提出探索延伸性问题：“Householder 变换原理及其在特征值计算中的应用”。学生利用课后时间，通过文献学习形成研究性报告，进一步加深对特征值和特征向量的理解。

将课堂教学与课后全时段全方位的讨论、答疑互动融合为阶平班线性代数教学新模式。各班建立交流学习群，学生可以随时就学习中的问题在群里展开讨论，老师也可以给出提示由学生解答，在这个过程中学生探索新知识、解决问题的能力可以得到很大提升。

4 课程学习效果评价

对于课程学习效果的评价，强调以学生为中心，重视过程性考核[13]。研究人员在期末对临床医学及临床口腔专业阶平班2022 级线性代数教学班的49 名同学进行问卷调查，问卷包括20 个条目，其中12 个条目为单选题，8 个条目为多选题，内容涉及课前预习情况、课后自主学习情况、教学内容设置的难易程度、结构性学习方式的设置比例、课程学习效果及对引入探索性问题形成研究报告的可行性等。

共发放49 份问卷，回收率100%。调查结果见表1，对于教学内容设置的难易程度，10.20%的同学表示全部能理解，26.53%的同学表示大部分能理解，只有18.37%的同学表示对大部分内容不能理解；53.06%的同学认为引入探索性问题形成研究报告对教学效果非常有帮助，36.74%的同学认为比较有帮助；对于每周课后用于复习和自主学习的时间，超过6 小时的占4.08%，5～6小时的占2.04%，3～4 小时的占48.98%，1～2 小时的占44.90%。

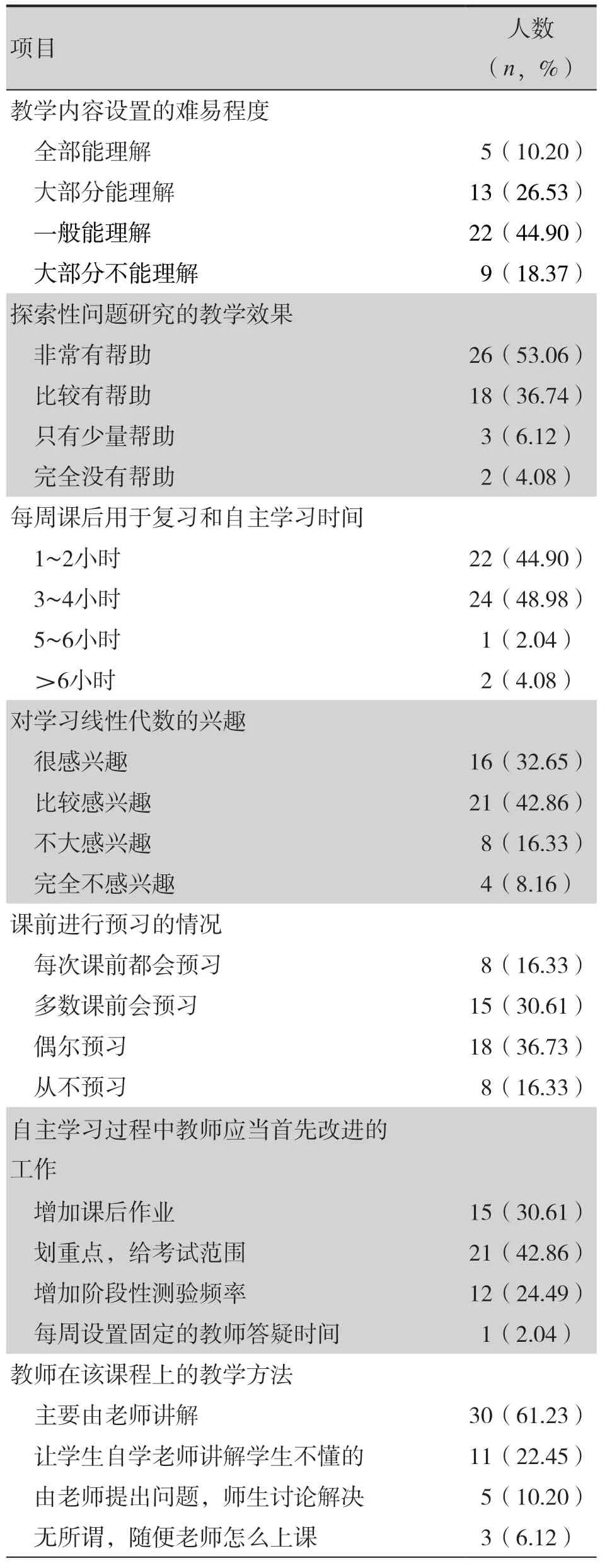
表1 教学效果问卷调查结果（n=49）Table 1. Results of questionnaire survey on teaching effect (n=49)

5 结语

本研究基于高端复合人才培养目标，对线性代数课程教学模式的改革进行探索，并开展相关教学实践，从课程定位的确立、教学大纲的制定、教学方案的设计，到具体的教学实践，积累了一些经验，取得了一定成效，可为构建符合培养目标需求的人才培养体系提供借鉴。

在全面推进“新工科”“新医科”建设和课程思政的背景下，在信息技术持续深入到教学全过程的形势下，基础课程教学内容、教学模式与考核方法面临全新的挑战。在教学实践中，强化“引学”“导学”，将课堂由“老师讲授”转变为“同学提问+教师解答的互动”，将课下被动做题转变为注重调动学生自主获取知识与技能的能动性、综合培养学生的创新、思辨和语言能力的自学、师-生与生-生之间的互动，将基本计算能力训练与相关计算软件操作技能融合起来，将传统单一的闭卷考试转变为形式多样的考核评价方法，还有许多教学课题亟待持续研究与实践。