基于EBF神经网络的引射器结构参数优化
2023-12-04么大锁赵凯芳吴国鹏季宁裴毅强
么大锁,赵凯芳,吴国鹏,季宁,裴毅强
(1.天津仁爱学院机械工程学院,天津 301636;2.天津大学内燃机燃烧学国家重点实验室,天津 300072;3.天津仁爱学院数学教学部,天津 301636)
0 前言
氢能是一种理想的清洁能源,已成为研究和发展热点[1]。发展氢能和氢燃料电池具有巨大的能源战略意义。《中国制造2025》明确提出燃料电池汽车发展规划,更是将发展氢燃料电池提升到了战略高度[2]。由于引射器没有运动部件,具有结构简单、运行可靠且无额外功耗等优点,逐渐在燃料电池氢循环系统中得到广泛应用[3-4]。然而引射器的工作性能受流体压力、尺寸结构等多种因素影响,且存在强烈的非线性、流固耦合问题,因此,如何实现引射器的高效运作和优化设计是当前亟需解决的重要技术问题[5]。
南泽群等[6]提出在未来高性能燃料电池系统中,应通过优化引射器的结构,提高引射性能。张家明等[7]提出了引射器与氢循环泵并联的大功率氢气循环系统方案,解决了引射器低工况引射效果不佳的问题。纪少波等[8]对可调式引射器进行了研究,通过数值模拟方法研究了部分结构尺寸对可调式引射器性能的影响。尹燕等人[9]基于CFD方法,探索了结构参数和操作条件对引射器性能的影响。张心悦等[10]采用计算流体力学和实验相结合的方法,获取多组不同喷嘴距和工况条件下引射器内部压力场和速度场,研究了变工况下喷嘴距对引射器性能的影响的演变规律。WANG等[11]采用Fluent对引射器不同扩散室角度对引射系数的影响进行了研究,结果表明:当引射器在其额定功率80 kW下工作时,扩散室角度为11°时,引射器的引射系数最高。BAI等[12]提出有关Proton Exchange Membrane Fuel Cell(PEMFC)氢气循环系统中收敛式喷嘴引射器几何参数的优化方法,并基于混合人工鱼群算法对引射器的几何参数进行优化。PEI等[13]考虑燃料电池的阳极压降特性建立了计算流体动力学模型,并对引射器进行了结构优化和工作性能分析,提高了引射器在低负载工况下的性能。MAGHSOODI等[14]和BRUNNER等[15]使用二维CFD模型对引射器尺寸进行了模拟优化。EXPASITO CARRILLO等[16]运用代理模型和遗传算法对应用于CO2制冷系统中的引射器结构参数进行了优化研究。山东大学和西安交通大学的学者,为提高引射器的适用功率范围,研究了多喷嘴引射器对燃料电池系统的影响[17-18]。
由于三维CFD模拟计算时间长,学者们更多应用二维CFD模型开展了引射性能的仿真或实验研究,或运用三维CFD模型和单因素变量法研究了部分结构参数对引射系数的影响,试验次数有限。鲜见运用科学的试验设计方法对燃料电池引射器结构参数进行全局寻优的研究。
无论采用引射器和循环泵并联,还是采用单引射器或双引射器作为燃料电池的氢循环装置,都需要高性能的引射器,因此,对引射器进行结构参数优化研究具有重要意义。以额定工况下氢燃料电池引射器为研究对象,建立引射器三维CFD模型,提出一种基于EBF(Ellipsoidal Basis Function)神经网络模型和NLPQL(Non-linear Programming by Quadratic Lagrangian)算法的引射器结构参数优化方法。基于正交试验设计,建立了EBF神经网络模型描述引射器结构参数与引射系数间的非线性关系,采用最优拉丁超立方设计获得样本点,通过引射系数模拟值与代理模型预测值的对比和复相关系数,验证了代理模型精度,应用NLPQL算法进行全局寻优,获得了使引射系数最大的结构参数组合,并进行模拟验证。
1 引射器工作原理及优化目标
1.1 工作原理
为维持氢燃料电池的正常工作,需要提供过量氢气,而回收未反应的氢气可以提高燃料电池的效率。因此,氢气循环系统对提高燃料电池效率具有重要意义。应用引射器作为氢气循环装置的燃料电池氢气循环系统如图1 所示。

图1 燃料电池氢气循环系统Fig.1 Fuel cell hydrogen circulation system
引射器的结构组成及尺寸参数如图2所示。
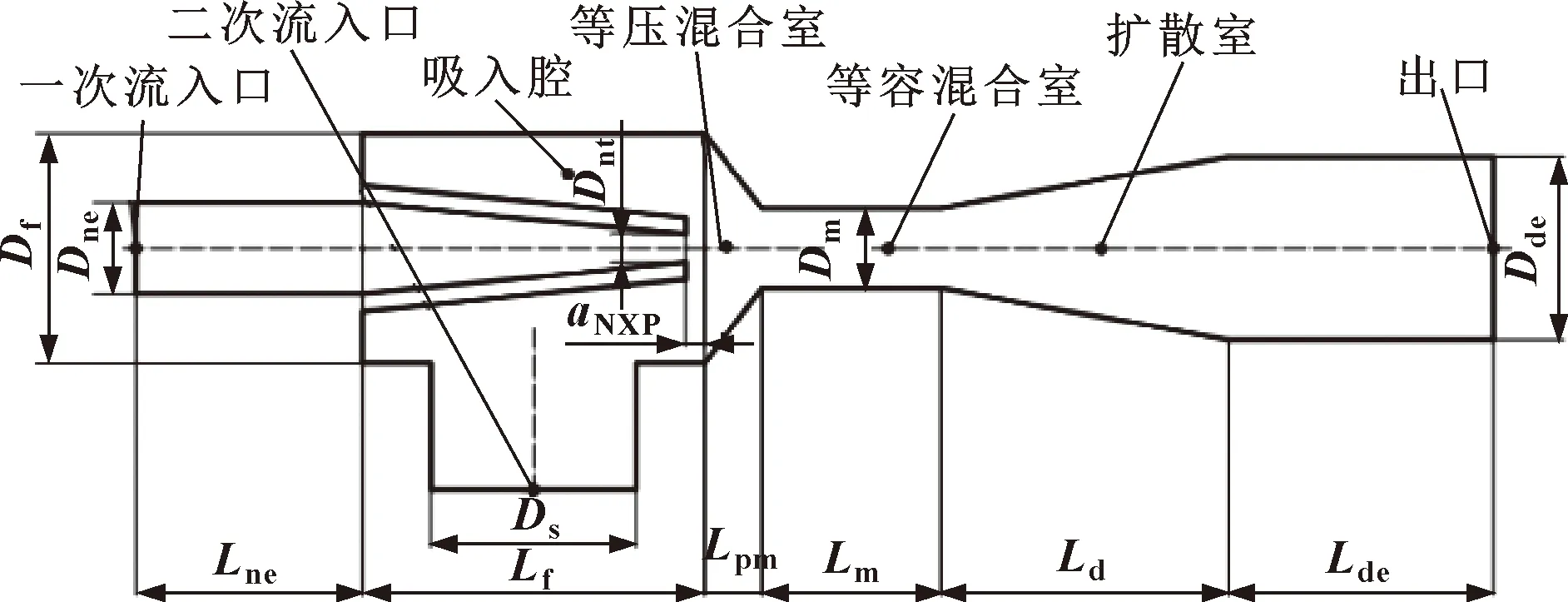
图2 引射器结构组成及尺寸参数Fig.2 Structure composition and size parameters of ejector
在氢燃料电池工作过程中,高压氢气经过压力调节器和质量流量计后进入引射器一次流入口,氢气由喷嘴喷出后,速度增大,压力降低,使吸入腔的压力低于二次流入口,二次流被吸进来并同一次进流混合,其中二次流入口被吸入的是未反应完的氢气与水蒸气的混合物。混合后的气体速度逐渐降低,压力逐渐升高,逐渐达到燃料电池的工作压力。
1.2 优化目标
引射器的性能由引射系数来评估,引射系数直接反映了引射器引射二次流的能力,引射系数越大表明引射器的性能越好。引射系数的计算式为
ω=ms/mp
(1)
式中:ms和mp分别为二次流体和一次流体的质量流量,ms由Fluent求解获得。
引射系数表征引射器的工作性能,并作为引射器结构参数优化的目标。在一次流质量流量不变的情况下,引射系数越大表明引射器的性能越好。
2 建立引射器CFD分析模型
2.1 建立引射器流体计算域
根据文献[19]中已知的80 kW氢燃料电池引射器结构参数及分析结果,选取对引射器性能影响较大的6个结构参数作为研究对象,每个参数设置5个水平。其中,aNXP为负值表示喷嘴位置在吸入腔内,aNXP为正值表示喷嘴位置在吸入腔外,引射器结构参数及水平如表1所示。
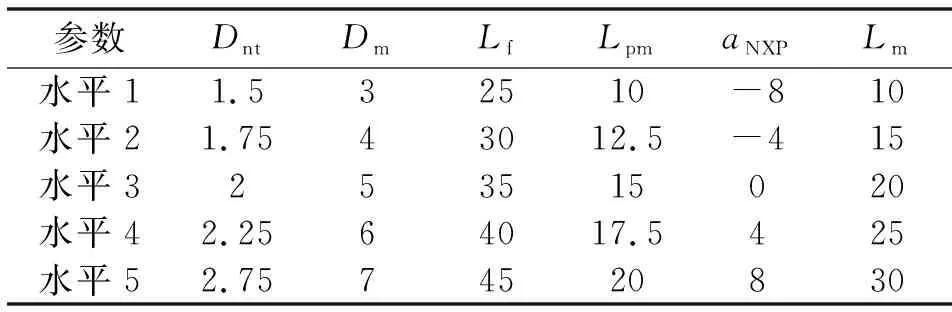
表1 引射器结构参数及水平 单位:mmTab.1 Structural parameters and level of ejector Unit:mm
建立引射器三维模型导入到ICEM软件中建立引射器三维CFD模拟仿真计算域,并划分网格,不同尺寸的引射器网格数量在(280~400)万左右,最小单元尺寸0.5 mm。经网格无关性检验,排除了网格大小和数量对计算结果的影响,引射器三维CFD分析模型如图3所示。
2.2 控制方程
假设引射器内部流体为稳定、湍流和可压缩流体。在忽略了蒸汽冷凝以及重力影响的条件下,根据牛顿流体流动守恒方程,建立了引射器内部流动控制方程,即质量、动量、能量的守恒方程[10]。
质量守恒方程
(2)
其中:ui和ρ分别为第i个方向的速度和密度。
动量守恒方程
(3)
其中:P和σ分别为压力和应力张量。
能量守恒方程
(4)
(5)
其中:E为总能量;k为有效导热系数;hi和Ji分别是焓和扩散量;δij为克罗内克符号。
2.3 边界条件及求解方法
引射器一次流入口采用质量流量边界,二次流入口和出口均设置为压力边界。针对80 kW氢燃料电池,确定引射器工作的边界条件,如表2所示。
为解决CFD模拟仿真时间长的问题,应用多台计算机进行求解。湍流模型采用 RNGκ-ε模型。每个算例,计算2 000步后,各个参数残差值达10-4数量级,二次回流流量保持稳定,并且两个入口流量之和与出口流量的差值小于1×10-6时认为计算收敛。
3 建立EBF神经网络模型
引射器结构参数对引射系数的影响是多参数综合作用的结果,单因素变量法存在局限性。
基于代理模型进行优化设计的优势在于获得输入、输出变量之间的函数关系;减少耗时的仿真程序调用,提高优化效率;通常可将实际求解时间缩短几个数量级[20]。
3.1 正交试验设计及结果
正交试验设计是安排多因素多水平试验、寻求最优水平组合的一种高效率试验设计方法,既能使试验点分布得很均匀,又能减少试验次数,并得出最优水平组合[21]。
以表1中引射器的6个结构参数作为正交试验的因素,查正交试验表L25(56),需要25次试验,如果采用全面试验需要56次试验,大大减少了试验次数。通过模拟仿真计算引射系数,正交试验设计及结果如表3所示。
正交试验虽然能进行单目标优化,获得最优水平组合,但由于样本点数据不是连续的,只能得到现有水平的最佳组合,并不能预测最大引射系数获得全局最优解。代理模型的意义在于能够找到全局最优点,并预测最大引射系数,提高优化效率。
3.2 EBF神经网络模型
EBF神经网络模型具有很强的逼近复杂非线性函数的能力;无须数学假设,具有黑箱特点;学习速度快,具有极好的泛化能力;较强的容错功能,即使样本中含有“噪声”输入,也不影响网络的整体性能。
EBF神经网络模型是含有隐层的 3 层前馈神经网络,其中输入层主要负责接收输入变量,隐层负责对输入变量进行非线性变换,输出层负责输出变量,网络的最终输出是由几个隐节点的线性加权和得到的。神经网络的数学表达式为
(6)
式中:X为输入变量;N为隐节点数目;αj为隐节点对应的一组输出权值;αN+1为未知偏差值;gj(X)为高斯基函数。
EBF神经网络模型使用全协方差矩阵代替径向基神经网络中的对角型协方差矩阵,显著提高了网络分类能力。EBF模型以样本点与隐节点中心之间的Mahalanobis距离作为自变量,以高斯函数作为基函数,其表达式[22]为
(7)
(8)
其中:cj为隐节点中心值;Sj为全协方差矩阵,近似等于样本方差。
将25组试验数据中6个试验因素作为神经网络的输入层,引射系数作为输出层,构建EBF神经网络映射模型。
3.3 EBF神经网络模型精度检验
为检验EBF神经网络模型的准确性,运用最优拉丁超立方试验设计方法,在试验因素取值范围内重新选取10组数据进行试验设计,并计算引射系数。最优拉丁超立方设计使所有的试验点尽量均匀地分布在设计空间,具有非常好的空间填充性和均衡性。最优拉丁超立方试验方案及结果如表4所示。
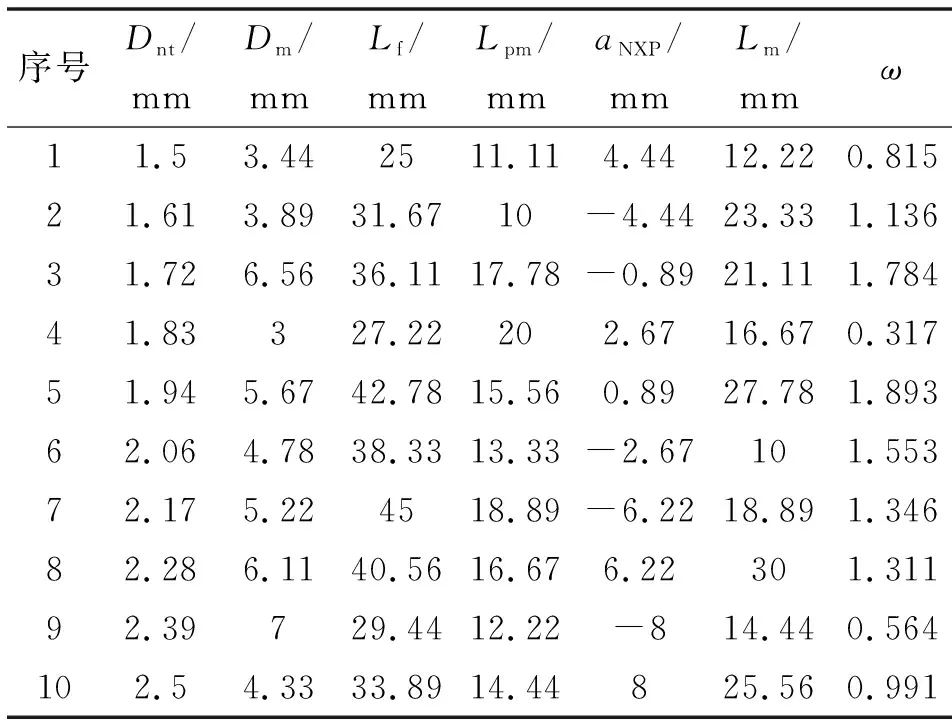
表4 最优拉丁超立方试验方案及结果Tab.4 The optimal Latine hypercube experiment scheme and results
如表4所示,运用10组试验结果对训练完成的EBF神经网络进行检验,神经网络预测值与模拟结果对比如图4所示。
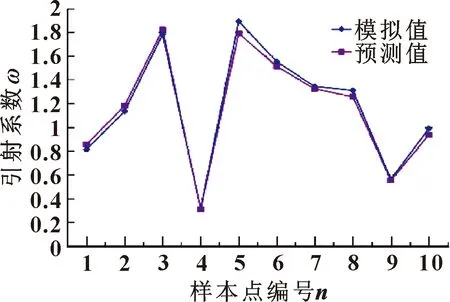
图4 预测值与模拟结果对比Fig.4 Comparison between predicted values and simulation results
由图4可知:神经网络预测值与模拟值最大误差为5.65%。证明EBF神经网络预测值与软件模拟值误差较小,可以使用神经网路模型代替有限元分析模型。
神经网络模型精度还可以使用复相关系数R2来评价。R2值表示预测值与模拟值之间的相似度,反映了神经网络模型预测值与模拟值的符合程度[23]。其计算方法为
(9)
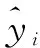
R2∈[0,1],R2越接近于1,表示神经网络模型预测结果越准确,一般要求R2>0.9。经计算,模型复相关系数为0.953,模型精度满足要求。
通过模拟值与预测值的对比和复相关系数验证,EBF神经网络模型能够准确地预测引射系数,因此,可以使用EBF神经网络代替CFD模拟仿真,优化引射器结构参数,寻求最大引射系数。
4 基于NLPQL算法的结构参数优化
NLPQL算法应用二次泰勒级数将目标函数展开并且将约束条件线性化,将原非线性问题转化为二次规划问题。NLPQL算法利用类牛顿矩阵Bk定义了一个拉格朗日函数L(x,u)的二阶逼近和一个L(xk,uk)的海森(Hessian)矩阵的逼近,于是得到一个二次序列规划的子问题[24]。
(10)
其中:d为搜索方向;Bk为类牛顿矩阵;f(xk)为目标函数;∇f(xk)为目标函数的梯度;gq(xk)为约束函数;∇gq(xk)为约束函数的梯度;xl为边界约束的下限;xu为约束边界的上限;q为变量,q={1,2,…,me,me+1,me+2,…,m}。
经过迭代寻优,得到引射系数的最大值为2.441,对应的引射器最优结构方案如表5所示。
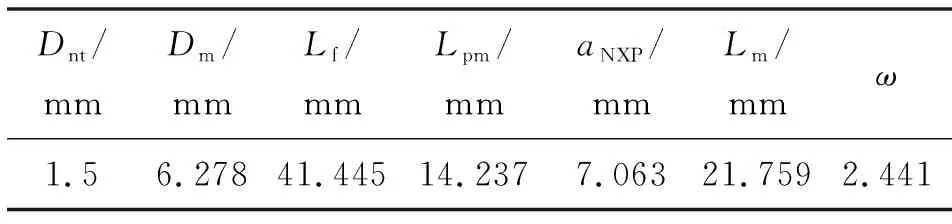
表5 引射器最优结构方案Tab.5 Optimal structure scheme of ejector
5 模拟验证
使用优化后的引射器最优结构方案建立CFD模拟仿真计算域,用Fluent进行求解,监测一次流入口流量、二次流入口流量、出口流量,引射器质量流量如图5所示。
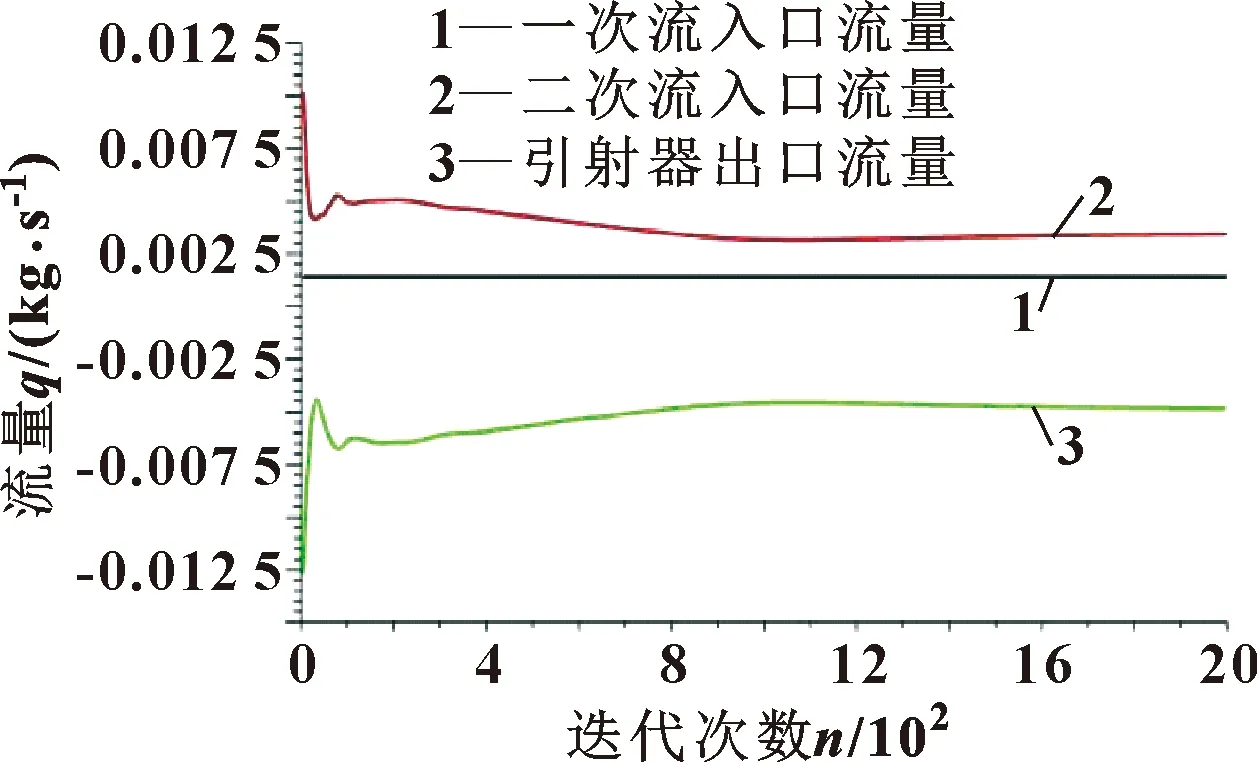
图5 引射器质量流量Fig.5 Mass flow of ejector
经计算,引射比为2.454,相对于正交试验方案的最大值提高了3.9%,达到了优化引射器性能的目的。
6 结论
(1)基于EBF神经网络和CFD模拟仿真技术,建立了引射器结构参数与引射器系数间的神经网络模型;通过模拟值与预测值的对比以及复相关系数,验证了神经网络模型的精度,说明EBF神经网络模型能够准确地预测引射系数。因此,可以使用EBF神经网络代替CFD模拟仿真,优化引射器结构参数,寻求最大引射系数。
(2)应用NLPQL算法和EBF神经网络模型进行全局寻优,获得了使引射系数最大的结构参数组合,并进行模拟验证。研究结果表明:基于EBF神经网络和NLPQL算法,提高了燃料电池引射器的引射系数,相对于正交试验方案的最大值提高了3.9%,优化了引射器结构。
(3)相对于运用单因素变量法研究结构参数对引射器性能的影响,基于正交试验设计和EBF神经网络的方法,可以扩大结构参数研究范围和水平,节约CFD模拟计算时间,对引射器结构参数的优化研究具有指导和借鉴意义。
