人体下肢多关节连续运动的肌电预测方法
2023-12-04韩永林陶庆张小栋陈清正
韩永林 ,陶庆,张小栋,陈清正
(1.新疆大学机械工程学院,新疆乌鲁木齐 830047;2.西安交通大学机械工程学院,陕西西安 710049)
0 前言
随着人机交互技术的发展,下肢外骨骼康复机器人[1]、下肢助力外骨骼机器人[2]及智能假肢[3]等康复设备已成为目前研究的热点。生物电信号因其检测方便、无创、反应超前等特点,成为人机交互领域的主流研究对象[4-5]。表面肌电信号(surface Electromyography,sEMG)是人体产生肌肉电活动的记录,比脑电信号更加稳定,在运动控制和神经肌肉生理等方面有着广泛的应用[6-8]。
目前,国内外学者已经做了不少利用表面肌电信号进行动作分类[9-10]和连续运动量预测[11-12]的研究。第一种方法,研究人员利用表面肌电信号来识别人体肢体的不同运动模式,研究的目的是获得更高的识别率和更多的运动模式,特征提取方法和分类算法是研究的重点[13]。然而,只能识别有限的运动模式,作为机器人的开关信号,严重影响了机器人的协调性和流畅性。相比之下,利用表面肌电信号(sEMG)进行连续运动预测可解决这个问题,提高康复设备的人机协调性能和流畅性。预测连续运动量变化是康复机器人领域实现智能肢体平滑控制的关键,因此连续运动角度预测有着广阔的应用前景[14-15]。
目前利用肌电信号的连续运动预测方法主要集中在生物力学模型[16-17]和神经网络回归模型[18-19]上。基于生物力学模型的系统包括运动学模型、动态模型和肌肉骨骼模型。Hill肌肉模型是应用最广泛的。BUCHANAN等[20]建立了前向神经肌肉骨骼Hill模型。在该模型中,首先将sEMG信号转化为肌肉激活值,再根据肌肉收缩动力学将肌肉激活值转化为肌肉力量;然后,建立骨骼肌的几何模型,将肌肉力转化为关节扭矩;最后,通过关节扭矩预测关节运动。HAN等[21]提出一种肌电状态空间模型来预测关节角度。该模型基于Hill肌肉模型和前向动力学,利用运动变量表示神经激活,提取sEMG的绝对值积分和波长特征,构建运动变量与sEMG特征的二次方程来预测关节角度;最后,他们将该方法与传统方法进行了比较,以验证模型的准确性。XI 等[12]提出一种表面肌电(sEMG)状态空间模型,用于根据sEMG信号估计连续的下肢关节运动,该模型将前向动力学与基于希尔的肌肉模型(HMM)相结合,使扩展模型能够直接估计下肢关节运动。
虽然上述模型对单关节运动回归实现了很好的拟合,但大量难以测量的生理参数使得模型难以训练。此外,在对具有多自由度的多个关节进行建模时,人体肌肉的冗余控制使得模型非常复杂。与生理肌肉模型相比,神经网络模型是更直接、方便的方法。神经网络强大的拟合能力使得利用肌电信号进行连续性控制成为可能。华中科技大学张琴等人[22]通过支持向量机对下肢多关节角度进行连续运动肌电预测,通过RMSE评价,3个关节的误差分别为9.36°、10.82°和6.87°。西安交通大学陈江城、张小栋[23]基于受限玻尔兹曼机构建立深度自动编码器,配合BP神经网络,精确估计下肢关节的连续运动,误差较传统方法降低了25%~35%。CHERON等[24]采集下肢6块肌肉的sEMG,构建动态递归神经网络(Dynamic Recurrent Neural Network,DRNN)预测模型来估计下肢关节角度,分析了DRNN的学习规则、隐藏层节点数和训练次数对预测结果的影响;实验结果表明,在选择正确的参数时,DRNN可用于预测多个sEMG信号与关节运动之间的关系。
为了使下肢外骨骼康复机器人、下肢助力外骨骼机器人及智能假肢等康复设备,在适应不同运动模式下的康复训练和辅助行走时,能够提供更好的仿生模式和适应能力,本文作者将以人体蹲起运动、膝屈伸运动和上下阶梯运动为例,提出一种麻雀搜索算法优化Elman神经网络预测模型,并利用下肢肌电信号进行踝、膝和髋关节连续运动预测,最后通过6位受试者的统计分析来验证所提方法的有效性。
1 下肢多关节连续运动的表面肌电与轨迹获取方法
此研究主要包括人体下肢多关节连续运动的表面肌电、运动特征数据获取,以及基于运动特征参数的下肢多关节运动曲线反求模拟。首先,开展大量的人体运动实验,获取所需肌电和运动数据,进行相应的数据处理;然后,基于运动数据反求关节轨迹曲线。
1.1 获取系统设置与实验范式
如图1所示,此研究采用的动作捕捉系统(VICON,Oxford Metrics Limited,UK)主要由MX-cameras、MX-Giganet和带有NEXUS软件的主机PC组成。其中的10个摄像头主要用来收集放置在下肢表面的16个运动捕捉标记的运动数据,且采样频率设定为100 Hz;MX-Giganet连接主机PC和MX相机,提供VICON和EMG系统之间的接口,并允许同步记录运动学和EMG数据。肌电信号使用Noraxon无线表面肌电采集设备进行采集,肌电信号采样频率为2 000 Hz。

图1 实验场景Fig.1 Experiment scene
实验征集了6名平均年龄为(23±1.5)岁,体质量48~100 kg,身高158~180 cm的健康受试者进行数据采集实验,受试者分别进行下肢蹲起运动实验、膝屈伸运动实验和上下阶梯运动实验。
在下肢蹲起运动实验中,受试者在自然状态下蹲起10次为一组数据,每人采集4组数据;在膝屈伸运动实验中,受试者在自然状态下膝关节屈伸往复10次为一组数据,每人采集3组数据;在上下阶梯运动实验中,受试者完成一次上下阶梯为一组数据,每人采集8组数据。
1.2 肌电信号的获取与处理
1.2.1 测点布置
人体单侧下肢至少包含30块肌肉,驱动下肢7个自由度运动。为了更好地获取人体下肢肌电信号,选取了7块与人体下肢运动联系密切的肌肉,分别为股直肌、胫骨前肌、比目鱼肌、腓肠肌、股内侧肌、股外侧肌、股二头肌,如图2所示。放置7个传感器于下肢7块肌肉对应的位置。
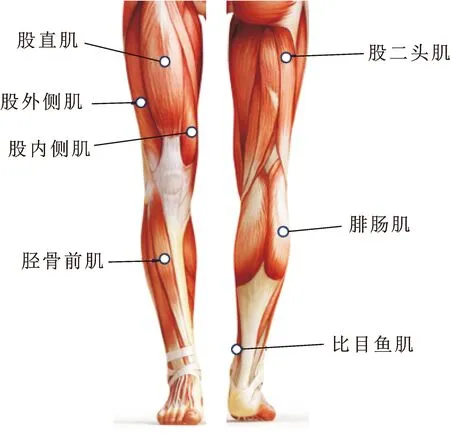
图2 人体下肢肌肉分布Fig.2 Muscle distribution of human lower limbs
1.2.2 信号处理方法
肌电信号的处理过程包括两个部分:首先,经过滤波处理以消除噪声;然后,提取各个通道的特征信号,作为模型的输入值。
(1)去噪处理。肌电信号是一种复杂的微弱低频生物电信号,在测量过程中容易受到其他因素的干扰。在对肌电信号进行特征提取之前,需要滤除噪声以获得具有高信噪比的肌电信号。
肌电信号中存在3种主要类型的噪声:(1)第一类噪声是采集设备中电子元件的固有噪声;(2)第二种噪声是电力系统的工频干扰;(3)第三种噪声来源于电极、皮肤和放大器之间的相对运动,导致基线漂移。因此,通过肌电采集系统采集的肌电信号中存在大量噪声,其噪声源广泛。如果不对这些噪声进行预测和处理,建立预测模型的特征提取,将导致预期的关节角度和实际的关节角度之间有很大的不同。
实验将采集到的原始肌电数据,使用了一组滤波器,包括一个sgolay滤波器消除趋势化,一个带通滤波器(4阶巴特沃斯,20~200 Hz)来去除低/高频噪声,以及一个陷波滤波器(50 Hz)来去除电源频率信号。
(2)特征提取。滤波后的肌电信号包含冗余信息,信号区分度不高。因此,有必要对肌电信号进行特征提取。在获得肌电信号的时域和频域特征值之前,必须对肌电信号数据进行分割。常用的分割方法是加窗,包括静态分析窗和滑动分析窗。从图3可以看出,肌电信号可以根据滑动窗口W划分为不同的数据分析段。这些数据分析段的长度Wm相同。一般情况下,滑动窗口的长度Wm小于数据分析段的长度W。在这种情况下,表面肌电信号中的一些数据将被叠加。但是,如果滑动窗口的长度Wm大于数据分析段的长度W,就会丢失一些信号,很容易遗漏重要信息,所以一般不选择这种情况。在实际实验中,需要详细分析数据分析段的长度W和移动窗口的长度Wm。移动窗口越短,数据重叠越多,保证了数据的真实性,但是增加了计算复杂度。数据分析段越短,估计的数据段方差越大,需要综合考虑不同的特点。综合考虑,文中数据分析段长度为20,移动窗口长度为20,保证了肌电与运动数据长度一致,便于计算。

图3 滑动窗口示意Fig.3 Sliding window
肌电信号特征提取方法包括时域分析、频域分析、时频分析。为了降低计算复杂度,本文作者选取时域特征进行提取。均方根(RMS)值反映肌电信号电压幅值在时间维度上的变化(如图4所示)和相关肌肉力量的变化,所以RMS值是利用肌电信号进行连续运动预测中最具意义的特征值,如式(1)所示:
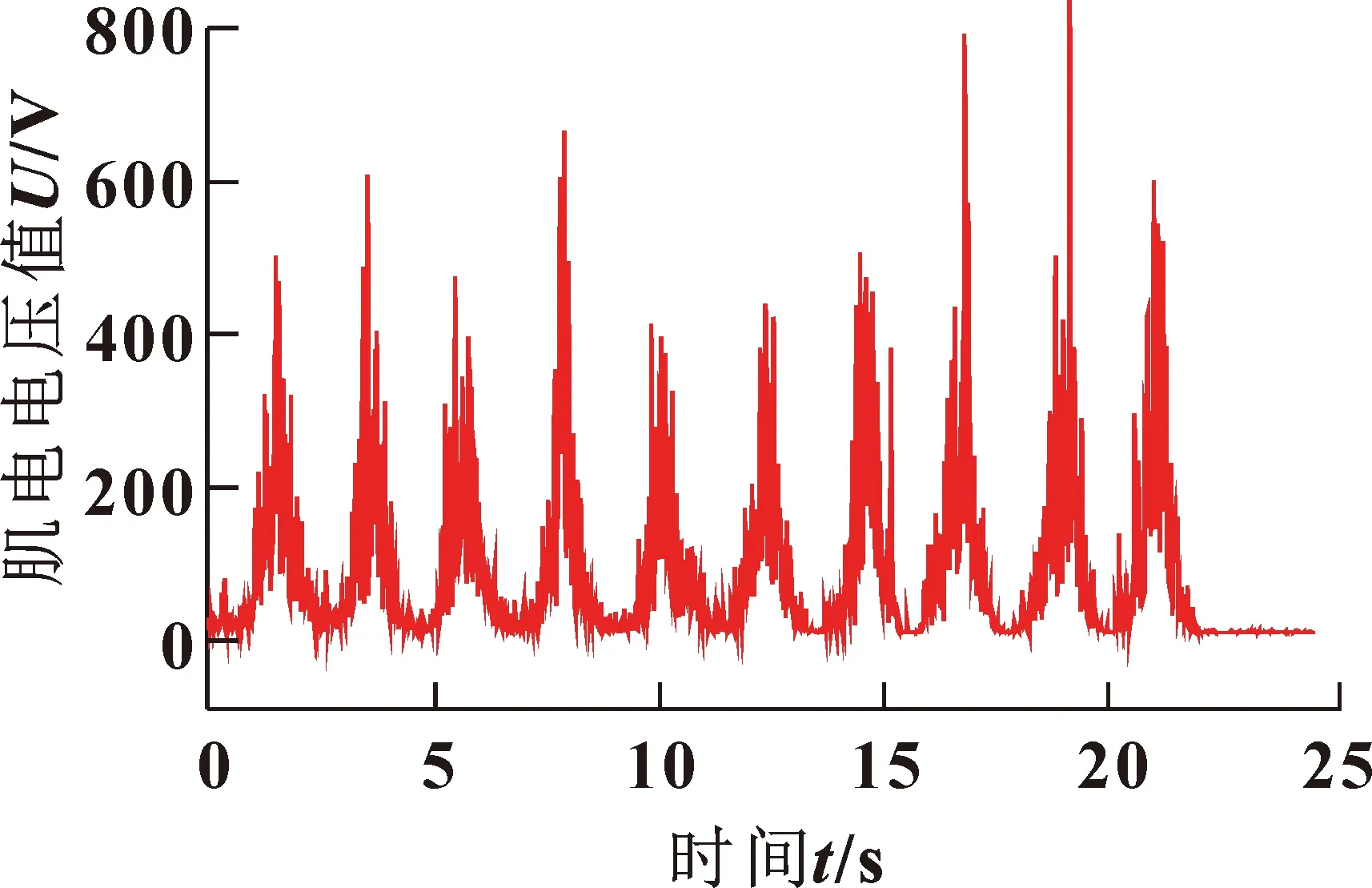
图4 肌电信号的RMS特征值Fig.4 RMS eigenvalue of EMG signal
(1)
式中:N是采样个数;xi是带通滤波器滤波后肌电信号的第i个采样点。
(3)预测样本设置。在运动预测阶段,分别从肌电特征值和运动数据中提取部分数据输入到模型中进行训练与测试。
其中,蹲起运动获得的肌电信号经特征提取后获得3 200个样本信号,选取前2 300个样本信号作为训练数据集,剩余900个样本信号作为测试数据集;膝屈伸运动获得的肌电信号经特征提取后获得1 850个样本信号,选取前1 050个样本信号作为训练数据集,剩余800个样本信号作为测试数据集;上下阶梯运动获得的肌电信号经特征提取后获得2 438个样本数据,选取前1 438个样本信号作为训练数据集,剩余1 000个样本信号作为测试数据集。
1.3 关节连续运动曲线反求模拟
正确计算出下肢关节角度是建立肌电-运动映射关系的必需条件,在这项工作中,使用标记的轨迹来计算关节角度。
肌肉骨骼几何建模软件Opensim用于将通用肌肉骨骼几何模型缩放到每个受试者,以根据静态姿势的实验测量标记位置匹配他们的人体测量学。在缩放过程中,根据实验标记的位置创建虚拟标记并将其放置在肌肉骨骼几何模型上,如图5所示。
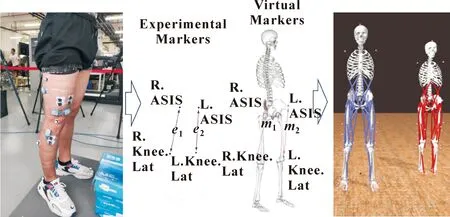
图5 个性化模型建立流程Fig.5 Flow for personalization modeling
人体模型建立以后,采用逆运动学算法获取人体运动中下肢关节角度变化,为人体运动特征分析做准备。Opensim逆运动学算法可以遍历整个运动过程,解决最小化标记误差的加权最小二乘优化问题,精度高,误差表示为
(2)
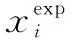
如图6和图7所示:Opensim逆向运动学得到的下肢关节运动曲线与余弦公式得到的下肢运动曲线运动趋势基本一致,虽然关节角度有一定变化,这可能由于模型缩放不准确或传统逆运动学分析忽略了其他影响因素,但是符合运动的一般规律,证实了Opensim仿真的有效性。
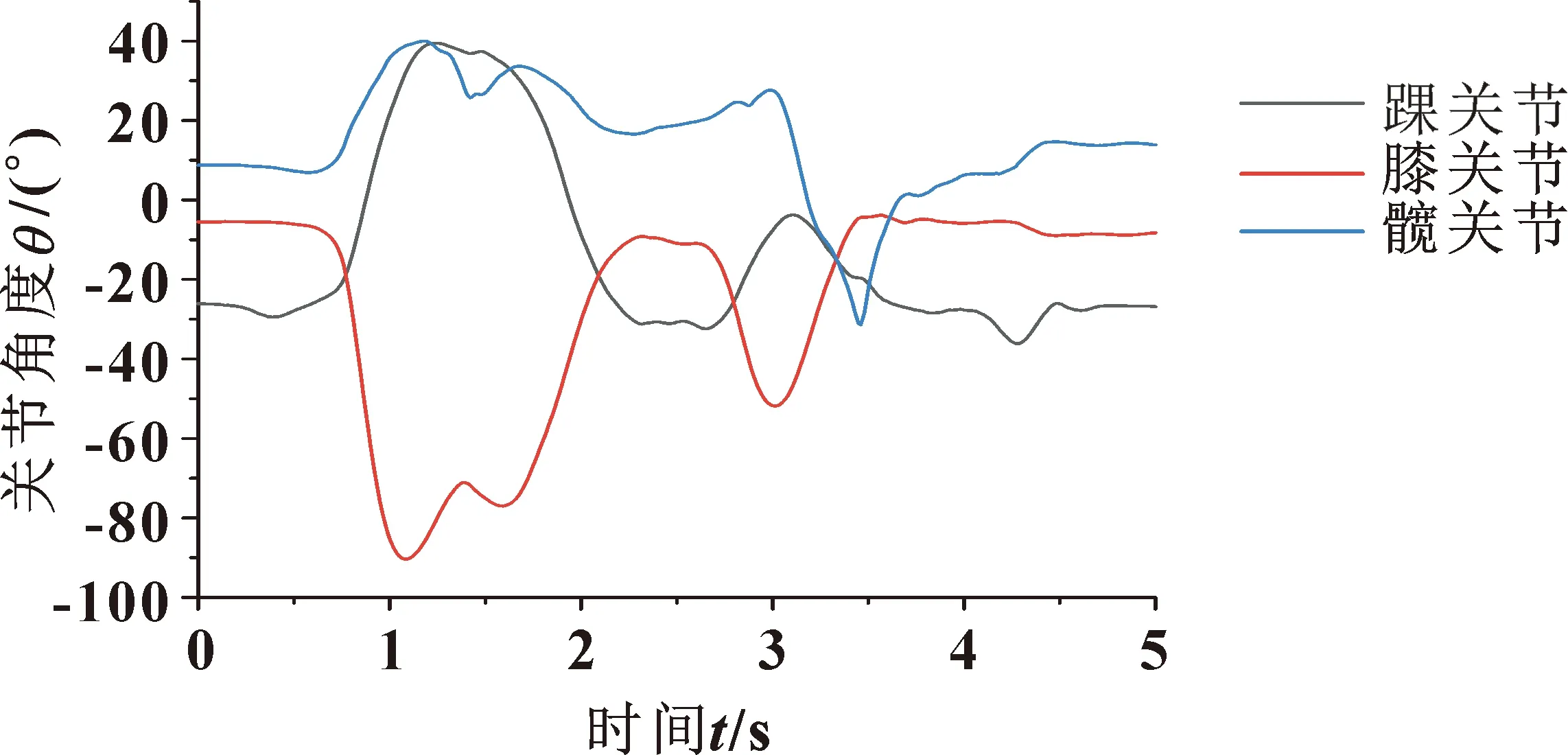
图6 Opensim逆向运动学得到的下肢关节曲线Fig.6 Curves of lower limb joints obtained by inverse kinematics in Opensim

图7 余弦公式计算出的下肢关节曲线Fig.7 Curves of lower limb joint calculated by cosine formula
2 多关节连续运动肌电预测方法
2.1 Elman神经网络模型设定
Elman神经网络具有良好的动态特性和较强的全局稳定性,在处理非线性、动态和复杂数据方面应用最为广泛。然而,作为反向传播(BP)神经网络的优化,Elman模型不可避免地继承了其固有的一些缺陷,例如存在容易陷入局部最小点和难以达到全局最优值的缺点。
Elman是一种动态循环网络。与传统的反向传播神经网络相比,它还有一个特殊的结构单元——承接层(如图8所示),用于存储隐含层在上一时刻的输出值,使得Elman网络具有学习时变模式的能力。因此,该网络在预测时间序列方面优于其他方法。
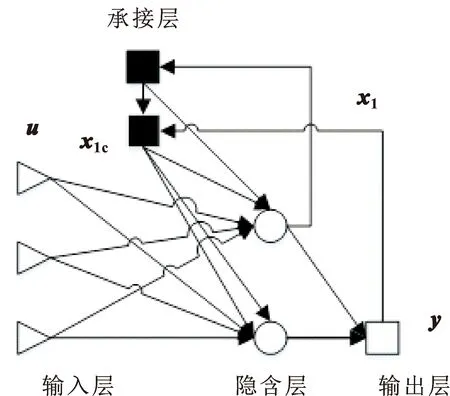
图8 Elman结构Fig.8 Elman structure
Elman神经网络的数学表达式为
y(k)=g[w2u(k)]
(3)
u(k)=f[w3uc(k)+w1x(k-1)]
(4)
uc(k)=u(k-1)
(5)
式中:w1、w2、w3分别是输入层到隐含层、隐含层到输出层和隐含层到承接层的连接权重;x是输入向量;y是输出向量;u是隐含层的输出向量;u(x)是反馈状态向量;f(x)是隐含层的传递函数;g(x)是输出层的传递函数,是隐含层输出的线性组合。
Elman神经网络采用标准BP网络算法来更新权值与阈值,其学习指标函数采用误差平方和函数,表达式为
E(k)=1/2[(yd(k)-y(k))T(yd(k)-y(k))]
(6)
式中:yd(k)为目标函数输出值。
为评价预测算法的准确性,采用均方根误差R和相关系数C对指标算法的预测结果进行评价。文中均方根误差用于估计预测值与实际值之间的偏差,相关系数显示了预测值与实际值之间的线性相关性,如公式(7)和(8)所示:
(7)
(8)

2.2 通用神经网络预测分析
通过以上数据处理,获得了肌电信号特征值和关节运动角度值,利用多种机器学习方法建立肌电-运动的映射关系,例如反向传播(Back Propagation,BP)神经网络、支持向量机回归(SVR)和Elman神经网络。
为了获得一种预测精度较好的模型,首先,从6名受试者蹲起运动实验数据的肌电特征值与关节角度值中选取前2 300个样本信号作为训练数据集,输入到模型中进行训练。最后,将剩余的900个样本信号作为测试数据集进行测试,并对膝关节的预测误差进行对比分析。
作者对单通道和多通道的肌电信号进行了验证分析,根据分析结果得出股直肌、胫骨前肌代表的两个通道的肌电信号在下肢预测方面表现较好,所以选择这两个通道的肌电信号来进行预测工作。
从表1中可见:Elman神经网络预测误差最小。由验证分析可知,少量通道的肌电信号不仅在实际应用更加方便、快捷,而且可以获得等同甚至更好的实验结果。
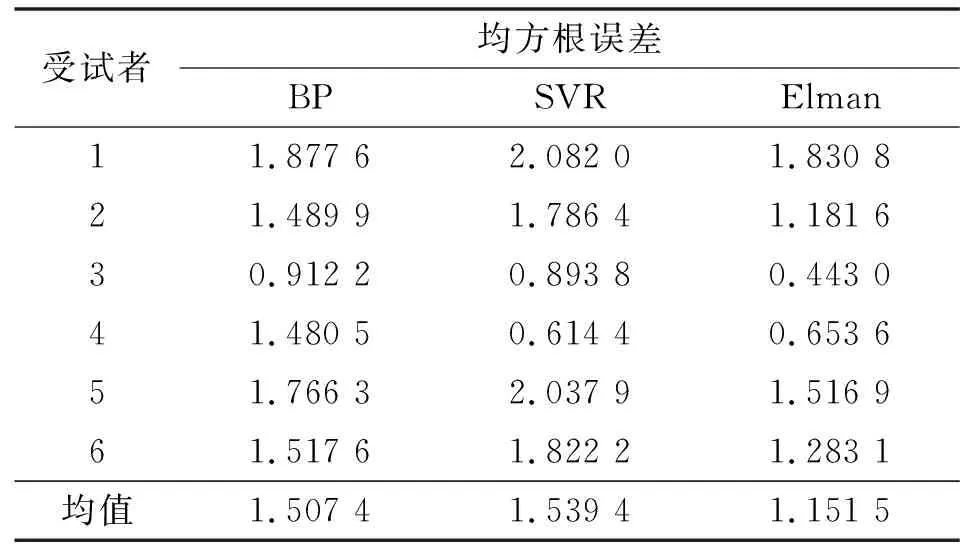
表1 BP、SVR、Elman均方根误差统计Tab.1 BP,SVR,Elman mean square root error statistics
2.3 基于麻雀搜索算法优化的Elman神经网络预测方法
此研究采用麻雀搜索算法(Sparrow Search Algorithm,SSA)优化Elman网络。SSA是一种新的群体智能优化算法,其设计灵感来源于自然界麻雀种群的群体觅食行为。麻雀种群中的个体通过不断调整分布位置来适应环境,从而获得更好的食物资源,避免捕食者的攻击。麻雀搜索算法已被证明优于许多传统的种群智能优化算法,因为它能够找到最好的并避免陷入局部极端。SSA的数学模型如下:
在模拟种群中,假设虚拟麻雀正在觅食,则由n只麻雀组成的麻雀种群可以用矩阵(9)表示:
(9)
其中:n表示种群中所有麻雀的数量;d描述决策变量的维度。
所有麻雀的适应度值可由式(10)表示:
(10)
麻雀搜索算法分为3个阶段:发现者、加入者和警戒者。顾名思义,发现者发现食物、寻找食物并为鸟群中的其他个体提供方向。因此,发现者寻找食物种类繁多,占鸟群总数的20%。发现者的位置更新公式为
(11)
式中:h表示当代迭代次数;M为最大迭代次数;xi,j表示第i个麻雀在第j维的当前位置;α∈(0,1)为随机数;R2(R2∈[0,1])和T(T∈[0.5,1])分别表示警告值和安全值;Q是服从正态分布的随机数;L表示一个1×d的矩阵,其中该矩阵内每个元素全部为1。
追随者在发现者和发现者位置周围的社区搜索之后执行食物搜索。追随者的位置更新公式如下:
(12)
式中:xp是发现者当前占据的最优位置;xworst表示当前最差位置;A是1×d且每个元素的取值为1或-1的矩阵,并且A+=AT(AAT)-1。
警戒者是在人群中随机选择的个体。当掠食者入侵时,它们会发出信号让麻雀逃到安全的位置。警戒者的行为公式如下:
(13)
式中:fi≠fg表明麻雀处于边缘位置,容易受到捕食者的攻击;fi=fg表明种群中的麻雀已经意识到了危险,需要靠近其他麻雀,以免被捕食者抓住。
麻雀搜索算法优化Elman神经网络的流程如图9所示。
适应度函数f设计为测试集的绝对误差和:
(14)
2.4 预测结果分析
一位受试者在不同运动模式下的多关节连续运动预测交叉验证结果如图10—12所示。
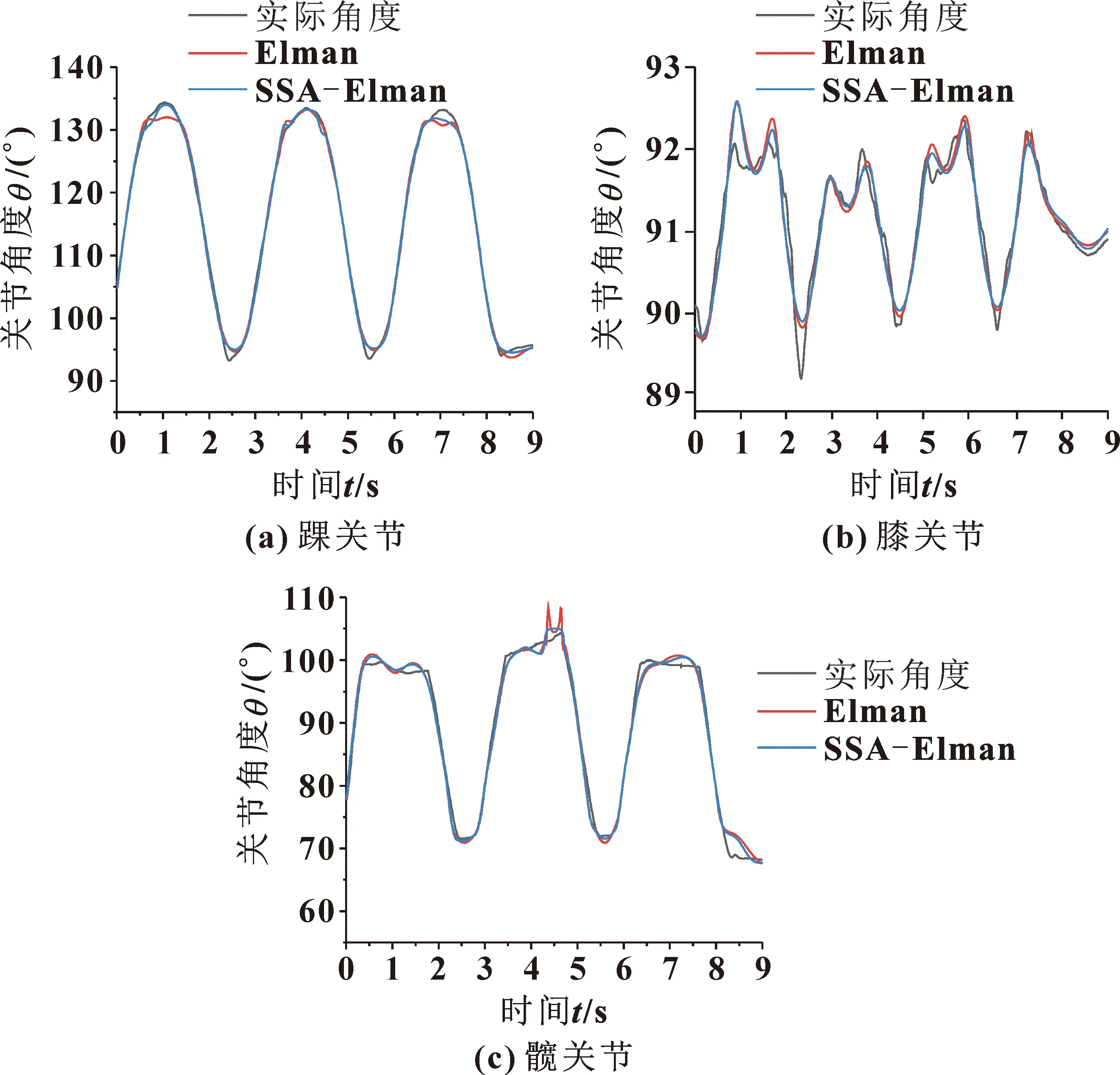
图10 蹲起运动关节角度预测结果Fig.10 Prediction values of joint angles in squat motion:(a) ankle joint;(b)knee joint;(c)hip joint
蹲起运动的下肢踝、膝、髋关节预测曲线如图10所示。可以看出:预测曲线与实际曲线十分接近,准确反映了关节运动的趋势。
膝屈伸运动的下肢踝、膝、髋关节预测曲线如图11所示。可以看出:踝关节运动曲线存在一定的抖动情况,说明人体在做下肢屈伸运动时,不能较好控制下肢踝关节保持一个稳定的状态,导致运动曲线出现了抖动的情况。虽然,踝关节的预测曲线与实际曲线局部有一定的偏差,但是整体预测效果表现较好。
上下阶梯运动的下肢踝、膝、髋关节运动曲线如图12所示。可以看出:下肢各关节均出现了波动情况,说明人在上下阶梯运动时,各关节并不是固定不动的,会有一定程度的活动范围。从膝关节的预测结果中可以看出Elman神经网络预测曲线出现了局部抖动的情况,这可能是由于肌电信号滤波效果不理想导致的。为了消除这种抖动现象,应该探索一种优化肌电信号滤波方法。从图12还可以看出:关节运动出现了较陡的拐点,预测结果不是很理想。这是由于较陡的拐点被认作为高频信号被滤波器过滤掉,导致了峰值数据失真,影响了预测精度。
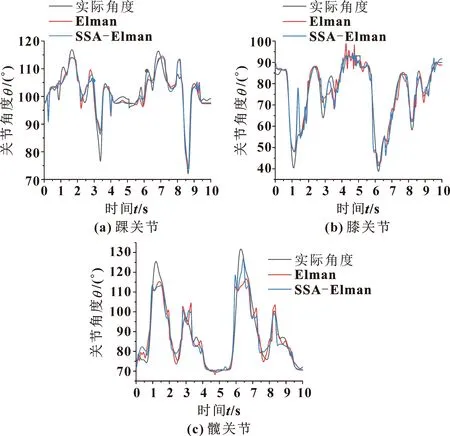
图12 上下阶梯运动关节预测结果Fig.12 Prediction values of joints with up-and-down step motion:(a)ankle joint;(b)knee joint; (c)hip joint
经过6名受试者的实验数据可以得出Elman和SSA优化后的Elman神经网络预测的平均均方根误差如图13所示。蹲起运动中下肢踝、髋、膝关节平均均方根误差分别降低了6.58%、12.93%、3.07%;膝屈伸运动中下肢踝、膝、髋关节平均均方根误差分别降低了53%、19.75%、4.47%;上下阶梯运动中下肢踝、膝、髋关节平均均方根误差分别降低了24.9%、20.61%、15.78%。
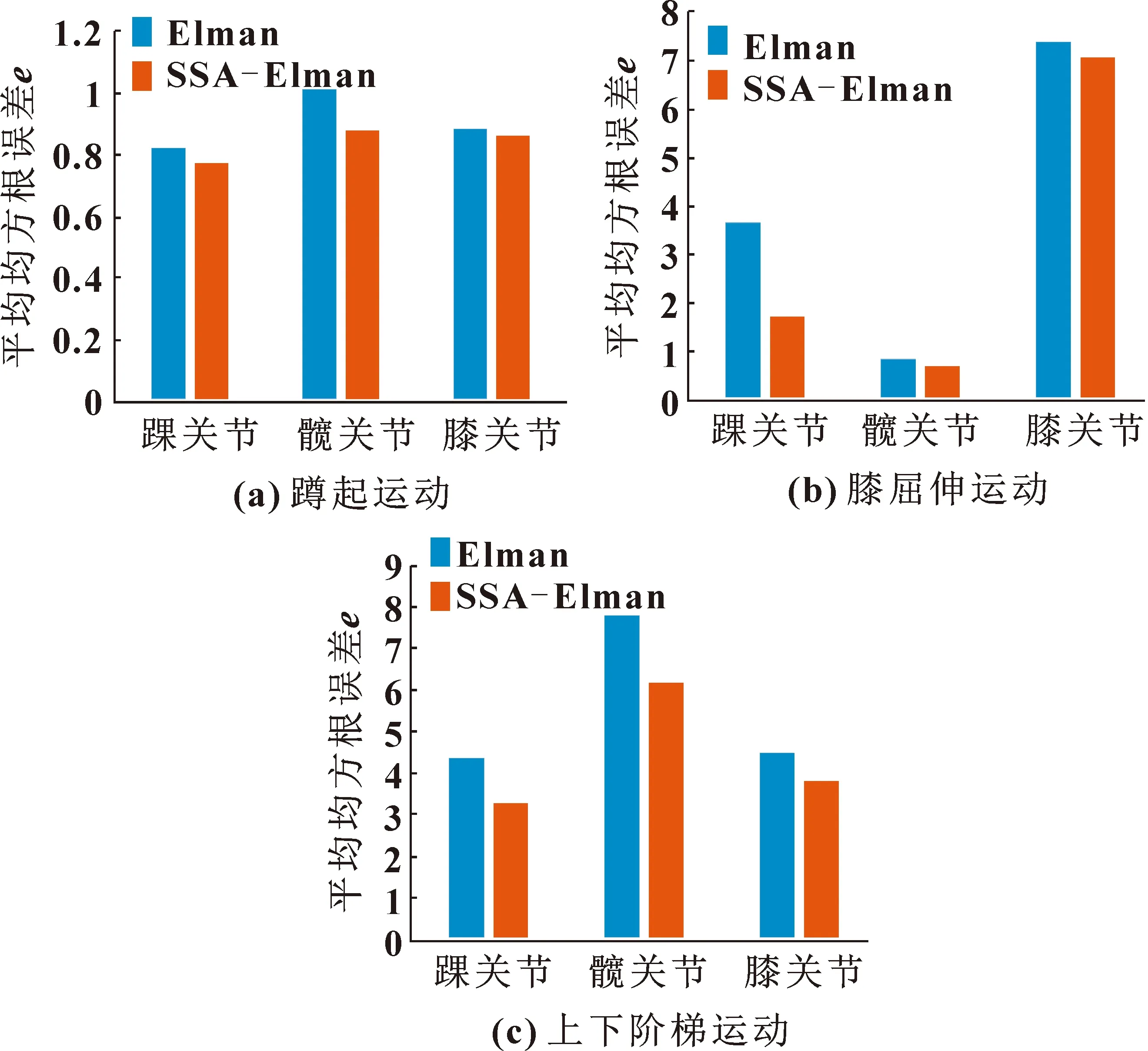
图13 Elman和SSA-Elman模型预测结果对比Fig.13 Comparison of prediction results between Elman and SSA-Elman model:(a)squatting motion;(b) knee flexion and extension motion;(c) up-and-down step motion
由表2统计分析可知:在蹲起运动中各关节预测的平均均方根误差最小,上下阶梯运动中各关节预测的平均均方根误差较大。这是由于上下阶梯运动出现了多处较陡的拐点,此处的高频信号被滤波器过滤掉,导致峰值数据失真,影响了预测精度。在预测结果中,各关节的平均相关系数均大于0.89,其中,蹲起运动中各关节相关系数更加接近1,表现出较强的相关性。这是由于蹲起运动具有一定的周期性且不会出现高频抖动,有利于预测出更好的结果,表明肌电信号可以较好地反映关节运动变化。

表2 受试者在不同运动模式下平均均方根和相关系数统计Tab.2 Statistics of root mean square and correlation coefficient of subjects in different movement patterns
3 结论
本文作者提出一种利用肌电信号进行下肢多关节连续运动预测的方法,可以实时捕捉人体下肢关节在不同运动模式下的运动状态。在该实现中,利用麻雀搜索算法优化的Elman神经网络在预测下肢关节角度变化中具有更高的精度,且该模型仅利用两块下肢肌肉的肌电信号,获得较好的预测效果,有利于应用于实际。该模型有望开发人机交互界面,实现持续的生物电控制,提高人机之间的稳定性,可应用于下肢外骨骼康复机器人、下肢助力外骨骼机器人及智能假肢等康复设备,适应不同运动模式下的康复训练和辅助行走,提供更好的仿生模式和适应能力。由于本文作者研究的是正常人体的下肢运动,未来的工作,可采集下肢功能障碍的病人运动数据进行研究。
