含间隙非线性的工业机器人关节振动特性分析
2023-12-04仪凌霄潘斯宁刘志成刘应忠
仪凌霄,潘斯宁,2,刘志成,刘应忠
(1.贺州学院人工智能学院,广西贺州 542899;2.桂林电子科技大学机电工程学院,广西桂林 541004)
0 前言
随着我国从制造大国向制造强国的战略转型,工业机器人的技术水平在不断提升,但我国目前在高精度、高性能等技术领域仍旧较国外存在差距[1-2]。由于工业机器人关节长期作业使得关节出现磨损,进而导致关节出现间隙,加剧关节传动系统的谐振,直接影响工业机器人关节运动的稳定性和末端定位精度。
杨立欢等[3]为探究减速器间隙对机械臂动力学特性的影响,提高机械臂的控制及摆位精度,建立了RV减速器中心轮与行星轮之间的齿侧间隙动力学模型,通过仿真验证表明关节齿侧间隙会使加速度出现非周期波动且波动幅值随间隙增加而增大。郑坤明、张秋菊[4]为研究关节间隙对定位精度的影响,以Delta机器人为研究对象,通过对机器人关节间隙的运动学分析,并结合 Lankarani-Nikravesh的间隙广义碰撞力研究,验证了间隙模型的合理性与正确性。苏成志等[5]为解决机器人运行中关节处的异响和振动现象,建立关节运动副间隙模型,分析了系统的固有频率。张珩、肖歆昕[6]从伺服系统的振动角度考虑齿轮传动中的间隙,通过闭环弱自激振动策略推导出新的间隙辨识方法。根据现有研究结果可以看出:关节间隙的存在仅会降低机器人的各阶固有频率,不会影响系统的模态振型。以上学者从振动角度分析关节间隙,但并未考虑关节传动过程中机电耦合等因素对机械臂的影响。
杜志江等[7]为提高关节建模精度,用迟滞模型描述关节非线性间隙特性,通过对模型的仿真分析,能够精确描述关节特性并提高了关节建模精度。史晓鸣等[8]为揭示间隙对舵机的影响,基于希尔伯特变化针对舵机间隙设计出新的参数辨识方法,结果表明该辨识方法能准确识别出舵机的真实间隙参数。薛邵文等[9]为解决含间隙机器人关节参数难以精确获取等问题,利用改进遗传算法对二连杆机构进行参数辨识,研究结果表明改进遗传算法辨识精度较传统算法高,收敛速度快。但在实际辨识中,作者将工业机器人简化为二连杆,忽略了实际关节中存在的刚度阻尼等关键信息。瑞典 Chalmers 大学的 LAGERBERG[10]针对机电耦合系统中存在的非线性间隙设计了主、被动式间隙控制器,并对系统中存在的间隙提出了优化补偿算法。上述学者均是在间隙值已知或假设条件下开展的工作,并未从工业机器人实际工况中获取关节的间隙参数。
综上所述,国内外大部分学者的研究都是基于间隙本身的机制开展分析,更加侧重研究间隙环节中输入与输出间的非线性特征,但工业机器人实际作业时,更多表现在关节传动中的位移关系。本文作者以钱江QJR6-1型工业机器人为研究对象,采用关节系统的理论建模、仿真分析、单关节摆臂实验测试和参数辨识相结合的研究方法,对含间隙非线性关节展开振动特性研究。
1 关节间隙非线性动力学建模
为分析间隙非线性模型在实际应用控制领域的影响,本文作者以钱江QJR6-1型工业机器人为研究对象,如图1所示。该实验平台由六自由度串联机器人本体、示教器、控制箱以及PC工控机等组成。机器人关节是由伺服同步电机与减速器以及联轴器组成的系统。

图1 QJR6-1型工业机器人Fig.1 QJR6-1 industrial robot
1.1 建立关节间隙简化模型
为了深入研究工业机器人关节的运动规律以及间隙对关节性能的影响,需将图1中的关节系统进行简化[11-12],如图2所示,并建立含间隙非线性关节动力学模型。
图中:Je、Jm、JL分别为关节的伺服驱动电机、减速器和关节臂的转动惯量;C1、C2、C3、Cw1、Cw2分别为伺服电机、减速器、关节臂、联轴器1和联轴器2的黏滞阻尼系数;Te、Tm、Tw1、Tw2分别为伺服电机的电磁转矩、关节臂转矩、联轴器1和联轴器2的转动扭矩;Kw1、Kw2分别为联轴器轴1和联轴器2的刚度系数;B为关节间隙系数。
根据旋转系统的动力学原理推导出含间隙关节系统的动力学方程为
(1)
式中:θ1、θ2、θ3分别为关节伺服驱动电机、减速器和关节臂的旋转角度;i为关节减速比。
1.2 关节间隙数学建模
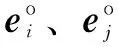
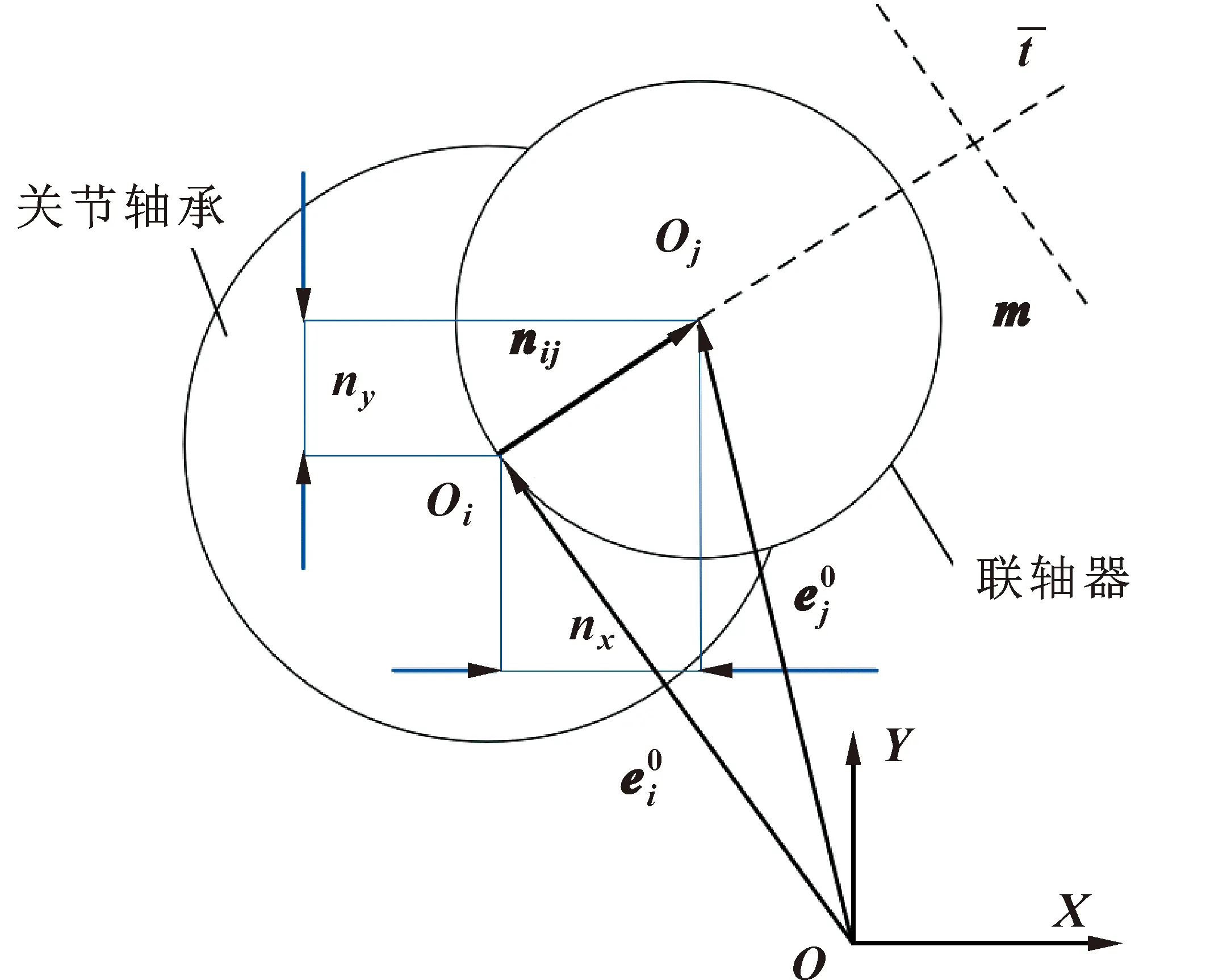
图3 关节间隙数学模型Fig.3 Mathematical model of joint clearance
图3中:nx代表关节间隙矢量nij在X轴方向的数值分量,ny代表关节间隙矢量nij在Y轴方向的数值分量,其关系表达式为
(2)
其中关节间隙nij又被称为偏心距,是表示关节轴承与联轴器轴径的中心距。关节间隙法向矢量大小表达式为
t=nij/nij
(3)
式中:t为关节间隙的法向矢量,将其旋转90°得到关节间隙切向矢量m。
通过引入关节间隙的矢量范围以及间隙大小,可推导出关节运动副间的接触形变。其中间隙系数的大小B等于关节轴承半径与联轴器轴径半径之差,令δ为接触形变量,其关系表达式为
δ=nij-B
(4)
通过对接触形变量δ的分析,可以得到关节运动副之间的相对运动状态。当接触形变量δ≥0时,关节运动副处于相对碰撞阶段,在该状态下会产生碰撞形变;当接触形变量δ<0时,关节的轴承与联轴器处于相对分离的状态,其表达式为
(5)
当工业机器人末端处于非接触工况条件时,不受外力冲击的关节系统属于线性运动范畴;当触及工况条件时系统因形变而演化为非线性运动,进而使关节运动轨迹处于混沌状态。
2 关节间隙非线性振动分析
由于关节间隙的存在,工业机器人在启动、制动以及变负载作业时会产生冲击现象,降低了关节系统的可靠性,较大的间隙值会使关节系统的响应超调,进而降低工业机器人末端定位精度。为解决因非线性间隙而导致关节系统处于非平稳状态,揭示含间隙关节振动机制,对关节非线性间隙进行振动特性分析。
2.1 建立仿真模型
QJR6-1型机器人由多个旋转关节串联而成,当某个关节因非线性因素使系统产生异常振动,将严重破坏轴系部件以及影响工业机器人设备寿命。根据含间隙关节系统的动力学方程建立其仿真模型,如图4所示(不包括红色双点划线线框部分)。关节系统的主要参数见表1。

表1 关节系统主要参数Tab.1 Main parameters of the joint system
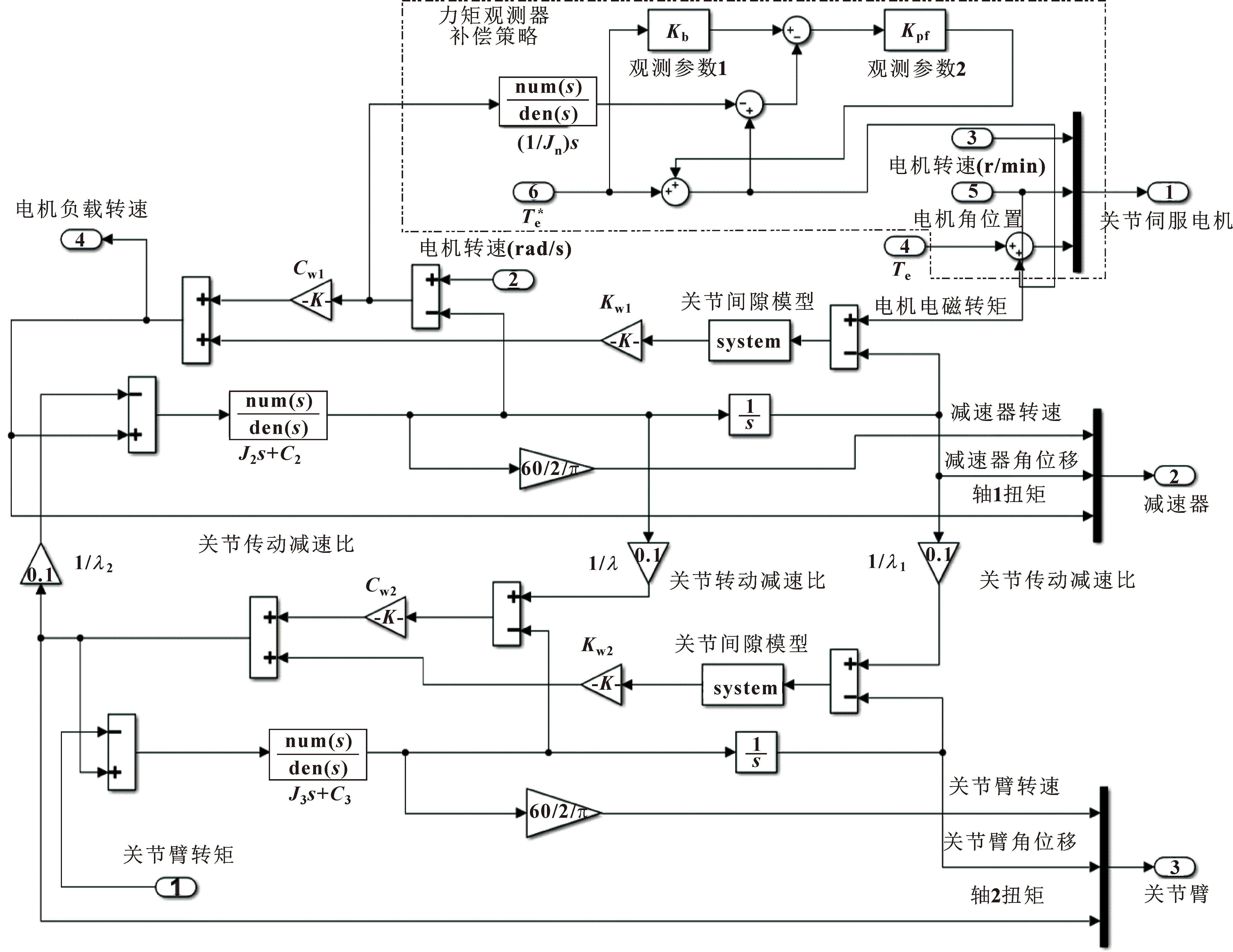
图4 含间隙的关节传动模型Fig.4 Joint transmission model with clearance
图4中:J1、J2、J3分别为关节的伺服驱动电机、减速器和关节臂的转动惯量;λ为关节减速比。
2.2 关节间隙稳定性分析
关节间隙的存在会降低关节传动系统的稳定性及抗干扰能力,影响工业机器人的正常运行,而关节联轴器的刚度值不是无穷大,间隙的出现则会加剧关节系统的谐振。
由式(1)可推导出关节电机的转速到关节电磁转矩的传递函数:
(6)
由式(6)看出关节系统由惯性环节及二阶振荡环节构成,当关节系统处于低频时,由于是单惯量则不存在扭振,而当关节系统处于中高频时,二阶振荡环节中的柔性和间隙值则会产生扭振。
令式(6)分子和分母为0,分别得到关节系统的谐振频率fN及抗谐振频率fA:
(7)
(8)
由上式可推导出含间隙关节系统的频域特性中的谐振频率及抗谐振频率,如图5所示。

图5 含间隙频率特性曲线Fig.5 Frequency characteristic curve with clearance
由图5可以看出关节的谐振频率为123.16 Hz,幅值大小为25.29 dB,关节的抗谐振频率为44.63 Hz,幅值大小为-14.02 dB。而关节的抗谐振频率点对整个系统的抑制作用较小,可以看出由于间隙的影响,关节系统易受外界相近频率的干扰引起关节轴系的振荡,破坏其稳定性。
2.3 含间隙关节振动特性仿真
根据建立的关节系统模型,并结合工业机器人实际关节工况所产生的间隙进行换算[18],设置关节间隙值xbacklash=0.000 1 m和xbacklash=0.001 m,并对关节臂、关节伺服电机、联轴器等关键部件进行振动特性仿真分析。
如图6所示,由于间隙非线性的存在使得关节臂的转速受到影响,随着间隙值不断增加,关节臂的转速波动也愈加明显,且速度波动频率也随间隙值的增加而变快,可以看出关节臂转速在趋于稳定工况时,速度波动的幅度达到了±2 r/min,这也将导致工业机器人末端定位精度的稳定性变差。
如图7所示,关节伺服电机的电磁转矩振幅随间隙值的增大而增大。对比图7(a)与图7(b)可看出:当存在较小间隙时整体电磁转矩振幅无明显变化,但稳定时的关节电磁转矩出现了明显的波动。从图7(c)可以看出:当间隙增大之后,关节的电磁转矩振幅波动范围从6~10 N·m变化到1~16 N·m。

图7 含间隙电磁转矩时域振动信号Fig.7 Time domain vibration signals of electromagnetic torque with clearance:(a)without clearance; (b)xbacklash=0.000 1 m;(c)xbacklash=0.001 m
如图8所示,关节的联轴器相较于电机由于刚度的存在而出现了滞后现象。对比图8(a)与图8(b)可以看出:趋于稳定时的关节联轴器振动幅值因间隙的存在出现了较大的波动,其波动范围在-5~5 N·m。从图8(c)可以看出增大间隙值关节联轴器振动范围变化到-60~60 N·m。
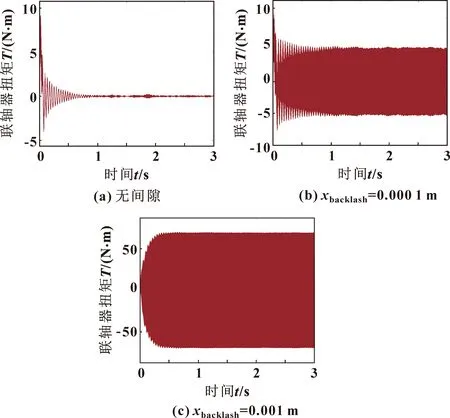
图8 含间隙联轴器时域振动信号Fig.8 Time domain vibration signals including clearance coupling:(a)without clearance;(b)xbacklash= 0.000 1 m;(c)xbacklash=0.001 m
如图9所示,为了更加直观地分析间隙非线性对关节联轴器的振动影响,对图8的时域振动信号进行频谱分析。从图9(a)可以看出:当间隙值为0.000 1 m时,关节联轴器的最大振动幅值出现在频率77 Hz处,振幅仅为2.9 dB;当间隙值为0.001 m时,关节联轴器的最大振动幅值出现在频率102 Hz处,但振动幅值随间隙的增大变化至54 dB;而当关节无间隙时振动幅值却只有0.05 dB,如图9(b)所示。

图9 关节联轴器频谱分析Fig.9 Spectrum analyses of joint coupling:(a)clearance is 0.000 1 m or 0.001 m;(b)without clearance
从以上的分析可以看出,间隙对频率的影响不明显但对振动幅值有较大影响,因此可以推导出间隙不仅会降低系统的动态特性,破坏关节系统的稳定性,还会加剧关节零部件的损害。
3 实验验证与间隙补偿
3.1 间隙实验测试
为进一步通过实验验证模型的准确性,根据关节简化模型搭建单关节摆臂实验台,如图10所示。该关节传动实验台由伺服驱动器、伺服同步电机、减速器、编码器、电流传感器以及关节臂等部件组成,其设备型号如表2所示。通过改变联轴器与关节臂的相对位置,模拟工业机器人在含间隙时的运动状态,并采集其电流信号和振动信号。
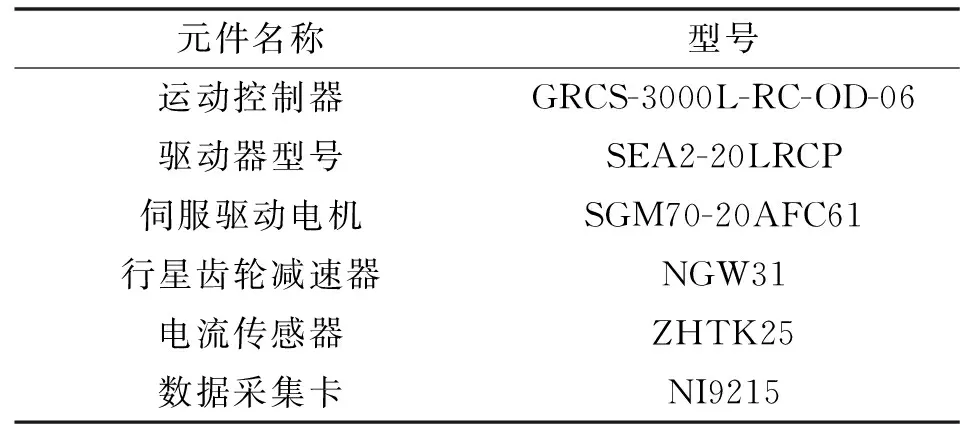
表2 实验设备型号Tab.2 Models of experimental equipments

图10 关节传动模拟实验台Fig.10 Joint drive simulation test bench
此次单关节摆臂测试对象为伺服同步电机的电流信号,为更加准确地模拟实际工况状态,测试时将设置减速器及联轴器间隙值,并在关节臂上添加15 A负载电流。设置伺服同步电机的测试转速为1 000 r/min,其中摆臂台减速器的减速比为1∶10。使用电流互感器实时采集伺服同步电机的三相电流信号,设置摆臂试验台信号采集频率为25 600 Hz,并连接数据采集卡对其电流信号进行高分辨率测量,最后将信号传递至工控机,对实验数据进行存储、处理、分析等。
图11所示为含间隙单关节摆臂实验电流信号的时域波形图,可以看出信号发生周期性波动。引起该电流信号变化的原因是关节的摆臂运动,而周期性则说明了该关节模拟实际工况中的往复运动。
图12所示为实验数据和仿真辨识数据所产生的频响振幅谱,可看出:只考虑共振频率与抗共振频率的位置时,辨识共振频率与实验共振频率吻合度较好,但由于拟合时忽略了阻尼效应以及实验中的噪声干扰,导致实验与仿真振幅之间存在一定的差异。
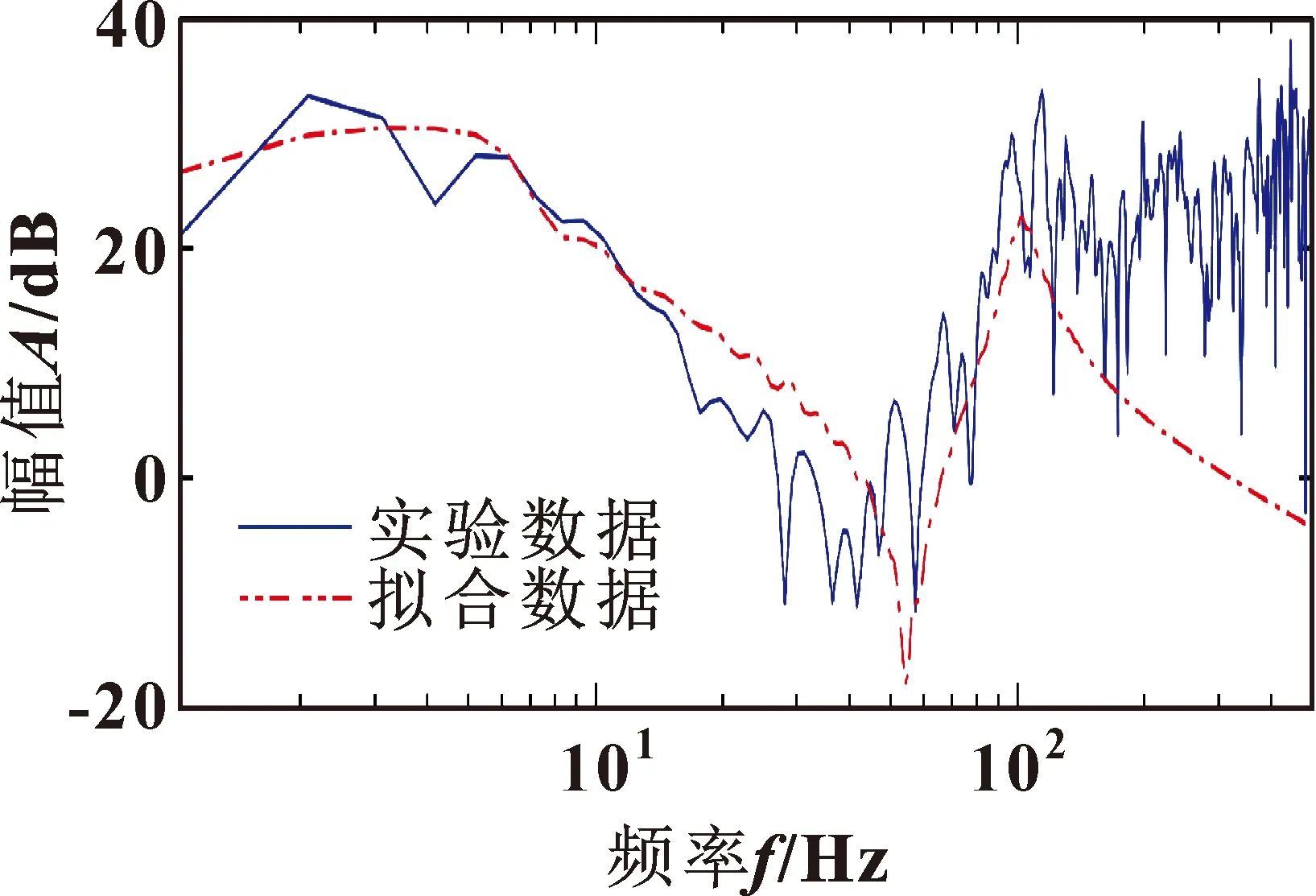
图12 摆臂实验台频率响应Fig.12 Frequency response of swing arm test bench
3.2 关节非线性间隙补偿
为解决由关节间隙而产生的谐振问题,主要从两个方面入手[19-20]:一种是通过紧固传动构件降低系统的弹性,此方法操作复杂且无法彻底消除弹性因素;另一种是对给定速度值的调节,降低速度或其变化率从而避免与关节频率重叠,但会影响关节动态性能。本文作者从力矩补偿的角度,对关节非线性间隙进行补偿。
在图4所示的关节间隙模型中,如果关节臂转矩TL=0且无间隙,则补偿电磁转矩Te值可由公式(9)—(12)推导:
(9)
(10)
(11)
Tw=Jm/(Je+Jm)Te=KbTe
(12)
当电磁转矩有一个力矩观测估计,且含间隙关节系统以等式(12)的方式设置其转矩值,能够消除关节臂的扰动从而达到间隙补偿的效果。如图4所示,将力矩观测补偿策略(双点划线框中所示)应用在含间隙的关节系统中。在该转矩观测补偿策略中,观测器中Kpf、Kb的值分别为轴矩传递系数以及力矩传递系数,而Jn为关节驱动伺服电机惯量的估计值。
为验证力矩补偿策略的有效性,以单关节摆臂实验台为测试对象,使用工控机中的软件进行程序设置,将PWM参数指令通过串口发送至伺服驱动器并驱动电机运行,最终采集实验所需的电流信号如图13所示。由实验结果对比可知:关节非线性间隙补偿对电流一些波峰处有不同程度的减小,但数据采集时受工况环境的干扰,整体电流波动情况呈现小幅度局部改善。
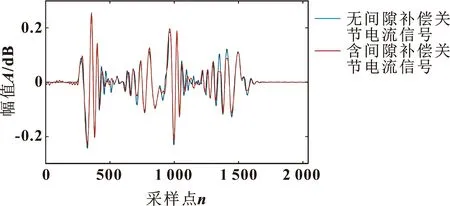
图13 补偿前后的电流时域信号Fig.13 Current time domain signals before and after compensation
4 结论
本文作者以钱江QJR6-1型工业机器人为研究对象,针对关节存在的间隙非线性进行振动特性分析。
(1)将含关节系统简化为“伺服同步电机+减速器+联轴器+关节臂”的机电耦合传动系统,并建立含间隙非线性关节动力学模型。
(2)分析含间隙关节系统谐振频率,并对关节系统中重要零部件在不同间隙值时的扭转振动特性进行了仿真分析。随着间隙值的增大,将减弱关节系统的稳定性。
(3)为验证振动特性研究的准确性,搭建了单关节摆臂测试台,对关节电流信号进行采集并对振动信号频域响应进行对比,实验和仿真结果表明了该振动分析方法的有效性。
(4)对关节的间隙非线性进行了力矩补偿,补偿后电流信号在一些波峰处有不同程度的减小。
