基于二次强度调制的激光测距系统*

王菊 邵琦 于晋龙 何可瑞 罗浩 马闯 蔡滋恒 郑紫月 蔡奔

(天津大学电气自动化与信息工程学院,天津 300072)

本文提出的二次强度调制测距系统可以实现绝对距离的测量,其利用马赫曾德尔强度调制器代替二次偏振调制测距中的电光相位调制器,通过对信号的光强进行二次调制来进行测距.相比于二次偏振调制测距,二次强度调制测距无需考虑测距系统中的偏振态问题,简化了系统结构,提高了系统的稳定性.经过相关理论推导以及实验验证: 二次强度调制测距系统的输出光强与调制频率成余弦关系,并且可以直接测量调制器到目标物体之间的绝对距离,系统的频率稳定度、相对测距精度皆达到10–7 量级.本文提出的测距系统量程达到100 m,相对测距精度稳定在10–7 量级.采用摇摆法快速测距,避免了直接扫频寻找光强极小值点对应的频率,数据刷新率达到2 kHz.二次强度调制测距系统测距速度快,同时兼顾了较大的量程与较好的测距精度,系统结构简单,易于搭建,具有广阔的应用前景.

1 引言

近年来,高精度、大量程的快速测距在大型设备制造、精密仪器装配、航空航天、军事国防等科学工程领域的应用愈加广泛.在我国的火星探测工程中,祝融号火星车成功软着陆火星地表后,需要其相对定位精度在距离10 m 左右时优于3%[1];在大型客机的生产制造过程中,各个部位工件加工精度与定位精度都需要达到毫米量级[2];在载人空间站的交会对接中,目标相对测距机高速移动,不仅需要高精度的绝对距离测量(毫米量级),还需要足够的测距速率(3 Hz)以保证实时有效的跟踪控制[3].

目前,绝对距离激光测距技术分为相干测量和非相干测量两大类.相干测量以基于飞秒光频率梳的干涉测距为研究热点[4–10],它在大量程的高精度测量中具有很大的应用潜力,但由于飞秒光频率梳的高昂成本,尚不能广泛应用于工业测量.此外,激光干涉也被应用在引力波探测中,并取得了巨大的成功.当引力波经过干涉仪的测量臂时,通过干涉激光相位变化推导出测试质量间的距离变化,从而反演得到引力波信息.欧洲航天局(ESA)和美国航空航天局(NASA)合作的引力波探测计划LISA,通过利用空间卫星构建空间激光干涉仪,可以测量百万公里量级的皮米级距离变化[11].国内的太极计划和天琴计划也将激光干涉技术应用于引力波探测,并分别于2019 年8 月和2019 年12 月发射了实验验证卫星.经过实验测试,他们构建的空间激光干涉仪也都可以实现皮米量级的超高精度距离测量[12,13].非相干测量中常用的技术手段包括脉冲测距法[14–16]、微波相位测距法[17–19].脉冲测距法通过测量激光往返待测路径的飞行时间来测得往返距离,现阶段该方法主要用于超长距离测距,测距精度一般在毫米甚至厘米量级[16].微波相位法测距是对测量光进行正弦调制,通过比较激光往返待测距离的相位变化获取距离信息.微波相位法测距是一种比较成熟的测距方案,在几十厘米至几百米的测距范围内测距精度可以达到毫米甚至亚毫米量级[17,18],并且可以实现0.03 s/次[19]的测距速度.但要想进一步提升测距性能,还需要进一步优化系统的鉴相模块.

二次偏振调制测距结合了相位法和干涉法的测距优点,利用相位调制器对光信号进行两次偏振调制,再经由干涉解调,最终通过输出信号的相邻光强极值点对应的调制频率变化获取距离信息.黑克非[20]、肖洋[21]、高书苑等[22,23]都曾先后进行过相关研究,并取得了一定的研究成果;2022 年,高超等[24]尝试的波导式相位调制器测距系统,利用光纤延时线测量得到的测距误差为0.39 mm.二次偏振调制测距方法由传统的对时间、相位的测量转变为对光强的测量,同时兼顾了较大的量程与较好的测距精度,在工业领域中有很大的应用潜力.但为了实现光的偏振调制,需要用到偏振分光棱镜(PBS)进行起偏,测量过程中偏振态的扰动也会在调制时引入额外的噪声,影响测试精度.此外,测距过程中还需要在目标物体之前放置1/4 波片或者法拉第旋光镜进行偏振态的调整,这使得系统的复杂度增加,限制了应用场景.

二次强度调制测距系统利用马赫曾德尔强度调制器代替二次偏振调制测距系统中的相位调制器,与二次偏振调制测距一样,二次强度调制测距也是通过解调后的光强反演得出距离信息,理论上可以达到和二次偏振调制相同的测距效果.而相比二次偏振调制测距,二次强度调制测距通过对光的强度调制代替偏振调制,激光器输出的光信号不用PBS 进行起偏,可以直接输入到强度调制器中进行调制,两次调制间的光信号也无需进行偏振态的调整.整个系统的结构可得到充分简化,能适应更多不同的测量场景,更有利于后续的工业化设计.

本文对二次强度调制测距原理进行了理论分析,推导证明了系统输出光强度和调制频率满足余弦函数关系,并进行了实验验证.实验结果表明:二次强度调制测距系统可以实现调制器到目标物体之间的绝对距离测量,系统的频率稳定度以及相对测距精度都在10–7量级,测距量程达到100 m.此外,本文提出通过摇摆法间接找寻光强极小值点对应的频率,不仅提高了测距数据刷新率(2 kHz),还降低了噪声的影响.

2 二次强度调制测距系统

2.1 测距原理

图1 是本文提出的二次强度调制测距原理图,激光器输出信号由环形器1 端口输入,2 端口输出进入马赫-曾德尔强度调制器,假设激光的光场强度为E0,频率为ω0,初始相位为ϕ0,则进入调制器的光信号可表示为

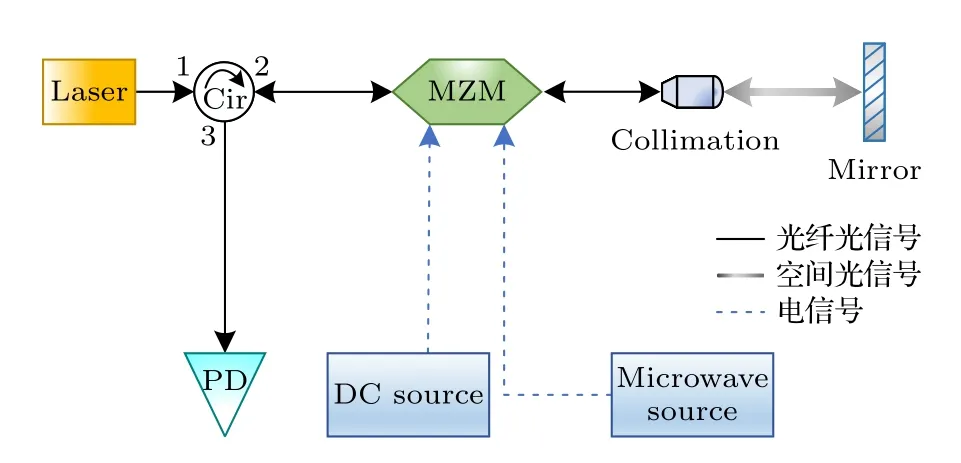
图1 二次强度调制原理示意图(Cir,环形器;MZM,马赫曾德尔调制器;PD,光电探测器)Fig.1.Schematic diagram of double intensity modulation(Cir,circulator; MZM,Mach-Zehnder modulator; PD,photo detector).

图2 马赫-曾德尔调制器传输曲线Fig.2.Transmission curve of Mach-Zehnder modulator.

马赫-曾德尔强度调制器的调制原理是将输入光分为振幅、相位相等的两束光.通过对其中一束光施加外部电场进行相位调制,使上下两束光信号产生相位差.两束光在输出端干涉叠加时的光强会随着两束光信号的相位差改变,从而实现外部电场对光信号的强度调制[25].定义调制器的半波电压参数为Vπ,表示两路信号相位差为 π 时引入的外电场.则当外部电场的直流电压为Vdc,射频部分为Vaccos(ωact)时,经过马赫-曾德尔调制器后的输出光信号可表示为[26]

式中,φbias=πVdc/Vπ表示调制器的外部直流偏置,m=πVac/Vπ表示调制器的调制深度.

调制器第一次调制后的光信号经过一段待测距离后到达反射镜反射,光信号沿原路返回,返回的光信号再次经过调制器进行第2 次调制:

第2 次调制时,由于光信号从调制器的输出端进入,调制器的调制深度与第1 次有所不同[27]:其中τ为马赫-曾德尔强度调制器中信号的渡越时间.

可得信号光强为

马赫-曾德尔强度调制器根据不同的直流偏置,会在不同状态工作,图 2 为调制器在不同直流偏置下的传输曲线,其中有3 种典型的工作状态: 最大输出点、最小输出点和正交传输点.在本实验中,调节直流偏置电压Vdc=3Vπ/2,使其工作在斜率为正的正交传输点,此时理论上调制器的输出光信号功率P1的变化频率等于调制的射频信号Uac的频率,推导如下:

图3为J2n-1(m) 表示的第一类贝塞尔函数,实验中选取的强度调制器的半波电压Vπ为6 V,射频信号幅度Vac为600 mV,调制深度m约为0.31,此时贝塞尔函数一阶项系数为0.15,三阶项系数为0.0006.贝塞尔函数三阶及以上的高阶项远小于一阶项,因此可以忽略:

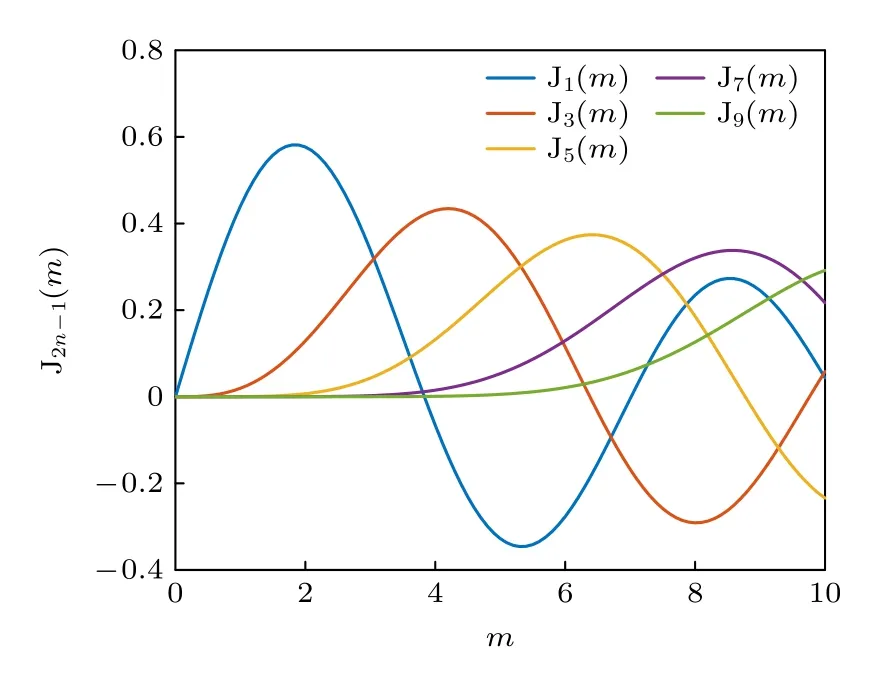
图3 第一类贝塞尔函数Fig.3.Bessel function of the first kind.

图4 二次强度调制测距实验结构图(Cir,环形器;MZM,马赫-曾德尔调制器;VOA,可调光衰减;PD,光电探测器;A/D,模数转换)Fig.4.Experimental structure diagram of double intensity modulation ranging (Cir,circulator;MZM,Mach-Zehnder modulator;VOA,variable optical attenuator;PD,photo detector;A/D,analog to digital converter).

图5 实验扫频曲线Fig.5.Experimental sweep curve.

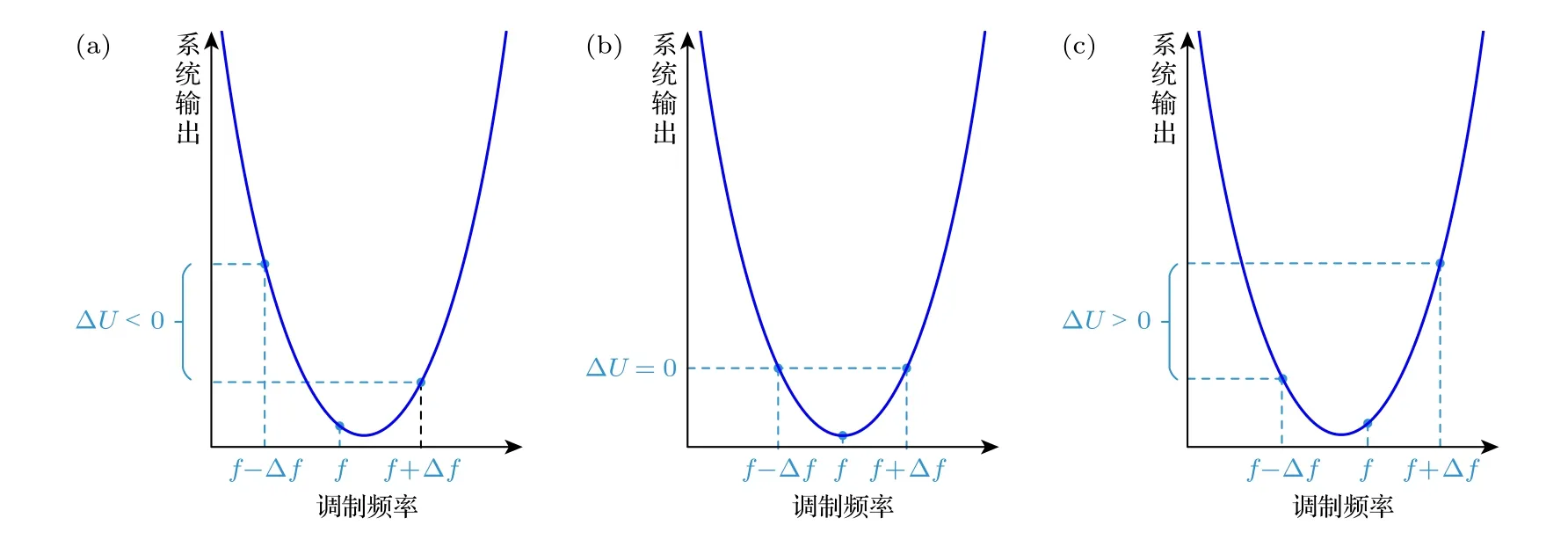
图6 不同位置下f与ΔU 的关系 (a) f 在光强极小值点对应频率的左侧;(b) f 为光强极小值点对应的频率;(c) f 在光强极小值点对应频率的右侧Fig.6.Relationship between f and ΔU at different positions: (a) f is on the left side of the frequency corresponding to the light intensity minimum point;(b) f is the frequency corresponding to the minimum point of light intensity;(c) f is on the right side of the frequency corresponding to the light intensity minimum point.

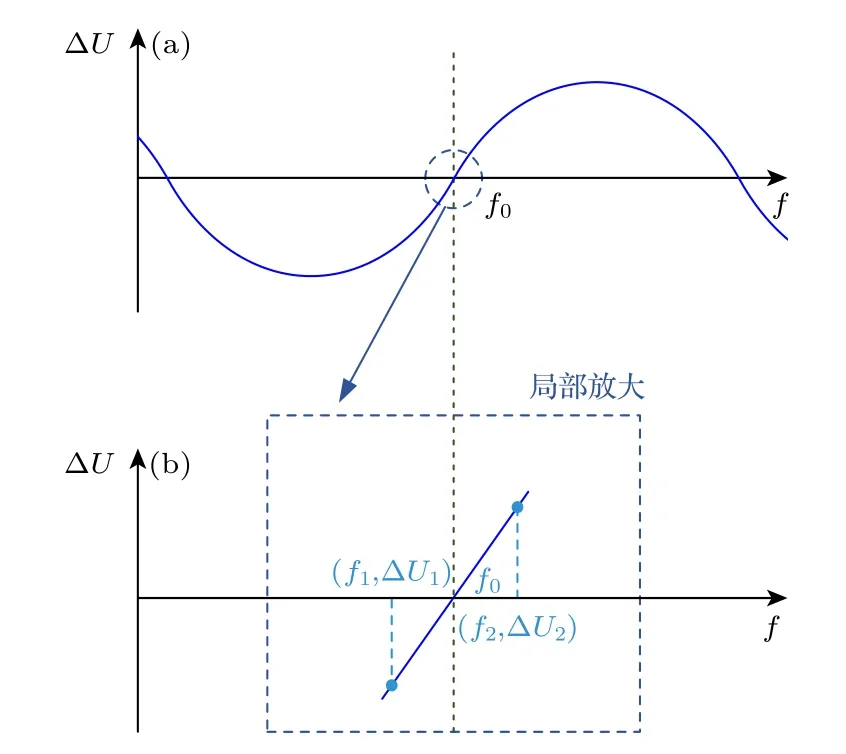
图7 摇摆差值曲线及其零点局部放大 (a)摇摆差值曲线;(b)摇摆差值零点局部放大Fig.7.Swing difference curve and local amplification at zero point: (a) Swing difference curve;(b) partial amplification of zero point of swing difference.

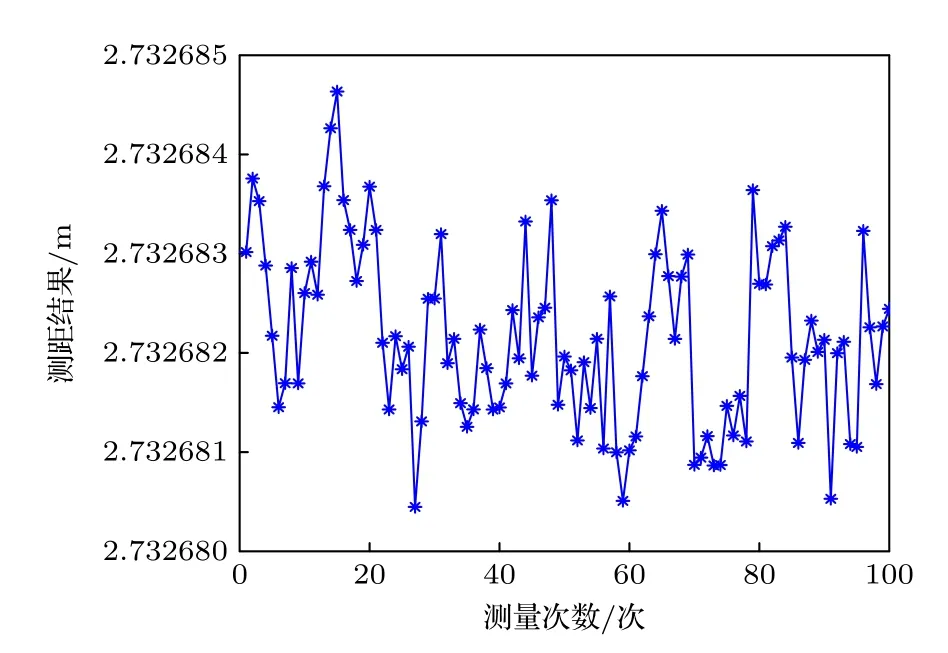
图8 系统测距结果Fig.8.Distance measurement results of the system.

同样,可以得到:

两次调制后的光信号再次经过环形器,由2 端口输入,3 端口输出进入光电探测器(PD)进行光电转换.当待测距离固定时,探测光的往返时间Δt是固定不变的,包含 cos(ωacΔt) 的部分为直流分量,而包含 cos(ωact) ,cos(2ωact) 的部分为交流分量.由于PD 的响应带宽远小于调制信号的频率,因此信号中除了直流分量以外,其他交流分量都被滤除,最终探测的信号光强Pout为

(1)加强对品管圈护理人员与患者的教育与知识宣传,向患者讲解内瘘穿刺的原理方法以及在穿刺时对患者的要求,并鼓励家属共同参与,提高护理人员及患者对内瘘穿刺点渗血的认识,以达到减少并尽量避免动静脉内瘘穿刺点渗血的效果。

2.2 连续扫频测距

(11)式表示PD 探测光强与调制信号角频率ωac以及信号飞行时间 Δt的乘积满足余弦函数关系.Δt可用待测距离D、真空中光速c以及空气的等效折射率n表示为

(13)式表明,当待测距离D确定,在 J1(m) 和J1(m′) 不变的前提下,PD 探测到的光功率随着fac的变化呈余弦变化.通过连续扫频的方法,找到相邻的两个光强极小值点对应的频率f1,f2,分别对应余弦曲线的 (2N-1)π ,(2N+1)π,则有:

联立两个方程可以得到待测距离D的表达式:

式中[·]表示取整运算.通过连续扫频测距方法,只需找到相邻两个光强极小值点对应的频率f1和f2即可求出最终的待测距离,无需考虑传统相位法测距中模糊距离的限制.

3 实验系统搭建

3.1 测距系统可行性分析

系统搭建完成后,对系统的测距可行性进行实验验证,控制射频源以100 kHz 为步进,进行100—400 MHz 范围内的扫频,再由电脑对AD 转换的数字信号进行分析处理.根据AD 转换器测量得到的光强信息绘制扫频曲线如图 5 所示,PD 的输出电压与调制频率满足三角函数关系,这与(13)式的推导一致.

3.2 摇摆法快速测距

根据(16)式可知,二次强度调制测距的关键是找到两个相邻的光强极小值点对应的频率.如果利用直接测量的方法寻找,需要从某个频率点开始进行多次频率扫描,极大地延长了测距时间.为了尽可能地缩短测距时间,提高数据刷新率,本文提出利用摇摆法进行快速测距.

根据(13)式以及图 5 可知,探测光强和调制频率成余弦关系.测量时选取中心频率f和偏移频率 Δf,由于余弦函数的对称性,可以根据调制频率分别为f+Δf和f-Δf的系统输出来判断中心频率f的位置.具体用频率为f+Δf时的系统输出减去频率为f-Δf时的系统输出,这个差值记作摇摆差值 ΔU,则当中心频率f位于不同位置时 ΔU的变化情况如图 6 所示.ΔU的表达式为

根据上述摇摆差值的计算方法,当偏移频率Δf固定,摇摆差值 ΔU与中心频率f满足正弦函数关系.随着中心频率f从扫频曲线极小值点的左侧移动到右侧,摇摆差值 ΔU的值从小于0 变化到大于0,具体关系曲线如图 7(a)所示,扫频曲线的极小值点对应的调制频率f0就是摇摆差值曲线的零点对应的调制频率.图 7(a)的摇摆差值曲线是一个正弦曲线,在其零点附近局部放大,可以近似为一条直线(如图 7(b)所示),选取中心频率f1与f2分别位于摇摆差值曲线零点对应调制频率f0的左右两侧,相应的摇摆差值 ΔU1小于0,ΔU2大于0.通过f1,f2,ΔU1以及 ΔU2的大小,就可以 拟合得到摇摆差值曲线零点对应的调制频率f0的具体数值:

根据(19)式可知,找到摇摆差值曲线零点对应频率两侧的两个频率值,再测量其相应的摇摆差值,即可得到扫频曲线极小值点对应的调制频率.具体方法: 设置合适的扫频间隔,根据 ΔU的正负判断当前频率与摇摆差值曲线零点对应频率的相对位置,最终找到4 组频率,确保它们包括两个相邻的摇摆差值曲线零点对应频率.通过这4 组频率及其摇摆差值计算得到扫频曲线连续两个光强极小值点对应的频率,将这两个频率值代入(16)式即可求出待测距离.扫频间隔的设置有两点原则,一是要尽可能的大,以减少扫频次数;二是待测距离大致确定时,摇摆差值曲线的周期也就大致确定,要使扫频间隔小于摇摆差值曲线周期的一半,确保每次扫频时不会漏掉摇摆差值曲线的零点.

相比于通过直接测量的方式找寻光强极小值点对应的频率,摇摆法所需要的跳频次数明显减少,这无疑极大地减少了测距时间.在当前的实验条件下,通过摇摆法快速测距,最高可以实现2 kHz的数据刷新率.除了快速测距,摇摆法的另一个优势是把光强极小值点的系统输出测量转变为对光强极小值点附近的输出测量.而相比于系统在光强极小值点时的输出,附近点的输出响应更大,受噪声的影响相对更小.

4 分析及讨论

4.1 绝对距离测量分析

由上述分析可知,根据系统的扫频曲线,结合摇摆法,可以实现调制器到待测目标之间的绝对距离测量.为了验证绝对距离测量的测距精度及其影响因素,实验选取待测距离2.73 m,对这段距离重复测量100 次,得到的100 组数据整合为图 8 所示的折线.

根据图 8 的测距结果可知: 100 次重复测距的结果均稳定在2.73 m,且波动不超过5 μm.对这些数据进一步进行分析计算,得到距离结果的标准差为1 μm,系统的相对测距精度为 3.66×10-7.

根据(16)式,测距结果与相邻光强极小值点对应的频率值有关,因此频率的稳定与否决定了系统的测距能力.为了进一步探究频率稳定度与测距精度的关系,(16)式对频率求导得

将(16)式代入(20)式得:

可以发现,系统相对测距精度的大小等于第一个频率极值点f1的相对稳定度大小.为了进一步验证它们的关系,实验进行3 组重复距离测试,每组进行30 次扫频测距,根据扫频曲线算出两个相邻光强极小值点对应的频率值.分析第一个频率极值点f1的平均值与标准差,得到的实验结果见表 1.

根据表1 的结果可以发现,f1的相对稳定度在10–7量级,与测试得到的相对测距精度大致相等,这与理论分析相一致.说明二次强度调制测距系统可以实现绝对距离的测量,相对测距精度与频率的相对稳定度有关,可以达到10–7量级.

表1 f1 的相对稳定度Table 1.Relative stability of f1.

4.2 测距量程分析

(16)式也可写成如下形式:

在光速c以及空气的等效折射率n确定的情况下,随着待测距离的增大,两个光强极小值点对应的频率间隔将减小.根据(23)式,当待测距离从1 m 变化到100 m,两个光强极小值点对应的频率间隔从150 MHz 变化到1.5 MHz.因此为了满足1—100 m 范围内的测距,所需要的扫频范围需涵盖300—3 MHz 的变化区间,这个扫频范围在目前的实验条件下是可以实现的,这意味着本系统的测距量程可以达到100 m.

为了验证系统在不同待测距离下测距精度的变化,选取几段固定长度的光纤进行重复性测距.我们分别选取等效空间距离为1.57,9.14,23.31,38.79,54.11,64.20,79.67 和100.83 m 长的8 段光纤,对每段光纤进行30 次重复距离测试,分析测距结果的平均值以及标准差,计算相对测距精度,实验结果见表 2.

由表2 可见,随着待测距离从1.57 m 增至100.83 m,测距结果的标准差从1 μm 增至30 μm,但其相对测距精度始终在10–7量级.说明在100 m量程范围内,该测距系统的相对测距精度能够达到10–7量级.

表2 相对测距精度Table 2.Relative distance measurement accuracy.

5 结论

本文提出了二次强度调制系统,利用马赫-曾德尔强度调制器对光信号的二次调制来获取距离与光强的信息.我们搭建了实验系统,获得了探测光强与调制频率的余弦函数关系曲线,与理论推导相一致,并通过摇摆法间接找寻光强极小值点对应的频率,不仅降低了噪声的影响,还提高了测距速度,实现2 kHz 的数据刷新率.二次强度调制系统可以直接测量调制器到目标物体之间的绝对距离,测得的频率稳定度以及相对测距精度都在10–7量级,与理论分析结果一致.实验可实现1—100 m量程内的测距,且相对测量精度始终在10–7量级.综上,二次强度调制测距系统可以实现绝对距离的测量,不仅在测距精度以及测距量程上保留了二次偏振调制测距的优势,还省略掉了很多偏振元器件,系统结构更加简化,应用场景适应性更强.