基于四态协议的半量子密钥分发诱骗态模型的有限码长分析*

詹绍康 王金东† 董双 黄偲颖 侯倾城 莫乃达 弥赏向黎冰 赵天明 於亚飞 魏正军 张智明

1) (华南师范大学信息光电子科技学院,广东省量子调控工程与材料重点实验室,广州 510006)

2) (华南师范大学信息光电子科技学院,广东省微纳光子功能材料与器件重点实验室,广州 510006)

半量子密钥分发允许一个全量子用户Alice 和一个经典用户Bob 共享一对由物理原理保障的安全密钥.在半量子密钥分发被提出的同时其鲁棒性获得了证明,随后半量子密钥分发系统的无条件安全性被理论验证.2021 年基于镜像协议的半量子密钥分发系统的可行性被实验验证.然而,可行性实验系统仍旧采用强衰减的激光脉冲,已有文献证明,半量子密钥分发系统在受到光子数分裂攻击时仍旧面临密钥比特泄露的风险,因此,在密钥分发过程中引入诱骗态并且进行有限码长分析,可以进一步合理评估密钥分发的实际安全性.本文基于四态协议的半量子密钥分发系统,针对仅在发送端Alice 处加入单诱骗态的模型,利用Hoeffding 不等式进行了有限码长情况的安全密钥长度分析,进而求得安全密钥率公式,其数值模拟结果表明,当选择样本量大小为 105 时,能够在近距离情况下获得 10-4 bit/s 安全密钥速率,与渐近 情况下 的安全 密钥率相近,这对半量子密钥分发系统的实际应用具有非常重要的意义.

1 引言

理论上,基于量子物理定律,量子密钥分发(quantum key distribution,QKD)允许两个量子用户—Alice 和Bob 无条件安全地共享一对密钥.QKD 的首个协议[1]在1984 年提出并对其理论安全性进行了充分的证明,之后各种实验方案[2–4]的提出和实际QKD 系统的安全评估的逐渐完善[5,6]证明QKD 的实际可行性.然而实际QKD 系统各环节的技术特性和QKD 理论协议之间存在差别,使得密钥分发过程会受到各种各样的量子黑客攻击[7–16].例如,QKD 普遍使用的光源是强衰减的激光脉冲,这使得密钥分发过程中易受到光子数分裂(photon number splitting,PNS)攻击[7–10]的威胁.此外,针对单光子探测器的具体技术特性,可以展开致盲攻击、探测效率不匹配攻击、后向荧光边信道攻击等[11–16],导致通信双方在不知情的情况下被窃听者窃取密钥信息.为了抵抗针对单光子探测器的攻击,测量设备无关量子密钥分发(MDI-QKD)[17]被提出,随后双场量子密钥分发协议(TF-QKD)[18]和模式匹配量子密钥分发协议(MP-QKD)[19]等能够抵御针对单光子探测器的攻击,同时使传输距离变得更长的协议被提出.由于TF-QKD 在实验上对于实验条件要求较高,许多TF-QKD 的变体[20–23]提出,它们在实验上相较于TF-QKD 比较容易实现.2022 年谢元梅等[24]提出异步MDI-QKD,在TF-QKD 的基础上进一步提高测量设备无关量子密钥分发的传输距离.诱骗态协议[25–30]和单光子类协议——SARG04[31]协议被提出以抵御PNS 攻击,其中诱骗态协议得到了广泛应用.考虑实际应用发送的脉冲数量是有限的,有限码长情况下QKD系统的分析相继完成[32–34],此外Lim 等[35]和Rusca等[36]分别完成了双诱骗态QKD 系统和单诱骗态QKD 系统的有限码长情况下安全密钥速率的分析,并指出有限码长情况下单诱骗态QKD 系统的密钥传输速率相较于双诱骗态QKD 系统有一定的优势.

半量子密钥分发(semi-quantum key distribution,SQKD)在2007 年由Boyer 等[37]提出,它(四态协议,BKM-07)允许一个量子用户Alice 和一个经典用户Bob 安全的共享一对密钥.随后基于实际实现的角度,小于四态协议[38]、镜像协议[39]被提出,这些协议提出的同时,它们的理论安全性得到了证明,尤其是对于独立攻击和集体攻击[40–44],同时也确定了安全比特率.2021 年王金东课题组[45]实现了基于镜像协议的SQKD 实验实现,验证了实际SQKD 系统的实验可行性.与QKD 系统相对应地,SQKD 的理论安全性证明都是基于单光子源进行的,因此实际系统的SQKD 也会受到PNS攻击的威胁.弥赏等[46]在2022 年提出了针对于SQKD 系统的联合PNS 攻击,证明了一定条件下的PNS 攻击能使窃听者Eve 在通信双方没有察觉的情况下窃取信息.与QKD 系统相似,SQKD 系统在密钥分发过程中添加诱骗态能较好地抵抗PNS攻击,因此基于Alice 发送有限脉冲的有限码长安全评估是必要的,传输的脉冲数量过少会导致安全密钥速率过低,需要较多的时间生成安全密钥,使通信效率降低;反之传输的脉冲数量过多会需要较多的光资源,使通信成本提高,因此需要寻找一个合适的样本量大小来获得最佳的安全密钥速率并确定安全密钥速率的大小.

本文首先建立了基于BKM-07 协议的仅量子用户端加入单诱骗态SQKD 系统的模型,随后为该系统提供了有限码长情况下简洁而严密的安全密钥界限: 基于熵的不确定关系和Hoeffding 不等式[47]对有限的传输脉冲数量进行错误估计,推导出针对一般攻击有效的安全密钥界限,它可以通过几个简单的探测事件界限公式进行推导;随后模拟实际探测情况,以Alice 探测响应的数量固定为前提,推导出Alice 需要发送的总脉冲数,进而求出安全密钥率公式并进行数值模拟;最后对数值模拟结果进行了讨论和总结.

2 基于四态协议SQKD 系统的诱骗态模型

本节将会介绍四态协议(BKM-07 协议)的模型,随后提出添加诱骗态的方法并详细说明密钥分发过程.BKM-07 协议的密钥分发过程见图1.

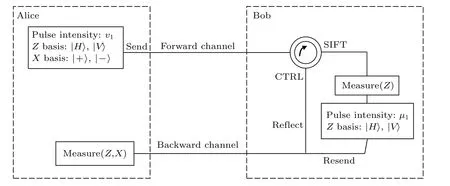
图1 BKM-07 协议模型Fig.1.BKM-07 protocol model.

1) Alice 随机均匀地选择一个比特值并将该值记录到集合yi中,接着,它随机均匀地从X基和Z基中选择一个作为对应比特的基并记录到集合ai,Alice 根据两个集合中位置i的值对光脉冲进行调制,最后将光脉冲发送给Bob.

2) Bob 随机均匀地选择对到达的光脉冲实施SIFT 操作或CTRL 操作,并将所选择的操作记录到集合ci.对于选择SIFT 操作的脉冲,Bob 以Z基进行测量,并将结果记录到集合si,随后根据测量结果,以Z基和脉冲强度µ1在相同位置重发光脉冲;对于选择CTRL 操作的脉冲,Bob 不进行任何操作,将光脉冲反射回到Alice 端.

3) Alice 对返回的每一个脉冲根据自己发送时使用的基进行测量,并将以Z基进行测量得到的结果记录到集合zi,以X基进行测量得到的结果记录到集合xi.

4) Alice 和Bob 在经典信道公布集合ai和ci,随后双方计算响应率及错误率是否符合预期,若不符合预期则认为密钥分发过程被窃听,停止本次密钥分发;若符合预期则生成期望长度的初始密钥执行后处理步骤,最后生成安全密钥.

实际情况中,即便SQKD 系统中包含着天然诱骗态(CTRL 操作),但它仍有可能受到PNS 攻击而导致密钥信息泄露,并且实际情况中生成的初始密钥长度是与各个事件探测响应的数量密切相关的,因此以下将描述诱骗态模型下密钥分发的过程并说明通信双方如何得到长度为l的安全密钥,同时为了进行有限码长分析给出相应的变量定义,如图2 所示.

图2 基于BKM-07 协议的诱骗态SQKD 模型Fig.2.Decoy SQKD model based on BKM-07 protocol.

1) Alice 随机均匀地选择一个比特值并将该值记录到集合yi中,接着,它随机均匀地从X基和Z基中选择一个作为对应比特的基并记录到集合ai,并以概率和1-选择脉 冲强度v1或v2(v1＞v2＞0 )并将数据记录到集合bi,最终Alice根据3 个集合中位置i的值对光脉冲进行调制,随后发送给Bob.

2) Bob 随机均匀地选择对到达的光脉冲实施SIFT 操作或CTRL 操作,并将所选择的操作记录到集合ci.对于选择SIFT 操作的脉冲,Bob 以Z基进行测量,并将结果记录到集合si,随后根据测量结果,以Z基和脉冲强度µ1(µ1＞v1+v2)在相同位置重发光脉冲;对于选择CTRL 操作的脉冲,Bob 不进行任何操作,将光脉冲反射回到Alice 端.

3) Alice 对返回的每一个脉冲根据自己发送时使用的基进行测量,并将以Z基进行测量的结果记录到集合zi,以X基进行测量的结果记录到集合xi.

4) Alice 和Bob 在经典信道公布集合ai,bi,ci,随后双方计算各脉冲强度的响应率是否符合预期,若符合预期则筛选生成由Alice 选择Z基且Bob选择SIFT 操作发送的光脉冲导致测量响应的结果组成的、双方共享的集合SZ,Alice 分别生成由Bob 选择CTRL 操作且Alice 以Z基发送和以X基发送的光脉冲导致测量响应的结果组成的集合CZ和CX;重复步骤1)—步骤3)直到 |SZ|≥nSZ,|CZ|≥nCZ和|CX|≥nCX.

5) Alice 和Bob 从集合SZ中随机选择大小为nSZ的样本作为初始密钥(SZA,SZB),随后Alice根据集合CX估计相应的错误比特数mCX,k,接着它们计算初始密钥中的真空事件sSZ,0和单光子事件sSZ,1,最后它们计算初始密钥中单光子事件的相位错误的数量cSZ,1,并估计实际相位错误率ϕSZ=cSZ,1/sSZ,1,同时判断实际相位错误率是否低于预期值,若不满足则终止密钥分发,若满足则进行步骤6).

6) 首先Alice 和Bob 进行错误校验,假设它们根据预期的相位错误率进行校正,则它们会揭示λEC位信息;接着,它们执行错误验证步骤,确保两者共享相同的密钥,这个过程中它们使用两个通用哈希函数[14],会揭示 log21/εhash位信息,其中εhash是指一对非相同密钥能够通过错误验证步骤的概率;最后,它们对密钥进行隐私放大,提取长度为l的密钥对(SA,SB).

3 有限码长分析

本节将基于第2 节提出的SQKD 模型进行有限码长的安全密钥速率分析,分为4 部分: 安全分析、事件界限、探测和错误模拟、数值模拟.安全分析利用熵的不确定关系推导出以Eve 所获得的信息为条件的原始安全密钥的最小长度公式;事件界限根据密钥长度公式中的项,基于Hoeffding 不等式对所需探测事件的数量进行有限码长情况下的界限值估计;探测模拟和错误模拟将根据模拟分析各类光脉冲的探测概率及各类探测事件之间预期数目的关系;数值模拟将基于光纤通信的信道模型对有限码长分析的结果进行数据模拟.最后对数值模拟的结果进行了详细的讨论.

3.1 安全分析

安全分析主要思路是利用熵不确定性关系来建立以Eve 获得的信息为条件的原始密钥的最小平滑熵的界限.首先,定义E′为窃听者Eve 获得的关于初始密钥SZA的信息,E为经过纠错及错误验证步骤后窃听者Eve 获得的关于初始密钥SZA的信息.使用两个通用哈希函数[48]进行隐私放大可以获得长度为l的εsec-安全密钥:

将SZA分解为即将初始密钥中的各个比特分解成由探测单光子脉冲、空脉冲及多光子脉冲得到的比特,由于Eve 具有光子数分辨能力,因此认为Eve 能执行这种分解.为了方便后面的计算,令误差项v=2α1+α2+(α3+2α4+α5),α1,α2,α3,α4和α5均大于0,随 后应用最小平滑熵的广义链式规则[49]可以得到:

同时,应用熵的不确定性[50]并考虑Eve 通过PNS攻击无法窃取单光子脉冲中的信息,即Eve 关于的确定性不会大于中的错误比特数可得

其中cSZ,1为之间不相同比特的数目,使用文献[51]中给出的无替换结果的随机抽样进行估计,基于超几何分布的近似技术,可以得到下面的不等式以至少的 1-α1概率被满足:

综合以上所有的公式,能够得到密钥长度公式为

其中β为误差项,考虑有限码长情况引入的误差项以及密钥长度公式推导中引入的误差项,设α4=α5=0 可以得到安全性误差εsec为

式中 ,ε1,ε2和ε3均为有限码长情况下引入的误差项,其前面的系数为各自对应的Hoeffding 不等式(10)式、(12)式、(14)式在密钥长度公式中满足的次数.为了得到较好的安全性,令每一个误差项均为同一个值ε,得到εsec=19ε,由于有7 个误差项且 log2(1/β) 为所有误差项对安全密钥长度的影响,最终取β=(εsec/19)7,因此密钥长度公式表示为

3.2 事件界限

本节提供了密钥长度公式中将会使用到的探测事件界限sSZ,0,sSZ,1和ϕSZ的详细信息,界限的分析基于强衰减激光脉冲的泊松分布和Hoeffding不等式结合.由于SQKD 系统中Z基与X基的光脉冲的探测概率显然不同,因此分析中将区分X基与Z基的光脉冲进行分析.

根据诱骗态SQKD 的模型可以得到,从Bob端发送出来的脉冲(不区分SIFT 操作和CTRL 操作)强度的可能值为µ1,ηcv1和ηcv2,令µ2=ηcv1,µ3=ηcv2和K=[µ1,µ2,µ3],根据预先的设定可得µ1≥µ2+µ3,µ2＞µ3≥0,由于每个脉冲只有强度不相同,对于窃听者Eve 而言,无法区分每个脉冲的强度,这使得Eve 即使实施PNS 攻击,通信双方也能察觉.

考虑Bob 以Z为基对脉冲进行编码的情况,并且设sZ,n为Bob 发送Z基下n光子脉冲且Alice探察到的次数为预期Bob 发送Z基光脉冲且Alice 探测到的次数,在渐近极限中,脉冲强度为k的探测次数为

此时考虑一个有限码长的统计场景,可以使用Hoeffding 不等式[47]进行估计.通过Hoeffding不等式可以得到探测到的次数nZ,k与相应渐近情况的之差满足一定约束关系的概率为

与前面的情况类似,对于有限码长统计情况下的约束如下:

接着考虑Bob 以X基对脉冲进行编码而Alice探测结果出现错误的错误率估计.相似地,设vCX,n为Bob 发送X基下n光子脉冲且Alice 探测结果出现错误的次数为预期Bob发送X基的所有光脉冲中Alice 探测结果出现错误的次数,在渐近极限中,脉冲强度为k的探测次数为

类似地,对于有限码长统计情况下的约束如下:

为了找到各个事件的解析解,必须定义条件概率pn|k.通过使用贝叶斯规则和相干态脉冲中光子分布可以得到下式成立:

1)Z基中真空脉冲事件sZ,0的下限.

将(11)式代入具有不同脉冲强度的两个方程可以得到:

其中等式右边的第二项对于µ2-µ3是非负的,因此通过对上式进行重写可以得到sZ,0的下限为

随着µ3趋于0,界限会变紧.

2)Z基中单光子脉冲事件sZ,1的下限.

对于µ1≥µ2+µ3和n≥2 可得以下不等式成立:

将不等式(20)式代入(19)式可得

其中不等式右边的求和项可由下式表示:

将不等式右边的求和项使用(23)式替代并重写后,可以得到sZ,1的下限.

3)X基中单光子脉冲事件sCX,1的下限.

采用与sZ,1的下限估计相同的计算,可以得到:

对于X基中的光脉冲考虑µ2≥µ3和n≥2的情况,因此得到的成立不等式为

同时考虑,对于X基下任意一个脉冲强度的总错误事件的数量都是大于等于相应空脉冲的错误事件的数量,即

综合(28)式、(29)式和(30)式,可以得到sCX,0的上限为

4)X基中单光子脉冲中出现错误的事件vCX,1的上限.

目前为止,所求的各个界限都不适用于实际探测情况的统计,因为各个事件界限不等式中都包含渐近情况下的项,通过使用(12)式、(14)式、(16)式的变式可以解决这个问题,即将以下公式:

令系数cs表示渐近情况下Alice 在Z基中探测到全部事件中Alice 在Z基中探测且Bob 同时选择了SIFT 操作的事件所占的比率,因此可以得到:

其中,cs的值会在3.3 节中讨论并给出表达式.至此,已经求出了密钥长度公式中会使用到每一个安全界限.

3.3 探测模拟和错误模拟

前文中我们的计算模拟均是将Alice 在Z基中探测总数nZ作为固定值进行的,而密钥长度公式中还需要使用到Alice 在X基中探测总数nCX及其探测结果出现错误的数量mCX还有各类事件分配到各个脉冲强度的事件,因此下文中会展示各类事件之间的关系,用于根据nZ推导nCX,mCX等.

式中R为光源的发射频率,概率pZ,det,B,tot表示为

为得到Alice 在X基中探测事件的数量,需要给出对于脉冲强度v1和v2,Alice 选择发送X基且Bob 选择CTRL 操作的概率及相应错误概率分别为

式中,概率Perr为传输过程中由于设置的未对准而导致的错误概率.类似于(48)式,可以得到强度为µj引起的错误事件:

由概率的可加性,可以得到Alice 在X基下探测事件nCX及相应错误事件mCX可以表示为

因此,为了获得样本大小nZ所需要Alice 发送的脉冲总数Ntotal可以由下式得出:

最后,取密钥长度(10)式与发送的脉冲总数Ntotal的比值,得到每个脉冲的密钥率为

3.4 数值模拟

模拟中考虑了一个基于光纤的SQKD 模型,该模型借用了诱骗态SQKD 和我们实验室中单光子探测器的参数.表1 为在0.1—1.0 范围内,取0.01为步进的所有值作为脉冲强度µ1,v1,v2的取值进行多次模拟得到的0—50 km 的传输距离中每5 km 处能取得最大安全密钥率的各个脉冲强度值,可以发现µ1取 0.68,v1取0.48和v2取0.07 在大部分情况下能够取得最大安全密钥率,因此对于光脉冲生成与调制系统,考虑Alice 端生成的光脉冲强度v1,v2分别为0.48 和0.07,Bob 端生成的光脉冲强度µ1为0.68,脉冲频率为R=1 GHz,Alice和Bob 均以相同的概率发送强度v1或v2的光脉冲和选择SIFT 操作或CTRL 操作.假设光纤具有0.2 dB/km 的衰减系数,即光纤的透过率为ηC=(L为传输长度).探测系统中,设置单光子探测器 的暗计 数概率PDC=10-8,死时间tDT=100 ns,经过光纤传输后由于光学误差引起探测错误的概率Perr=10-2.与参考文献相同,考虑参数λEC为一个简单的函数fECeobs[23],其中fEC为纠错效率,eobs为观察到的Z基中SIFT 操作的事件的错误率的平均值,实际应用中λEC应为实际公布的比特位数;对于保密性参数εsec和正确性参数εcor与文献[13]中一致,分别假设为εsec=10-9和εcor=10-15.

表1 50 km 传播距离中每5 km 处取得最大安全密钥率时脉冲强度 µ1 ,v1 ,v2 的取值和得到的安全密钥率Table 1.Pulse strength µ1 ,v1 ,v2 and the number of Secret key ratio every 5 km in a 50 km transmission distance.

图3 为根据以上密钥分发模型与计算公式绘制的安全密钥率与光纤长度的关系.由图3(a)可以看到,在有限码长的影响下,即便是在近距离传输的情况下,诱骗态SQKD 的最大安全密钥速率能够达到约 10-3量级,相较于 诱骗态QKD 的10-2量级小了约1 个数量级,并且诱骗态SQKD的安全密钥率随着光纤长度的增长而衰减的速率更快,这是因为SQKD 中能够成码的SIFT 操作脉冲还有Bob 重发时光脉冲时由于脉冲强度较小而产生大量空脉冲引入的衰减,该衰减是QKD 系统无需考虑的.这一项衰减使得对于相同的样本量nZ,诱骗态SQKD 能够生成的安全密钥少且需要Alice 发送的脉冲总数多,进而导致安全密钥率小.但是由于SQKD 系统的其中一方为经典方,通过集成化能够使得这一方的通信设备小巧便携,这使得诱骗态SQKD 系统即便安全密钥速率较低,但是在近距离的情况下仍有重要的应用价值.

图3 (a)使用1 GHz 的脉冲 频率时不同码长 nZ 之间的安全密 钥率的比较,nZ 的取值为10s (s=[4,5,6,7]),当nZ=105时安全密钥速率与渐近情况的安全密钥率相近,安全密钥率随光纤长度的增长而急剧衰减,但在约30 km 内能够保持10–5 的安全 密钥率;(b)考虑1 GHz 的脉冲频率时三种不同 nZ 之间近距离安全密钥率的比较,nZ 的取值为 10s (s=[5,6,7])Fig.3.(a) The comparison of secret key rate of different key sizes nZ,when using the pulse frequency of 1 GHz.The value of nZ are 10s (where s=[4,5,6,7]).When 105 is chosen to be nZ,the secret key rate is close to the asymptotic limit’s.The secret key rate decreases sharply with the increase of fiber length,but it can maintain a secret key rate of 10–5 for about 30 km;(b) the comparison of the proximity security key rates between six differentnZ when considering a pulse frequency of 1 GHz.The value of nZ are 10s (where s=[5,6,7]).

图3(b)中绘制近距离情况下诱骗态SQKD 的密钥速率图,由于从图3(a)中可以发现,当样本量nZ选择为104时,近距离情况下的安全密钥率相比于渐近情况具有较大的衰减,而当样本量nZ选择大于104时,近距离情况下的安全密钥率与渐近情况的安全密钥率十分贴合,故我们认为 104对于nZ并不是合适的大小,在考虑绘制近距离情况下安全密钥率与光纤长度的关系图时不考虑nZ=104.发现在大部分样本量中,诱惑态SQKD 能够在70 km 长的光纤中保持 10-5量级以上的安全密钥率,而在GLLP 理论验证得到的渐近情况下SQKD的安全传输距离[52]仅有2 km,相较之下说明诱惑态的加入一定程度上增长了传输距离.从图3(b)可以看出,近距离情况下,渐近情况下的安全密钥速率仅约为nZ=105时的安全密钥速率的1.14 倍,因此实际应用中为避免消耗较多的资源,选择样本量nZ=105比较合适.当考虑nZ=105时,在近距离情况下可以得到约为 10-4bit/s 的安全密钥率,若对应于 1 GHz 的光源重复频率可以得到每秒钟可以产生约105个安全比特.对于实际场景中传输约为几千比特的常规的指纹信息量,采用一次一密的无条件安全加密方式,只需要 ms 级别的时间即可.此外,应用到量子数字签名中,10-4bit/s 的安全密钥率能够在极短的时间内保证OTUH-QDS协议[53]中Alice 与Bob 和Charlie 分别生成两对密钥,随后Alice 利用这两个密钥进行异或操作生成与Bob 的不对称密钥进行量子数字签名,同时由于经典方的设备可以做得易于携带,这使签署方轻易快速地与较多人完成安全性签署成为可能.

4 结论与展望

本文首先描述了基于四态协议的SQKD 诱骗态模型,随后基于该模型对有限码长情况下SQKD系统的安全密钥率进行了分析与数值模拟,最终发现,设定探测到的Z基下光脉冲数量为 105可以得到与渐近情况相近的安全密钥率,意味着实际应用中,只需设定Z基下探测到的光脉冲数量为 105便可获得与理论情况相近的安全密钥率,其中最坏情况下,实际安全密钥率为理论的0.87 倍.还发现安全密钥率在近距离情况下保持较好的安全密钥率,详细地说,在距离小于20 km 的情况下基于四态协议的SQKD 诱骗态模型能保证 10-4量级的安全密钥率,这证明了实际近距离情况下诱骗态SQKD系统进行信息传输、交换的可行性.由于经典方Bob的设备要求较低,分析中也并未限制Bob 的个数,并且多个经典方的SQKD 系统的鲁棒性也已得到证明[54],所以我们认为本文的分析对未来实现同一个Alice 端与不同Bob 端使用SQKD 系统进行信息交换,如指纹信息交换进行身份认证和生成量子数字签名的非对称密钥等实际应用具有积极意义.

正如前文所说,有限码长情况下诱骗态SQKD的安全密钥率较低是因为Bob 重发光脉冲时空脉冲占比较大导致的.实际中,Bob 对于一个脉冲测量之后重发会导致密钥分发过程不安全,这不是我们希望的,因此后续会继续考虑基于镜像协议、随机调制再生光脉冲强度的镜像协议实验对诱骗态SQKD[45]进行有限码长的分析.针对于Alice 使用多个诱骗态以及Bob 再生新光脉冲时加入一个或多个诱骗态的各种情况,这也包括两端都不加入诱骗态的情况,本文未进行分析,我们会将对密钥分发过程使用诱骗态的个数进行优化作为后续工作.