基于广义似然比引导VMD的港口起重机轴承故障诊断方法
2023-12-01冯文宗张建群孙远韬秦仙蓉
冯文宗, 张 氢, 张建群, 孙远韬, 秦仙蓉
(同济大学 机械与能源工程学院,上海 201804)
滚动轴承是港口机械中不可或缺的部件,其正常运转是维持港口生产运输的重要保障。然而,轴承在发生故障的早期阶段,产生的周期性冲击信号较为微弱,易被强噪声信号掩没,传统的谱分析方法难以实现故障识别,因此信号需要进行信号分解处理。
Huang等[1]提出了经验模态分解方法(empirical mode decomposition,EMD),该方法能够自适应完成信号分解。但是EMD存在模态分量有模态混叠和端点效应,且该方法的独特的递归分解方式没有可释性。Gilles[2]提出了经验小波变换(empirical wavelet transform,EWT),EWT通过小波提取对信号进行分解,该方法具有完备的理论基础,且有效地抑制了模态混叠现象。但是该方法分解结果容易受到噪声干扰,缺乏自适应性。为解决EMD的不足,Dragomiretskiy等[3]提出了变分模态分解(variational mode decomposition,VMD)。该方法以各个模态分量分解的频率之和最小为目标,分解结果稳定,既解决了EMD的模态混叠和端点效应问题,也克服了EWT的缺点。Sharma等[4]成功将VMD算法应用于齿轮箱的齿轮局部故障诊断,试验结果表明VMD的故障检测性能优于EWT。然而,VMD在进行分解前需要进行初始参数设置,不同的初始参数设置组合对应着不同的信号分解结果,对后续分解信号的分析产生重大的影响。为此,众多学者开展了优选VMD参数研究,以期获得VMD的良好自适应性;其关键是优化目标的选取。
王奉涛等[5]提出了计算分量信号能量与原始信号总能量的分解数k的故障诊断方法,成功应用于滚动轴承内圈微弱故障特征提取。韩朋朋等[6]提出了以增强包络谱为目标的优化算法,在全寿命轴承退化数据中识别出轴承的早期故障。郑圆等[7]提出了以最大谱峭度的方法确定分解层数k,该算法能在多振源信号中提取到微弱故障特征频率。胡以怀等[8]提出了基于多尺度排列熵的VMD分解,并将分解信号输入SVM的空压机故障辨识方法,能有效地识别空压机故障类型。张伟等[9]提出了一种基于峭度、功率谱和相关系数的复合影响指数,能够有效避免周期谐波、随机冲击和背景噪声的干扰,但是在强噪声干扰分解效果不太理想。
由上可见,大部分的优化VMD的目标函数可以分为几种类型:第一类是用来检测信号的冲击性(如峰度、峭度);第二类是检测信号的循环平稳性(如谱峭度,增强包络谱);第三类是检测信号的复杂程度(熵),以及前几类指标的组合。轴承在失效的过程中,其产生的振动信号的冲击性、循环平稳性和复杂程度均会发生变化,所以上述目标函数能在一定程度上检测到故障。然而这些目标函数不仅仅对会对故障敏感,实际工作环境中,复杂工况下的噪声和其他组部件的强周期性脉冲振动干扰同样会使这些目标函数发生变化。因而,在强背景噪声下,采用上述目标函数诱导VMD分解极难获得理想结果。
Antoni等[10]提出了一种统计指标IGGCS/GGS。该指标通过两个嵌套的统计模型反映出信号的循环平稳性和冲击性。Ni等[11]提出了以IGGCS/GGS最大值为目标确定分解模态数k,再用故障特征幅度比(ratio of fault characteristic amplitude,RFCA)来确定惩罚参数α的VMD算法,该算法成功实现了微弱故障特征增强,但是忽略了分解模态数k与惩罚参数α存在参数耦合现象。
本文依据统计指标IGGCS/GGS存在的优点,提出一种以统计指标IGGCS/GGS为目标函数VMD分解算法和一种基于统计指标IGGCS/GGS的故障指标故障频率比(ratio of fault frequency,RFF)。该算法同时对模态数k与惩罚参数α在预设范围内进行网格搜索,获得最优初始参数组合和对应最佳模态分量。对最佳模态分量进行RFF指标计算并依据阈值判定实现故障诊断。通过仿真信号、公开数据集和港口起重机故障轴承数据验证。
1 变分模态分解和统计指标IGGCS/GGS
1.1 变分模态分解
变分模态分解能够自适应地把原信号分解为一系列的一系列最小带宽和的本征模函数(intrinsic mode function,IMF)。每一个IMF都是具有不同的中心频率的调幅调频信号。
假设分解原始信号f的所获得的IMF数量为K。则构建的变分约束模型为
(1)
式中:f为原始信号;uk为第k个模态分量;ωk为第k个模态分量的中心频率;*为卷积算子。
为了获取变分约束模型的最优解,引入二次惩罚因子α和拉格朗日算子λ(t),增广拉格朗日函数表达式为
(2)
使用乘法交替方向法(alternate direction method of multipliers,ADMM)算法,不断依次更新uk,ωk和λ,当满足迭代终止条件时,才会结束整个循环,最终得到K个IMF分量。
具体实施步骤如下:
步骤1初始化
步骤2更新计数
n←n+1

步骤4更新ωk
步骤5更新λ
步骤6判断是否满足收敛条件
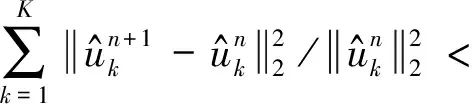
若未满足收敛条件,则跳转至步骤2;
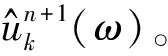
1.2 广义高斯平稳分布模型和广义高斯循环平稳分布模型
在轴承工作的过程中,部件间的相互作用会使产生的振动信号同时兼具有冲击性和循环平稳性。广义高斯平稳分布(generalized Gaussian stationary,GGS)模型可以很好的描述振动信号的冲击性。广义高斯平稳分布模型的概率密度函数可以描述为
(3)
式中:P为概率密度分布;Γ(·)为Gamma函数;β0为形状参数,较小的β0代表分布的冲击性较大;η0为尺度参数,控制信号的方差。
广义高斯平稳分布注重于振动信号的冲击性,但是忽略了振动信号的循环平稳性,Antoni等提出了一种广义高斯循环平稳分布模型(generalized Gaussian cyclostationary stationary,GGCS),其概率密度函数为
px[x(n+k×N);β1,η1(n)]=
(4)
式中:N为每个周期的样本数;n=0,1,…,N-1;k=0,1,…,K-1,K为信号中的基于N的循环周期数;β1为形状参数;η1(n)为N维尺度参数。
与广义高斯平稳分布的尺度参数η0相对比,广义高斯循环平稳分布的尺度参数η1不是一个数,而是N维数组。广义高斯循环平稳分布中一个周期的不同位置的点服从不同的分布,但是不同周期中的相同位置的点服从相同的分布。当广义高斯循环平稳分布中的尺度参数η1数组中所有值都相同时,可以将其视为一种广义高斯平稳分布。信号的循环平稳性为信号的统计特性具有非平稳性,但是随着时间的变化统计特性会产生周期性平稳变化。若信号服从广义高斯平稳分布模型,即x(n)~Px[x(n);β0,η0],则信号中每一个点都服从广义高斯平稳分布模型的概率密度函数且相互独立。其统计特性不会随着时间或者周期的变化而变化,因此该信号不具有循环平稳特性,只具有冲击性。若信号服从广义高斯循环分布模型,即x(n)~Px[x(n+k×N);β1,η1(n)],则信号中的点的分布会随时间而变化,但每个周期中对应的点具有相同的分布,因此该信号具有循环平稳性。故高斯循环平稳模型既能够表达振动信号的冲击性,也能够有效的描述振动信号的循环平稳性,
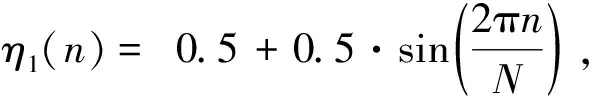
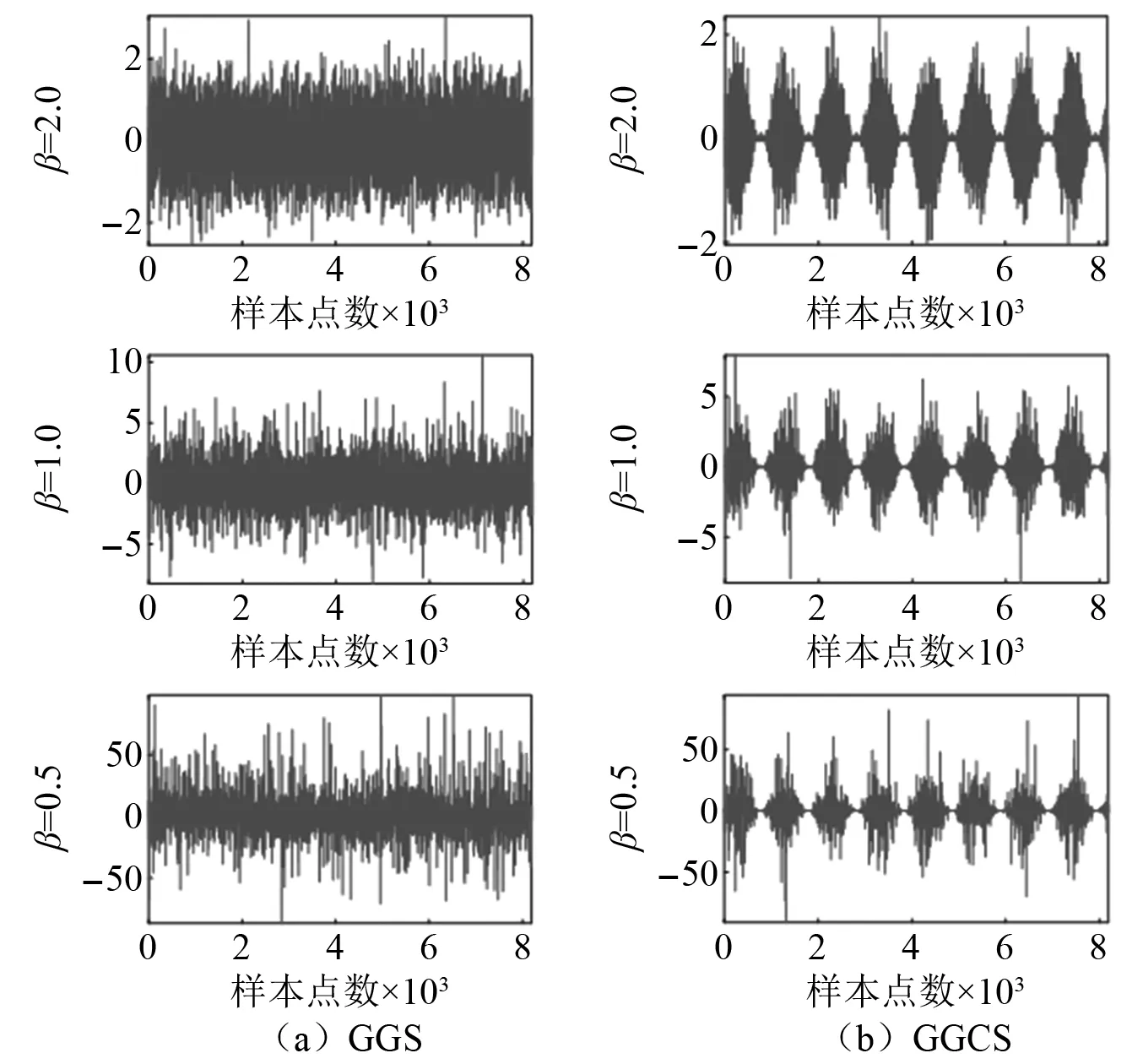
图1 不同的参数下GGCS和GGS模型的仿真信号Fig.1 Simulation signals of GGCS and GGS models with different parameters
1.3 统计指标IGGCS/GGS
假设H1和假设H0分别代表振动信号服从不同的概率密度函数。
(5)
为了判断两个假设中哪一种假设能更加准确地描述测量信号,采用广义似然比(generalized likelihood ratio,GLR)来判断信号服从何种假设,广义似然比可以表示为
(6)
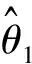
由于广义似然比难以求取,对式(6)等式两边取对数可得对数似然比

LH1(x)-LH0(x)
(7)
依据对数似然比,Antoni等提出了一种统计指标IGGCS/GGS。在统计指标IGGCS/GGS中,假设H0表示振动信号服从广义高斯平稳分布,H1表示振动信号服从广义高斯循环平稳分布。统计指标IGGCS/GGS可以定义为
(8)
式中:l为振动信号长度;LGGS为服从广义高斯平稳分布的极大似然;LGGCS为服从广义高斯循环平稳分布的极大似然。LGGS和LGGCS的求解公式分别为
LGGCS=llnβ1-lln2-
(9)

(10)
对1.2节的不同参数下的GGCS和GGS模型的仿真信号进行统计指标IGGCS/GGS估计,结果如图2所示,图中横坐标为预估的周期点数循环周期点数N,搜索区间为[1 004,1 044]。可以很明显观察到,三个GGCS模型在循环周期点数N=1 024时,其统计指标IGGCS/GGS数值最大。信号的统计指标IGGCS/GGS值越大表示该信号更可能服从广义高斯循环平稳分布,越小表示该信号更可能服从广义高斯平稳分布。

图2 GGCS和GGS模型的仿真信号在不同循环周期 点数统计指标IGGCS/GGS值Fig.2 Statistical indicators IGGCS/GGS values for the simulated signals of GGCS and GGS models at different cycle points
2 所提的算法
2.1 基于统计指标IGGCS/GGS引导的变分模态分解算法
故障轴承在工作过程中会产生周期性冲击信号成分,该信号成分既具有循环平稳性,又具有冲击性,会更加符合广义高斯循环平稳分布。信号的统计指标IGGCS/GGS值越大表示该信号更服从广义高斯循环平稳分布,越有可能包含轴承故障信息成分。基于统计指标IGGCS/GGS和故障成分特点,本文提出一种追踪可疑故障频率的基于统计指标IGGCS/GGS的变分模态分解算法,流程图如图3所示。具体实施步骤为:
步骤1确定可疑故障频率ff和统计指标IGGCS/GGS相关参数。根据旋转频率fr估算可疑故障频率ff(共nmax个),计算出在采样频率fs下故障频率ff对应的周期点数N0,N0=round(fs/ff),round为取整函数。因为计算N0与实际N0略有差异,本文建议设置一个检索区间Q,在[N0-Q,N0+Q]中寻找IGGCS/GGS最大的点作为实际循环周期点数N。本文中Q为设定为8。
步骤2确定VMD初始参数组合k和α的检索区间。本文中k检索区间为[2,12],α的检索区间为[1 000,4 000][12]。n=1。
步骤3以IGGCS/GGS为目标函数对VMD初始参数组合进行网格搜索。对信号进行基于可疑故障频率ffn的VMD初始参数组合k和α在检索区间中进行网格搜索,依据经验,本文设定k和α的步长分别为1和100。目标函数为VMD分解后所有模态分量(IMFs)的IGGCS/GGS中的最大值。获取基于可疑故障频率ffn最优VMD初始参数组合kop和αop。
步骤4计算最优模态分量IMFop和最优周期点数Nopn。对信号进行kop和αop的VMD分解,获得kop个IMFs,选取模态分量中IGGCS/GGS值最大的模态分量最为最优模态分量IMFop。选取IMFop的最大IGGCS/GGS的循环周期点数N为最优周期点数Nopn。
步骤5计算其RFF指标,判断是否发生故障。感觉IMFop计算其RFF指标(见2.2节),并根据阈值判断是否发生可疑故障频率ffn下故障。
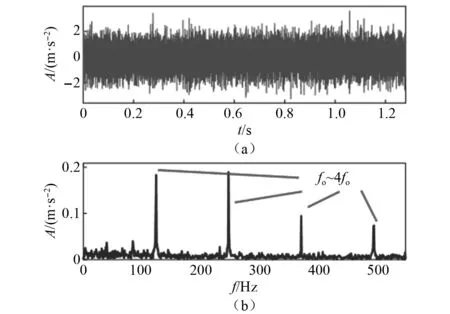
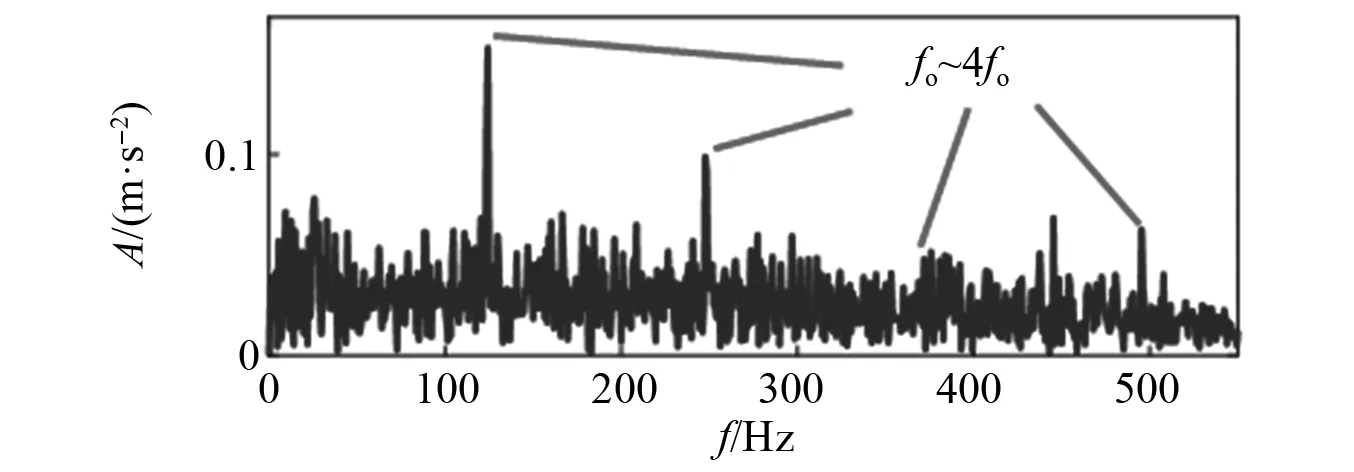
步骤6判断是否满足循环条件。若n 在使用IGGCS/GGS指标完成对基于可疑故障频率ff的VMD的参数优化后,可以获得IGGCS/GGS指标的最优周期点数Nop。本文针对本文所提出的VMD优化方法,提出了一种故障指标故障频率比,具体公式为 (11) 式中:HES(n)为信号x(t)的包络谱,HES(n)=|FFT|Hilbert(x(t))||;k′为倍频数; 故障指标RFF通过故障频率及其倍频频带谱线和其周围谱线的均方的比值进行判断,故障指标RFF的值能够反应出其中特定信号谱线在包络谱中是否明显。其原理为若信号中包含目标故障信息,则故障频率及其倍频频带所包含的能量会相比较周围谱线所包含能量相比会更大。故障的生成是一个连续的过程,随着故障不断地扩大,故障频率及其倍频频带所包含的能量也会不断地增大。本文经过多次试验尝试,发现在大部分正常信号RFF值会小于1.9,大部分故障信号的RFF值会大于2.2。因此在本文推荐设置故障阈值为2,并在后续试验中设定故障阈值为2。当RFF>2时,则判定该信号在存在此故障频率下的故障。RFF<2时,则判定该信号暂未存在此故障频率下的故障。 为了验证本文所提出方法的可行性,建立滚动轴承故障模型[13]模拟旋转机械运行中的外圈故障产生的冲击信号。为了模拟机械系统的复杂工况,对滚动轴承故障模型添加强烈高斯白噪声,滚动轴承故障模型仿真信号为 式中:A0为故障冲击振幅,A0=0.5;fr为转频,fr=25 Hz;C为衰减系数/阻尼系数,C=800;fBPFO为外圈故障频率,fBPFO=120 Hz;T1为外圈故障周期T,T1=1/fBPFO;τκ为第K次冲击相对于周期T1的微小波动,服从0均值正态分布,标准差为转频的0.005%;n(t)为高斯白噪声成分,本模型中信噪比设为-16 dB;采样频率fs=25 600 Hz,采样时长为1.28 s。分析点数为32 768点。 滚动轴承故障模型原始仿真信号和添加噪声后的仿真信号时域波形、频谱和包络谱,如图4所示。从图4(a)中可以看出,从原始仿真信号时域中能够较好地观测到周期性的外圈故障冲击,在频谱和包络谱上也能清晰的观测到旋转频率、外圈故障频率和外圈故障频率倍频。但在图4(b)中周期性故障冲击被噪声完全淹没,频谱和包络谱上旋转频率和外圈故障频率成分无法进行有效区分。 图4 仿真信号的波形和谱图Fig.4 Waveform and spectrum of the simulated signal 使用本文提出的方法对加噪后的仿真信号进行研究。首先估计仿真信号的旋转频率fr=25 Hz,对应转速下轴承的外圈故障率估算为fBPFO=120 Hz。对应的循环周期点数N计算为fs/fBPFO=213。设置检索区间Q=8,则循环周期点数N检索区间为[205,221]。对VMD参数k和α在区间[2,12]和[1 000,4 000]上进行基于IGGCS/GGS最大值网格搜索。搜索结果如图5所示。获得VMD最优初始参数组合k=11,α=2 800。 图5 IGGCS/GGS最大值网格搜索结果图Fig.5 Graph of IGGCS/GGS maximum grid search results 对故障模拟信号进行基于最优初始参数组合的VMD分解,最优模态分量为IMF9。根据IMF9的计算RFF故障指标,得到RFF=2.702,大于设定阈值2,故判定该轴承发生了外圈故障。IMF9包络谱如图6所示,明显观测到旋转频率、外圈故障频率和其倍频,证明故障指标RFF的准确性。 图6 基于最优参数VMD分解后VMF9的频谱与包络谱Fig.6 Frequency spectrum and envelope spectrum of VMF9 after VMD decomposition based on optimal parameters 为了验证说明本文所提出方法对实际信号的有效性,选取XJTU-SY滚动轴承加速寿命试验[14]中的Bearing3_1数据集作为研究对象。如图7所示,该试验台主要由交流电动机、电动机转速控制器、转轴、支撑轴承、液压加载系统和测试轴承等组成。试验台的轴承想好为LDK-UER204滚动轴承。Bearing3_1数据集实在工况3(1 200 r/min,10 kN)下进行测试,其总寿命周期为42 h 18 min,最终失效位置为轴承外圈。全寿命周期中共有2 538组数据。信号分为两个通道:通道1为水平方向振动加速度传感器采集到的信号;通道2为竖直方向振动加速度信号采集到的信号。因为该试验台液压加载系统是在水平方向为试验轴承添加工作载荷,通道1信号对轴承失效更加敏感,所以选取通道1信号为研究对象。 图7 XJTU-SY滚动轴承加速寿命试验试验台示意图Fig.7 Schematic diagram of XJTU-SY rolling bearing accelerated life test bench 使用均方根(root mean square,RMS)指标来分析轴承寿命退化趋势,对全寿命周期中2 538组数据进行均方根统计指标计算,结果如图8所示。明显观测到图8中第2 385组信号样本后增长速度明显上升。在轴承故障发生后,信号的均方根统计指标会有明显的上升[15],故判定轴承在第2 385组处产生故障。选取第2 401组数据通道1信号作为本文的研究对象。根据轴承型号和试验台工况计算出试验台轴承的故障特征频率,结果如表1所示。该信号时域波形和包络谱如图9所示。在图中可以明显观测到,外圈故障频率123.3 Hz及其倍频,说明试验台中轴承外圈已经发生故障。 表1 LDK UER204轴承特征频率相关估计值 图8 全寿命振动信号RMS值Fig.8 RMS value of full life vibration signal 图9 第2 401组数据通道1信号时域波形和包络谱Fig.9 Time domain waveform and envelope spectrum of the signal of data channel 1 of group 2 401 考虑到实际工况中存在强干扰,对试验信号添加-10 dB高斯白噪声和强周期脉冲信号。强周期脉冲信号时域波形和包络谱如图10(a)所示,其频率为100 Hz。图10(b)为添加强干扰噪声后的信号谱图,难以识别出旋转频率及故障频率。 对强干扰噪声后的第2 401组数据通道1信号用本文的所提出的算法进行分析,对其挑选出的最佳模态分量进行故障指标RFF分析,其结果如表2所示。由表2可知,第2 401组数据中除了轴承外圈故障频率的RFF值大于设定阈值2,其余轴承故障频率的RFF值都小于设定阈值。判定第2 401组数据存在外圈轴承故障,诊断结果与数据集实际结果契合。 表2 第2 401组数据通道1信号各故障分析结果 为了验证RFF的准确性,取基于轴承外圈故障下的分解结果进行验证。算法所得到的最优初始参数组合为kop=12和αop=2700,最佳模态分量为IMF12,对应最佳周期点数Nop=207,最佳估算频率为123.67 Hz。对最佳模态分量进行包络谱分析,结果如图11所示。从谱图上可以很明显看出,故障特征频率的及其倍频,因此提出的算法能够有效的抑制强周期脉冲信号的干扰,实现微弱故障提取和故障诊断。 图11 第2 401组数据通道1信号(-10 dB) 最佳模态分量包络谱Fig.11 Best modal component envelope spectrum of the signal of data channel 1 (-10 dB) of group 2 401 本文采用另一种的算法[16]与本文提出算法进行对比。该算法采用包络熵和包络谱峭度作为目标函数对信号进行变分模态分解,之后选择样本熵最小值作为最优模态分量。对相同信号进行最优初始参数组合求解。其最终优化结果是最优初始参数组合为kop=6和αop=1 845,最佳模态分量为IMF6,最佳模态分量包络谱如图12所示。在包络谱中能够提取出强周期干扰信号频率及其倍频,但是未能有效提取出实际故障特征。 为了验证说明本文在实际运转情况下的问题,对南沙某港港口起重机起升机构的实际信号[17]进行分析研究。该港口起重机起升机构主要由电机、齿轮箱和卷筒组成,通过电机驱动齿轮箱,齿轮箱带动卷筒上线缆运动实现港口集装箱升降。该起重机传动系统实物图和示意图分别如图13所示,图13(b)中数字表示振动加速度信号采集器位置分布。采样频率为51 200 Hz。 图13 港口起重机抬升机构Fig.13 Harbor crane lifting mechanism 日常巡检中发现驱动电机处发出异响,疑似电机端轴承发生故障。轴承型号为斯凯孚公司的23232 CC/W33。取港口起重机起升机构通道2中的一段平稳信号作为研究对象,信号时域波形和包络谱如图14所示,电机轴的旋转速度约为1 180 r/min。依据该轴承型号和转速估算轴承的故障特征频率,结果如表3所示。 表3 23232 CC/W33轴承特征频率Tab.3 23232 CC/W33 bearing characteristic frequency 对信号使用本文的所提出的算法进行分析,对其挑选出的最佳模态分量进行故障指标RFF分析,其结果如表4所示。由表可知,通道2信号中除了轴承外圈故障频率的RFF值大于设定阈值2,其余轴承故障频率的RFF值都小于设定阈值。判定通道2信号存在外圈轴承故障。 表4 港口起重机抬升机构通道2信号各故障分析结果 经过维护检测后发现轴承外圈发生故障,故障轴承如图15所示,这验证了所提RFF指标的有效性。其分解信号的包络谱图如图16所示,其故障频率及其二倍频和三倍频较为明显。 图15 故障轴承部位Fig.15 Faulty bearing part 图16 港口起重机抬升机构通道2信号 最佳模态分量包络谱Fig.16 Best modal component envelope spectrum of channel 2 signal of port crane lifting mechanism 通过本文的研究,得到以下结论: (1)提出了基于一种基于统计指标IGGCS/GGS为目标函数VMD初始参数组合优化的方法,通过多个试验可以证明,用该方法分解的得到最优模态分量能够实现强噪声情况下的故障特征提取。 (2)提出了一种基于统计指标IGGCS/GGS的故障指标RFF,该指标与上述算法结合能够有效的实现微弱故障诊断。 需要指出的是,尽管所提方法能够有效地诊断微弱故障,但是所提方法需要对可疑故障频率进行预先设定,不能自适应检索故障频率。未来,将尝试解决这一问题。2.2 故障指标故障频率比指标RFF
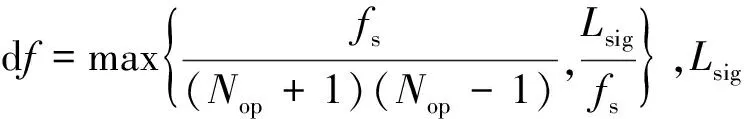
3 试验验证与分析
3.1 仿真信号分析


3.2 试验数据集信号分析




3.3 港口起重机实际数据验证





4 结 论
