叠加阀片式减振器建模与结构参数优化

2023-12-01黄彩霞王建德吴晨曦

振动与冲击 2023年22期

黄彩霞, 伍新, 舒雄, 王建德, 吴晨曦

(1. 湖南工程学院机械工程学院,湖南湘潭 411104;2. 长沙理工大学机械装备高性能智能制造关键技术湖南省重点实验室,长沙 410114)

作为汽车悬架重要部件的减振器,其参数匹配与优化一直是改善平顺性、操纵稳定性的重要措施[1-2]。当前很多汽车企业仍采取试验方法对新研发车辆进行减振器匹配。在该方法中,通过安装不同的减振器进行实车试验,借助平顺性和操纵稳定性的客观和主观评价,最终确定适合的减振器[3-4]。另一方面,在减振器开发过程中,一般仍借助传统的设计方法,即通过反复的设计制造、试验分析、改进等过程,从而导致开发周期长,研制成本高等缺陷。因此,如何借助计算机辅助计算、设计、分析等先进设计手段,对加快减振器开发至关重要[5-7]。

减振器主要是通过阻尼特性或示功特性影响悬架的性能[8-9],其数学模型是车辆动力学建模、阻尼特性分析和参数优化的基础,主要包括基于减振器结构参数的物理模型,以及仅能描述阻尼特性的非参数数学模型。其中,基于减振器物理模型主要是基于流体动力学理论,首先建立液体流进节流孔、阀片缝隙等阻尼原件时的压力损失,最终获得阻尼力关于速度的特性曲线。建模手段包括解析模型的数值计算法、基于商业软件的原件计算法、有限元计算法等。如考虑常通孔和锥形圆环缝隙产生阻尼力的机理,建立减振器开阀速度、阀片打开后常通孔流量、阀片动态开度的数学模型[10]。联合有限体积法和有限元法对减振器流—固耦合模型进行求解和分析,建立的流—固耦合模型,或利用AMESim的液压元件库,搭建减振器的压缩气体、活塞缝隙、常通节流孔等液流通道,解析阻尼力产生机理[11-12]。非参数数学模型是减振器的阻尼特性模型,不涉及减振器具体的结构参数。模型参数通过对阻尼特性数据进行拟合而辨识出,常用于在车辆动力学模型中产生悬架的阻尼特性。叠加阀片式减振器通过改变节流阀片数量、厚度,或选择不同垫圈直径来改变阻尼特性,具有参数调整灵活、阻尼特性非线性好等优点,已成为高档汽车的减振器首选形式。但由于叠加阀片刚度非线性强、液流通道复杂等因素,增加了这种减振器的建模难度[13]。

为了获得最佳的乘坐舒适性或操纵稳定性,需要对减振器数学模型的参数进行优化。针对非参数数学模型,在给定的优化目标函数下,优化阻尼特性曲线拟合多项式的系数[14],或分段线性阻尼的关键参数[15]。如果仅考虑减振器的线性阻尼特性,可直接优化减振器的阻尼系数[16-18],或阻尼比[19]。减振器阻尼特性参数并不直接对应减振器的结构参数,对减振器设计与加工不具有指导意义。如果要对减振器的结构参数进行优化,必须基于减振器的物理模型设置结构参数为设计变量,如常通孔径、卸荷孔径等[20]。由以上研究成果可知,研究成果将减振器阻尼特性参数和结构参数的优化完全割裂,且仅针对减振器的简单结构参数开展优化。另外,将减振器阻尼特性线简化为线性参数的方法,无法准确反映减振器的非线性阻尼特性。由于减振器阻尼特性曲线参数与减振器结构参数之间没有直接对应关系,如何根据悬架性能获得最优的减振器阻尼特性参数,进而反求出结构参数,才是车辆悬架设计与优化的关键。本文在建立减振器高精度数学模型的基础上,以最优阻尼特性曲线为目标和桥梁,开展减振器的结构参数优化设计,并通过试验检验优化结果的有效性。

1 叠加阀片式减振器的液流通道

减振器是车辆悬架中的减振耗能元件。当车轮与车身之间的距离减小时,活塞迫使压缩腔的油液通过复原阀进入复原腔,另一部分油液通过压缩阀进入储油腔;当车轮与车身之间的距离增大时,活塞迫使复原腔的油液通过复原阀进入压缩腔,活塞杆所占体积由储油腔的油液补充。油液通过减振器的复原阀和压缩阀时会产生阻尼力。油液在流动时将振动的动能转化为热能,实现能量的耗散。由此可见,油流通道是产生阻尼力的关键因素,减振器的物理模型是对各液流通道的建模。

在减振器的复原行程中,活塞向上运行,复原腔的油液通过活塞组件向下流动,液流通道如图1(a)所示。油液通过复原阀盖板与活塞筒之间的环形通道进入叠加阀片的缝隙,然后经过活塞上的常通孔进入流通阀。在活塞上、下腔压差作用下,流通阀克服弹簧作用形成平面流通通道。油液流经活塞常通孔后通过平面流通通道和流通阀上的常通孔进入压缩腔。由于叠加阀片的缝隙较小,所以能产生较大的阻尼力。

图1 复原和压缩行程的液流通道Fig.1 Fluid flow channels for rebound and compression strokes

在减振器压缩行程中,活塞向下运行,复原腔的油液通过活塞组件向上流动,液流通道如图1(b)所示。在活塞上、下腔压差和流通阀片压紧弹簧的作用下,流通阀贴紧活塞,压缩腔的液体只能通过流通阀片的常通孔进入活塞的常通孔。与此同时,复原阀克服压紧弹簧的作用力,盖板与叠加阀片形成较大的缝隙而形成平面通道。油液通过流通阀、活塞常通孔、复原阀常通孔、平面通道和盖板常通孔进入复原腔。由于油液没有流经较小的叠加阀片缝隙,产生的阻尼力较小。因此,减振器压缩行程的阻尼力小于复原行程的阻尼力。叠加阀片缝隙的液流通道如图2所示。

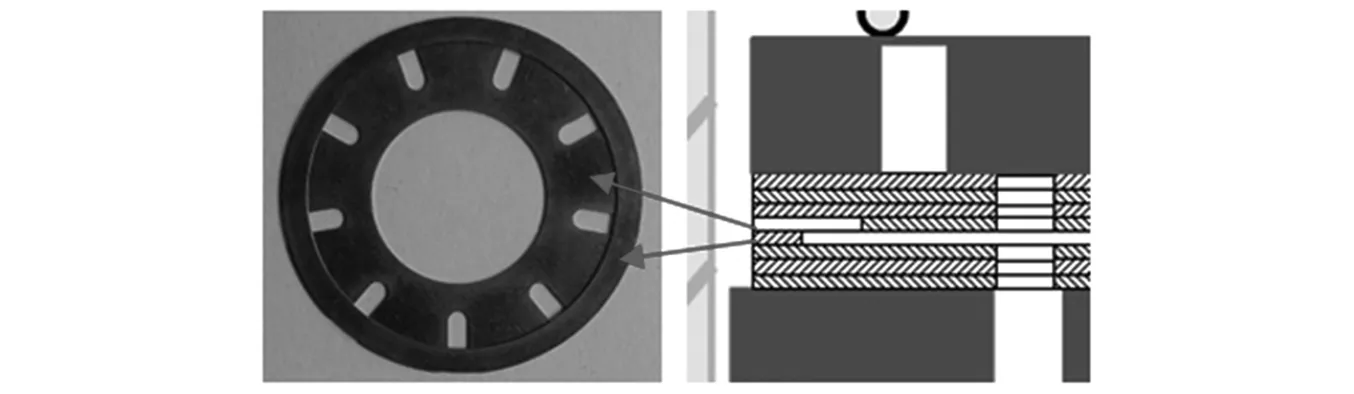
图2 叠加阀片缝隙Fig.2 Gap in the multiple valve plates

2 叠加阀片减振器数学建模

2.1 减振器物理模型

减振器物理模型用于描述阻尼力产生的机理,是车辆悬架建模的重要部分。根据黏性阻尼模型,阻尼力为阻尼系数和活塞速度的函数,表示为

F(v)=c(v)v

(1)

式中,c(v)为减振器的阻尼系数,是关于活塞速度的非线性函数。

减振器的阻尼系数反映了油液在活塞运动时流过小孔或狭缝时的阻力作用,与油液的黏度和流道特性有关。建立减振器物理模型的目的是为了通过压力模型和流量模型描述减振器产生阻尼力的机理。压力模型用微分方程来预测腔内压力,而流量模型用静力方程来计算油液在复原腔和压缩腔之间流动的压力变化[21]。阻尼力由复原腔和压缩腔的压力,以及摩擦力和缓冲力组成,表示为

F(v)=(Apt-Arod)Preb-AptPcom+Ffri+Fbum

(2)

式中:Apt和Arod分别为活塞和活塞杆面积;Preb和Pcom分别为复原腔和压缩腔的压力;Ffir为活塞与缸壁之间摩擦力;Fbum为储油腔压缩气体的反作用力。如果忽略气体温度变化,储油腔压缩气体的压力表示为

(3)

Vg=Vg0+Arodx

(4)

式中:Pg和Vg分别为气体压力和体积;Pg0和Vg0分别为气体的初始压力和体积;n为气体多变指数;x为活塞移动的位移。

复原腔通过复原阀和复原流通阀与压缩腔连接。复原腔的压力为

Preb=Pcom+ΔPp

(5)

式中, ΔPp为油液流经复原阀和复原流通阀后的压降。

当活塞速度较低时,复原腔与压缩腔的压差不够大,产生的压力无法克服垫片刚度而使之变形,因此油液只通过图2所示的缺口垫片节流孔流出。缺口垫片节流孔流量与压力降的关系为

(6)

式中:Q1为缺口垫片节流孔的流量;l,b和h分别为缺口的长、宽和高。

然后,油液从缺口垫片的节流孔进入活塞的6个节流孔。活塞节流孔流量和压降的关系为

(7)

式中:Q2为活塞节流孔的流量;Cq为流量系数;A2为节流孔面积;ρ为油液密度。

最后,油液经过流通阀进入压缩腔。由于流通阀弹簧的预紧力较小,因此流通阀所产生的压力降可忽略不计。

油液从复原腔进入压缩腔的第二个通道是活塞与缸壁之间的环形缝隙,其流量与压降的关系表示为

(8)

式中,d为活塞直径。

当复原腔与压缩腔的压差足够大时,所产生的压力能导致垫片变形。当复原腔压力大到足以克服垫片刚度,且活塞移动速度较高时,垫片产生变形而形成圆柱液流通道。油液除了从式(6)表示的缺口垫片节流孔流过,还可以从该圆柱液流通道流过。需要注意的是,流入圆柱液流通道的油液来自6个缺口垫片节流孔,压降同样由式(7)计算,流量定义为Q4。油液流经圆柱液流通道的流量与压降的关系为

(9)

式中:r为圆柱通道的半径;δ垫片变形量。

在保证精度的前提下,压缩阀可以简化为孔径固定的节流孔,流量与压降的关系为

(10)

复原流通阀和压缩流通阀的流量和压降的关系可简化为线性模型[22],表示为

Qci=KciΔPci

(11)

Qri=KriΔPri

(12)

式中,Kci和Kri分别为复原流通阀和压缩流通阀的流量梯度。

流入和流出减振器活塞的流量相等,因此存在

(13)

式中,Qr为复原阀的流量,且Qr=Qri。

对于减振器,还需满足

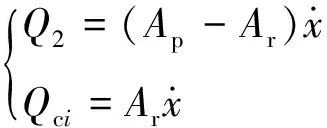
(14)

(15)

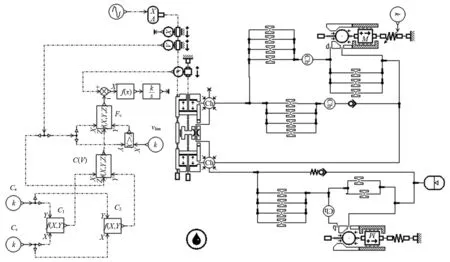
2.2 基于AMESim的减振器建模

在建立减振器物理模型时,首先根据式(14)和式(15)计算活塞节流孔、复原流通阀、压缩阀和压缩流通阀的流量,然后由式(13)计算出其他阀的流量,进而根据流量与压降的关系,如式(6)～式(12)计算各阀系的压降。当式(5)计算出复原腔和压缩腔的压力时,阻尼力最后由式(2)计算得到。由式(9)和式(10)可知,复原阀和压缩阀的垫片变形量需要在计算压降前确定。垫片变形量与垫片刚度直接相关,因此,如何确定垫片刚度是关键。另一方面,本研究的减振器复原阀由相同半径和厚度的垫片叠加而成,叠加垫片的整体刚度并不是每个垫片刚度的简单叠加。为此,本研究通过对叠加垫片进行有限元建模,分析得到其整体刚度。

图3(a)为垫片阀片的有限元模型。为了保证分析的准确性,将垫片轴向的网格尺寸定义为0.05 mm,确保每个垫片有限元模型在厚度方向上有四层网格。由于有限元网格较小,整个模型的网格数达到百万级,需要较长的后处理时间。考虑到叠加阀片的轴对称特点,可以在极半径上提取小部分网格来代替整个有限模型,如图3(b)所示。当在网格切向上进行适当约束时,所提取的小部分网格能代替整体有限模型。

叠加阀片有限元静力分析时,还需:①建立接触面,每个垫片之间的接触关系定义为触点,触点类型为滑动;②建立约束,除了在轴对称模型的切向进行约束外,在支承板和活塞接触处的施加零位移约束;③施加载荷,叠加阀片的载荷来自于上、下腔之间的压差,因此应施加分布载荷。

通过有限元模型的静力学分析,叠加阀片向上和向下变形的位移模型为

δu=0.224 7ΔP3

(16)

δl=0.080 5ΔP3

(17)

根据叠加阀片式减振器的工作原理和阻尼力产生机理,基于AMESim建立如图4所示的减振器模型。2.1节的减振器物理模型描述了阻尼力产生的机理,是利用AMESim建立减振器模型的思路,起指导作用。减振器的AMESim模型包括了减振器结构参数,便于后续的结构参数优化。为了保证复原流通阀和压缩流通阀能立即开启,虽然它们具有刚度和预紧力,但都较小,对复原和压缩行程的流动特性影响较小。因此,建模时将它们简化为止回阀。

图4 叠加阀片式减振器的AMESim模型Fig.4 AMESim model of the shock absorber with multiple valve plates

叠加阀片式减振器的节流阀由多片阀片叠加而成,其弯曲变形规律是减振器阻尼特性的关键。叠加阀片半径r处的弯曲变形量通过式(18)描述[23]

(18)

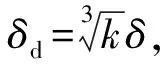
复原阀的常通孔模型为BH0011阻尼孔模型。缺口阀片的缺口流通面积为

Af=bh

(19)

式中:b为缺口宽度;h为阀片厚度。

等效流通半径为

(20)

式中,De为等效流通半径。

3 减振器物理模型精度校验

3.1 减振器阻尼特性试验

为获得减振器的阻尼特性曲线,以图5所示的方法安装减振器于专用的试验台架上,参照国家标准QC-T 545—1999《汽车筒式减振器台架试验方法》进行减振器速度特性试验。减振器阻尼特性试验的活塞最大速度分别取0.1 m/s,0.2 m/s,0.3 m/s、0.6 m/s,1.0 m/s和1.4 m/s多个工况。当减振器行程为S=0.1 m,即幅值为0.05 m时,通过式(21)可计算得到正弦激励信号的频率,如表1所示。

表1 活塞最高速度和正弦激励信号的频率对应关系

图5 建模减振器的阻尼特性试验Fig.5 Experimental damping characteristics of the modeled shock absorber

(21)

式中:v为减振器活塞最大速度;S为减振器行程;f为试验正弦激励信号的频率。

由于减振器试验台可以直接记录的数据是阻尼力与位移,减振器的示功特性图可以直接根据采集的数据绘制。但是,减振器的阻尼特性图需要活塞的运动速度,因此需要利用减振器试验台采集的离散位移数据进行数值微分,求出各点的速度。在计算活塞速度时,第一点的速度与最后一点的速度采用三点法计算,即

(22)

(23)

而中间各点的速度可以用相邻两点的位移来计算,即

(24)

式中:n为数据采样总数;v(1),v(n)和v(i)分别为第一点、最后一点和第i点的减振器活塞速度; Δt为数据采样时间间隔。

根据表1设定液压伺服系统产生正弦激励的频率,采集阻尼力和活塞速度信号,可得到如图6(a)所示的减振器不同工况下的示功图。采用多工况法合成的减振器阻尼特性如图6(b)所示。由于阻尼特性没有滞环现象,在车辆动力学仿真时是常用的减振器数学模型。

3.2 精度校验

以试验时施加的4种正弦激励频率和幅值为输入,通过对比分析减振器阻尼力检验AMESim模型的精度。在4种正弦激励下的减振器示功图如图7所示。图7中:实线为试验数据;虚线为仿真数据。由图7可知,减振器的AMESim模式输出的阻尼力与试验数据非常接近,说明AMEsim模型的精度较高,可用于后续的减振器结构参数优化设计。另外,从图7还可看出,激励频率越低,减振器的AMESim模型精度越高。这是因为当激振频率较高时,减振器横向刚度较低而发生剧烈的左右晃动,导致试验数据重复性较低。

图7 减振器物理模型精度检验Fig.7 Accuracy verification of the physical model of the shock absorber

4 减振器结构参数优化

4.1 最优阻尼特性曲线的确定

图6(b)所示的减振器非线性阻尼特性曲线可分解为三部分:第一部分为压缩行程的曲线(AB段);第二部分为复原阀开启前的复原行程曲线(BC段);第三部分为复原阀开启后的复原行程曲线(CD段)。描述减振器非线性阻尼特性的Besinger模型表示为[24]

(25)

式中:v为活塞速度;vlim为复原阀开启时的活塞速度;Ce为复原阀开启前阻尼系数;Cb为复原阀开启后的阻尼系数;C(v)为非线性阻尼系数,表示为

(26)

式中,α为阻尼转换参数;c1=0.5(Ce-Cc);c2=0.5(Ce+Cc);Cc为压缩行程的阻尼系数。

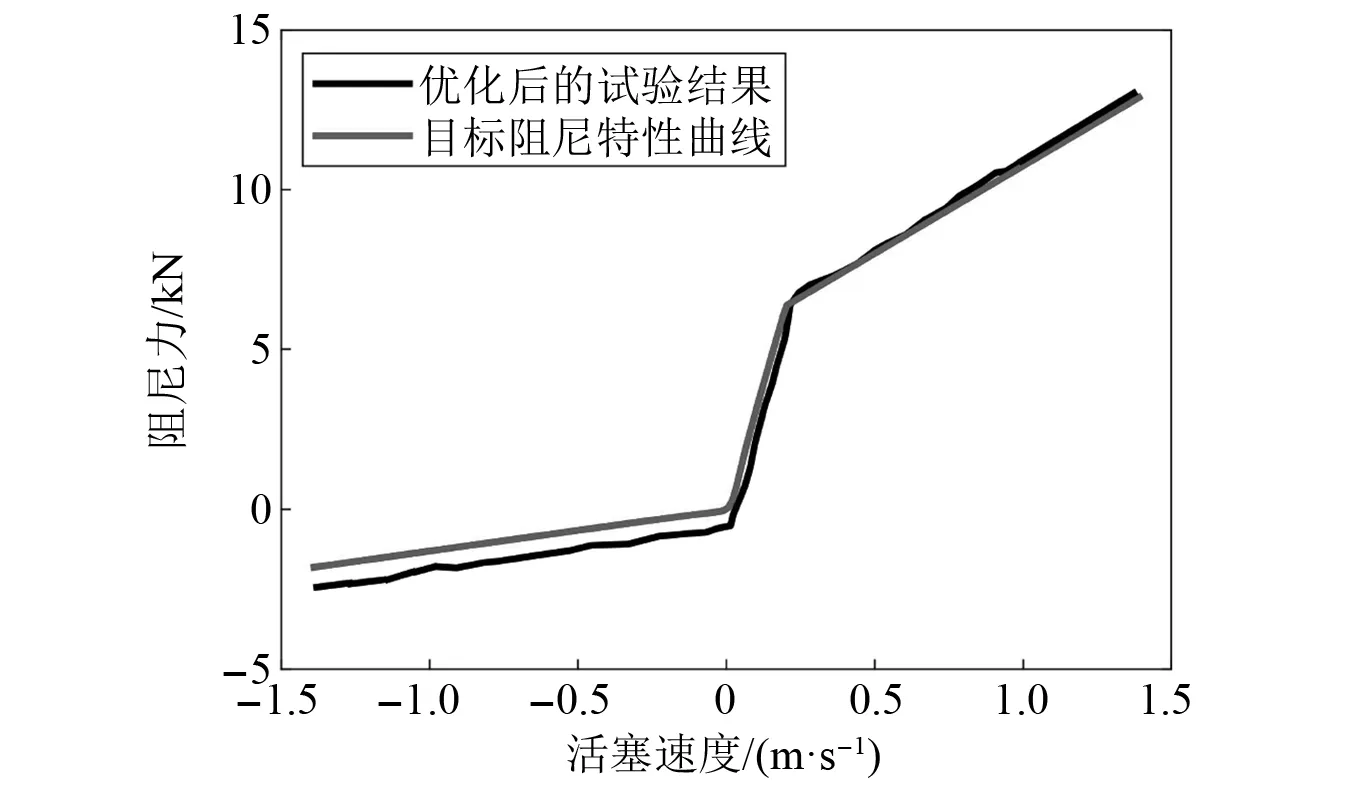
在式(25)和式(26)所表示的减振器非线性阻尼特性曲线中,待定参数为Cc,Ce,Cb,α和vlim5个参数。非线性阻尼系数C(v)实际上是压缩行程和复原行程前期的阻尼系数组合,切换位置由阻尼转换参数α决定。因此,当v

图8 减振器目标非线性阻尼特性曲线Fig.8 Target nonlinear damping characteristic curve of the shock absorber

利用ADAMS/Insight模块基于平顺性对减振器非线性阻尼特性模型的Cc,Ce,Cb,α和vlim5个参数进行灵敏度分析。分析过程中,上述参数分别以名义值变化±50%。客车满载工况下行驶速度为70 km/h,路面为B级路面。5个参数对驾驶员座椅处垂直加速度的贡献率分别为:16.42%,38.49%,8.16%,27.41%和9.52%。因此,选择压缩行程的阻尼系数Cc、复原阀开启前阻尼系数Ce和阻尼转换参数α3个参数为设计变量。本文采样遗传算法进行参数优化,参数如表2所示。为保证车辆的操纵稳定性,本研究选择稳态回转试验的综合评价指标为约束函数,如

表2 遗传算法参数Tab.2 Genetic algorithm parameters

(27)

3个子评价指标分别为

(28)

(29)

(30)

上述3个子指标的定义、参数意义和取值参考国家标准GB/T 6323.6—1994《汽车操纵稳定性试验方法-稳态回转试验》确定。目标函数定义为驾驶员座椅处和同侧最后一排乘客座椅处的加速度综合值之和,其中加速度综合值表示为

(31)

式中,axw,ayw和azw分别为座椅处X,Y和Z3个方向上的加权有效值。

3个设计变量的设计空间定义为原值的50%～150%。建立的优化模型为

(32)

通过MATLAB与ADAMS联合仿真实现对减振器非线性阻尼特性模型3个参数的优化。利用MATLAB脚本文件编写基于遗传算法的优化模型,MATLAB/Simulink建立减振器非线性阻尼特性模型,并以为减振器的阻尼力为输出变量,驾驶员座椅处和同侧最后一排乘客座椅处X,Y和Z3个方向上的加速度、横摆角速度、侧倾角速度等车辆状态为输入变量,实现与ADAMS/Car车辆动力学模型的信息交互。通过MATLAB脚本文件调用Simulink模型,进而调用车辆动力学模型计算车辆状态信号,完成减振器非线性阻尼特性模型的参数优化,获得减振器的最优特性曲线。

优化后的减振器非线性阻尼特性曲线如图8(b)所示,阻尼特性模型的3个参数为:Cc=2.08 kN/(m/s),Ce=35.95 kN/(m/s),α=0.09 m/s。驾驶员座椅处的总加权有效值由原来的0.432 8 m/s2降低到0.387 9 m/s2,降低幅度为10.37%。同侧最后一排乘客座椅处的加速度由原来的0.503 6 m/s2降低到0.442 1 m/s2,降低幅度为12.21%。另外,稳态回转试验的综合评价指标为88.7,客车的操纵稳定性仍表现优秀。

4.2 减振器结构参数优化与性能检验

由减振器非线性阻尼特性模型参数对客车平顺性的灵敏度分析结果可知,压缩行程的阻尼系数Cc、复原阀开启前阻尼系数Ce和阻尼转换参数α3个参数对驾驶员座椅处的垂直加速度贡献度较大。根据阻尼力产生机理,本研究选择复原阀刚度、复原阀片压缩量、复原阀常通孔等效孔径和压缩阀刚度4个参数为设计变量,开展减振器结构参数优化。

以前悬架减振器的最优阻尼特性曲线为目标曲线,利用AMESim软件中自带有优化功能,采用遗传算法对减振器的结构参数进行优化设计。优化模型如图9所示。其中,减振器实际输出阻尼力与目标曲线之间误差的平方和最小为优化目标。优化结果为:复原阀片刚度为330 N/mm,复原阀片压缩量为0.72 mm,复原阀常通孔等效孔径分别为1.30 mm,压缩阀片刚度为75 N/mm。

图9 减振器结构参数的优化模型Fig.9 Optimization model of shock absorber parameters

优化结果是复原阀常通阻尼孔的等效直径,还需根据优化结果进行阀系结构的尺寸设计。复原阀常通阻尼孔的等效直径为1.30 mm,单个孔的流通面积为1.33 mm2,修改阀片的宽度为3 mm。利用叠加阀片的特点,根据阀片数量与刚度的关系,确定4片叠加阀片的刚度为360 N/mm,接近330 N/mm,因此复原阀片数减小1片为4片。最后通过调整垫片的厚度获得复原阀的压缩量。压缩阀片减少2片为5片,缺口阀片尺寸不变。

确定减振器阀系的尺寸后加工为减振器原型,采用原试验设备和方法进行阻尼特性试验,如图10所示。减振器原型的速度阻尼特性曲线与目标阻尼特性曲线对比如图11所示。由图可知,优化后的减振器结构参数能较准确地实现目标阻尼特性。其中复原行程的最大阻尼力相对误差为8.11%,压缩行程的最大阻尼力相对误差为24.30%。

图10 减振器原型的阻尼特性试验Fig.10 Test damping characteristics of the shock absorber prototype

图11 优化前后的减振器阻尼特性对比Fig.11 Comparison of damper damping characteristics before and after optimization

需要说明的是,本研究进行了两次优化。第一次优化是利用MATLAB与ADAMS联合仿真对减振器非线性阻尼特性模型的3个参数进行优化,获得减振器的目标特性曲线。第二次优化利用AMESim软件自带有优化功能,对减振器的4个结构参数进行优化,优化目标是实现减振器的目标特性曲线。

为验证减振器结构参数的优化效果,开展了客车平顺性和操纵稳定性的实车试验验证(如图12(a)所示)。信号采集系统为北京星网宇达科技开发有限公司的XW-ADU5630姿态方位组合导航系统(如图12(b)所示)。该系统不仅能采集加速度信号,还能通过GPS信号计算车速、横摆角、侧倾角等车辆状态。平顺性试验中信号采集系统安装在驾驶员座椅处。操纵稳定性试验中信号采集系统安装在客车质心处,GPS天线安装在车窗的玻璃上(如图12(c)所示)。信号采集系统的采样频率为100 Hz,两个试验都在客车满载条件下进行。平顺性试验时车速为45 km/h,安装优化前后减振器的两辆客车行驶同一段道路。由图12(d)可知,减振器优化后,客车驾驶员座椅处垂直方向的加速度明显小于减振器优化前。减振器优化前的总加权加速度有效值为0.442 1 m/s2,减振器优化后的总加权加速度有效值为0.361 8 m/s2,降低幅度为18.16%,说明优化的减振器结构参数能有效改善客车的平顺性。

图12 试验验证与结果对比Fig.12 Experimental verification and comparison results

操纵稳定性试验同样参考国家标准GB/T 6323.6—1994《汽车操纵稳定性试验方法-稳态回转试验》进行。设定稳态回转圆周半径为20 m;保持方向盘转角不动,在指定的时间内缓慢均加速(纵向加速度不大于0.25 m/s2),直到车辆出现不稳定状态,驾驶员感觉无法安全操控车辆为止。如图12(e)所示,减振器优化后能让客车行驶速度达到34 km/h,相对减振器优化前的28 km/h,提高了21.42%。在此过程中,侧向加速度和横摆角速度对比分别如图12(f)和图12(g)所示。两个车辆状态并未出现急剧增加,车辆保持较好的操纵稳定性。根据式(27)计算得到客车稳态回转试验的综合评分值为89.6,进一步证明客车的操纵稳定性得到了保证。