基于能量辐射传递法的功能梯度板高频振动响应分析
2023-12-01许爱林代成浩陈海波
许爱林, 代成浩, 陈海波
(1. 中国科学技术大学 中国科学院材料力学行为与设计重点实验室,合肥 230226;2. 中国科学技术大学 近代力学系,合肥 230026)
在航空航天等工程应用中,结构在复杂恶劣的环境下容易出现高频载荷的作用。若设计不当,会成为引发结构的高量级噪声、疲劳失效甚至强度破坏的重要因素[1]。因此,研究结构的高频振动问题对避免结构损伤失效和更好地减振降噪非常重要。20世纪80年代,Koizumi[2]首先提出了功能梯度材料(functionally graded materials,FGM)的概念。功能梯度材料是一种特别的复合材料,通常由两种或更多材料成分组成,在微观上不均匀混合分布,其材料特性在选定的方向上平缓渐变[3]。复合材料板是工业领域最广泛应用的结构之一。在传统的复合材料层压板中,高局部层间应力引起的层间分离会导致结构和功能失效。功能梯度板材料成分在空间上连续变化,可有效消除层间应力,因此被广泛应用于涡轮叶片、热障涂层、火箭喷嘴等结构[4]。近年来,伴随着飞行器速度提高和轻量化的需求,功能梯度结构的运用越来越多,因此研究功能梯度板的高频振动响应对提高结构性能有着重要的意义。
传统有限元法(finite element method,FEM)和边界元法(boundary element method,BEM)等算法计算高频响应有计算成本高、非确定性因素敏感等局限[5]。为了避免这些问题,学者们提出了若干能量方法。其中统计能量分析 (statistical energy analysis,SEA)法[6-7]首先被提出并已广泛应用于计算各类工程问题的平均能量响应,该方法以每个子系统内的平均振动能量为主变量,因此无法预测子系统内的能量分布。为了解决这个问题,相关学者提出了振动传导法(vibrational conductivity approach,VCA)[8],该方法基于混响场假设,由傅里叶热传导定律类比得到能量控制方程,结合边界条件求解此能量控制方程的方法被称为功率流分析(power flow analysis,PFA)[9],而用有限元求解该方程的方法被称为能量有限元法(energy finite element method,EFEM)[10]。VCA假设振动场由平面波叠加而成,由于平面波只在一维系统中严格成立,而在二维和三维系统中,振动则分别以柱面波和球面波的形式传播,因此该方法预测二维、三维系统能量并不准确。于是Le Bot[11-12]提出了能量辐射传递法(radiative energy transfer method,RETM),该方法基于几何声学,类比热辐射传递,不仅可以给出系统内的能量分布而且对二维、三维系统求解精度高于VCA[13]。周红卫[14]采用RETM求解了薄板和梁的高频振动的能量响应,并与 EFEM 进行了对比。钟强等[15-16]将RETM应用到各向异性介质模型中,验证了在二维结构中RETM结果准确性高于VCA。
目前,学者们已基于不同的理论和数值方法对功能梯度结构动力学特性进行了研究。Yang等[17]研究了热环境下材料分布和温度场等因素对功能梯度板的振动和声辐射特性的影响。Chen等[18]建立了功能梯度夹芯板的声振耦合动力学方程,对功能梯度板的隔振特性进行了研究。Loja等[19]利用Rayleigh-Ritz法和Bolotin法分别研究了功能梯度板自由振动和动力失稳问题,并分析了体积分数分布的影响。Papkov等[20]用动力刚度法研究了正交各向异性Mindlin板的自由振动特性。在高频能量计算方法方面,张玲等[21]对功能梯度板进行了功率流分析。Liu等[22]建立了功能梯度梁的振动能量流模型,分析了材料梯度因子对能量响应的影响。
目前,一阶剪切变形理论和RETM还未被用于求解功能梯度板的高频振动响应。本文根据功能梯度板的力学性能,推导了振动控制方程,建立了一阶剪切理论框架下功能梯度板的高频振动能量辐射传递模型。与模态叠加法和PFA计算结果进行了对比,验证了RETM模型的正确性以及在计算不同物理参数下功能梯度板高频振动响应的准确性。最后讨论了激励频率、材料梯度因子和结构阻尼对能量响应的影响。本文工作是功能梯度板高频振动分析方法研究的一个新进展,为结构高频振动能量空间分布的高精度计算提供了新手段。
1 功能梯度板振动模型
1.1 功能梯度板材料特性
考虑一长宽高为a×b×h的功能梯度板,建立如图1所示的笛卡尔坐标系,板由两种材料组成,材料在z方向连续变化,下面假设材料特性P(z)按照幂函数形式分布[23]
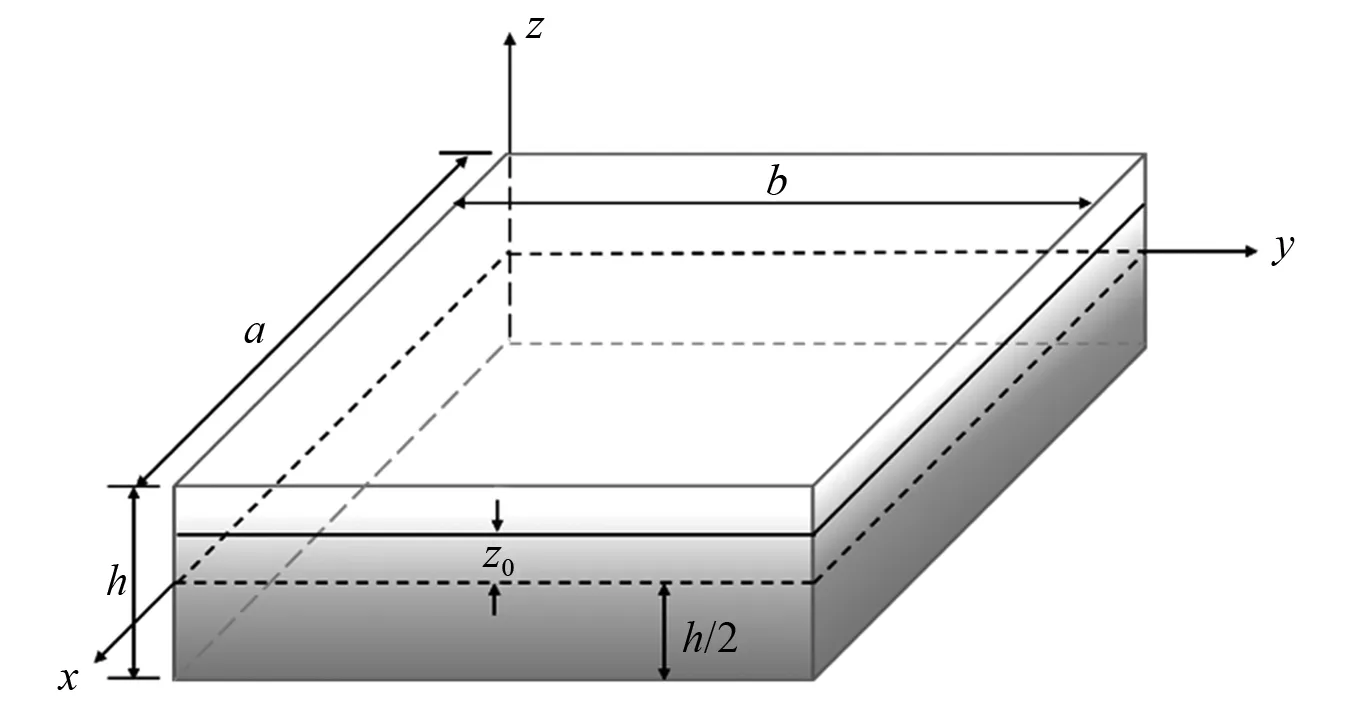
图1 功能梯度板模型Fig.1 Functionally graded plate model
(1)
式中:Ptm和Pbm分别为顶层和底层材料特性;P(z)为弹性模量、质量密度以及阻尼损耗因子等材料参数。
1.2 功能梯度板振动控制方程
不同于均匀各向同性板,功能梯度板的材料组成和特性关于几何中面并不对称,在该基准面上存在平面内拉伸或压缩,因此,通过合理地选择没有面内位移的平面作为参考平面,可以消除面内拉伸和弯曲的耦合,该平面被称为中性面。功能梯度板的中性面到几何中面的位置表达式为[24]
(2)
式中,E(z)和μ(z)分别为弹性模量和泊松比。
一阶剪切变形理论(first-order shear deformation theory,FSDT)考虑了转动惯量和剪切变形的影响,基于FSDT对功能梯度板振动控制方程进行推导,板内任意一点位移可以表示为
ux(x,y,z,t)=(z-z0)φx(x,y,t),
uy(x,y,z,t)=(z-z0)φy(x,y,t),
uz(x,y,z,t)=w(x,y,t)
(3)
式中:ux,uy,uz分别为x,y,z方向的位移;φx和φy分别为沿x轴和y轴的旋转角度;w为中性面的位移。
与位移相关的应变分量可表示为
(4)
功能梯度板中的应力应变关系可表示为
(5)
式中,Qij为模量系数。
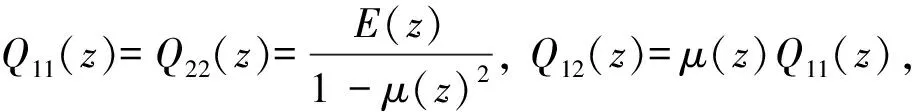
(6)
式中,κ为剪切修正因子。在一阶剪切功能梯度板中,势能和动能可以表示为
(7)
(8)
总外力做功为
(9)
式中: 外力f(x,y,t)=Feiωtδ(x-xs)δ(y-ys); (Aij,Dij)分别为面内拉伸刚度矩阵和弯曲刚度矩阵; (I0,I2)为质量的惯性矩。
(10)
建立拉格朗日算子δL=δT-δU+δW,根据哈密顿原理,得到一阶剪切功能梯度板横向振动控制方程

(11)
1.3 板中的波传播
由于振动控制方程中横向位移与转角耦合,为了得到面外运动的通解,需要引入亥姆霍兹分解定理进行解耦[25],定义位移势函数φ和ψ
(12)
将式(12)代入控制方程式(11)中,得到解耦后的控制方程
(13)
(14)
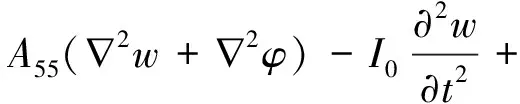
(15)
考虑板上没有外力时的自由振动问题。将行波解ψ=A1e-i(k1xx+k1yy)+iωt代入式(14)中,得到位移势函数ψ的波数k1和频率关系的频散方程
(16)
得到位移势函数ψ的波数k1为
(17)
(18)
将w=A2e-i(kxx+kyy)+iωt和φ=A3e-i(kxx+kyy)+iωt的行波解代入式(13)和式(15)的齐次形式,得到频散方程
D11A55k4-(D11I0ω2+A55I2ω2)k2-
A55I0ω2+I0I2ω4=0
(19)
方程的四个根为
(20)
(21)

位移势函数φ和横向位移w的临界频率与位移势函数的临界频率相同,因此在一阶剪切板横向振动中只存在一个临界频率ωc,该临界频率由功能梯度板的材料属性与厚度决定。临界频率随着弹性模量增大而增大,随着密度增大而减小,并与板厚度成反比。
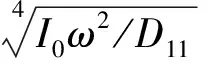
当ω<ωc,与弯曲效应相关的项占主导地位。只有波数k2是纯实数,对应着板中只存在一种传播波并由弯曲变形主导,k1和k3对应倏逝波;随着频率增大,剪切变形和转动惯量对板中波传播的影响变大。当ω>ωc,波数中与剪切变形和转动惯量效应相关的大于与弯曲效应相关的项。k1和k3仅在剪切变形占主导地位时传播,此时板中存在k1,k2,k3均为实数,对应为三种传播波。
位移势函数φ和横向位移w的通解可以用各个行波分量叠加表示为
(22)
式中,j为波的类型。波分量的群速度可定义为

(23)
1.4 能量密度与功率流强度
功能梯度板中的能量密度包含动能密度和势能密度,即W=Wk+Wp。
动能密度由横向运动的动能和旋转动能组成,表达式为
(24)
势能密度由弯曲变形和剪切变形的势能组成,表达式为
(25)
功率流强度由剪力和力矩传递,可表示为I=Ixex+Iyey
(26)
式中,剪切力Qxz和Qyz、弯矩Mx和My以及扭矩Mxy和Myx可表示为
(27)
时间平均的能量密度和功率流强度可以分解为每个传播波的叠加,将ψ,φ和w的通解代入式(24)、式(25)和式(26),得到功能梯度板能量密度和功率流强度表达式

(28)

(29)

能量速度为
(30)
可以推出能量速度与波群速度相等,因此,对于基于一阶剪切变形理论的功能梯度板,功率流强度与能量密度成正比,比例关系为群速度。
1.5 板在点激励下的远场响应和输入功率
对板的控制方程式(13)和式(15)进行傅里叶变换,得到波数空间下的横向振动响应幅值
w∞(k,t)=
(31)
并用极坐标表示其解,根据贝塞尔函数性质和留数定理[26]可得横向位移的远场解

(32)
激励点(r=0)处的横向振动速度为
(33)
输入功率通过无限场导纳Y∞估计
(34)
2 功能梯度板的能量辐射传递模型
在稳态条件下,二维结构能量平衡方程为
∇I+Pdiss=Pin
(35)
在PFA中,基本假设为振动场由平面波控制,功率流强度与能量密度的梯度成正比

(36)
得到功能梯度板振动传导法的能量控制方程[27]
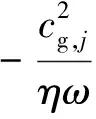
(37)
在RETM中,假设功率流强度I直接与能量密度W成正比I=ceW,比例系数为能量速度向量ce。前一节已证明能量速度与群速度相等,因此I=cgW。这样,基于RETM的功能梯度板能量平衡方程
∇·(cgjWj)+mjcgjWj=Pin,jδ(x-xs,y-ys)
(38)
式中,mj=ηω/cgj为能量衰减系数。求解式(38)可以获得第j类波的能量密度Wj和功率流强度Ij的自由场解
(39)
式中:r为距离;u(θ)为方向向量。对于二维结构,板上任意接受点M的能量由点源S对点M产生的直接场与边界虚源产生的反射场叠加而成。
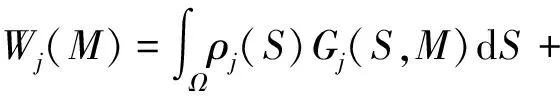
(40)
(41)
式中,r=|S-M|或r=|P-M|分别为点源S或虚源P到接收点M的距离。由横向位移的远场解表达式(32)可知,W(r)∝e-2Im(kj)r/r,对比核函数,得到能量衰减系数的等效表达式,得到mj=2Im(kj)。
板边界Pk处虚源的功率流平衡方程可以表示为
(42)
在数值模拟中,将板边界划分为n个单元,单元长度为Lk。离散的二维板结构能量辐射模型如图2所示,式(42)可写为
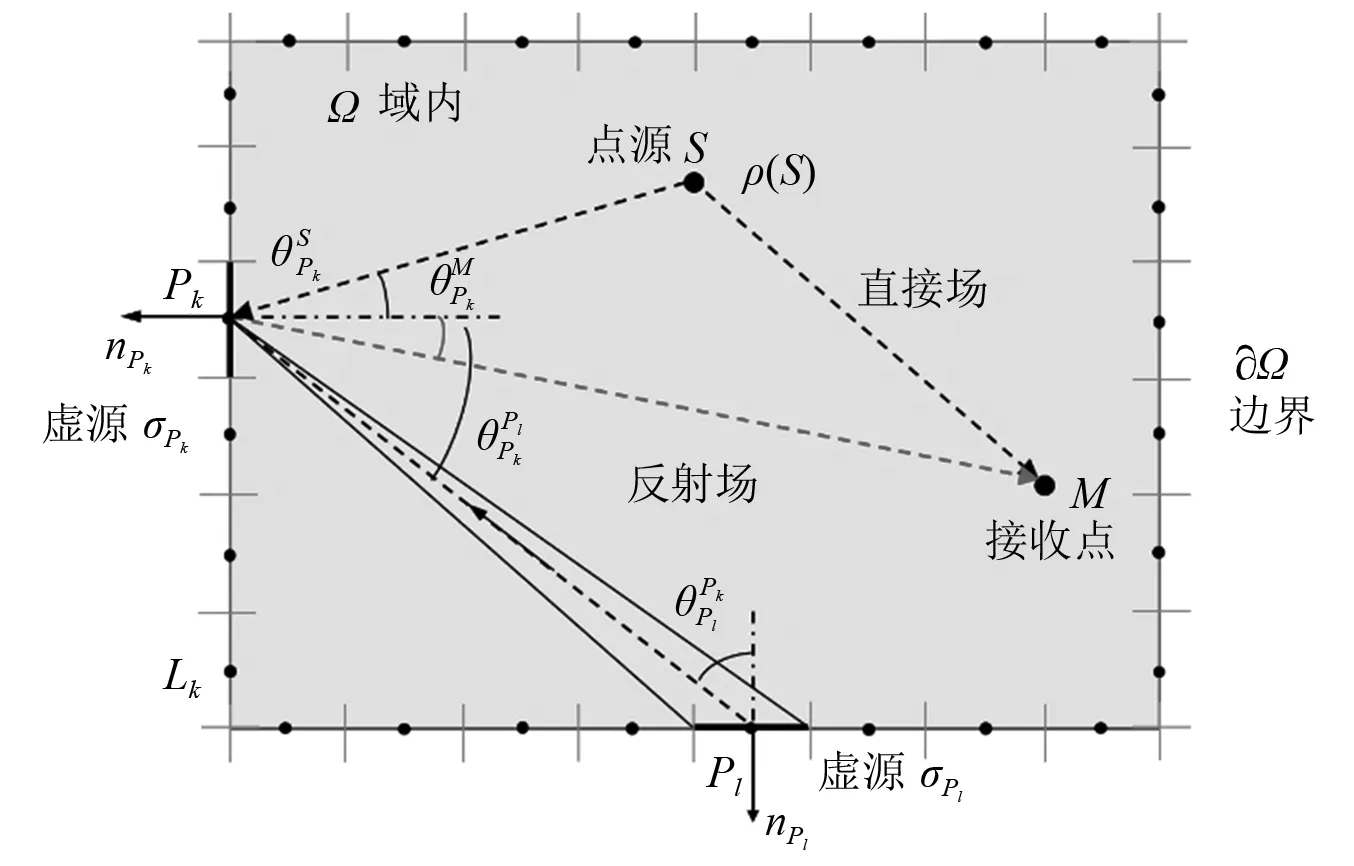
图2 离散边界的二维结构能量辐射传递模型Fig.2 Radiative energy transfer model of a two-dimensional structure with discrete boundaries
(43)
临界频率以下,板中只有一种传播波,能量场为波场2控制的直接场与反射场能量的叠加;临界频率以上,能量场为三种波场控制的实源产生的直接场与虚源辐射能量的叠加。通过离散边界,板内接收点的能量密度和功率流强度表示为
W(M)=
(44)
I(M)=
(45)
3 数值算例和讨论
建立一个材料由金属和陶瓷组成的功能梯度板模型,顶层材料为Si3N4,底层材料为SUS304,表1为所用的材料属性。长宽厚为1 m×1 m×0.01 m,板中间位置(0.5,0.5)施加幅值为1的横向谐波点激励Feiωt。

表1 Si3N4和SUS304的材料属性Tab.1 Material properties of Si3N4 and SUS304
首先分析功能梯度板的波传播特性。图3给出了分别基于FSDT和CPT下,功能梯度板各个传播波分量的波数和波速随频率的变化曲线,并将两种理论模型得到的波数和波速进行了对比。从图3中可以看出,在频率较低的情况下,两种理论得到的波数和波速是一致的,群速度cg为相速度cp的2倍,此时弯曲变形占主导地位;当频率达到20 kHz左右时,FSDT的波数大于CPT的,而FSDT的波速小于CPT的,群速度cg与相速度cp逐渐相等;随着频率增大,剪切变形和转动惯量对板中波传播的影响变大。该模型的临界频率为fc=214 kHz,当频率低于临界频率时,一阶剪切功能梯度板中只有一个弯曲主导波,高于临界频率时,第二、第三个传播波开始出现,称为面外剪切波和剪切主导波,当频率高于1 000 kHz时,其群速度和相速度随频率增大逐渐趋于一致。

图3 功能梯度板波数与波速随频率变化Fig.3 Variation of wave number and wave velocity of functionally graded plate with frequency
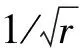
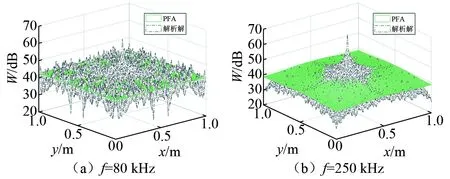
图5 不同频率下PFA解与解析解对比,η=0.01 (fc=214 kHz)Fig.5 Comparison of energy results by VCA and Analytic solution at different frequencies η=0.01 (fc=214 kHz)

图6 不同厚度下功能梯度板能量变化,η=0.01, f=250 kHzFig.6 Energy density of functionally graded plate under different thicknesses, η=0.01, f=250 kHz
从图5中可以观察到,阻尼相等的情况下,当f=80 kHz,波在传播过程中的能量衰减速度较慢,直接场与反射场的干涉现象明显。随着频率增大,板中传播波波数增加,波传播的周期增多。当f=250 kHz,能量衰减速度变快,自由场主导范围增加,衰减能级跨度增大,边界附近振荡幅度减小。
一阶剪切变形理论考虑了板的剪切变形与转动惯量的影响,在高频振动或厚板问题分析中,它们对波传播的影响非常大。对于长宽为1 m,厚度分别为0.001 m,0.005 m,0.010 m,0.050 m的功能梯度板模型,在激励频率250 kHz作用下,沿板中心线x=0.5 m截取的能量密度如图 6所示,对比了模态叠加法、RETM和PFA三种方法的解。在不同厚度下,RETM解与解析解均能吻合得非常好。当波在不同厚度的板中传播,随着板厚度的增大,临界频率fc减小,且与成正比。当厚度较小时,f
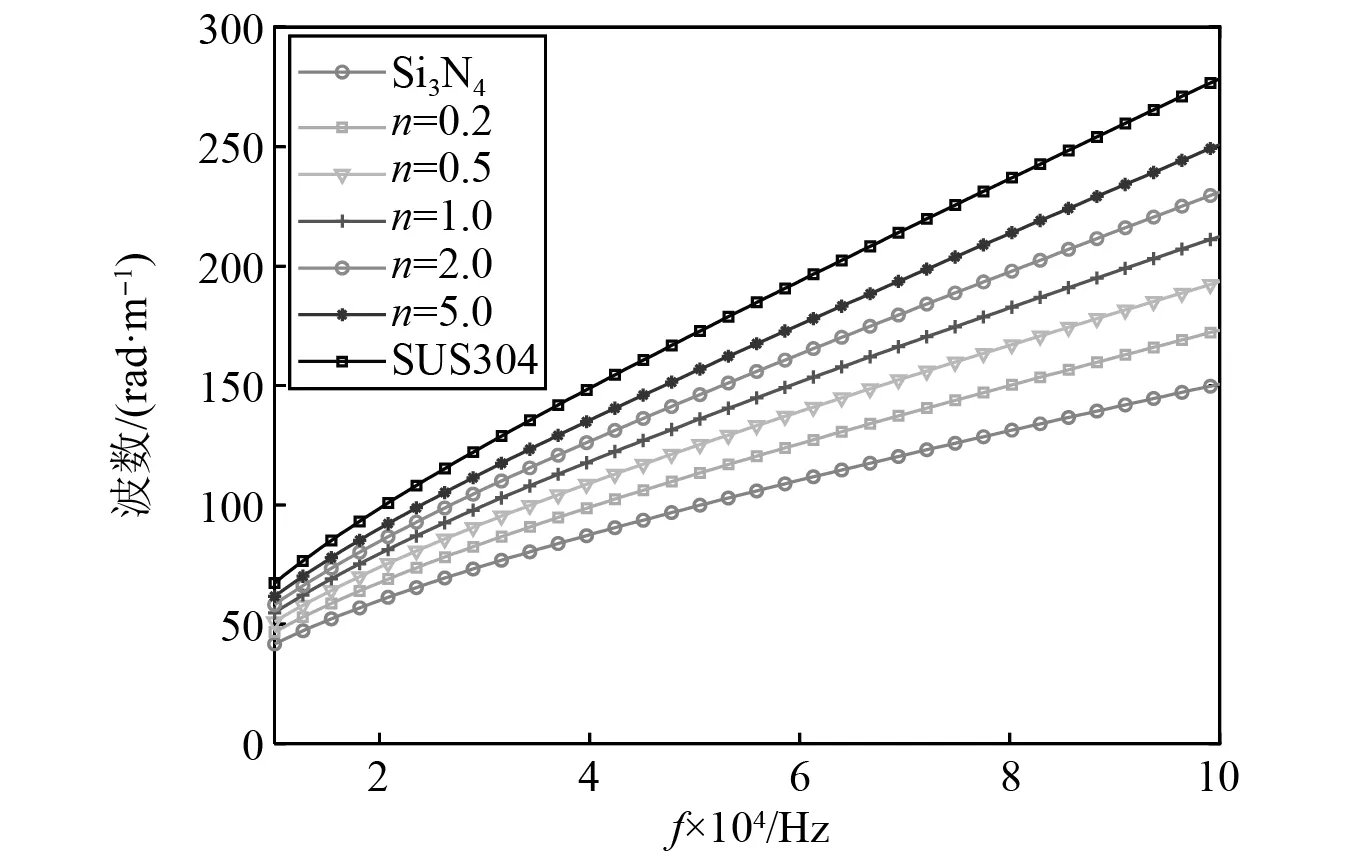
图7 不同n的功能梯度板波数与频率变化关系Fig.7 Variation of wave number with frequency of functionally graded plate with different n
图8给出了不同n的功能梯度板RETM能量变化。由于n增大不锈钢趋于主导地位,波数增大,导致波在板内传播所经历的衰减周期数增加。因此可以由图8观察到,阻尼和频率一定时,n越大,能量密度衰减速度越快,同时激励点处的能量密度增大,导致不同n的能量密度曲线之间有交汇。

图8 不同n下功能梯度板的RETM能量变化Fig.8 Energy density levels of functionally graded plate of RETM for various n
图9为不同材料梯度因子下,RETM解与解析解的对比。在这个算例中,将氮化硅的结构阻尼系数设为0.02,不锈钢的结构阻尼系数设为0.08,阻尼同样以幂函数形式渐变。对于不同的n,RETM解与解析解均能很好的吻合。n增大,结构的阻尼系数增大,能量损耗变大,边界附近的能量振荡幅度变小。

图9 不同n下功能梯度板能量变化RETM解与解析解 对比, ηt=0.02, ηb=0.08, f=80 kHzFig.9 Comparison of energy density of functionally graded plate by RETM solution and analytic solution for various, ηt=0.02, ηb=0.08, f=80 kHz
图10对比了不同阻尼下功能梯度板的能量密度分布。当频率一定时,阻尼较小,射线到达边界时仍携带较高的能量,经边界反射后,反射射线传播一定距离后才被吸收,板中从边界开始一定范围内的能量都由反射射线主导。相反,阻尼较大,衰减速度较快,反射波能量较小,与入射波干涉的范围有限,边界处振动幅度较小。

图10 不同阻尼下功能梯度板的能量密度f=100 kHzFig.10 Distribution of energy density in the FGM plate for various damping loss factors f=100 kHz
图11中对比了不同阻尼和频率下功能梯度板的功率流流场和等能量曲线。由于RETM忽略波和波之间的相互干涉,能量流线为平滑的曲线,从激励点开始以近似直线发射状传播,到达边界处被阻挡而弯曲。由图11(a)和图11(b)可看出,当频率一定,图11(a)的阻尼较大,能量等势线较为密集,梯度明显;图11(b)的阻尼较小,能量等势线稀疏,相邻等势线距离较远。对比图11(b)和图11(c),当阻尼一定,激励频率分别在临界频率以下和临界频率以上,发现频率越大,能量衰减因子越大,因此图11(c)比图11(b)从激励点到边界处能量跨度范围更大,等能量曲线更密集。

图11 不同阻尼、频率下功能梯度板的能量流场Fig.11 Energy flow fields in the FGM plate for various damping loss factors
在板中取坐标为(0.65 m,0.65 m)、(0.75 m,0.75 m)和(0.85 m,0.85 m)的三个位置,其能量响应水平随频率变化如图12所示。对于接受点的局部能量响应,RETM解与解析解整体变化趋势吻合较好。对于固定的位置,高频段反射波携带的能量耗散更快。越靠近边界处,反射场越占主导,当频率超过40 kHz,(0.65 m,0.65 m)处基本上只有入射波,反射波无法到达;点(0.85 m,0.85 m)较其他位置的局部能量仍有明显的振荡。
4 结 论
本文以功能梯度板为研究对象,基于一阶剪切变形理论,推导了功能梯度板的振动控制方程,得到了频散方程,分析其波传播特性。建立了激励频率分别小于和大于临界频率情况下功能梯度板的能量传递模型。数值算例中,将模态叠加法作为解析解,RETM和PFA分别与之对比,验证了能量传递模型的准确性。对比了不同厚度下,基于FSDT和CPT功能梯度板的能量响应水平。对功能梯度因子n、结构阻尼因子和激励频率的影响进行了参数敏感性对比分析,以研究功能梯度板的能量响应特性。得到了以下结论:
(1) 一阶剪切板横向振动中存在临界频率ωc。当ω<ωc,板中存在一种传播波,两种倏逝波;能量响应由该传播波控制;当ω>ωc,板中的倏逝波转变为传播波,能量响应由三种传播波控制。不同物理参数下,能量传递模型与解析解均能吻合较好。
(2) 当板厚度较小时,临界频率较大,剪切变形和转动惯量的影响与弯曲变形相比较小,FDST与CPT的能量密度差别不大;随着板厚度增大,剪切变形和转动惯量的影响增大,FSDT下的能量水平明显高于CPT,CPT对高频厚板模型不再适用。
(3) 随着n增大,功能梯度板中陶瓷材料占比减小,金属材料占比增大,板的韧性增加,波数变大,波在板内传播所经历的衰减周期数增加,衰减速度变快,能量衰减跨越能级越大。
(4) 频率和阻尼较小时,直接场在能量场中占主导地位,频率和阻尼的增加会导致波在板中传播时携带的能量被快速吸收,衰减幅度增加,振动幅度变小。
