由一道题谈解答三角形最值问题的路径
2023-11-30谢宏雷
谢宏雷


三角形最值问题经常出现在各类试题中,通常要求求三角形的某条边长、某个角、面积、周长的最值.三角形最值问题侧重于考查三角函数的定义、正余弦定理、勾股定理、三角形性质的应用.下面结合一道例题,谈一谈解答三角形最值问题的两个路径.
本题看似较为简单,其实有些复杂.由于无法确定D、E的位置以及DE的长度,所以我们很难确定∠ACB的大小.经过研究,笔者发现可通过构造三角形的外接圆,利用三角函数的有界性来求解.
一、构造三角形的外接圆
三角形的外接圆的圆心,即外心,是三角形三条边的垂直平分线的交点.外心到三角形的三个顶点的距离相等.在解答三角形最值问题时,可根据题意构造三角形的外接圆,利用外心的性质和圆的性质来确定三角形边、角的最值.对于本题,我们由“线段AC的垂直平分线分别交AB,AC于点D,E”,可联想到三角形的外接圆,于是构造三角形的外接圓,通过研究外接圆的性质,确定∠ACB的最大值.
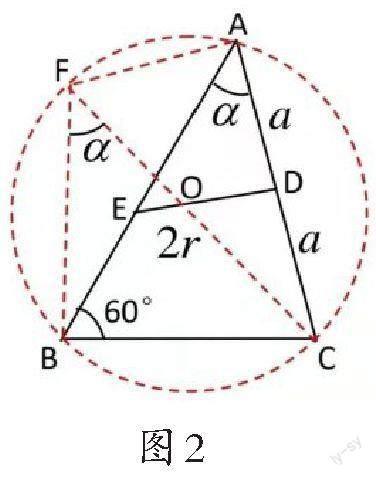
如图2,作△ABC的外接圆,设其圆心为O,连接CO,并延长CO到F点,使其与圆交于F点,连接AF,BF,设AD=DC=a,圆O的半径为r,∠BAC=α.
因为∠ABC=60°,
所以∠ACB=180°-60°-∠BAC=120°-α,
在Rt△BCF中,∠BFC=∠BAC=α,∠CBF=90°,
所以BC=CF·sinα,即4=2rsinα②.
在△ABC中,由正弦定理得AC=2rsin60°,
即2a=2rsin60°③.
由①②③得a=45°,所以∠ACB的最大值为75°.
在构造出三角形的外接圆后,通常既要灵活运用圆的性质,如同弧所对的圆周角相等,直径所对的圆周角为直角,弦心距垂直于弦等性质来确定三角形边、角的最值,还要用正余弦定理、勾股定理来建立边角的关系式.
二、利用三角函数的性质
在解答三角形最值问题时,我们往往要先根据题意设出三角形中未知的角、边;然后利用正余弦定理、勾股定理、三角函数的定义建立关于边角的关系式,并进行边角互化,将目标式用只含有边、角的式子表示出来;再通过三角恒等变换将目标式化简,即可运用三角函数的单调性和有界性求得目标式的最值.
解法1.设AD=DC=a,∠BCA=α,
则∠BAC=120°-α,
过点B作BF⊥AC于点F,过D作DE∥BF,以D为原点、AC为x轴、DF为y轴建立平面直角坐标系,如图3所示,
所以α-30°≤45°,α≤75°,
所以∠ACB的最大值为75°.
我们先根据三角形的特征建立平面直角坐标系;然后求得各个点、向量的坐标,以及各条线段的长,即可根据正弦定理、相似三角形的性质建立边角关系式,从而得到关于角α的三角函数式;再对其化简,就能根据正弦函数的有界性和单调性顺利求得角α的最值.
解法2.过点D作DE⊥AC,以D为原点,AC为x轴,DE为y轴建立平面直角坐标系,如图3所示.设AD=DC=a,∠BCA=α,则∠BAC=120°-α.
可得A(a,0),C(-a,0),B(4cosα-a,4sinα),
下同解法1.
解法1与解法2较为相似,都是通过建立直角坐标系,求得目标式的表达式,运用三角函数的性质求得最值.不同的是,解法2是根据直线的方程来求得线段DE的表达式,从而得到目标式.可见,三角函数的性质是求解三角形最值问题的重要工具.同学们在解题时,要注意将问题与角、三角函数的性质关联起来.
总之,解答三角形最值问题,要注意:(1)灵活运用正余弦定理、三角函数的定义、向量、直线的方程等来建立边角关系;(2)注意挖掘三角形中关于边、角的隐含条件;(3)学会运用发散性思维,将问题与解三角形、三角函数、圆、直线的方程等知识关联起来,以寻找到不同的解题思路.
