基于最优样本集在线模糊最小二乘支持向量机的飞行冲突网络态势预测

温祥西，彭娅婷，毕可心，衡宇铭，吴明功*

基于最优样本集在线模糊最小二乘支持向量机的飞行冲突网络态势预测

温祥西1，2，彭娅婷1，2，毕可心3，衡宇铭1，2，吴明功1，2*

（1.空军工程大学 空管领航学院，西安 710051； 2.国家空管防相撞技术重点实验室，西安 710051； 3.中国人民解放军95703部队，云南 陆良 655600）（ ∗ 通信作者电子邮箱 wuminggong@sohu.com）

针对空中交通系统运行周期性和时变性的特点，结合复杂网络理论和模糊最小二乘支持向量机（LSSVM），提出一种基于最优样本集在线模糊最小二乘支持向量机（OTSOF-LSSVM）的飞行冲突网络态势预测方法。首先，基于三维的速度障碍法构建飞行冲突网络模型，并根据航空器的位置、航向和速度判断冲突；其次，分析飞行冲突网络拓扑指标的演化时间序列，得到与预测时刻在时间和距离上相关的样本组成最优样本集；最后，采用在线模糊LSSVM训练得到预测模型，并在模型更新过程中通过分块矩阵思想简化更新过程，提高算法效率。实验结果表明，所提方法能够快速、准确地预测空中态势，为管制员掌握空中交通的发展情况提供参考，并辅助进行冲突的预先调配。

飞行冲突；复杂网络；最小二乘支持向量机；态势预测

0 引言

近年来，航空工程飞速发展，空中交通运输业也取得了长足的进步。虽然空中交通的安全性已经得到了业界较为广泛的认可，但航空器在空中高速运行，航空器间的飞行冲突仍然是不可避免的问题。对于已发生的飞行冲突，管制员处理的时间紧迫，调配难度大，如果航空器在空中出现险情，将造成严重的后果。

如果能预知空情变化趋势，在冲突发生前就进行规划，将有效减少飞行冲突的发生。因此态势预测的相关技术对于空中交通的安全运行尤为重要。空中交通预测的相关技术主要包括流量预测、轨迹预测、延误预测、管制员负荷预测和冲突风险预测等。有关空中交通流量预测的研究较为成熟，Lin等［1］应用网格地图方法将整个空中交通流情况编码为交通流矩阵，提出一种基于深度学习的端到端空中交通流预测模型，可以预测不同飞行高度下的流量分布，具有一定的准确度和稳定性；Gui等［2］将分布式的ADS-B数据信息映射到航线上，对不同城市之间的空中交通流量进行统计和预测，长短期记忆 （Long Short-Term Memory， LSTM）网络对该模型的预测效果较好；Zhang等［3］基于ADS-B数据、相空间重构（Phase Space Reconstruction， PSR）和极限学习机（Extreme Learning Machine， ELM）算法建立了高维的空中交通流量时间序列预测模型，数据表明，交通流在状态稀疏时混沌程度较低。空中交通管理正朝着基于航迹的操作模式发展，轨迹预测将在这一过程中发挥关键作用，并具备发展潜力。Verdonk Gallego等［4］提出了一种飞机之间的概率水平相互依赖测度，该测度能在考虑操作因素的基础上，通过机器学习算法预测航空器的垂直剖面轨迹；Pang等［5］将确定性神经网络模型扩展为考虑不确定性的贝叶斯深度学习模型，用于考虑不同天气影响下的航迹预测。航班延误预测能够提升空中交通的可靠性和管理有效性，降低延误带来的损失［6］。吴仁彪等［7-8］提出了基于深度挤压和激励（Squeeze-and-Excitation， SE）以及基于轻量级卷积注意力模块（Convolutional Block Attention Module， CBAM）的两种航班延误预测模型——SE-CondenseNet和CBAM-CondenseNet，融合航班信息与机场数据，融合后的数据能在特征提取过程中实现特征重新标定，同时加深各层之间的信息传递，避免梯度损失。在管制员负荷的预测方面，刘继新等［9］根据管制员的应激行为筛选出七个指标，建立了基于累积Logistic的管制员应激预测模型，该模型能准确预测管制员的应激程度；王洁宁等［10］提出了基于蒙特卡罗马尔可夫的警觉性概率预测方法，通过Logistic函数，能够预测不同时刻管制员的警觉概率；在冲突风险预测方面，王岩韬等［11-12］对10年来民航的风险事件进行系统分析，确定风险指标，构建了动态贝叶斯网络航班运行过程预测模型，并使用风控系统中的数据对模型参数进行修正。

随着复杂性科学研究的深入，复杂网络被用于空中交通管制的态势预测中。付凯等［13］提出基于模态复现的网络态势预测方法，得到网络态势具有短程相关性、幂律性和群聚性等变化规律。Saâdaoui等［14］提出一种耦合前馈神经网络与非线性最小二乘回归曲线拟合的方法，对空中交通时间序列进行多步预测；王超等［15］基于邻近相点演化提出改进的加权一阶局域预测方法，该方法通过构建误差序列对预测结果进行修正，使预测的精度有所提高；李昂等［16］基于管制-飞行状态相依网络模型，使用LSTM神经网络对网络的拓扑指标时间序列进行预测，结果表明，自由飞行条件下网络时间序列的预测难度更高。进行预测时，神经网络等传统的学习方法由于采用经验风险最小化原则，需要的训练样本数据量大，并且容易出现过学习，使模型的推广能力下降。支持向量机（Support Vector Machine， SVM）模型基于结构风险最小化原则［17-18］，具有较好的泛化能力，解决非线性、高维的小样本数据的能力较强；但潜在飞行冲突的空域是一个时变的系统，飞行冲突网络也会随着空中交通态势的变化而变化，传统的SVM模型对空中交通态势实时预测的效果较差。刘双印等［19］使用在线SVM模型进行预测，通过滑动时间窗口更新训练样本，但相较于求解二次规划问题，SVM模型训练的计算量较大，难以保证预测的实时性。最小二乘支持向量机（Least Squares Support Vector Machine， LSSVM）算法具备SVM的大部分优点［20］，它的训练相当于对线性方程组进行求解，能明显提高模型的训练速度。

针对空中交通的运行态势，本文建立了飞行冲突网络模型，并根据时间相关性和距离相关性构建最优样本集作为模型的训练集，提出基于最优样本集的在线模糊最小二乘支持向量机（Optimal Training Set Online Fuzzy-Least Squares Support Vector Machine， OTSOF-LSSVM）飞行冲突网络态势预测方法。该方法结合复杂网络的特征参数以及飞行冲突网络的实际意义，选择能够反映飞行冲突态势的集聚系数、平均路径长度、鲁棒性和网络效率四项指标进行分析预测。预测模型的更新采用分块矩阵和在线迭代的思想，能实现飞行冲突网络态势的在线预测。

1 飞行冲突网络

本文将飞行冲突网络模型拓展到三维，加入高度信息。现对三维模型作出如下定义：

1.1　网络连边

网络中节点之间构成连边需要满足以下两个条件：1）位置邻近，即两架航空器之间的间隔小于一定范围时，可能会发生冲突；2）满足速度障碍关系，即假设一架航空器静止，为它设置保护区，另一架航空器与它相对速度的方向在速度障碍锥内部。

图1　位置探测区

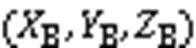
航空器节点间建立连边需要通过速度障碍模型进行第二次判断。相较于车辆和机器人，航空器进行机动的空域是一个三维空间，所以二维的速度障碍法无法适应航空器所有的机动行为，需拓展至三维，如图2所示。

其中：表示相对速度与航空器A和B的位置向量的夹角；表示A和B之间的距离。

1.2　网络边权

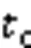
综上，定义网络边权

根据以上规则，生成如图3所示的飞行冲突网络。

图3　飞行冲突网络示意图

图3所示空域中共有6架航空器1～6，其中1号和2号航空器运行在上层高度层中，在图中高度为0.3 km；5号和6号航空器运行在下层高度层中，在图中高度为0；3号和4号航空器运行在两个高度层之间，3号航空器处于爬升状态，4号航空器处于下降状态。

图3显示，1号和5号航空器潜在的冲突数为2，2、3、4和6号航空器潜在1个飞行冲突。飞行冲突网络中航空器之间的冲突关系还可以由权重矩阵表示，图3网络对应的矩阵为：

2 样本集构建

在构建最优样本集时，首先要选取飞行冲突网络的拓扑指标，对样本进行采样，构成网络态势时间序列；随后进行相空间重构，选取时间相关和距离相关样本组成最优样本集，该样本集用于在线模糊最小二乘支持向量机（Online Fuzzy Least Squares Support Vector Machine， OF-LSSVM）的训练以及网络态势的预测。

2.1　态势指标选取

在选择预测指标时，要尽量选取能够反映网络某方面特征的指标，并保证各指标之间具有一定的独立性。对于飞行冲突而言，在设计指标时需要考虑到网络的复杂性、鲁棒性和连通程度，同时还要考虑航空器之间冲突的数量和强度。因此，选取集聚系数、平均路径长度、鲁棒性和网络效率这4项指标，能较全面地反映空域中飞行冲突局部和整体的特性。

1）集聚系数。

节点的集聚系数表示该节点的邻居节点也互为邻居节点的比率，它实际反映了节点邻居之间的聚集情况。飞行冲突网络是相似权网络，连边的权重越高，节点之间联系得就越紧密，所以飞行冲突网络中节点的集聚系数为：

2）平均路径长度。

道路指网络中连接两个节点的连边集合；路径长度是指所有节点之间的最短路径距离。对于相似权网络而言，两节点的路径长度表示为：

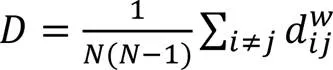
3）鲁棒性。

网络的鲁棒性定义为当网络节点因受到攻击或发生错误而失效时，网络能够维持它本身正常功能的能力，同时它反映了系统的抗扰和抗毁性能，飞行冲突网络的鲁棒性计算如下：

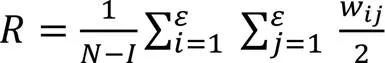
4）网络效率。

网络效率指在信息交互的过程中，沟通渠道的结构形式，是对网络中信息交互能力进行度量的指标。飞行冲突网络为相似权网络，它的网络效率表示为：

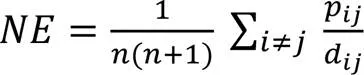
2.2　相空间重构

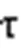
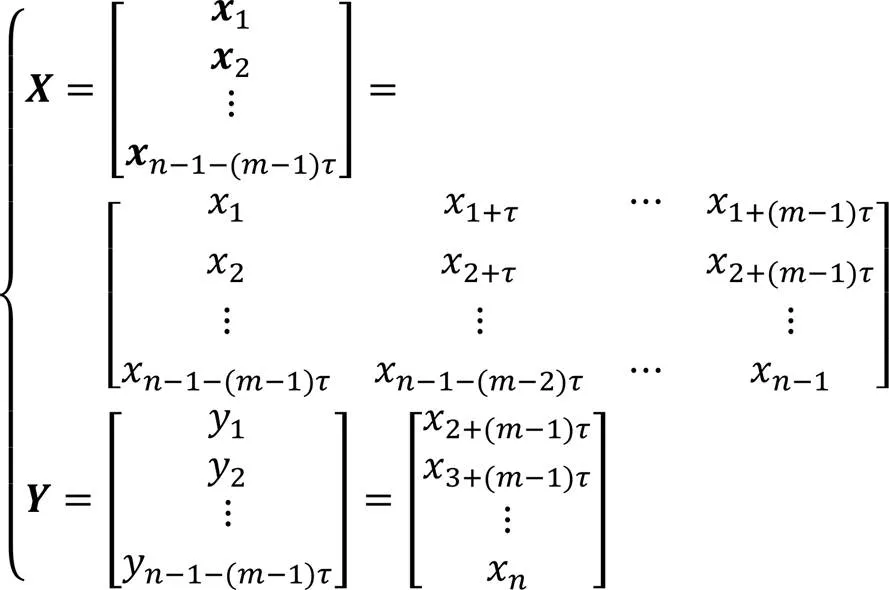
2.3　最优样本集

混沌的时间序列中，样本与预测样本的标准化欧氏距离越接近，该样本所包含的信息与预测样本相关性就越高［20］。由于混沌的时间序列具有自相似特性，这些与预测样本欧氏距离接近的样本便处于预测样本的几何邻域轨道之中，所以这些样本发展的趋势与预测样本也是相似的。可以说在混沌时间序列中预测样本与训练样本之间是距离相关的。因此，与预测样本欧氏距离较近的样本集中包含着更多的预测信息，这与机器学习的本质也是相符的。

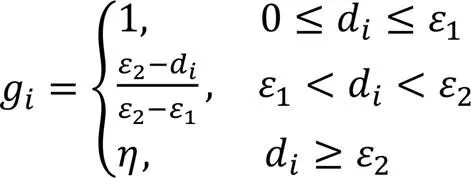
3 OF‑LSSVM

3.1　LSSVM

最小二乘支持向量机（LSSVM）是在支持向量机（SVM）的基础上提出的。SVM是一种机器学习方法，通过训练，它能够找到合适的超平面将样本区分为两类，并在分类的过程中使特征边界到最优分类面的距离最大。

图4　SVM原理

如图4所示，1和2为样本的特征边界，为最优分类面。在边界1上方的样本为正类样本，2下方的为负类样本，1与2之间的样本称为正负类样本。可将SVM的训练转化为一个二次规划问题：

其中：为超平面的法向量，确定超平面方向；y表示类别；为维空间中的任意一点；为位移向量，确定超平面相对于原点的位置。

二次规划问题的求解过程比较复杂。LSSVM通过在优化目标中引入最小二乘损失函数，它的约束条件为等式，将二次规划问题转化为线性方程组进行求解，大幅降低了SVM的算法复杂性，并在核函数矩阵为非正定时也能取得较好的预测和分类结果。

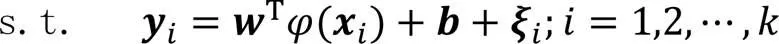
引入Lagrange函数求解该最优化问题：

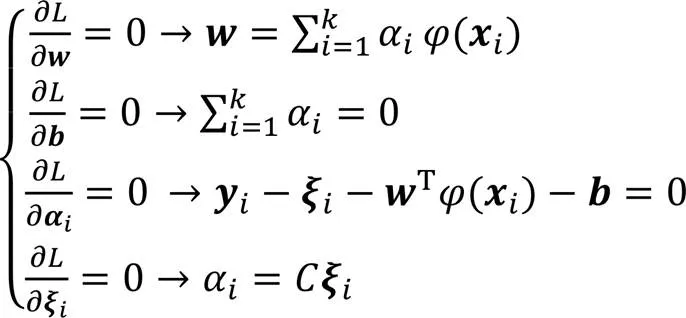
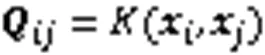
通过求解矩阵方程（21）可得出向量和的值，代入式（19）可得基于LSSVM的飞行冲突网络飞行态势回归预测模型：

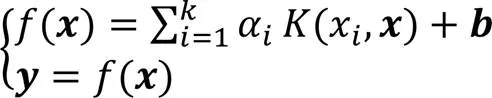
3.2　OF-LSSVM

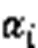
LSSVM虽然训练速度快，但与SVM相比，它的训练精度有所下降，无法保证全局最优解。将模糊隶属度引入LSSVM，根据样本的偏离程度为其设置隶属度值，提升了LSSVM对奇异值引起过拟合的抗干扰能力。

对样本模糊化之后，LSSVM的目标函数可以重写为：

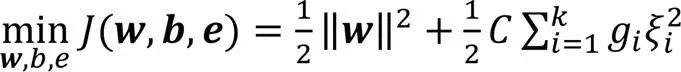
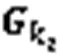
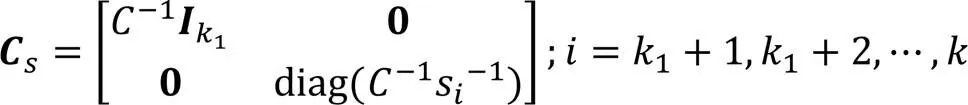
对矩阵进行分块，可以得到：

引理 对于可逆矩阵、和矩阵，，有以下等式成立：

由于每次进行单步预测时间窗口的滑动值为1，在此给出引理的推论：

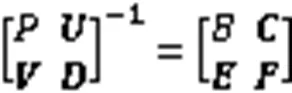
4 预测流程

基于以上分析和方法，建立基于OTSOF-LSSVM的飞行冲突网络态势预测模型，对网络的参数和复杂程度进行预测，流程如图5所示。

图5　飞行冲突网络态势预测模型

步骤1 样本更新。随着飞行冲突网络的演化，采样得到不同网络参数的混沌时间序列，同时时间窗口进行滑动，更新样本。

步骤4 建立在线预测模型。选择核参数和惩罚因子，使用FLSSVM对最优样本集进行在线迭代训练，得到预测模型。

步骤5 输出单步预测结果。向模型中输入预测样本，输出得到预测结果。

步骤6 网络态势更新，重复步骤1～5，输出相对应的预测结果。

5 实验与仿真分析

在100 km×100 km×0.3 km的模拟空域中，对初始随机生成的45架航空器进行演化，演化规则如下：每隔6 s，将会有航空器以50%的概率从高度层的各边界处进入该空域，航空器的航向角任意，假设航空器在该空域飞行过程中不会改变水平航向角，航空器的速度取值范围为［700，850］ km/h，假设航空器改变高度层的概率为1/3，初始的演化场景如图6所示。

图6　演化的初始场景

5.1　混沌性检验

在初始条件下，基于网络的演化规则对网络进行2 000次演化，并分别截取演化1次（6 s）、10次（1 min）、100次（10 min）和1 000次（100 min）的飞行冲突网络，如图7所示；计算每步演化后的集聚系数、平均路径长度、鲁棒性和网络效率，如表1所示，得到这四项网络指标的时间序列；分别截取表1各指标时间序列中第1 200～1 400次演化的数值，绘制成折线图如8所示。

表1　网络指标时间序列

由图8可以看出，网络在演化的过程中，各指标的演化趋势具有一定的相似性，但也存在差异。四项指标整体的变化趋势为“上升-下降-上升“；集聚系数和鲁棒性波形的变化趋势相似度较高；平均路径长度和网络效率波形的振动频率相近。在第一个整体的“上升-下降”峰处（约为第1 220～1 320次演化），网络效率的波形为山峰状，集聚系数和网络鲁棒性则有“下降-上升”的谷趋势，整体波形有所下陷，而平均路径长度在此处的波形呈现为幅度相近的波动。

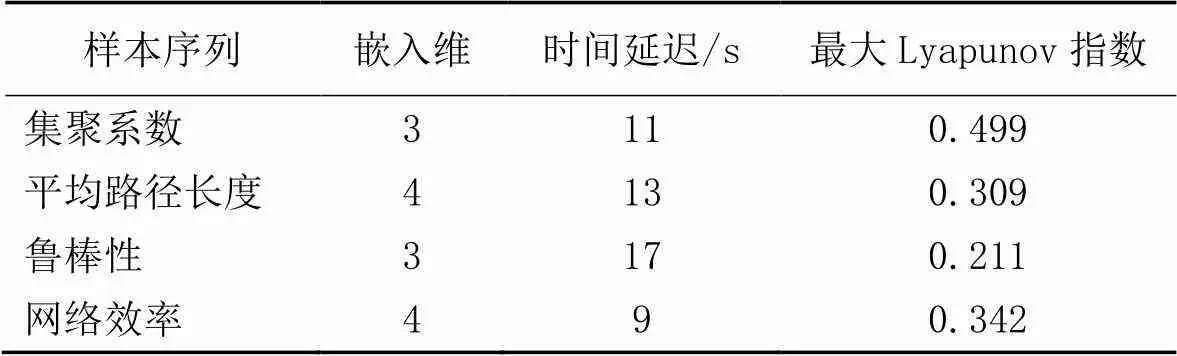
表2　各时间序列的最大Lyapunov指数

图7　网络演化过程示意图

图8　网络指标演化情况

5.2　预测对比仿真

从仿真实验结果可以看出四种方法均能够较好地预测各项态势指标。通过对比基于OTSOF-LSSVM的算法与其他三种算法在四项指标预测的变化情况可以得出，基于OTSOF-LSSVM的算法预测的网络性能指标更准确，更接近实际数值。这些算法中，基于OTSOF-LSSVM的算法预测效果最好，LSSVM算法和LSTM算法次之，神经网络的预测效果最差。这是由于本文方法在训练过程中对训练样本进行了选择，预测模型依据预测样本更新，所以得到的预测效果最好；LSSVM、LSTM方法受与预测样本相关性较弱的训练样本影响，预测效果稍差；神经网络方法采用经验风险最小化原则，在训练样本数较小的情况下预测效果最差。

具体分析本文方法的预测效果，通过预测结果和实际值的变化折线进行对比得到，OTSOF-LSSVM模型对四项指标预测的准确性整体较高，对网络指标上升、下降的趋势预测准确。在2001到2100次演化中，飞行冲突网络的复杂程度出现了2次抬升，分别为203 min到206 min出现了一次大抬升和209 min左右出现的一次小抬升。需要重点对第一次的冲突加剧情况进行关注和预防。

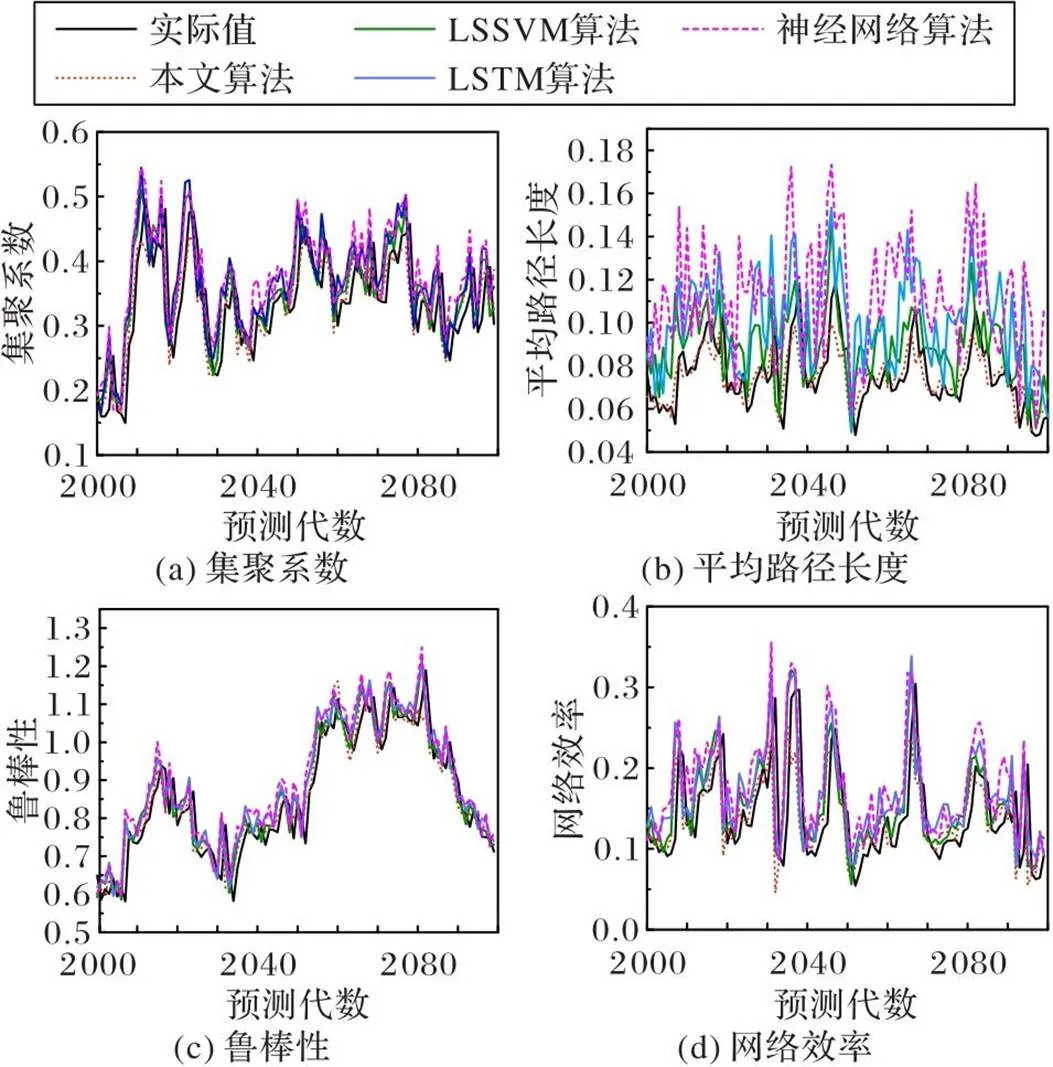
图9　各指标的预测结果

5.3　误差分析

为了判断OTSOF-LSSVM模型对飞行冲突网络指标预测的精度，计算了预测结果的相对误差，结果如图10所示。由图10可以看出：OTSOF-LSSVM模型对网络的集聚系数和平均路径长度的预测精度高，误差整体在±5%波动；而对鲁棒性和网络效率的预测误差相对更大，观察图9（a）中集聚系数第2 019次和图9（d）中网络效率第2 069、2 071次的演化和预测情况，实际值与预测值的大小和变化趋势均相近，相对误差主要是由演化中网络指标下降、指标实际值过小造成。这种情况下的网络复杂性低，意味着空域中的航空器和冲突较少，对空中交通安全的威胁性小。

图10　四项指标的相对误差

5.4　可行性验证

为了验证模型的可行性，进一步设置三个场景生成不同数据集进行仿真实验。设置空域的范围、航空器数量、飞行态势演化规则和数据集样本数如表3所示，改变的演化规则有航空器进入空域概率、间隔时间和改变高度层的概率。

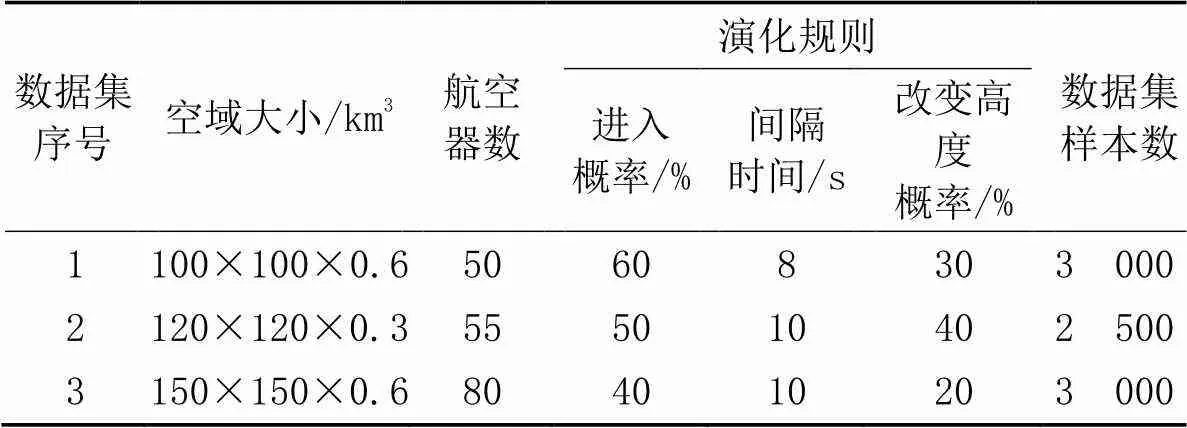
表3　数据集生成规则

使用OTSOF-LSSVM模型对表3这三组演化情况的数据集进行训练，并预测后续100次演化的网络态势情况，计算预测结果的相对误差，结果如图11所示。从图11可以看出，利用OTSOF-LSSVM模型对三组不同的数据集进行预测的相对误差整体在±8%波动，效果较好，数据集样本量大，数据集多样性好，进一步验证了OTSOF-LSSVM模型具有很强的泛化性。

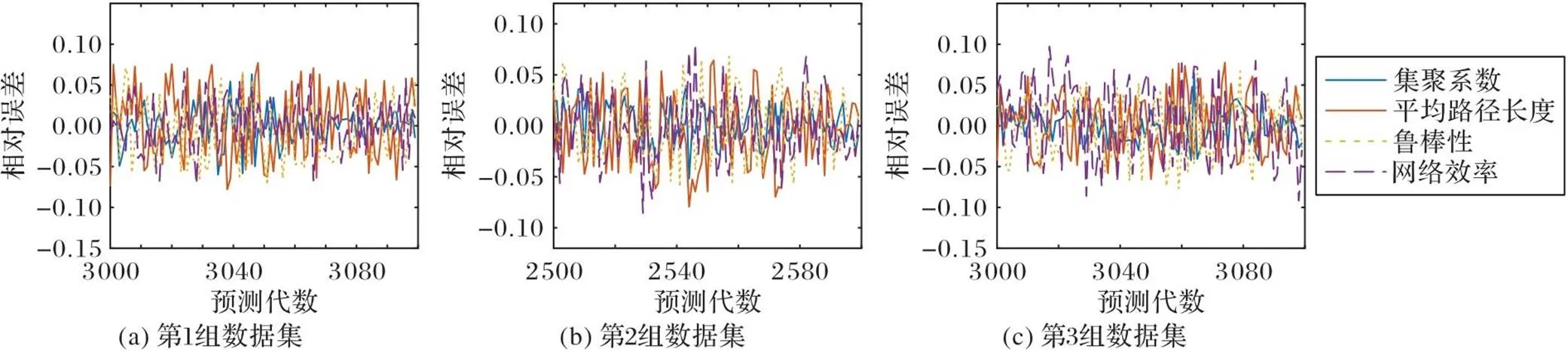
图11　三组数据集的预测相对误差

6 结语

本文使用C-C法和Wolf法验证了飞行冲突网络指标的时间序列具有混沌特性，并在该特性的基础上提出基于OTSOF-LSSVM的飞行冲突网络态势预测方法，使用相空间重构后的最优样本集对模型进行在线训练，使得到的预测模型能够兼顾准确性、实时性和可行性要求。仿真结果表明，模型对选取的四项网络指标相较于其他三种对比方法预测精度更高，能够准确预测飞行冲突网络复杂性的变化情况。管制员可以根据预测的结果对空中交通的复杂情况进行预知和预防，结合当前空域实际提前进行航空器冲突的调配工作，减少事故征候和飞行冲突的发生。

[1] LIN Y， ZHANG J W， LIU H. Deep learning based short-term air traffic flow prediction considering temporal-spatial correlation［J］. Aerospace Science and Technology， 2019， 93： No.105113.

[2] GUI G， ZHOU Z， WANG J， et al. Machine learning aided air traffic flow analysis based on aviation big data［J］. IEEE Transactions on Vehicular Technology， 2020， 69（5）： 4817-4826.

[3] ZHANG Z， ZHANG A， SUN C， et al. Research on air traffic flow forecast based on ELM non-iterative algorithm［J］. Mobile Networks and Applications， 2021， 26（1）： 425-439.

[4] VERDONK GALLEGO C E， GÓMEZ COMENDADOR V F， AMARO CARMONA M A， et al. A machine learning approach to air traffic interdependency modelling and its application to trajectory prediction［J］. Transportation Research Part C： Emerging Technologies， 2019， 107： 256-386.

[5] PANG Y， ZHAO X， YAN H， et al. Data-driven trajectory prediction with weather uncertainties： a Bayesian deep learning approach［J］. Transportation Research Part C： Emerging Technologies， 2021， 130： No.103326.

[6] 王春政，胡明华，杨磊，等. 空中交通延误预测研究综述［J］. 系统工程与电子技术， 2022， 44（3）：863-874.（WANG C Z， HU M H， YANG L， et al. Review on air traffic delay prediction［J］. Systems Engineering and Electronics， 2022， 44（3）： 863-874.）

[7] 吴仁彪，赵婷，屈景怡. 基于深度SE-DenseNet的航班延误预测模型［J］. 电子与信息学报， 2019， 41（6）：1510-1517.（WU R B， ZHAO T， QU J Y. Flight delay prediction model based on deep SE-DenseNet［J］. Journal of Electronics and Information， 2019， 41（6）：1510-1517.）

[8] 吴仁彪，赵娅倩，屈景怡，等. 基于CBAM-CondenseNet的航班延误波及预测模型［J］. 电子与信息学报， 2021， 43（1）：187-195.（WU R B， ZHAO Y Q， QU J Y， et al. Flight delay propagation prediction model based on CBAM-CondenseNet［J］. Journal of Electronics and Information， 2021， 43（1）： 187-195.）

[9] 刘继新，曾逍宇，尹旻嘉，等. 基于累积Logistic回归模型的管制员应激程度预测［J］. 重庆交通大学学报（自然科学版）， 2019， 38（3）：97-102， 115.（LIU J X， ZENG X Y， YIN M J， et al. Stress level prediction of controller based on cumulative logistic regression model［J］. Journal of Chongqing Jiaotong University （Natural Science）， 2019， 38（3）： 97-102， 115.）

[10] 王洁宁，张钰涵，冀姗姗. 基于马尔科夫蒙特卡罗的管制员警觉概率预测［J］. 安全与环境学报， 2020， 20（4）：1412-1420.（WANG J N， ZHANG Y H， JI S S. Probability prediction of the controller’s status-in-situ alertness based on Markov chain Monte Carlo［J］. Journal of Safety and Environment， 2020， 20（4）： 1412-1420.）

[11] 王岩韬，刘宏，唐建勋，等. 动态预测技术在航班运行风险中的应用［J］. 控制与决策， 2019， 34（9）：1946-1954.（WANG Y T， LIU H， TANG J X， et al. Dynamic prediction technology in the application of flight operation risk［J］. Control and Decision， 2019， 34（9）： 1946-1954.）

[12] 王岩韬，李景良，谷润平. 基于多变量混沌时间序列的航班运行风险预测模型［J］. 工程科学学报， 2020， 42（12）：1664-1673.（WANG Y T， LI J L， GU R P. Flight operation risk prediction model based on the multivariate chaotic time series［J］. Journal of Engineering Science， 2020， 42（12）： 1664-1673.）

[13] 付凯，夏靖波，申健. 基于复杂网络拓扑性质的网络态势预测方法［J］. 华中科技大学学报（自然科学版）， 2018， 46（1）：42-48.（FU K， XIA J B， SHEN J. Network situation prediction method based on topological properties of complex network［J］. Journal of Huazhong University of Science and Technology （Natural Science Edition）， 2018， 46（1）： 42-48.）

[14] SAÂDAOUI F， SAADAOUI H， RABBOUCH H. Hybrid feedforward ANN with NLS-based regression curve fitting for US air traffic forecasting［J］. Neural Computing and Applications， 2020， 32（14）： 10073-10085.

[15] 王超，朱明，赵元棣. 基于改进加权一阶局域法的空中交通流量预测模型［J］. 西南交通大学学报， 2018， 53（1）：206-213.（WANG C， ZHU M， ZHAO Y D. Air traffic flow prediction model based on improved adding-weighted one-rank local-region method［J］. Journal of Southwest Jiaotong University， 2018， 53（1）： 206-213.）

[16] 李昂，聂党民，温祥西，等. 管制-飞行状态相依网络演化过程研究［J］.航空学报， 2021， 42（9）： No.324726.（LI A， NIE D M， WEN X X， et al. Evolution process of control-aircraft state dependent network［J］. Acta Aeronautica et Astronautica Sinica， 2021， 42（9）： No.324726.）

[17] 张学工. 关于统计学习理论与支持向量机［J］. 自动化学报， 2000， 26（1）：32-42.（ZHANG X G. Introduction to statistical learning theory and support vector machines［J］. Acta Automatica Sinica， 2000， 26（1）：32-42.）

[18] 丁世飞，齐丙娟，谭红艳. 支持向量机理论与算法研究综述［J］. 电子科技大学学报， 2011， 40（1）：2-10.（DING S F， QI B J， TAN H Y. An overview on theory and algorithm of support vector machines［J］. Journal of University of Electronic Science and Technology of China， 2011， 40（1）： 2-10.）

[19] 刘双印，徐龙琴，李道亮，等. 基于时间相似数据的支持向量机水质溶解氧在线预测［J］. 农业工程学报， 2014， 30（3）：155-162.（LIU S Y， XU L Q， LI D L， et al. Online prediction of dissolved oxygen in water quality based on support vector machine with time series similar data［J］. Transactions of the Chinese Society of Agricultural Engineering， 2014， 30（3） ：155-162.）

[20] 田中大，高宪文，石彤. 用于混沌时间序列预测的组合核函数最小二乘支持向量机［J］. 物理学报， 2014， 63（16）： No.160508.（TIAN Z D， GAO X W， SHI T. Combination kernel least squares support vector machine for chaotic time series forecasting［J］. Acta Physica Sinica， 2014， 63（16）： No.160508.）

[21] 陆锦军，王执铨. 基于混沌特性的网络流量预测［J］. 南京航空航天大学学报， 2006， 38（2）：217-221.（LU J J， WANG Z Q. Prediction of network traffic flow based on chaos characteristics［J］. Journal of Nanjing University of Aeronautics and Astronautics， 2006， 38（2）： 217-221.）

[22] 胡瑜，陈涛. 基于C-C算法的混沌吸引子的相空间重构技术［J］. 电子测量与仪器学报， 2012， 26（5）：425-430.（HU Y， CHEN T. Phase-space reconstruction technology of chaotic attractor based on C-C method［J］. Journal of Electronic Measurement and Instrumentation， 2012， 26（5）： 425-430.）

[23] 林玲，陈福集，谢加良，等. 基于改进灰狼优化支持向量回归的网络舆情预测［J］. 系统工程理论与实践， 2022， 42（2）：487-498.（LIN L， CHEN F J， XIE J L， et al. Prediction of network public opinion prediction based on improved grey wolf optimization support vector regression［J］. Systems Engineering Theory and Practice， 2022， 42（2）： 487-498.）

Situation prediction of flight conflict network based on online fuzzy least squares support vector machine with optimal training set

WEN Xiangxi1，2， PENG Yating1，2， BI Kexin3， HENG Yuming1，2， WU Minggong1，2*

（1，，’710051，；2，’710051，；395703，655600，）

Concerning the periodicity and time-varying characteristics of air traffic system operation， a flight conflict network situation prediction method based on Optimal Training Set Online Fuzzy-Least Squares Support Vector Machine （OTSOF-LSSVM） was proposed by combining complex network theory and fuzzy Least Squares Support Vector Machine （LSSVM）. Firstly， a flight conflict network model was constructed based on the three-dimensional velocity obstacle method， and conflicts were judged according to the positions， headings and velocities of the aircrafts. Then， the evolution time series of topology indicators of flight conflict network were analyzed to obtain the optimal training set which consisted of samples related to the predicted moment in time and distance. Finally， a prediction model was obtained by online fuzzy LSSVM training， and the idea of block matrix was used to simplify the updating process and improve the efficiency of the algorithm. Experimental results show that the proposed method can quickly and accurately predict the air situation， provide reference for controllers to master the development of air traffic， and assist the pre-deployment of conflicts.

flight conflict; complex network; Least Squares Support Vector Machine (LSSVM); situation prediction

1001-9081（2023）11-3632-09

10.11772/j.issn.1001-9081.2022101605

2022⁃10⁃26；

2023⁃01⁃03；

国家自然科学基金资助项目（71801221）。

温祥西（1984—），男，江苏连云港人，副教授，博士，主要研究方向：空管自动化； 彭娅婷（1995—），女，湖南株洲人，硕士研究生，主要研究方向：扇区划设和优化、冲突探测与解脱； 毕可心（1997—），男，陕西西安人，硕士研究生，主要研究方向：航空管制指挥与安全； 衡宇铭（1998—），男，河南新乡人，硕士研究生，主要研究方向：交通运输； 吴明功（1966—），男，山东潍坊人，教授，硕士，主要研究方向：交通运输工程、航空管制指挥与安全。

TP301.6； V355

A

2023⁃01⁃09。

This work is partially supported by National Natural Science Foundation of China （71801221）.

WEN Xiangxi， born in 1984， Ph. D.， associate professor. His research interests include air traffic control automation.

PENG Yating， born in 1995， M. S. candidate. Her research interests include sector planning and optimization， conflict detection and resolution.

BI Kexin， born in 1997， M. S. candidate. His research interests include air traffic control command and safety.

HENG Yuming， born in 1998， M. S. candidate. His research interests include transportation.

WU Minggong， born in 1966， M. S.， professor. His research interests include transportation engineering， air traffic control command and safety.