基于大地距离计算相似度的海上目标轨迹预测

赵一鉴，林利，王茜蒨，4*，闻鹏，杨东

基于大地距离计算相似度的海上目标轨迹预测

赵一鉴1，2，林利3，王茜蒨1，2，4*，闻鹏5，杨东5

（1.北京理工大学 光电学院，北京 100081； 2.信息光子技术工业和信息化部重点实验室（北京理工大学），北京 100081； 3.中国人民解放军32011部队，北京 100094； 4.北京理工大学长三角研究院，浙江 嘉兴 314033； 5.航天恒星科技有限公司，北京 100095）（ ∗ 通信作者电子邮箱qqwang@bit.edu.cn）

目前基于相似度的移动目标轨迹预测算法一般根据数据的时空特性进行分类，无法体现算法自身的特点，为此提出一种基于算法特征的分类方法。轨迹相似度算法通常需要先计算两点之间的距离，再开展后续计算，而常用的欧氏距离（ED）只适用于目标在小区域范围内移动的问题。针对现有基于相似度的轨迹预测算法无法适用于移动范围比较大的海上目标轨迹预测的问题，提出使用大地距离代替ED进行相似度计算。首先，对轨迹数据进行预处理和分段；其次采用离散弗雷歇距离（FD）作为相似性度量；最后，利用模拟数据和实际数据进行测试。实验结果表明，当海上目标移动范围较大时，采用ED算法可能会得到不正确的预测结果，而所提算法可输出正确的目标轨迹预测结果。

轨迹相似度；轨迹预测；欧氏距离；大地距离；弗雷歇距离

0 引言

移动目标轨迹预测指根据历史数据预测目标在未来的运动轨迹，它对于目标的位置预测、目标异常行为检测、智能交通监管、海上船只防撞预警等具有重要意义。

目前的移动目标轨迹预测方法可分为三类：基于概率统计的方法、基于机器学习的方法和基于轨迹相似度的方法。其中，基于概率统计的预测方法包括卡尔曼滤波、差分自回归移动平均、马尔可夫模型、高斯混合模型、贝叶斯网络等，优点是数学方法成熟、应用较广，但预测精度严重依赖于轨迹数据本身的间隔和误差，且无法对长时间的轨迹进行精准预测［1］。基于机器学习的预测算法包括神经网络和深度学习，深度学习算法包括循环神经网络、长短期记忆、极限学习机等，优点是预测精度较高，但所需的训练数据量大、算法可解释性低［1］。此外，还有一些基于混合模型的预测算法，如概率统计与深度学习相结合的方法［2］、马尔可夫与神经网络相结合的方法［3］等，通过融合不同的预测方法来提高预测精度。无论是概率统计还是机器学习算法，都需要大量数据进行概率分析或机器训练；当历史数据较少时，预测效果都不佳。基于轨迹相似度的预测方法假设目标运动遵循一定的周期或规律，根据观测到的一段轨迹，从历史轨迹中寻找一条最相似的轨迹，并把此轨迹中的后续数据作为目标预测轨迹。当目标历史数据较少时，这种方法不失为一种可行的方法。谢彬等［4］利用轨迹相似度算法对移动目标进行轨迹预测，王爱兵等［5］利用轨迹相似度算法对行人轨迹进行预测，张春玮等［6］利用轨迹相似度算法对船舶轨迹进行聚类分析和异常检测。轨迹相似度算法在其他方面的研究应用包括出租车合乘、公交线路调整、轨迹社区发现、伴随人员推荐等［7-10］。

轨迹相似度的算法很多。Magdy等［11］根据轨迹数据是否包含时间信息，把相似度算法分为空间相似度算法和时空相似度算法两大类。Su等［12］根据轨迹数据是否包含时间信息以及轨迹是连续的还是离散的，把相似度算法分为连续序列、离散序列、连续时空和离散时空四类算法。这两种分类方法更多关注的是数据本身的特性。本文根据算法自身的特点，把轨迹相似度算法分为三类：基于面积特性、基于距离特性和基于运动方向特性。

1）基于面积特性的算法。这类算法的思路是如果两条轨迹重合，两轨迹围成的面积是零；如果轨迹不重合，则面积越小越相似。主要的算法有多线位置距离（Locality In-between Polylines， LIP）。

2）基于距离特性的算法。这类算法的思路是如果两条轨迹是重合的，轨迹之间的距离是零；如果轨迹不重合，则轨迹之间的距离越小相似度越高。轨迹之间的距离既可以是多个点之间的平均距离，也可以是特征点之间的距离。欧氏距离（Euclidean Distance， ED）是最简单常用的一种算法［11-12］，它是两条轨迹上对应点之间距离的平均值，表达式如下：

基于平均距离特性的算法还包括：动态时间规整（Dynamic Time Warping， DTW）、最长公共子序列（Longest Common Sub-Sequence， LCSS）、编辑距离（Edit Distance on Real sequence， EDR）、单向距离（One Way Distance， OWD）、时间扭曲编辑距离（Time Warp Edit Distance， TWED）、带有实数惩罚的编辑距离（Edit distance with Real Penalty， ERP）、融合距离（Merge Distance， MD）等［11-12］。

基于两轨迹上特征点距离的算法包括豪斯多夫距离（Hausdorff Distance， HD）、弗雷歇距离（Fréchet Distance， FD）、最近邻距离（Closest-Pair Distance， CPD）等。HD是两条轨迹中最近点距离的最大值［11-12］，它的值越小，两条轨迹越相似。FD算法与HD算法类似，只不过在计算最小距离时考虑了两条曲线的流动，不考虑从一个端点回溯到另一个端点的情形［11-12］。FD通常被称为“遛狗距离”，假设一条狗和它的主人在两条不同的路径上行走，FD是连接狗和主人所需的最小绳子长度，也可以把FD看作河流两岸之间的最宽距离。CPD算法也是基于特征点的算法［13］，它是从两条轨迹中找到最近的一对点，它们之间的距离就是最近邻距离，此值越小说明两曲线越接近。

3）基于运动方向的算法。这类算法的思路是如果两条轨迹重合，两轨迹上各点的运动方向是相同的；如果轨迹不重合，则运动方向的夹角越小轨迹越相似。主要的算法包括基于形状相似性的角度度量（Angular Metric for Shape Similarity， AMSS）、基于运动模式字符串的编辑距离（Edit Distance on Movement pattern strings， EDM）、轨迹匹配和运动时空关系匹配（Trajectory match and Moving spatiotemporal relation match， TM）等［11］。

以上轨迹相似度算法是最基本的，很多学者在此基础上对算法进行了改进，以满足不同场合下的实际需求。文献［14］中在HD算法基础上，提出了一种改进的基于时间约束的算法；文献［15］中在DTW算法的基础上结合DNA序列校准算法，提出了适用于不同采样率、对噪声鲁棒的轨迹相似度算法；文献［16］中利用轨迹压缩方法对LCSS算法进行改进，提高了计算速度。此外，还有结合了文本信息的语义轨迹相似度［9］等新的相似度算法不断涌现。

相似度算法一般都需要计算点与点之间的距离，目前采用的都是基于ED，这实际上是平面上两点之间的距离公式。考虑到地球表面是个球面，ED应用于移动范围比较大的海上目标时，预测结果可能不正确，本文以下将进行分析和验证。

1 海上目标轨迹预测问题

考虑地球上纬度相同、经度相差1°的两点，无论这两点在地球表面上的任何地方，应用ED得到的结果都相同。现在考虑两种情形：一种是在赤道上，大地距离是111.3 km；另一种是在纬度45°的地方，大地距离是78.8 km，两者之比大致为1∶cos 45°。为了探究ED和大地距离对轨迹相似度计算的影响，下面以一个简单的模型进行分析，并用FD作为两条轨迹相似度的度量。

图1　目标的运动轨迹

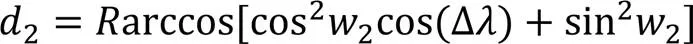
代入式（3）、（4），得：

式（8）可进一步简化为：

式（9）就是ED公式适用的边界条件。为了直观地表明它适用的区域范围，以下给出一个具体的例子。

但对于在海上自由航行的船只来说，由于船只的移动范围大，每段轨迹的长度长，式（9）在某些条件下会得到满足。图1的情形只是一个特殊的例子，但以上的分析计算对目标的轨迹形状并没有特殊要求，目标的轨迹形状可以是任意的，只要在适当的条件下满足式（9），采用ED算法预测的结果就不正确。因此对于海上移动目标的轨迹预测，必须采用大地距离公式。

以上采用的大圆弧长公式是计算大地距离的一种近似方法，考虑到地球是椭球体，为了准确计算两点之间的大地距离，需要采用更精确的算法。现有的用于解决大地主题问题的方法中，有的适用于短距离（400 km以下），有的适用于中距离（400～1 000 km），有的适用于长距离（1 000 km以上），其中比较典型的有勒让德级数公式、高斯平均引数公式和白塞尔公式等［17］。勒让德级数在30 km以下的精度相对高一些，高斯平均引数适合于200 km以下的大地主题解算，白塞尔公式的解算精度与距离长短没有关系，既适用于长距离，也适用于短距离。如果使用Python语言编程，则可直接调用geopy库中的大地距离计算函数。geopy库中提供了两种大地距离计算方法：Vincenty公式和Great Circle公式。Vincenty公式是文森特（Vincenty）于1975年以白塞尔公式为基础，推导出的嵌套系数公式，计算速度较慢，但计算结果更为准确；Great Circle公式是以球心和球面上两点组成的大圆上连接两点的最短弧长距离。经实际测试，Vincenty公式的计算时间大约是Great Circle公式的2倍。由于这两种算法计算时间很短，一般在几十到数百毫秒，因此在各种应用中一般首选Vincenty公式。一个计算大地距离的例子如下所示：

from geopy import distance

p1 = （41， 103）

p2 = （40， 104）

print （distance.distance（p1， p2））

139.698 755 392 749 97 km

在上面的例子中，调用distance函数时缺省的算法就是Vincenty公式。

2 海上目标轨迹预测方法

2.1　算法选择

考虑到FD算法效率较高，应用的场合较多，本文选择FD算法进行海上移动目标轨迹预测。FD算法分为连续FD和离散FD。实际的轨迹数据都是离散的，所谓的连续FD只不过是对离散的轨迹数据进行插值处理使得离散的轨迹变成连续的，两种算法的思路基本相同。考虑到离散FD算法相对简单，便于编程实现，本文采用离散FD算法。它的算法公式如下，详细的介绍见文献［18］。

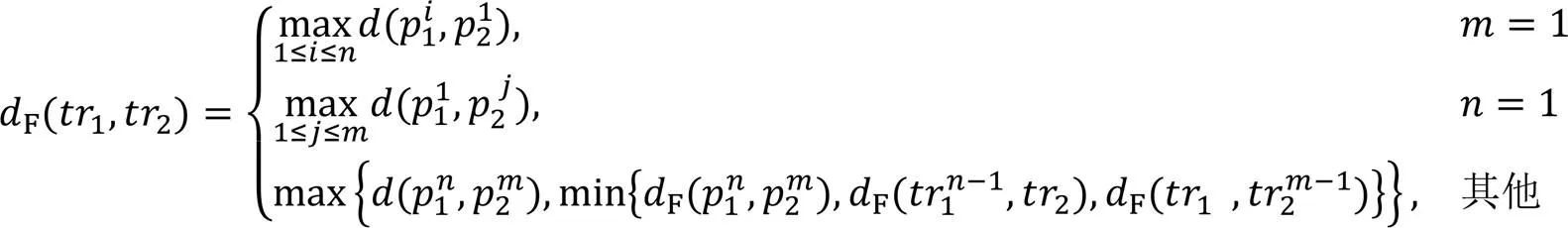
2.2　数据预处理

理想的轨迹数据按时间顺序存放，并且没有重复点和噪声点。实际的数据情况千差万别，如有时会发现存在完全相同的两个数据点，这两个数据点连续存放，可能是数据存放时出现的问题，也可能是信号本身的问题；还有少部分数据不是按时间的先后顺序存放，有时会出现后一数据点的时间比前一个数据点时间靠前的情况。针对这些问题，必须对数据进行预处理，首先去掉多余的相同数据，其次对数据按时间顺序采用快速排序法进行重新排列。对噪声点的处理也是数据预处理的一项重要工作。基于平均距离和面积特性的算法对噪声点有一定的压制作用，基于特征点距离的算法则对噪声点比较敏感，所以必须设法去除噪声点对算法的影响。针对不同的数据特点，选择合适的降噪方法。当数据量较小时，也可以结合人工经验进行判断。

2.3　轨迹分段

由于历史轨迹数据和当前测量数据在数据文件中连续存放，因此必须对数据进行合理的分段，然后计算最后测量时段的轨迹与各个历史分段轨迹的相似度。轨迹分段主要基于数据特点进行。由于目标的运动轨迹并不是连续观测到的，而是在不同的时间段和不同地点观测到的，本文综合考虑距离和时间因素进行分段。如果前后两个相邻数据点的时间差大于某一数值，比如1 d或3 d，则从后一数据点开始认为是一段新的观测数据。其次，考虑到目标是连续移动的，如果前后两个相邻数据点的距离差大于某一阈值时，则认为两个点分属两段数据。轨迹分段的具体算法流程如图2所示。

图2　轨迹分段算法流程

2.4　算法流程

应用FD算法进行轨迹预测的流程如图3所示：首先，进行数据预处理，把数据按时间顺序排好，并去除掉噪声点，存放到数组中；其次，对数据进行分段，分别存放到另外的数组中；接着，把最后一段的轨迹数据和前面的历史轨迹数据逐一进行相似度比较，从中选取FD最小者，此段历史轨迹就是轨迹预测的基础；然后找到最后观测点与相似轨迹上最近的点，此点以后的轨迹就是预测的目标未来轨迹。根据需要也可附加上必要的预测时间信息。

图3　基于FD算法的轨迹预测流程

3 实验与结果分析

采用轨迹相似度算法，对两组模拟数据进行了仿真计算。当数据较多时，数据点密集重合在一起，不便于直观显示预测效果。为此，采用最后观测数据附近的少量数据进行测试。测试结果如图4所示。经过预处理后的轨迹数据按照观测时间顺序依次以数字进行标注。实线（黑色）表示经过分段处理后的子轨迹段，各子轨迹段之间以虚线相连。三角形图例（蓝色）代表最后观测到的子轨迹，圆形图例（红色）代表预测的目标未来轨迹。红色线所在的子轨迹段为算法找到的最相似的轨迹。找到最相似度轨迹后，在预测目标未来运动趋势时，在最相似轨迹上有两种运动可能：向前运动或向后运动。和观测轨迹运动方向一致的就是目标的运动方向。具体方法是：先在最相似子轨迹上找到与最后观测点距离最近的点（图4（a）的20点和图4（b）中的5点），分别计算此点与子轨迹上前后相邻两点的向量（即分别计算图4（a）中20点和19点之间的向量以及20点和21点之间的向量，图4（b）中则是5点与4点和5点与6点之间的向量），再计算观测轨迹上最后两点的向量，它与目标历史轨迹运动向量方向一致（实际中可设为小于90°）的就是预测的目标运动方向。从此点以后直到子轨迹结束的轨迹点就是预测的目标未来轨迹，如图4中的点划线（红色）所示。

图4　模拟数据仿真结果

在以上仿真实验的基础上，采用某移动目标的实际数据进行测试，结果如图5所示，其中三角形图例（蓝色）是最后一段观测数据，圆形图例（红色）是预测的目标未来轨迹。

图5　实际数据测试结果

从图4、5可以直观看出，观测轨迹与最相似轨迹之间的距离比其他轨迹与观测轨迹之间的距离小。假如目标的运动具有周期性规律，采用轨迹相似度算法的预测结果与目标的实际运动轨迹将会很接近。

前面分析讨论了当目标活动范围较大时，采用ED的预测结果有时会不正确，图6展示了这种情况。由于大地距离更真实地反映了球面上两轨迹间的间隔，因而当目标活动区域较大时，应采用大地距离公式。

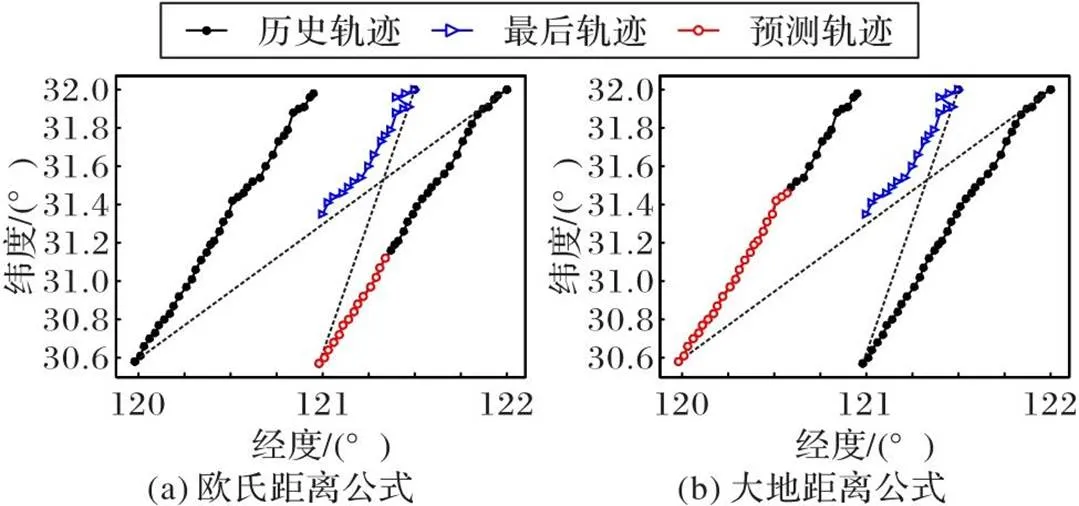
图6　ED和大地距离两种算法预测的不同结果

4 结语

针对目前的轨迹相似度算法分类方法无法体现算法自身特征的问题，本文提出了基于算法特征的分类方法，可简单清晰地区分各类常见算法。本文的分析表明，对于海上船只等在大范围内移动的目标轨迹预测问题，采用ED有时会得到不正确的结果。为避免这种情况，可用大地距离代替ED进行相似度计算。本文在大地距离计算的基础上，应用离散FD算法进行轨迹相似度计算，实现了对海上目标的运动轨迹预测。模拟和实际数据的测试结果表明，算法可输出正确的预测结果。本文方法也适用于草原动物和候鸟迁徙的路线预测等问题。为了进一步提高预测精度，还可考虑对预测轨迹进行距离修正，即计算观测轨迹与最相似轨迹之间的平均距离，然后对预测的每个轨迹点都附加上平均距离。

［1］ 刘文，胡琨林，李岩，等. 移动目标轨迹预测方法研究综述［J］. 智能科学与技术学报， 2021， 3（2）：149-160. （LIU W， HU K L， LI Y， et al. A review of prediction methods for moving target trajectories［J］. Chinese Journal of Intelligent Science and Technology， 2021， 3（2）：149-160.）

［2］ 石庆研，岳聚财，韩萍，等. 基于LSTM-ARIMA模型的短期航班飞行轨迹预测［J］. 信号处理， 2019， 35（12）： 2000-2009. （SHI Q Y， YUE J C， HAN P， et al. Short-term flight trajectory prediction based on LSTM-ARIMA model［J］. Journal of Signal Processing， 2019， 35（12）： 2000-2009.）

［3］ PECHER P， HUNTER M， FUJIMOTO R. Data-driven vehicle trajectory prediction［C］// Proceedings of the 2016 ACM SIGSIM Conference on Principles of Advanced Discrete Simulation. New York： ACM， 2016： 13-22.

［4］ 谢彬，张琨，张云纯，等. 基于轨迹相似度的移动目标轨迹预测算法［J］. 计算机工程， 2018， 44（9）：177-183. （XIE B， ZHANG K， ZAHNG Y C， et al. Trajectory prediction algorithm for mobile target based on trajectory similarity［J］. Computer Engineering， 2018， 44（9）：177-183.）

［5］ 王爱兵，刘亚朋，夏辉，等. 基于轨迹相似度的行人轨迹预测方法研究［J］. 石家庄职业技术学院学报， 2021， 33（2）：5-8. （WANG A B， LIU Y P， XIA H， et al. On the trajectory similarity and prediction of pedestrian trajectory［J］. Journal of Shijiazhuang University of Applied Technology， 2021， 33（2）： 5-8.）

［6］ 张春玮，马杰，牛元淼，等. 基于行为特征相似度的船舶轨迹聚类方法［J］. 武汉理工大学学报（交通科学与工程版）， 2019， 43（3）： 517-521. （ZHANG C W， MA J， NIU Y M， et al. Clustering method of ship trajectory based on similarity of behavior pattern［J］. Journal of Wuhan University of Technology （Transportation Science and Engineering）， 2019， 43（3）： 517-521.）

［7］ 吴玥琳，袁振洲，陈秋芳，等.考虑轨迹相似度的综合客运枢纽出租车合乘方法研究［J］.交通运输系统工程与信息，2020，20（2）：188-195. （WU Y L， YUAN Z Z， CHEN Q F， et al. Taxi pooling method of urban integrated passenger transport hub with trajectory similarity［J］. Journal of Transportation Systems Engineering and Information Technology， 2020， 20（2）： 188-195.）

［8］ 程志华. 通过计算公交线路轨迹相似度检测线路是否调整的方法［J］. 公路交通科技（应用技术版）， 2020（1）： 371-373. （CHENG Z H. A method of detecting whether the bus line should be adjusted by calculating the similarity of bus line trajectory［J］. Journal of Highway and Transportation Research and Development （Applied Technology）， 2020（1）： 371-373.）

［9］ 柳帅. 基于时空和语义相似度的轨迹社区发现方法研究［D］. 沈阳： 东北大学， 2015： 10-11. （LIU S. Research on trajectory community detection based on spatial-temporal similarity and semantic similarity［D］. Shenyang： Northeastern University， 2015： 10-11.）

［10］ 廖闻剑，田小虎，邱秀连. 基于轨迹相似度的伴随人员推荐［J］. 计算机系统应用， 2018， 27（4）： 157-161. （LIAO W J， TIAN X H， QIU X L. Companion recommendation based on trajectory similarity［J］. Computer Systems & Applications， 2018， 27（4）： 157-161.）

［11］ MAGDY N， SAKR M A， MOSTAFA T， et al. Review on trajectory similarity measures［C］// Proceedings of the IEEE 7th International Conference on Intelligent Computing and Information Systems. Piscataway： IEEE， 2015： 613-619.

［12］ SU H， LIU S， ZHENG B， et al. A survey of trajectory distance measures and performance evaluation［J］. The VLDB Journal， 2020， 29（1）： 3-32.

［13］ CAI X. Effective algorithms for the closest pair and related problems［D］. Storrs， CT： University of Connecticut， 2020： 8-11.

［14］ 张晓滨，杨东山. 基于时间约束的Hausdorff距离的时空轨迹相似度量［J］. 计算机应用研究， 2017， 34（7）：2077-2079. （ZHANG X B， YANG D S. Hausdorff distance about spatial-temporal trajectory similarity based on time restriction［J］. Application Research of Computers， 2017， 34（7）： 2077-2079.）

［15］ 郭岩，罗珞珈，汪洋，等. 一种基于DTW改进的轨迹相似度算法［J］. 国外电子测量技术， 2016， 35（9）： 66-71. （GUO Y， LUO L J， WANG Y， et al. Improved DTW algorithm for trajectory similarity［J］. Foreign Electronic Measurement Technology， 2016， 35（9）： 66-71.）

［16］ 王前东.经典轨迹的相似度量快速算法［J］.系统工程与电子技术，2020，42（10）：2189-2196. （WANG Q D. Fast algorithm of similarity measurement for classical trajectory［J］. Systems Engineering and Electronics， 2020， 42（10）： 2189-2196.）

［17］ 周振宇，郭广礼，贾新果.大地主题解算方法综述［J］.测绘科学，2007，32（4）：190-191，174，200. （ZHOU Z Y， GUO G L， JIA X G. A review on solution of geodetic problem［J］. Science of Surveying and Mapping， 2007， 32（4）： 190-191， 174， 200.）

［18］ EITER T， MANNILA H. Computing discrete Fréchet distance， CD-TR 94/64［R/OL］. ［2022-07-10］.http：//www.kr.tuwien.ac.at/staff/eiter/et-archive/cdtr9464.pdf.

Trajectory prediction of sea targets based on geodetic distance similarity calculation

ZHAO Yijian1，2， LIN Li3， WANG Qianqian1，2，4*， WEN Peng5， YANG Dong5

（1，，100081，；2，（），100081，；332011，100094，；4，314033，；5，100095，）

The existing similarity-based moving target trajectory prediction algorithms are generally classified according to the spatial-temporal characteristics of the data， and the characteristics of the algorithms themselves cannot be reflected. Therefore， a classification method based on algorithm characteristics was proposed. The calculation of the distances between two points is required for the trajectory similarity algorithms to carry out the subsequent calculations， however， the commonly used Euclidean Distance （ED） is only applicable to the problem of moving targets in a small region. A method of similarity calculation using geodetic distance instead of ED was proposed for the trajectory prediction of sea targets moving in a large region. Firstly， the trajectory data were preprocessed and segmented. Then， the discrete Fréchet Distance （FD） was adopted as similarity measure. Finally， synthetic and real data were used to test. Experimental results indicate that when sea targets move in a large region， the ED-based algorithm may gain incorrect prediction results， while the geodetic distance-based algorithm can output correct trajectory prediction.

trajectory similarity; trajectory prediction; Euclidean Distance (ED); geodetic distance; Fréchet Distance (FD)

ZHAO Yijian， born in 1998， M. S. candidate. Her research interests include photoelectronic imaging， data processing.

1001-9081（2023）11-3594-05

10.11772/j.issn.1001-9081.2022101639

2022⁃11⁃02；

2023⁃01⁃06；

赵一鉴（1998—），女，河南洛阳人，硕士研究生，主要研究方向：光电成像、数据处理； 林利（1976—），男，河北沧州人，高级工程师，硕士，主要研究方向：信息通信、航天信息处理； 王茜蒨（1970—），女，江苏徐州人，教授，博士，主要研究方向：光电成像和检测； 闻鹏（1986—），男，陕西汉中人，高级工程师，硕士，主要研究方向：大数据及数据仓库应用； 杨东（1985—），男，山东聊城人，高级工程师，硕士，主要研究方向：人工智能应用。

TP301.6

A

2023⁃01⁃31。

LIN Li， born in 1976， M. S.， senior engineer. His research interests include information communication， aerospace information processing.

WANG Qianqian， born in 1970， Ph. D.， professor. Her research interest include photoelectronic imaging and detection.

WEN Peng， born in 1986， M. S.， senior engineer. His research interest include applications of big data and data warehouse.

YANG Dong， born in 1985， M. S.， senior engineer. His research interest include applications of artificial intelligence.