基于蚁群算法优化反向传播神经网络的软件质量预测

朱嘉豪，郑巍，杨丰玉，樊鑫，肖鹏

基于蚁群算法优化反向传播神经网络的软件质量预测

朱嘉豪1，2*，郑巍1，2，杨丰玉1，2，樊鑫1，2，肖鹏1，2

（1.南昌航空大学 软件学院，南昌 330063； 2.南昌航空大学 软件测评中心，南昌 330063）（ ∗ 通信作者电子邮箱 zhujiahao_nchu@126.com）

针对基于反向传播神经网络（BPNN）的软件质量预测模型存在收敛慢、模型精度不高的问题，提出一种基于蚁群算法优化BPNN的软件质量预测（SQP-ACO-BPNN）方法。首先，选择软件质量评价指标，确立软件质量评价体系；其次，采用BPNN构建初始软件质量预测模型，并利用蚁群优化（ACO）算法确定若干网络结构、网络初始连接权值和阈值；再次，给出网络结构评价函数，选择神经网络模型的最佳结构、网络初始连接权值和阈值；最后，通过BP算法训练该网络，得到最终的软件质量预测模型。在机载嵌入式软件质量预测数据上的实验结果表明，优化后的BPNN模型有效提高了预测的准确率、精确率、召回率和F1值，并且模型能够更快收敛，验证了SQP-ACO-BPNN方法的有效性。

软件质量预测；蚁群优化算法；反向传播神经网络；网络结构评价

0 引言

近年来，软件企业之间的竞争日益激烈，市场环境复杂多变，软件的数量呈指数增长［1-2］，软件的质量越来越难得到保证［3-4］。以对安全性和可靠性要求较高的机载软件为例，因为软件质量问题导致的缺陷和软件失效可能对飞行器产生重大影响，甚至可能造成坠机等重大事故。因此，研究软件质量具有十分重大的意义。软件质量是个复杂又抽象的概念［5-7］，如何客观准确地预测软件质量是软件质量领域的重点课题。随着技术逐渐成熟，神经网络成了构造经验模型的首选方法，它强大的非线性映射能力能有效地拟合软件各方面的特征与软件质量之间的关系。

目前，国内外对基于神经网络的软件质量预测已经有了一些研究，但这些研究都人为地确定网络结构，网络初始连接权值和阈值也都被赋予随机值，存在模型收敛慢、性能不高的问题。在软件质量预测模型中，如何选择最佳的神经网络结构、初始连接权值和阈值成了研究难题。相较于传统优化算法，群体智能算法在没有明确的问题和条件描述、存在多极值问题的情况下均表现出了明显的优势。在群体智能算法中，蚁群优化（Ant Colony Optimization， ACO）算法和粒子群优化（Particle Swarm Optimization， PSO）算法的应用最广泛，其中：ACO算法主要用于离散优化问题的求解，而PSO算法主要用于连续优化问题的求解。在神经网络结构、初始连接权值和阈值的寻优过程中，寻找的是不同参数集合中的离散个体，所以ACO算法在求解问题时具有更大的优势。

基于以上分析，本文提出一种基于ACO算法优化反向传播神经网络的软件质量预测（Software Quality Prediction based on Back Propagation neural network improved by ACO， SQP-ACO-BPNN）方法，基于反向传播神经网络（Back Propagation Neural Network， BPNN），对网络层数、每层网络节点个数、网络初始连接权值以及阈值进行自定义编码，并设计模型评价函数，采用ACO算法寻优，根据评价函数为模型确定最佳的网络结构、初始连接权值和阈值，再利用BP算法训练神经网络，得到收敛更快、性能更好的软件质量预测模型。

1 相关工作

1.1　基于神经网络的软件质量预测

人工神经网络（Artificial Neural Network， ANN）最早由心理学家McCulloch等［8］提出，并构建了一种基于简单逻辑运算的计算机制。Karunanithi等［9］在1992年第一次将ANN技术应用于软件质量预测中，将故障历史作为输入预测未来故障，因为神经网络会自主调整模型复杂度以匹配故障历史数据的复杂度，所以比传统回归模型更准确。1999年，Sitte等［10］根据经验比较了两种不同的软件可靠性预测方法的预测性能：“神经网络”和“参数模型的重新校准”，使用了通用的数据集，研究表明，神经网络不仅使用更加简便，而且能取得更好的结果，进一步证明了神经网络技术在软件质量预测上的有效性。2007年，Su等［11］使用神经网络方法构建动态加权组合模型，在隐藏层中使用了与传统可靠性增长模型不同的激活函数，在真实的软件故障数据集上通过实验验证了模型具有准确的预测能力。2014年，宫丽娜等［12］提出了一种PSO算法优化的BPNN预测软件质量方法，采用PSO算法对BPNN进行优化，有效解决了BPNN出现的收敛速度慢和容易陷入局部最优的问题。2021年，田川等［13］考虑了一种软件质量评价体系，并采用主成分分析方法筛选样本，利用鸽群优化算法改进径向基网络的权值和阈值，改进网络模型逼近精度，提升了模型的收敛速度。但是这些网络结构都是由人工选择，取决于学者对于数据和网络的理解，很难得到网络的最佳结构，网络的初始连接权值和阈值都是初始随机值，容易因为模型结构和初始参数不优导致模型精度不足，通过ACO算法可以有效地解决存在的问题。

1.2　蚁群算法

蚁群在不同的环境下外出觅食，总能寻找到到达食物的最短路径，受此现象的启发，意大利学者Colorni等［14］于1991年提出蚂蚁系统。蚁群的个体之间通过信息素进行交流，通过简单个体组成群体完成复杂的工作，能达到寻找最优解的目的，因此最开始被用来解决旅行商问题，再经过Dorigo和Gambardella等学者改进后被称为蚁群算法。

蚁群算法的应用场景很多，如Li等［15］提出了一种新的蚁群优化算法以解决训练径向基神经网络时出现的连续链接权重问题；Mavrovouniotis等［16］和Abdelbar等［17］通过ACO算法结合梯度下降算法来训练神经网络，解决了网络训练过程中陷入局部最优解的问题；庞清乐等［18］将ACO算法用于确定神经网络上每层网络的节点数以及最优的网络初始连接权值和阈值，但仍存在模型网络层数需要人为确定的问题。

2 SQP‑ACO‑BPNN方法

SQP-ACO-BPNN方法的流程如图1所示，主要分为指标选择、网络结构编码和网络寻优三个部分。

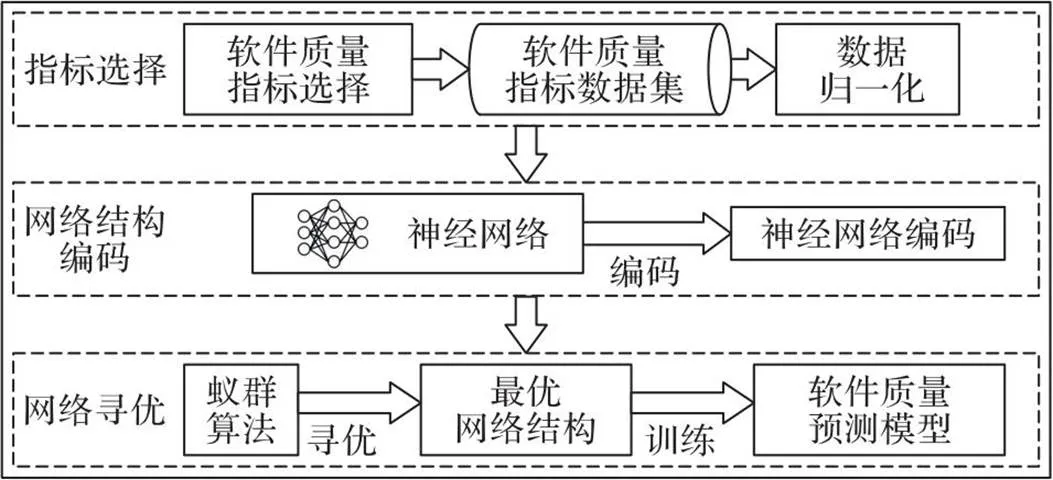
图1　软件质量预测方法流程

2.1　软件质量指标选择

参考ISO/IEC9126软件质量度量标准，可将软件质量特性分为功能性、可靠性、易用性、效率、可维护性和可移植性，根据软件质量特性将软件质量结果划分为优秀、良好、一般和差四种不同类型，由于这些软件质量特性无法直接度量，所以需要利用软件的其他内部属性来间接得到。本文挑选出可以直接度量的软件质量指标如表1所示。将这些软件质量指标作为软件质量预测模型的输入以得到软件质量预测值，从而反映软件质量特性。

表1　软件质量指标

不同评价指标之间的量纲并不相同，数值之间的差距较大，不进行处理容易导致神经网络在训练过程中收敛困难，因此在使用数据前需要将数据进行归一化处理，而归一化方法能够很好地解决此类问题，让不同维度之间的数据在数值上有一定比较性，从而大幅提高分类器的准确性和模型的收敛速度。比较常用的有Min-Max归一化和Z-Score标准化两种方法，Min-Max归一化将原数据映射到［0，1］，不改变原始数据的分布，而Z-Score则将原数据处理成符合正态分布。对于数据较为稳定、不存在极端最大最小值的情况，采用Min-Max归一化方法；当数据存在较多异常值、噪声较多的情况采用Z-Score标准化方法。根据实际数据情况，本文采用Min-Max归一化方法，处理方法如式（1）所示。

其中：min（）为最小值，max（）为最大值。

2.2　网络结构编码

2.2.1BPNN

BPNN的输出结果采用前向传播，误差采用反向传播。以三层神经网络为例，如图2所示，BPNN包含输入层、隐含层和输出层三层结构。当前向传播时，数据从输入层输入，传递给隐含层，经过隐含层处理后再传递给输出层，此时完成一次正向传播过程。当输出结果与真实数据不符时，进入反向传播阶段，误差采用梯度下降的方式从后往前依次修正各层网络连接权值和阈值［19］。

在神经网络正向传播时，上一层的输出直接作为下一层的输入，每层之间都是线性关系，神经网络的拟合能力较弱，为了使得神经网络具备更好的拟合能力，可在网络之间加入激活函数，经过实验研究，通常采用S型（Sigmoid）函数作为激活函数。而在反向传播过程中，损失函数能衡量网络模型的输出与真实标签之间的差距，为模型提供一个优化的目标，对于多分类任务，采用最为广泛的交叉熵函数作为损失函数，函数如式（2）所示。

其中：Tp为目标输出，Dp为实际输出；n为输出层节点数，即软件质量分类数。

2.2.2编码方式

将不同结构的BPNN的网络层数、每层网络的节点数、节点之间相连接的权值和阈值进行拆分。神经网络结构参数ST包含网络层数和每层网络节点数信息，设定网络层数最小为3层，最大为5层，输入层节点数为12（软件质量指标数），输出层节点为4（软件质量类型数，分别为优秀、良好、一般和差），第一隐含层与第三隐含层节点数最大为16，第二隐含层节点数最大为32，所以权值和阈值的最大数量总和为1 348，如表2所示。

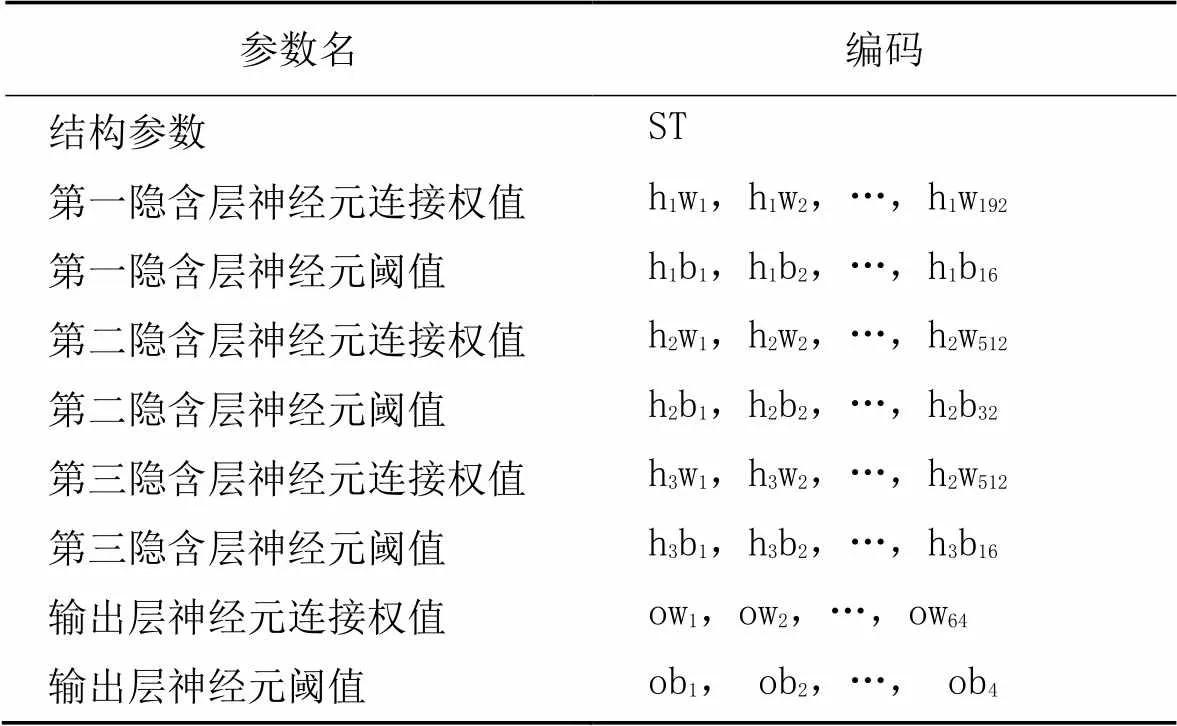
表2　BPNN结构参数

2.3　ACO优化BPNN方法

图3　ACO算法流程

ACO算法具体步骤如下：

步骤3 所有蚂蚁均在每个集合中选择了一个元素，即为找到了食物，根据蚂蚁选择的参数构建神经网络模型，输入训练数据，按式（4）计算交叉熵值，即每只蚂蚁走过的路径长度。

其中：T为目标输出，D为实际输出，为输出层节点数。

步骤4 选择路径最短的只蚂蚁，原路返回巢穴进行信息素更新，蚂蚁所经历的时间为，则按照式（5）更新蚂蚁所选择的信息素浓度。

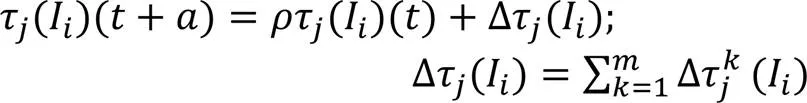
其中：为信息素挥发因子；Δτ（I）表示第只蚂蚁在本轮次中在集合I中第个元素上留下的信息素，计算如式（6）所示。

其中：为常数，用于控制信息素的增长速度；当路径越小时，增长的信息素越多。

步骤5 重复步骤2～4，直至算法中所有蚂蚁收敛到同一路径或者达到最大循环次数停止。

3 实验与结果分析

3.1　评价指标

为了从ACO算法中得到最优的网络结构，需要定义评价函数对网络结构进行评价，因为模型层数越多、节点越多，模型越复杂，在模型训练后越容易拟合数据，所以建立评价函数如式（7）所示。

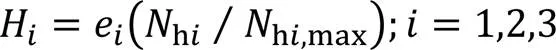
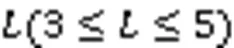
为了更全面地评价本文SQP-ACO-BPNN方法的性能，选用准确率（Accuracy）、精确率（Precision）、召回率（Recall）和F1值对模型进行评价，并使用ACO算法对在多分类任务上效果较好的支持向量机和加权朴素贝叶斯模型进行优化，分别对比ACO算法优化后的BPNN模型、未优化过的BPNN模型、ACO算法优化支持向量机模型（Ant Colony Optimization improved Support Vector Machine， ACO-SVM）和ACO算法优化加权朴素贝叶斯（Ant Colony Optimization improved Weighted Naive Bayes， ACO-WNB）模型的性能。

3.2　实验结果

根据研究经验设置神经网络结构参数h1，max=16，h2，max=32，h3，max=16，学习率为0.01，最大迭代次数为700。设置网络结构评价函数参数，常数=1.0，第一隐含层影响系数1=1.5，第二隐含层影响系数2=1.3，第三隐含层影响系数3=1.0。

3.2.1ACO算法超参数选取

为了得到更好的实验效果，首先根据经验设置初始信息素=1.0，信息素常量=10，再通过实验对ACO算法的蚂蚁数量，信息素挥发因子，信息启发式因子，期望启发式因子以及最大迭代次数max等超参数进行选择。分别进行多次实验，当相邻两次迭代中的最优解的差值小于0.001则停止迭代。

在研究蚂蚁数量对ACO算法的影响过程中，其他超参数选择为：信息素挥发因子=0.5，信息启发式因子=1.0，期望启发式因子=2.0。结果如表3所示，可知蚂蚁数量增大后，搜索的随机性得到了增强，但是收敛减慢，在蚂蚁数量增长到50以后，最优路径长度并无明显变化，但是迭代次数增多，所以蚂蚁数量选择为50较为合理。

在研究信息素挥发因子对ACO算法的影响时，设置蚂蚁数量=50，信息启发式因子=1.0，期望启发式因子=2.0。结果如表4所示，不难看出，当信息素挥发因子较小时，算法搜索的随机性减弱，算法收敛很快，但是容易陷入局部最优，综合考虑算法的全局搜索能力和收敛速度两项指标，选择信息素挥发因子=0.5较为合理。

最后研究启发式因子对ACO算法的影响，设置蚂蚁数量=50，信息素挥发因子=0.5。结果如表5所示，适当选择和的取值，使得ACO算法能得到较好的搜索结果和较少的迭代次数，通过实验结果可知选择=1.0，=2.0较好。

综上所述，根据实验结果可知，选取蚂蚁数量=50，信息素挥发因子=0.5，信息启发式因子=1.0，期望启发式因子=2.0，最大迭代次数max=50，初始信息素=1.0，信息素常量=10使ACO算法能得到较好的实验结果。

表5　启发式因子对ACO的影响

3.2.2网络结构

为了选出最好的网络结构模型，分别进行了50次实验，选出最好的10个网络模型，实验结果如表6所示。根据评价函数值可知，最好的神经网络结构为（12，15，10，4），即4层神经网络，输入层神经元节点数量为12，第一隐含层神经元数量为15，第二隐含层神经元节点数量为10，输出层神经元节点数量为4。

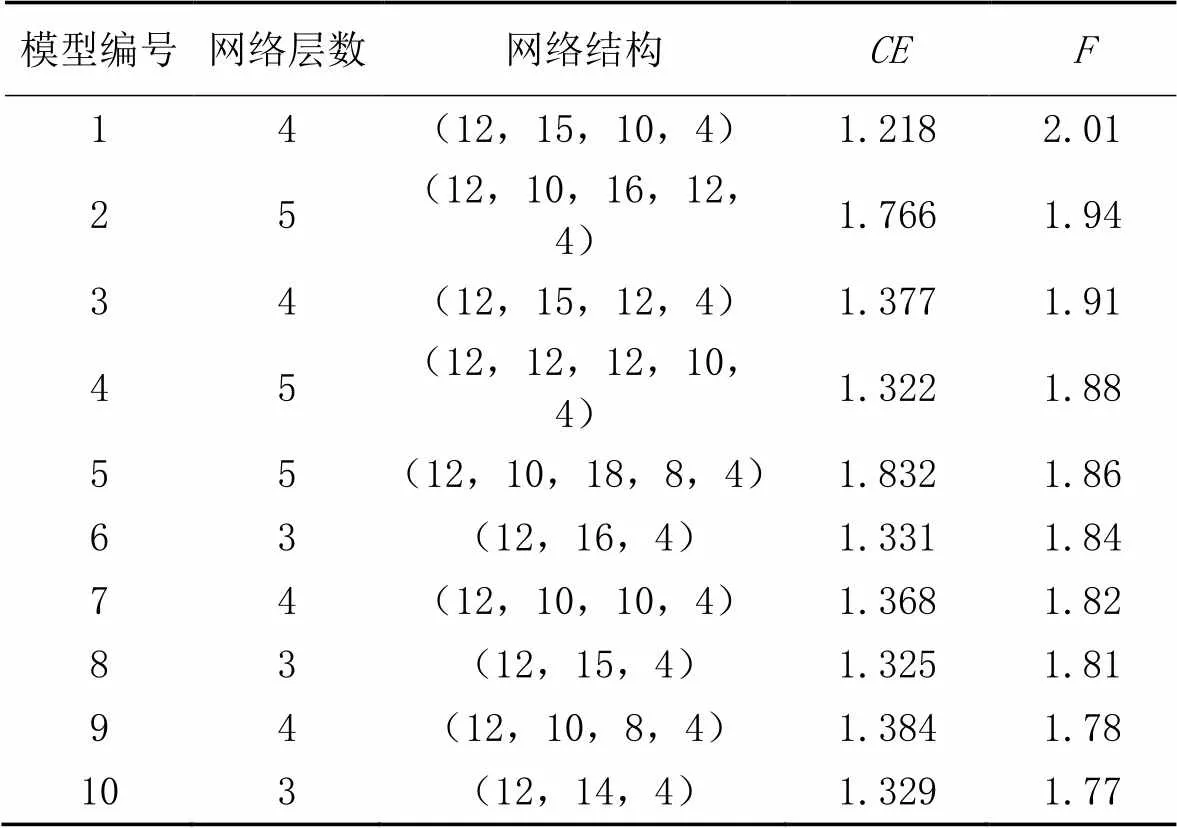
表6　网络模型结构结果

3.2.3收敛效果

将选出的最优结构BPNN模型（12，15，10，4）与基础BPNN模型（12，16，32，16，4）分别进行模型训练，训练过程如图4所示，可见，经过ACO算法优化的BPNN结构模型比基础BPNN模型能够更快收敛，并且误差更小。

图4　模型训练过程

3.2.4实验精度

为了检验本文方法的实际效果，采用机载嵌入式软件质量预测数据集进行实验，将软件质量类别分为四类（优、良、一般和差），在测试某类别的预测效果时，将该类别当作正类，其他类别当作负类，数据按照7∶3随机分为训练集和测试集。

分别训练SQP-ACO-BPNN、未优化的BPNN、ACO-SVM和ACO-WNB。在SVM中，选择径向基函数作为核函数，通过ACO算法对正则化系数和径向基函数带宽进行寻优，根据模型准确率来更新信息素，不断优化正则化系数和径向基函数带宽。在WNB中，权重的选择直接关系到分类的效果，为了提高分类的准确性，同样引入ACO算法根据模型准确率来更新信息素，对特征权值进行迭代和全局寻优，获得最优权值。在ACO算法优化BPNN过程中，利用ACO算法对网络结构、初始连接权值和阈值进行寻优，选用交叉熵函数作为个体适应度函数，通过计算交叉熵值来更新信息素，相较于ACO-SVM和ACO-WNB，采用交叉熵值作为个体适应度值比采用模型准确率更精确、更苛刻。ACO-SVM只对正则化系数和径向基函数带宽两个参数进行优化，ACO-WNB同样只优化了特征权值，依然存在太多的不可控性，而SQP-ACO-BPNN不仅优化了网络层数、每层网络节点数量，还对网络初始连接权值和阈值进行了优化，设计了适合ACO算法寻优的网络编码方式，本文中的ACO算法与传统ACO算法不同，根据网络的前向传播特性设计了专用于神经网络寻优的适应度函数，并且在每个轮次中，只选择部分效果较好的蚂蚁更新路径上的信息素浓度，提高了ACO算法的收敛速度。SQP-ACO-BPNN比ACO-SVM和ACO-WNB在ACO算法优化过程中优化的可控参数更多，优化过程更严谨，个体适应度函数选用更好。

实验结果如图5（a）～（d）所示。可以看出，经过ACO算法优化后的BPNN结构、初始连接权值和阈值后的SQP-ACO-BPNN相较于未优化的BPNN在准确率、精确率、召回率和F1值上均取得了较大的提升。未优化的BPNN在四种分类上预测的平均准确率、精确率、召回率和F1值分别为89.9%、91.6%、91.3%和91.4%，经过ACO算法优化后的SQP-ACO-BPNN预测的平均准确率、精确率、召回率和F1值分别为95.2%、95.4%、95.1%和95.7%。在准确率、精确率、召回率和F1值上分别提高了5.3、3.8、3.8和4.3个百分点。同样由图5可知，SQP-ACO-BPNN相较于ACO-SVM和ACO-WNB同样具有更高的准确率、精确率、召回率和F1值。

综上所述，采用ACO算法优化网络结构、初始连接权值和阈值后，对于软件质量预测性能具有一定的提升。

图5　不同方法的性能对比

4 结语

针对传统基于神经网络的软件质量预测方法的不足，本文提出了一种基于ACO优化BPNN的软件质量预测方法。考虑到不同指标数据量纲不同对模型训练的影响，为解决此问题，对数据进行归一化，按照7∶3分为训练集和测试集；考虑到神经网络结构、网络初始连接权值和阈值对训练后模型性能的影响，将网络结构（包括网络层数和每层网络节点数）、网络初始连接权值和阈值进行编码，采用ACO算法对网络进行寻优，选择出最佳的网络结构、网络初始连接权值和阈值，解决了网络结构不确定、网络初始连接权值和阈值不稳定导致模型收敛慢、性能不高的问题。在机载嵌入式软件质量预测数据集上的实验结果表明，SQP-ACO-BPNN比未优化的BPNN在训练过程中能够更快收敛，并且比未优化的BPNN、ACO-SVM和ACO-WNB在测试集上具有更高的准确率、精确率、召回率和F1值。

目前的实验中仍然根据经验设置激活函数和学习率，可能存在特殊场景下不适用的情况，后续研究将考虑如何优化选择激活函数和学习率等参数。

[1] RODRIGUEZ M， PIATTINI M， EBERT C. Software verification and validation technologies and tools［J］. IEEE Software， 2019， 36（2）： 13-24.

[2] KLOTINS E， UNTERKALMSTEINER M， GORSCHEK T. Software engineering antipatterns in start-ups［J］. IEEE Software， 2018， 36（2）： 118-126.

[3] RAJAPAKSHA D， TANTITHAMTHAVORN C， JIARPAKDEE J， et al. SQAPlanner： Generating data-informed software quality improvement plans［J］. IEEE Transactions on Software Engineering， 2021， 48（8）： 2814-2835.

[4] BOGNER J， FRITZSCH J， WAGNER S， et al. Microservices in industry： insights into technologies， characteristics， and software quality［C］// Proceedings of the 2019 IEEE International Conference on Software Architecture Companion. Piscataway： IEEE， 2019： 187-195.

[5] LIU Y， KHOSHGOFTAAR T M， SELIYA N. Evolutionary optimization of software quality modeling with multiple repositories［J］. IEEE Transactions on Software Engineering， 2010， 36（6）： 852-864.

[6] ZHOU Z Q， XIANG S， CHEN T Y. Metamorphic testing for software quality assessment： a study of search engines［J］. IEEE Transactions on Software Engineering， 2015， 42（3）： 264-284.

[7] AZUMA M. Software products evaluation system： quality models， metrics and processes — International Standards and Japanese practice［J］. Information and Software Technology， 1996， 38（3）： 145-154.

[8] McCULLOCH W S， PITTS W. A logical calculus of the ideas immanent in nervous activity［J］. The Bulletin of Mathematical Biophysics， 1943， 5（4）： 115-133.

[9] KARUNANITHI N， WHITLEY D， MALAIYA Y K. Using neural networks in reliability prediction［J］. IEEE Software， 1992， 9（4）： 53-59.

[10] SITTE R. Comparison of software-reliability-growth predictions： neural networks vs parametric-recalibration［J］. IEEE Transactions on Reliability， 1999， 48（3）： 285-291.

[11] SU Y S， HUANG C Y. Neural-network-based approaches for software reliability estimation using dynamic weighted combinational models［J］. Journal of Systems and Software， 2007， 80（4）： 606-615.

[12] 宫丽娜，马怀志.粒子群算法优化的BP网络预测软件质量［J］.计算机工程与应用，2014，50（23）：65-68.（GONG L N，MA H Z. Software quality prediction of BP network based on PSO ［J］. Computer Engineering and Applications， 2014，50（23）：65-68.）

[13] 田川，王闯，刘灿，等.基于鸽群改进RBF网络的软件质量预测方法［J］.航空计算技术，2021，51（5）：24-28.（TIAN C， WANG C， LIU C，et al. Software quality prediction based on PIO-RBF ［J］. Aeronautical Computing Technique， 2021，51（5）：24-28.）

[14] COLORNI A， DORIGO M， MANIEZZO V. Distributed optimization by ant colonies［C］// Proceedings of the 1st European Conference on Artificial Life. Cambridge， MA： MIT Press， 1991： 134-142.

[15] LI J， LIU X， JIANG H， et al. Melt index prediction by adaptively aggregated RBF neural networks trained with novel ACO algorithm［J］. Journal of Applied Polymer Science， 2012， 125（2）： 943-951.

[16] MAVROVOUNIOTIS M， YANG S. Training neural networks with ant colony optimization algorithms for pattern classification ［J］. Soft Computing， 2015， 19（6）： 1511-1522.

[17] ABDELBAR A M， SALAMA K M. A gradient-guided ACO algorithm for neural network learning［C］// Proceedings of the 2015 IEEE Symposium Series on Computational Intelligence. Piscataway： IEEE， 2015： 1133-1140.

[18] 庞清乐，刘新允.基于蚁群神经网络的财务危机预警方法［J］.数理统计与管理，2011，30（3）：554-561.（PANG Q L，LIU X Y. Ant colony algorithms and neural network based early-warning system for enterprise financial distress ［J］. Journal of Applied Statistics and Management， 2011， 30（3）：554-561.）

[19] 王李进，吴保国，郑德祥.基于人工神经网络的软件质量评价［J］.计算机应用与软件，2008，25（12）：133-134，150.（WANG L J，WU B G，ZHENG D X. Software quality evaluation based on artificial neural network［J］. Computer Applications and Software， 2008， 25（12）： 133-134， 150.）

Software quality prediction based on back propagation neural network optimized by ant colony optimization algorithm

ZHU Jiahao1，2*， ZHENG Wei1，2， YANG Fengyu1，2， FAN Xin1，2， XIAO Peng1，2

（1，，330063，；2，，330063，）

Concerning the problems of slow convergence and low accuracy of software quality prediction model based on Back Propagation Neural Network （BPNN）， a Software Quality Prediction method based on BPNN optimized by Ant Colony Optimization algorithm （SQP-ACO-BPNN） was proposed. Firstly， the software quality evaluation factors were selected and a software quality evaluation system was determined. Secondly， BPNN was adopted to build initial software quality prediction model and ACO algorithm was used to determine network structures， initial connection weights and thresholds of network. Then， an evaluation function was given to select the best structure， initial connection weights and thresholds of the network. Finally， the network was trained by BP algorithm， and the final software quality prediction model was obtained. Experimental results of predicting the quality of airborne embedded software show that the accuracy， precision， recall and F1 value of the optimized BPNN model are all improved with faster convergence， which indicates the validity of SQP-ACO-BPNN.

software quality prediction; Ant Colony Optimization (ACO) algorithm; Back Propagation Neural Network (BPNN); network structure evaluation

1001-9081（2023）11-3568-06

10.11772/j.issn.1001-9081.2022101600

2022⁃10⁃25；

2022⁃12⁃17；

总装预研基金项目（JZX7J202202ZL002000）。

朱嘉豪（1998—），男，江西丰城人，硕士研究生，CCF会员，主要研究方向：软件可靠性、软件质量预测； 郑巍（1982—），男，江西萍乡人，教授，博士，CCF会员，主要研究方向：复杂网络、软件可靠性； 杨丰玉（1980—），男，江西九江人，副教授，硕士，CCF会员，主要研究方向：大数据分析； 樊鑫（1981—），男，湖北荆州人，副教授，硕士，CCF会员，主要研究方向：软件测试； 肖鹏（1988—），男，江西吉安人，讲师，博士，CCF会员，主要研究方向：软件测试。

TP311.5； TP18

A

2022⁃12⁃26。

This work is partially supported by Assemble Pre-Research Foundation of China （JZX7J202202ZL002000）.

ZHU Jiahao， born in 1998， M.S. candidate. His research interests include software reliability， software quality prediction.

ZHENG Wei， born in 1982， Ph.D.， professor. His research interests include complex network， software reliability.

YANG Fengyu， born in 1980， M.S.， associate professor. His research interests include big data analysis.

FAN Xin， born in 1981， M.S.， associate professor. His research interests include software testing.

XIAO Peng， born in 1988， Ph.D.， lecturer. His research interests include software testing.