基于多领导者Stackelberg博弈的分层联邦学习激励机制设计

耿方兴，李卓*，陈昕

基于多领导者Stackelberg博弈的分层联邦学习激励机制设计

耿方兴1，2，李卓1，2*，陈昕2

（1.网络文化与数字传播北京市重点实验室（北京信息科技大学），北京 100101； 2.北京信息科技大学 计算机学院，北京 100101）（ ∗ 通信作者电子邮箱lizhuo@bistu.edu.cn）

分层联邦学习中隐私安全与资源消耗等问题的存在降低了参与者的积极性。为鼓励足够多的参与者积极参与学习任务，并针对多移动设备与多边缘服务器之间的决策问题，提出基于多领导者Stackelberg博弈的激励机制。首先，通过量化移动设备的成本效用与边缘服务器的支付报酬，构建效用函数并定义最优化问题；其次，将移动设备之间的交互建模为演化博弈，将边缘服务器之间的交互建模为非合作博弈。为求解最优边缘服务器选择和定价策略，提出多轮迭代边缘服务器选择算法（MIES）和梯度迭代定价算法（GIPA），前者用于求解移动设备之间的演化博弈均衡解，后者用于求解边缘服务器之间的定价竞争问题。实验结果表明，所提算法GIPA与最优定价预测策略（OPPS）、历史最优定价策略（HOPS）和随机定价策略（RPS）相比，可使边缘服务器的平均效用分别提高4.06%、10.08%和31.39%。

分层联邦学习；激励机制；定价策略；多领导者Stackelberg博弈；演化博弈

0 引言

随着移动设备的普及和网络程序的广泛应用，私人数据量呈爆炸式增长。得益于服务器计算能力与存储容量的提升，大数据驱动的机器学习方法能够实现大规模的集中式训练，该方法通过大量移动设备将本地数据上传至云服务器，完成全局模型的训练。然而，移动设备所产生的本地数据中通常包含重要的私人信息，一旦此类数据泄露［1］或被用于预期以外的目的，用户隐私将受到损害。鉴于上述存在的数据安全隐患，用户不愿将私人数据共享至云服务器。为解决集中式训练存在的数据安全问题，联邦学习［2］应运而生。联邦学习的分布式设计使得所有的训练数据保存在设备本地，移动设备基于模型所有者发布的模型，在本地完成参数更新，实现模型的协同训练。

为达到预期的模型精度，联邦学习中的大量模型参数需要通过复杂的网络环境进行多轮次的数据传输，因此移动设备面临着网络拥塞和通信故障的问题。针对上述问题，研究人员提出分层联邦学习框架［3］，其中移动设备不直接将本地模型上传至云端而是上传至边缘服务器。边缘服务器作为中转站，聚合移动设备的模型参数，并上传至云端实现全局模型的聚合。

在分层联邦学习过程中，当移动设备参与学习任务时，不可避免地会消耗设备资源，包括计算、通信资源等。因此移动设备无偿地贡献资源是不切实际的；同时分层联邦学习框架仍然面临各种安全风险，如恶意节点可以通过中间梯度推断训练数据的重要信息、边缘服务器也可通过生成的对抗网络学习客户训练数据的私人信息［4］。由于这些风险与参与分层联邦学习任务成本的增加，如果没有足够的补偿，移动设备可能不愿意参与并上传训练后的模型参数。因此，为促进分层联邦学习的持续发展需要设计有效的激励机制。

目前基于分层联邦学习的激励机制研究中存在的问题主要包括：

1）现有的部分联邦学习研究中，参与者是完全理性的［5-7］，但这种假设并不符合实际，因为移动设备的地理位置与网络拥塞情况都会影响参与者获取信息的速度和信息完整性。同时由于边缘服务器给予的报酬有限，使得移动设备之间存在竞争关系。因此如何建立设备之间的博弈模型，求解出移动设备的最优选择策略是当前存在的问题。

2）移动设备通过贡献自身的数据和计算资源获得报酬，同时边缘服务器也可通过购买移动设备的资源训练出高质量的模型，获得更高的收益。而移动设备提供的资源有限，因此边缘服务器之间存在竞争关系，如何建立一个合理的博弈模型，求解各方都满意的定价策略，也是当前存在的问题。

针对上述问题，本文将移动设备之间的交互构建为演化博弈，同时将多边缘服务器之间的竞争构建为非合作博弈，并证明了移动设备之间的博弈纳什均衡的存在性；提出了基于多领导者Stackelberg博弈的激励机制，该机制通过调整移动设备和边缘服务器的策略，解决了效用的最优化问题；通过实验分析，验证了基于多领导者Stackelberg博弈激励机制的可行性，并通过对比历史最优定价策略（Historical Optimal Pricing Strategy， HOPS）、最优定价预测策略（Optimal Pricing Prediction Strategy， OPPS）和随机定价策略验证了该机制的有效性。

1 相关工作

基于演化博弈激励机制设计的现有工作中，文献［8］中将企业和领先用户作为博弈主体，构建演化博弈模型，并探究领先用户的知识共享激励机制问题；文献［9］中提出了一个基于演化博弈理论的动态激励模型，对用户在数据共享中的博弈过程进行建模，并分析了模型策略的稳定性；文献［10］中为具有有限理性的移动设备构建了演化博弈模型，以调整它们的训练策略，从而最大化设备的个体效用；文献［11］中将异构网络中的用户接入问题建模为演化博弈问题，并基于强化学习设计了低复杂度自组织用户接入算法，实现了用户的公平性；为了实现高效的分层联邦学习，在非合作参与方（即移动设备、边缘服务器和云服务器）的背景下，文献［12］为解决边缘关联和资源分配问题，将分层联邦学习分为两层，采取演化博弈模拟移动设备的选择过程，并通过性能评估验证了演化博弈的唯一性和稳定性。但上述方法主要针对移动设备之间的交互与策略变换，并集中解决移动设备所产生的问题，未考虑边缘服务器作为分层联邦学习中的参与方对系统模型的影响。

在基于Stackelberg博弈激励机制设计的现有工作中，文献［13］中构建了Stackelberg博弈模型以研究移动设备之间以及移动设备与模型所有者之间的交互作用，在该模型中，移动设备能够提供中继服务，并收取一定报酬。此外，对于联邦学习中服务器与移动设备之间的交互也可采用Stackelberg博弈，如文献［14］中采用两个阶段的Stackelberg博弈模型，同时设计了激励机制，该机制不仅激励移动设备尽最大努力训练联邦学习模型，也保证服务器达到最优效用。文献［15］中采用Stackelberg博弈对云服务器和参与联邦学习的设备之间基于激励的交互进行建模，以激励设备参与联邦学习。除此之外，文献［16］中研究了群体感知服务提供商的最优激励机制，提出了两阶段Stackelberg博弈，分析了移动用户的参与水平，同时采用反向归纳法分析了群体感知服务提供商的最优激励机制。类似地，文献［17］中设计了多领导者多追随者的两层Stackelberg博弈模型，并构建了一种分布式机制以分析移动边缘计算支持的边缘云系统中服务商与移动设备之间的交互。该模型证明了Stackelberg均衡的存在性，同时提出了一种分布式算法，即迭代的Stackelberg博弈定价算法。实验结果表明，与其他传统的任务卸载方案相比，该算法能显著降低物联网移动设备的负效用；然而，该算法主要针对计算卸载，对于移动设备之间的博弈，它未考虑到移动设备之间存在信息不对称的问题，因此该算法并不适用于信息不完全的场景。针对上述相关模型的不足，本文构建了演化博弈模型与非合作博弈模型，并基于多领导者Stackelberg博弈设计激励机制，在资源有限的条件下探究了移动设备策略的动态性，并优化了移动设备和边缘服务器的效用。

2 系统模型与问题定义

2.1　分层联邦学习框架

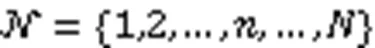
1）本地更新。移动设备能够接收来自边缘服务器的全局模型，并基于本地数据进行模型训练，同时该过程会消耗移动设备的部分资源。最终移动设备将训练完成的模型参数上传至边缘服务器，并获得边缘服务器给予的报酬。

2）边缘服务器端聚合。边缘服务器对接收的模型的参数进行聚合，并将聚合后的模型参数上传至云服务器，并获得模型拥有者给予的报酬。

3）云端聚合。云服务器进行全局模型参数聚合，并将更新完成的模型参数发送给边缘服务器，再由边缘服务器发送给移动设备。

上述三个步骤将会持续迭代进行，直到全局模型收敛或达到最大迭代次数。

2.2　移动设备与边缘服务器的效用模型

图1　分层联邦学习框架

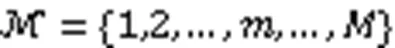
在种群的移动设备会因选择边缘服务器进行模型训练而产生一定的成本，即计算成本与通信成本。在不同种群中，移动设备之间的数据量存在一定差异，因此计算成本随之变动。随着数据量的增多，移动设备的计算成本也会增加［13］。在时刻的计算成本定义如下：

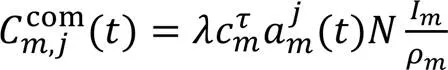
为激励移动设备积极参与分层联邦学习，边缘服务器根据种群中的移动设备的数据贡献占比与平均数据贡献作比较，模型训练的数据量越大，则获得的报酬越多。在经过次迭代后，报酬定义如下：

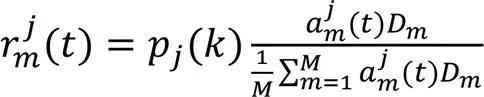
由上述的移动设备的通信与计算模型可得，种群中移动设备因选择边缘服务器所产生的总成本为：

由式（3）与式（4）可得，定义种群中选择边缘服务器的移动设备总效用为：

同时可得种群的总效用为：

通过将接收到的局部模型聚合后，边缘服务器会根据模型的质量获得一定的收益。由于具有更大数据覆盖率的边缘服务器被认为对分层联邦学习模型具有更高价值，因为模型性能可得到更大提升，如模型精度［18］。因此定义边缘服务器的收益如下：

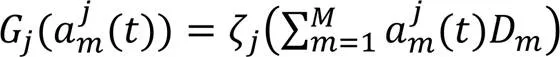
2.3　问题定义

针对上述移动设备和边缘服务器的效应函数分析，对于边缘服务器的定价策略，种群中的移动设备动态变换选择边缘服务器的策略，以最大化自身效用，即：

3 多领导者Stackelberg博弈模型构建

本文将移动设备与边缘服务器之间的交互建模为多领导者Stackelberg博弈模型，如图2所示。该博弈由移动设备之间的演化博弈与边缘服务器之间的非合作博弈构成。随着博弈的进行，二者不断调整策略，以实现效用最大化。

图2　多领导者Stackelberg博弈模型

3.1　移动设备之间的演化博弈均衡分析

与传统博弈中的参与者立即获得最优解的方式不同，演化博弈中的参与者逐渐调整他们的策略并最终达到均衡解［20-21］。同时，演化博弈可以捕捉参与者策略适应过程中的动态和趋势，因此能够很好地刻画分层联邦学习中移动设备之间的动态交互与有限理性。

根据边缘服务器决定的定价，移动设备通过改变选择服务器的策略相互竞争，以最大化自身利益。将移动设备之间的演化博弈定义为：

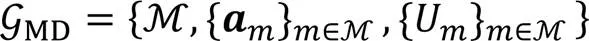
演化博弈过程中，种群的移动设备不断地变换策略以寻求最优的效用值。因此，定义时刻时，种群的平均效用为：

结合上述效用分析，同时为捕捉有限理性的移动设备动态调整策略的过程，引入复制动态方程，定义如下：

3.2　边缘服务器之间的非合作博弈均衡分析

作为领导者的边缘服务器并不能在当前轮次获得所有定价信息，只能根据移动设备的选择策略动态地调整定价。同时由于资源的有限性，边缘服务器之间存在着竞争关系。

在分层联邦学习中，每个边缘服务器都被认为是自私的，同时它们之间没有合作或协定［23］。由于非合作博弈描述了自利参与者之间的冲突关系，因此在有限预算下，边缘服务器之间的激励问题可被建模为非合作博弈［24］。将非合作博弈定义为：

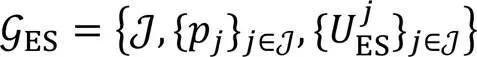
下面将对边缘服务器之间博弈的均衡解进行分析。

由式（10）与式（19）将优化问题改写为：

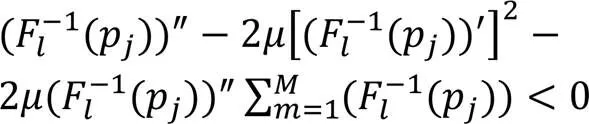
综上所述，通过证明移动设备之间的演化博弈和边缘服务器之间的非合作博弈存在纳什均衡，从而证明多领导者Stackelberg博弈均衡的存在性。

4 基于多领导者Stackelberg博弈的激励机制设计

本文通过求解演化博弈与非合作博弈均衡解的算法，进而求得多领导者Stackelberg博弈均衡解。在每一轮定价更新中，通过自身效用与平均效用的比较，移动设备不断更新选择边缘服务器的策略，最终达到演化博弈的纳什均衡。根据上一轮其他边缘服务器的定价策略，边缘服务器更新自身定价，并开始下一轮的定价更新。

4.1　边缘服务器选择算法设计

算法1 多轮迭代边缘服务器选择算法（MIES）。

6） end for

9） 移动设备变换选择策略，以获得更高效用

10） end if

11） end for

12） end for

15） end for

4.2　边缘服务器的定价算法设计

算法2 梯度迭代定价算法（GIPA）。

7） end for

10） end while

5 实验与结果分析

表1　模拟参数设置

5.1　MIES算法分析

本节通过实验分析种群占比的变化趋势，并讨论MIES对移动设备效用的影响。

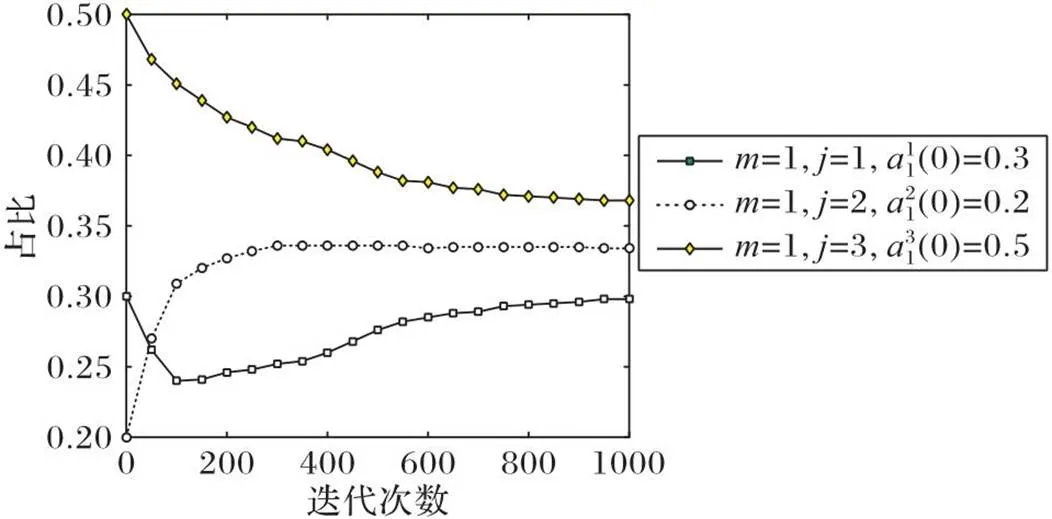
图3　随迭代次数的变化趋势（）

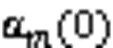
图5显示的是在边缘服务器定价不变的情况下，不同种群中移动设备总效用的对比。从图5中可以看到，在初始情况下，种群2的总效用最高，但随着迭代次数的增加总效用逐渐下降。根据MIES算法，为追求自身效用最大化，移动设备的策略逐渐趋向于最优解，因此种群2的策略不再占优。同时由于种群中数据量的不同，获得的收益趋于不同的稳定值。

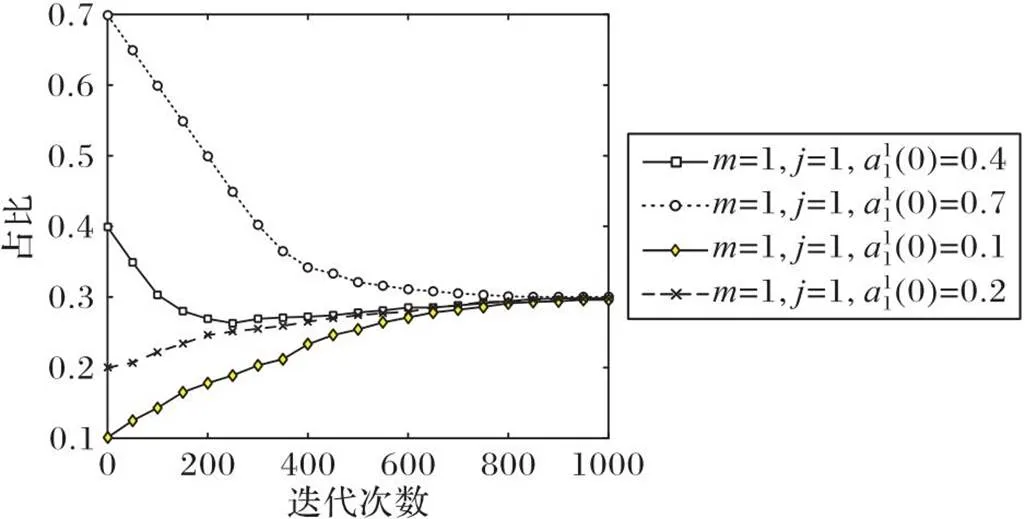
图4　不同初始状态下随迭代次数的变化趋势（）

图5　边缘服务器定价不变时不同种群中移动设备总效用的对比

5.2　GIPA分析

本节通过实验分析边缘服务器定价的变化趋势，并讨论GIPA对边缘服务器效用的影响。

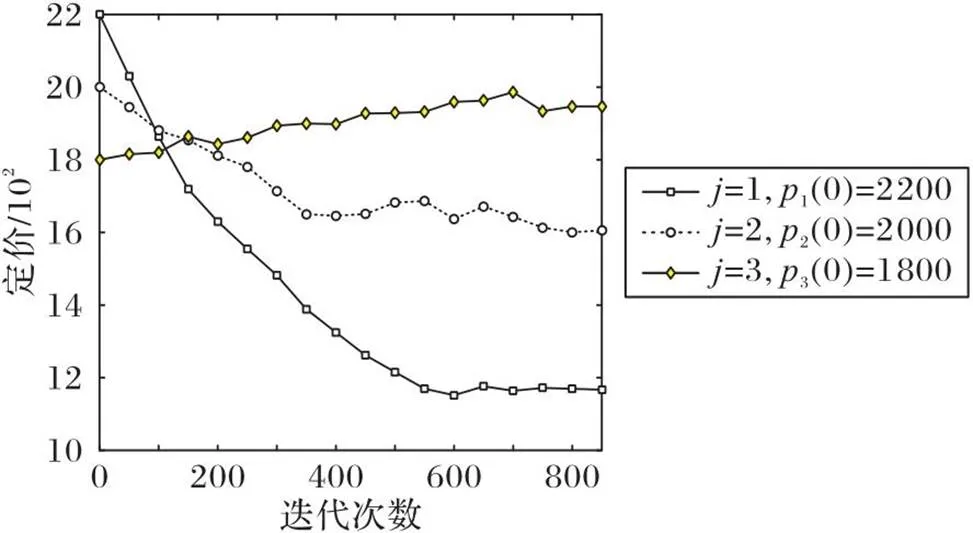
图6　有限次迭代后边缘服务器的定价趋势

边缘服务器购买移动设备的资源，确定资源的价格，并通过聚合移动设备的训练模型获得收益。针对服务器的定价，比较了以下四种定价策略：

1）随机定价策略（Random Pricing Strategy， RPS）：在最大与最小定价区间内，边缘服务随机确定资源定价。

2）历史最优定价策略（HOPS）［26］：根据历史最优定价策略，边缘服务器将它作为当前资源定价策略。

3）最优定价预测策略（OPPS）［27］：采用指数遗忘函数分配权重，对距离当前最近的定价的历史记录赋予更大的权重，并对过时的定价记录赋予更小的权重，根据权重分配获得当前的定价策略。

4）梯度迭代定价算法（GIPA）：根据移动设备之间的演化博弈结果，服务器持续更新价格，直到给出最优资源定价策略。

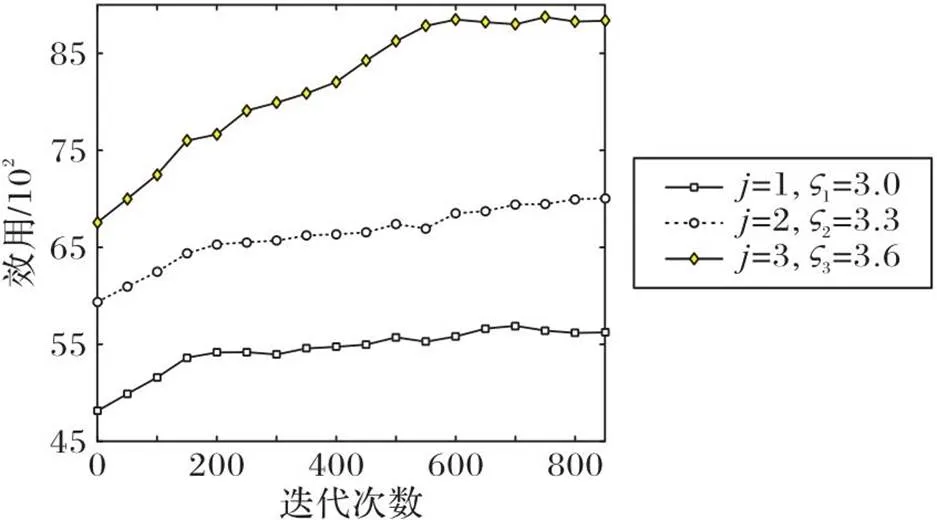
图7　不同收益参数下的边缘服务器效用

图8给出了上述四种不同的定价策略下边缘服务器的效用对比。实验结果表明，在相同的实验条件下，GIPA与OPPS、HOPS和RPS相比，边缘服务器的平均效用分别提高了4.06%、10.08%和31.39%。这是由于GIPA能够找到最适合当前移动设备的资源定价，并在与移动设备的博弈过程中获得最大效用。

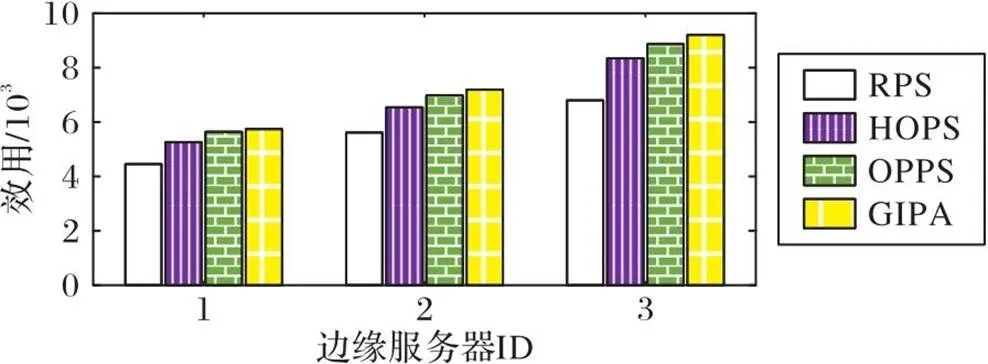
图8　不同的定价策略下的边缘服务器的效用对比

上述实验结果验证了GIPA能够实现边缘服务器的效用最大化。节点获得的报酬能够以某种方式影响设备的决策。在不同报酬的激励机制下，设备将执行不同的训练策略，从而影响最终的分层联邦学习模型性能［28］。因此，为探究多领导者Stackelberg博弈激励机制对设备提供高质量模型影响，定义边缘服务器训练模型的积极程度为：

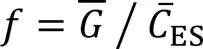
如图9所示，随着参与到分层联邦学习中的移动设备数量增多，边缘服务器的积极程度也随之变化。由图9可知，积极程度变化的幅度较为平缓，这是由于在移动设备为边缘服务器提供更多数据的同时，也会产生相应的资源消耗。同时，与OPPS、HOPS和RPS定价策略相比，GIPA策略下的边缘服务器能获得更高的收益并且更积极地提高模型质量。

图9　不同定价策略下模型的积极程度对比

6 结语

针对移动设备与边缘服务器的最优化问题，本文将移动设备与边缘服务器之间的交互建模为多领导者Stackelberg博弈，该博弈由移动设备之间的演化博弈与边缘服务器之间的非合作博弈构成；还设计了MIES和GIPA分别求解演化博弈的均衡解和边缘服务器之间非合作博弈的均衡解，进而得到最优的边缘服务器选择和定价策略。实验结果表明所提算法GIPA与OPPS、HOPS和RPS相比，边缘服务器的平均效用分别提高了4.06%、10.08%和31.39%。本文探究了移动设备与边缘服务器之间的博弈，但并未考虑云服务器与它们之间的博弈，在未来的工作中，可从三者相互博弈的角度出发，设计更有效的激励机制。

[1] 谭作文，张连福. 机器学习隐私保护研究综述［J］. 软件学报， 2020， 31（7）：2127-2156.（TAN Z W， ZHANG L F. Survey on privacy preserving techniques for machine learning［J］. Journal of Software， 2020， 31（7）： 2127-2156.）

[2] McMAHAN H B， MOORE E， RAMAGE D， et al. Communication-efficient learning of deep networks from decentralized data［C］// Proceedings of the 20th International Conference on Artificial Intelligence and Statistics. New York： JMLR.org， 2017：1273-1282.

[3] ABAD M S H， OZFATURA E， GÜNDÜZ D， et al. Hierarchical federated learning across heterogeneous cellular networks［C］// Proceedings of the 2020 IEEE International Conference on Acoustics， Speech and Signal Processing. Piscataway： IEEE， 2020： 8866-8870.

[4] TU X， ZHU K， LUONG N C， et al. Incentive mechanisms for federated learning： from economic and game theoretic perspective［J］. IEEE Transactions on Cognitive Communications and Networking， 2022， 8（3）： 1566-1593.

[5] TIAN M， CHEN Y， LIU Y， et al. A contract theory based incentive mechanism for federated learning［EB/OL］. （2021-08-12） ［2022-08-10］.https：//arxiv.org/pdf/2108.05568.pdf.

[6] YU H， LIU Z， LIU Y， et al. A fairness-aware incentive scheme for federated learning［C］// Proceedings of the 2020 AAAI/ACM Conference on AI， Ethics， and Society. New York： ACM， 2020： 393-399.

[7] ZENG R， ZHANG S， WANG J， et al. FMore： an incentive scheme of multi-dimensional auction for federated learning in MEC［C］// Proceedings of the IEEE 40th International Conference on Distributed Computing Systems. Piscataway： IEEE， 2020： 278-288.

[8] 李从东，黄浩，张帆顺. 基于演化博弈的领先用户知识共享行为激励机制［J］. 计算机应用， 2021， 41（6）：1785-1791.（LI C D， HUANG H， ZHANG F S. Knowledge sharing behavior incentive mechanism for lead users based on evolutionary game［J］. Journal of Computer Applications， 2021， 41（6）： 1785-1791.）

[9] CHEN Y， ZHANG Y， WANG S， et al. DIM-DS： dynamic incentive model for data sharing in federated learning based on smart contracts and evolutionary game theory［J］. IEEE Internet of Things Journal， 2022， 9（23）： 24572-24584.

[10] ZOU Y， FENG S， NIYATO D， et al. Mobile device training strategies in federated learning： an evolutionary game approach［C］// Proceedings of the 2019 IEEE International Conference on Internet of Things/ Green Computing and Communications/ Cyber， Physical and Social Computing/ Smart Data. Piscataway： IEEE， 2019： 874-879.

[11] 王月平，徐涛. 基于演化博弈的用户接入机制［J］. 计算机应用， 2020， 40（5）：1392-1396.（WANG Y P， XU T. User association mechanism based on evolutionary game［J］. Journal of Computer Applications， 2020， 40（5）： 1392-1396.）

[12] LIM W Y B， NG J S， XIONG Z， et al. Dynamic edge association and resource allocation in self-organizing hierarchical federated learning networks［J］. IEEE Journal on Selected Areas in Communications， 2021， 39（12）： 3640-3653.

[13] FENG S， NIYATO D， WANG P， et al. Joint service pricing and cooperative relay communication for federated learning［C］// Proceedings of the 2019 IEEE International Conference on Internet of Things/ Green Computing and Communications/ Cyber， Physical and Social Computing/ Smart Data. Piscataway： IEEE， 2019： 815-820.

[14] XIAO G， XIAO M， GAO G， et al. Incentive mechanism design for federated learning： a two-stage Stackelberg game approach［C］// Proceedings of the IEEE 26th International Conference on Parallel and Distributed Systems. Piscataway： IEEE， 2020： 148-155.

[15] KHAN L U， PANDEY S R， TRAN N H， et al. Federated learning for edge networks： resource optimization and incentive mechanism［J］. IEEE Communications Magazine， 2020， 58（10）： 88-93.

[16] NIE J， LUO J， XIONG Z， et al. A Stackelberg game approach toward socially-aware incentive mechanisms for mobile crowdsensing［J］. IEEE Transactions on Wireless Communications， 2019， 18（1）： 724-738.

[17] SU Y， FAN W， LIU Y， et al. Game-based pricing and task offloading in mobile edge computing enabled edge-cloud systems［EB/OL］. （2021-01-14） ［2022-08-10］.https：//arxiv.org/pdf/2101.05628.pdf.

[18] ZHAN Y， LI P， QU Z， et al. A learning-based incentive mechanism for federated learning［J］. IEEE Internet of Things Journal， 2020， 7（7）： 6360-6368.

[19] GONG X， DUAN L， CHEN X， et al. When social network effect meets congestion effect in wireless networks： data usage equilibrium and optimal pricing［J］. IEEE Journal on Selected Areas in Communications， 2017， 35（2）： 449-462.

[20] HAN Z， NIYATO D， SAAD W， et al. Game Theory in Wireless and Communication Networks： Theory， Models， and Applications［M］. Cambridge： Cambridge University Press， 2012： 139-143.

[21] HOFBAUER J， SIGMUND K. Evolutionary game dynamics［J］. Bulletin of the American Mathematical Society， 2003， 40（4）： 479-519.

[22] GAO X， FENG S， NIYATO D， et al. Dynamic access point and service selection in backscatter-assisted RF-powered cognitive networks［J］. IEEE Internet of Things Journal， 2019， 6（5）： 8270-8283.

[23] PEJÓ B， TANG Q， BICZÓK G. Together or alone： the price of privacy in collaborative learning［EB/OL］. ［2022-08-10］.https：//arxiv.org/pdf/1712.00270.pdf.

[24] WENG J， WENG J， HUANG H， et al. FedServing： a federated prediction serving framework based on incentive mechanism［C］// Proceedings of the 2021 IEEE Conference on Computer Communications. Piscataway： IEEE， 2021： 1-10.

[25] GONDZIO J. Interior point methods 25 years later［J］. European Journal of Operational Research， 2012， 218（3）： 587-601.

[26] LENG Y， WANG M， MA B， et al. A game-based scheme for resource purchasing and pricing in MEC for Internet of Things［J］. Security and Communication Networks， 2021， 2021： No.1951141.

[27] DENG Y， LYU F， REN J， et al. Improving federated learning with quality-aware user incentive and auto-weighted model aggregation［J］. IEEE Transactions on Parallel and Distributed Systems， 2022， 33（12）： 4515-4529.

[28] ZHAN Y， ZHANG J， HONG Z， et al. A survey of incentive mechanism design for federated learning［J］. IEEE Transactions on Emerging Topics in Computing， 2022， 10（2）： 1035-1044.

Incentive mechanism design for hierarchical federated learning based on multi-leader Stackelberg game

GENG Fangxing1，2， LI Zhuo1，2*， CHEN Xin2

（1（），100101，；2，，100101，）

The existence of privacy security and resource consumption issues in hierarchical federated learning reduces the enthusiasm of participants. To encourage a sufficient number of participants to actively participate in learning tasks and address the decision-making problem between multiple mobile devices and multiple edge servers， an incentive mechanism based on multi-leader Stackelberg game was proposed. Firstly， by quantifying the cost-utility of mobile devices and the payment of edge servers， a utility function was constructed， and an optimization problem was defined. Then， the interaction among mobile devices was modeled as an evolutionary game， and the interaction among edge servers was modeled as a non-cooperative game. To solve the optimal edge server selection and pricing strategy， a Multi-round Iterative Edge Server selection algorithm （MIES） and a Gradient Iterative Pricing Algorithm （GIPA） were proposed. The former was used to solve the evolutionary game equilibrium solution among mobile devices， and the latter was used to solve the pricing competition problem among edge servers. Experimental results show that compared with Optimal Pricing Prediction Strategy （OPPS）， Historical Optimal Pricing Strategy （HOPS） and Random Pricing Strategy （RPS）， GIPA can increase the average utility of edge servers by 4.06%， 10.08%， and 31.39% respectively.

hierarchical federated learning; incentive mechanism; pricing strategy; multi-leader Stackelberg game; evolutionary game

1001-9081（2023）11-3551-08

10.11772/j.issn.1001-9081.2022111727

2022⁃11⁃21；

2023⁃04⁃03；

北京市自然科学基金资助项目（4232024）； 国家重点研发计划项目（2022YFF0604502）； 国家自然科学基金资助项目（61872044）； 北京市青年拔尖人才项目。

耿方兴（1999—），男，河南驻马店人，硕士研究生，主要研究方向：边缘计算； 李卓（1983—），男，河南南阳人，副教授，博士，CCF会员，主要研究方向：移动无线网络、分布式计算； 陈昕（1965—），男，江西南昌人，教授，博士，CCF会员，主要研究方向：网络性能评价、网络安全。

TP393

A

2023⁃04⁃04。

This work is partially supported by Beijing Natural Science Foundation （4232024）， National Key Research and Development Program of China （2022YFF0604502）， National Natural Science Foundation of China （61872044）， Beijing Municipal Program for Young Talents.

GENG Fangxing， born in 1999， M. S. candidate. His research interests include edge computing.

LI Zhuo， born in 1983， Ph. D.， associate professor. His research interests include mobile wireless network， distributed computing.

CHEN Xin， born in 1965， Ph. D.， professor. His research interests include network performance evaluation， network security.