流密码非线性布尔函数可重构运算单元设计方法RA-NLBF

张宗仁，戴紫彬，刘燕江，张晓磊

流密码非线性布尔函数可重构运算单元设计方法RA-NLBF

张宗仁1，2，戴紫彬1*，刘燕江1，张晓磊1

（1.解放军信息工程大学，郑州 450001； 2.31642部队，云南 临沧 677000）（ ∗ 通信作者电子邮箱daizb2004@126.com）

分组密码中的S盒（多输出）以及流密码中的反馈函数都需要特殊的布尔函数来保证密码算法的安全性。为解决现有流密码算法中非线性布尔函数（NLBF）可重构硬件运算单元资源占用过大、时钟频率低等问题，提出一种高效的基于与非锥（AIC）的NLBF可重构运算单元设计方法（RA-NLBF）。以密码学理论为基础，在着重分析多种流密码算法的NLBF特性，提取了涵盖与项次数、与项个数、输入端口数等NLBF函数特征的基础上，提出基于“混合极性Reed-Muller（MPRM）”和“传统布尔逻辑（TB）”双逻辑混合形式的NLBF化简方法，NLBF的与项数量减少29%，形成了适用于AIC的NLBF表达式；根据化简后的表达中与项个数、与项次数分布等特征，设计了可重构AIC单元和互联网络，形成可满足现有公开流密码算法中的NLBF运算的可重构单元。基于CMOS 180 nm工艺对提出的RA-NLBF进行逻辑综合验证，结果显示该方法的面积为12 949.67 μm²，时钟频率达到505 MHz，与现有相同功能的单元可重构序列密码逻辑单元（RSCLU）相比，面积减少了59.7%，时钟频率提高了37.3%。

流密码；可重构实现；非线性布尔函数；与非锥；混合极性RM

0 引言

基于非线性反馈移位寄存器的流密码正在成为现代流密码的主流设计。运算速度快、硬件占用空间小和功耗低的特性使此类密码更适合需要安全通信的资源受限应用。为了满足流密码算法安全特性并提高流密码算法中布尔函数的平衡性、高代数次数、高非线性、相关免疫性等，设计者选择目前公认的各方面性质较为平衡的非线性布尔函数（Non-Linear Boolean Function， NLBF）作为流密码的构建块［1］。目前，NLBF的硬件实现包括通用实现和专用实现两种方式。随着可重构逻辑阵列器件的兴起和不断发展，NLBF的通用实现方式正成为一个重要的研究方向。

通用实现方式主要集中在现场可编程阵列（Field-Programmable Gate Array， FPGA）和粗粒度可重构阵列（Coarse-Grained Reconfigurable Array， CGRA），目前学术界普遍利用FPGA的查找表（Look Up Table， LUT）、选择器（MUX）和寄存器等器件来实现各种布尔函数。文献［2］中提出了一种基于“AND-LUT”混合的NLBF实现方法，其中与阵列用于实现高扇入逻辑电路，LUT用于实现低扇入逻辑结构，相较于其他基于FPGA中LUT级联的结构，资源面积减少了46%；但未针对密码算法中的NLBF运算进行优化，资源利用率低。文献［3］中利用布尔代数理论将NLBF进行分解运算，将高效布尔运算分解成低次，采用流水线技术使各级实现不同的函数功能；但消耗的资源会随着变量增加呈指数级增长。文献［4］中提出了一种面向对称密码处理的可重构结构，整体结构每行通过灵活的树形互连，降低了互连复杂度，减少了面积，可完成大部分分组密码和少部分流密码的功能，具有较低的功耗及较高的面积利用率；但处理单元对NLBF适用性不强。文献［5］中以提高资源利用率为目标，以变量频次为约束改进适配算法，并设计单元互联结构，将资源利用率提高到91%以上；但该算法以LUT数量为利用率的计算数据，资源占用仍然较大。文献［6］中分别设计了NLBF的线性和非线性部分，其中非线性部分的高次项采用与-异或阵列，低次项部分采用共享两输入端口的LUT级联结构实现；虽然架构可以满足现有公开密码算法的NLBF，但高次项部分占用资源过大，同时低次项的共享端口给软件映射增加了难度。文献［7］在文献［5］研究的基础上，增加部分电路以实现多种S盒的功能，在功能上进行了扩展，提高了资源利用率；但增加了部分电路，在延迟上也没有改进。总的来说，现有研究均是基于LUT设计的NLBF可重构运算单元，然而LUT的高灵活性是以面积、延迟和功耗为代价的，密码领域的逻辑函数结构差别大、数量少，对于大位宽的复杂NLBF，由于LUT单元面积与输入端口数目呈指数增长关系，利用大尺寸LUT单元实现时资源占用较大，而利用小尺寸LUT单元实现时级联复杂，延迟增加；对于简单的NLBF，可重构单元资源冗余过大，利用率低。

本文首先从流密码的NLBF设计原则入手，总结NLBF特性，针对NLBF输入端口多、分布广和存在极高与项次数特点，利用新兴的与非锥（And-Inverter Cone， AIC）［8］结构的大位宽输入和多输出特性实现NLBF，针对性地简化NLBF表达式，提出了一种基于AIC的NLBF的可重构运算单元设计方法RA-NLBF（Reconfigurable operation unit AIC-based for Non-Linear Boolean Function），可以有效降低资源占用问题，避免了复杂的互联关系，并降低了电路延迟。本文设计的可重构运算单元可以兼容现有流密码算法的所有NLBF，并且资源占用小，时钟频率明显提高。

1 流密码中NLBF特性及实现方式分析

1.1　NLBF特性分析

流密码（序列密码）因加解密原理简单，算法迅速快捷，在保密通信中扮演着不可替代的角色。布尔函数作为流密码非线性组合部分的重要部件，它的密码学性质直接关系到整个流密码系统的安全性。密码学指标［9］主要为：平衡性准则、代数次数（线性复杂度）、非线性度、相关免疫（弹性）和代数免疫度。

但诸多安全性指标很难同时兼顾，彼此制约，指标之间本身就是矛盾的关系。例如：

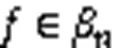
为了更直观地分析流密码中NLBF的特性，本文提取近几年新设计的轻量级流密码和传统经典流密码中的NLBF，对与项次数分布和端口数目等特征进行统计分析，如表1所示。其中：1次项占比约30.6%，1次项是函数平衡性的保证；2次与项占比约34.2%，大部分两两之间无公共变量，这是高非线性度的特征要求；3次与项和4次与项总占比约31.8%，这是为了兼顾高非线性同时提高代数次数；高于4次项部分仅占3.4%，仅存在于部分算法中，这是高代数次数与高相关免疫性、高非线性之间的中和结果。根据各个安全指标的定义可知，变元个数越大，各种安全特性呈线性（指数）变化。流密码中NLBF输入端口数目分布集中于［13，18］，占比约44.9%，其中超过24个输入端口的仍占比约14.3%，13个输入端口以上占73.5%，增加输入端口数目可以尽可能兼顾几种设计原则，从而提高安全性。

表1　流密码NLBF与项次数、输入端口频率分布

根据NLBF的设计原则和表1统计结果，总结流密码中NLBF具有以下特点：

1）高次与项（4次以上）仅占比约3.4%，仅有个别NLBF涉及高次与项，高于7次与项的仅有Toyocrypt-hs1算法。

2）低次与项占比约96.6%，但很多算法中低次与项之间关系交叉相关，或完全无关。

3）端口数13以上占比约73.5%，分布范围也比较大，即NLBF位宽较大，特别是在轻量级流密码中得到越来越多使用。

1.2　基于LUT结构的NLBF实现方式分析

表2　密码算法中的NLBF任意4变量组合形式

2 基于AIC的NLBF实现设计分析

2.1　AIC原理

2012年，瑞士洛桑理工大学Parandeh博士等受到用于电路映射工具的基本映射单元AIG（And-Inverter Graphs）［10］的启发，提出了一种更贴近电路逻辑表达式的通用逻辑单元与非锥（AIC）结构，这种深度约束型逻辑结构在提高可重构阵列性能、面积和功耗等指标上展现出了可观的潜力。

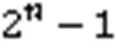
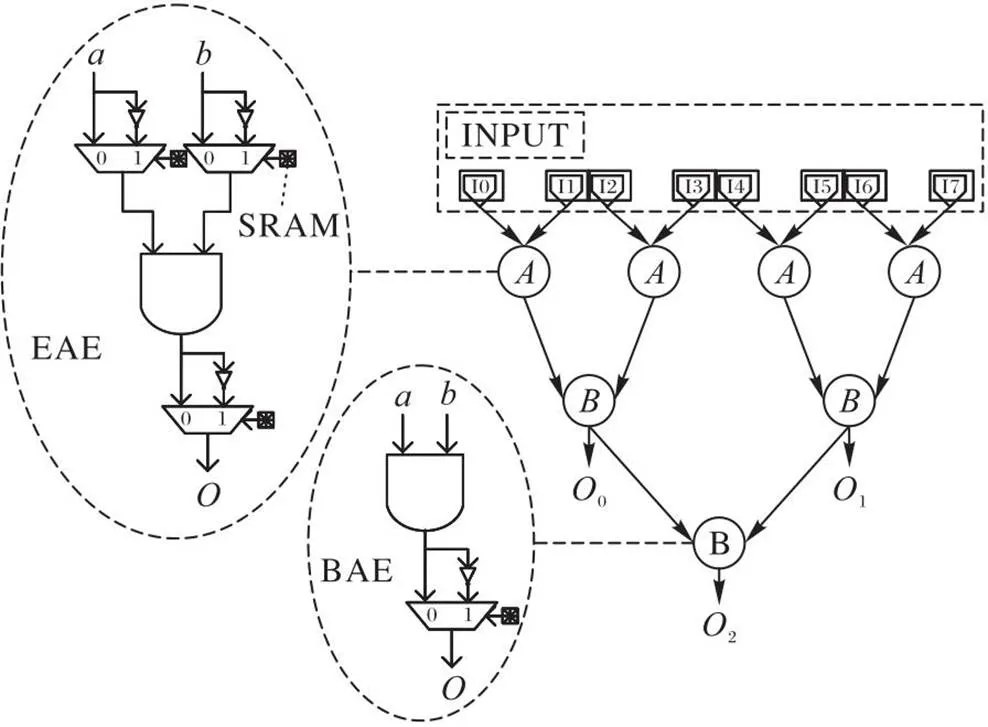
图1　三级AIC结构

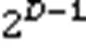
2.2　AIC的结构特点分析

近年来，黄志洪［11］对AIC中间节点进行定制化改进，大幅改善了AIC结构由于配置信息不同而可能造成的延迟毛刺并降低了延迟；在大量不同类型逻辑电路测试后，对输入端和输出端的交叉开关（Crossbar）进行优化设计［12］，与基于LUT相比，基于AIC的FPGA全局面积减少了10%，延迟降低了30%［13］。

从1.1节可知，73.5%的流密码算法中NLBF的输入变量在13个以上，使用尺寸为13的LUT显然资源浪费极大，若采用多级互联方式，会造成资源浪费和延迟增加。即使某些架构可以共享LUT的输入端口，但由于流密码算法中高非线性度的要求，需要尽可能避免公共变量的与项，因此可以共享的端口也极有限，节省资源有限。相较于LUT结构，由于AIC结构的多输入多输出的特点，一个4-AIC可以满足16个2次以下的与项，或8个4次以下的与项，与项之间相互独立。由1.1节可知，2次以下的与项占流密码与项总数的64.8%，4次以下与项占流密码与项总数的96.6%。因此，对于流密码算法中NLBF，AIC结构作为硬件实现电路有显著的优势。

3 流密码中NLBF化简

3.1　基于AIC结构实现布尔函数的特点分析

一个任意的2变量布尔函数有10种表达形式（除了常数项和1变量形式外），由第2章可知，AIC结构的一个节点可以实现8种2输入逻辑，不能实现的2种分别是异或、同或。一个异或（同或）逻辑若采用多节点级联方式，需要3个节点，其中一条支路的输入和另一条支路完全相同，则一条支路端口被重复占用，整体AIC的输入变量减少。对一个4‑AIC，表达式第一级运算出现异或，则占用3个节点、2级电路，输入变量最多14个；第二级出现，则占用7个节点、3级电路，输入变量最多12个；第三级出现异或，则占用全部4-AIC节点15个，输入变量最多8个。由此可见，AIC结构不适合异或运算的实现，因此在多个AIC级联时，将异或逻辑拆解，避免在同一个AIC单元中实现异或。

AIC结构另一个显著特点是输入和输出可以根据需要取反。在代数理论中，多种布尔逻辑通过输入或输出取反，或输入变量位置变换后具有相同的函数结构，即与项个数和次数完全相同，则称这些逻辑函数NPN（Negation-Permutation-Negation）等价。通过NPN等价分类，可以大幅减少函数的类别，利用相同的电路结构实现更多的逻辑功能。在函数化简时，应充分利用此特性，用最简的NPN等价类表达式，取代同一等价类中复杂的表达式。

3.2　NLBF化简

根据3.1节分析结果，本文提出一种“混合极性RM（Mixed Polarity Reed-Muller， MPRM）”［14］和“传统布尔（Traditional Boolean function， TB）逻辑”双逻辑混合化简NLBF表达式的方法，以减少与项，并将异或运算剥离到其他电路中实现。

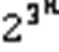
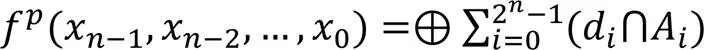
表3　与、的关系

AIC结构中的输入取反操作，对应MPRM逻辑的极性配置。输出取反操作可以将“与”逻辑和“或”逻辑进行互换。在布尔运算中一个高次的与项无法通过低次与项异或得到，因此，本文针对密码算法布尔函数特性和AIC结构特点，提出两种情况下的消除与项的方法。

1）利用极性转化消除低次与项。

根据异或运算的性质，式（3）是两种转化情况：第一种，利用异或结合律对不同的变量取反以消除低次与项；第二种，同一个函数中变量既可以存在原相也可以存在反相，以达到减少与项的目的。在AIC结构中通过配置输入取反和输出取反即可实现。

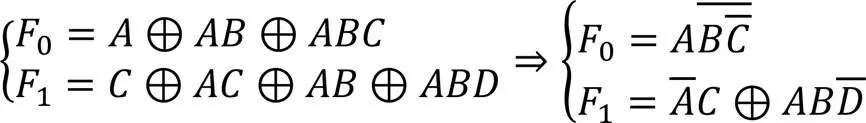
2）利用AIC多输出功能复用相同与项。

例如Toyocrypt-hs1算法中有63次与项、17次与项以及4次与项。

经过分析，17次与项包含于63次与项中，4次与项包含于63次与项中。如式（5）所示，用极性转化的方法只能消除一个17次与项或一个4次与项。若将4次与项的输出直接复用，则可以消除2个与项只用一个63次与项的电路实现函数。

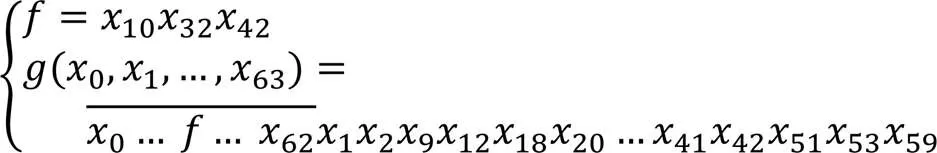
经过化简后，与项个数得到明显优化，3次项减少66.5%，总项数减少28.1%，Toyocrypt-hs1算法减少一个4次和一个17次与项，资源占用得到较大优化。1次与项和2次与项在AIC结构中均要使用一个可编程2输入与节点，消耗同等的资源，与化简前相比，1次与项和2次与项总数量减少26.6%。在AIC结构中，3次与项和4次与项占用资源相同且大概是2次与项的3倍，5次与项和6次与项占用资源相同且大概是2次与项的7倍，一个63次与项资源占用大概是2次与项的63倍。化简后总体资源占用至少降低29%。

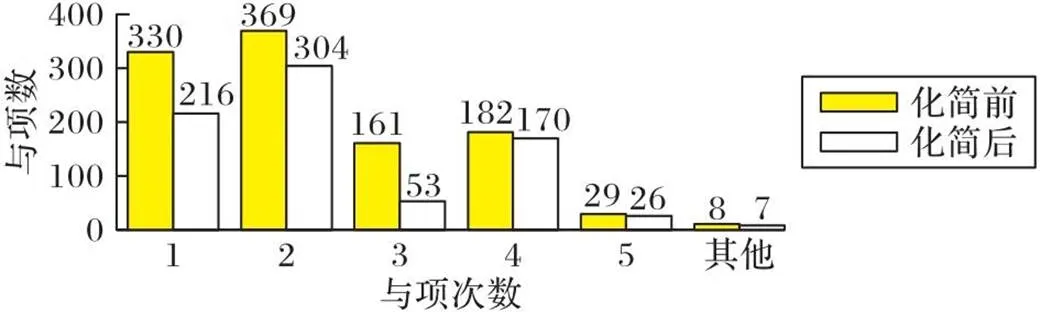
图2　NLBF化简前后结果比较

4 NLBF的可重构单元设计

4.1　可重构运算单元总体架构

NLBF可重构运算单元如图3所示，主要分为三大部分：AIC运算（AIC operation）、异或阵列（Xor array）和配置存储单元（Configuration Reg unit）。其中AIC运算单元以基于AIC设计改进型AIC-g作为基本构件，采用3个Part组合，共20个2‑AIC-g、6个3-AIC-g和1个6-AIC-g（此部分在下一节详细分析）。AIC运算部分单个Part为64 bit输入（共计192 bit输入），此单元可以实现最多64次与项，最多48个4次与项和最多96个2次与项的函数，生成4 bit输出。

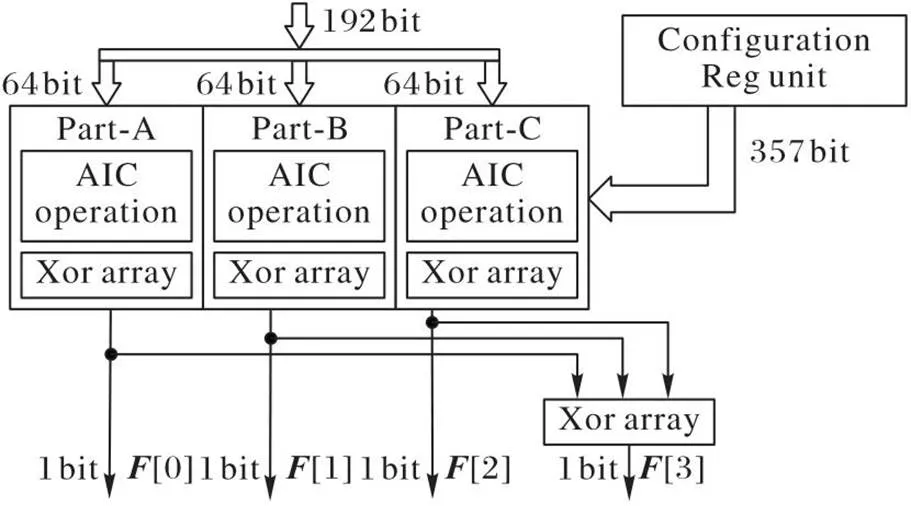
图3　RA-NLBF总体布局

4.2　AIC结构的功能定制设计和级联结构分析

对化简后的NLBF中与项次数和异或操作进行分析：

1）与项次数大部分不高于4次，有极个别大于8次，但只出现在了一个算法中，且可以化简合并成一个与项；与项最后一级不需要取反。

2）大部分异或运算出现在第一级、第二级、第三级，极个别函数中，异或运算出现在四级以上（目前仅有Toyocrypt-hs1中存在）。

由于AIC结构对异或运算支持能力差，将AIC-g的输出直接送入异或阵列中，通过配置信息选择需要的与项结果，避免在AIC-g中计算异或。如表4，对32种NLBF进行适配，本文中一个3-AIC-g可以转变为2个2-AIC-g，一个6‑AIC‑g可以转变为16个2-AIC-g，表中以一个2-AIC-g为基本单位。由表4中2-AIC-g占用情况分析可得，最多需要48个，最少需要2个，大部分算法在16个以下。

表4　常用流密码算法［15］NLBF的资源占用

注：Z表示钟控函数，F表示反馈函数，M表示密钥生成函数，V表示初始化，S表示输出函数。

通过以上分析，如图4，将10个2-AIC-g与3个3-AIC-g并行为一组，选择所需AIC输出进入异或阵列生成1 bit输出（Part-A），另一组相同单元（Part-B）可生成第2 bit输出。如图5，为满足极少数高次项需求，增加一个6-AIC-g单元，所有输出经过选择后进入异或阵列生成1 bit输出（Part-C）。单个Part可以实现大部分算法的NLBF，3个Part输出异或，生成一个新的1 bit输出，可实现某些较复杂的NLBF。

5 NLBF映射与实验结果分析

Achterbahn加密和解密通过将二进制伪随机序列（称为密钥流）分别按位添加到明文字符串或密文字符串实现。Achterbahn-80的密钥流生成器部署了11个原始二进制非线性反馈移位寄存器，Achterbahn-128的密钥流生成器部署了13个原始非线性反馈移位寄存器，并包含Achterbahn-80的密钥流生成器作为子结构。Achterbahn的NLBF目前也被许多轻量级流密码采用，如Lizard。算法中密钥生成函数直接采用了Achterbahn算法中的A10函数。如表5，本文对Achterbahn-A10算法的化简过程进行演示。

图4　Part-A（Part-B）的级联结构

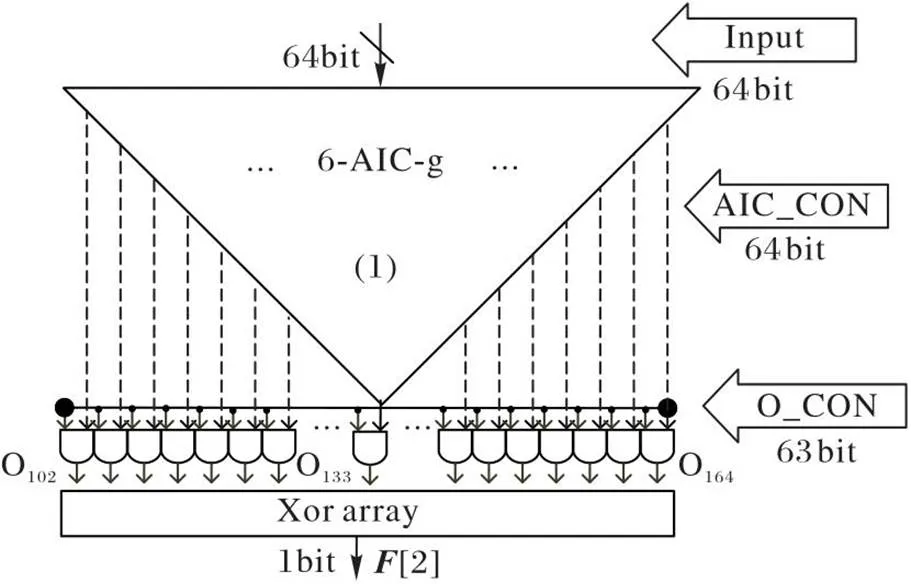
图5　Part-C的级联结构

表5　Achterbahn-80/128-A10适配结果

根据图3可知，最长关键路径经过Patr⁃C部分由［3］输出，设定均选用2输入1输出的MUX、NAND、XOR标准单元，则⁃AIC⁃g延迟计算公式为：

在CMOS 180 nm工艺下进行逻辑综合，各项性能指标如表6所示。总延时为1.98 ns，总面积为12 949.67 μm2，等效两输入与非门约为0.129万门，此时的时钟频率为505 MHz。

表6　可重构单元的面积和延迟

在CMOS 180 nm工艺下，将性能与以往设计进行对比，如表7所示，2003年提出的RNF［16］架构主要是对寄存器并行化的设计，对资源面积和时钟频率未做优化，它的延迟与本文相当，面积却增加205倍；2009年提出的RPNF［17］对NLBF进行了简单优化，等效门数为1.31万门，延迟为6.01 ns；2013年提出的TNF［18］对NLBF表达式进行处理，将线性与非线性分开设计，但在优化时只对线性部分进行优化，事实上非线性部分占用资源更大，运算宽度可以达到256 bit，等效门数0.44万门，延迟为5.24 ns；2016年提出的可重构序列密码逻辑单元（Reconfigurable Logic Unit for Sequence Cryptographic， RSCLU）［5］以提高NLBF资源利用率为目的，提取函数的高频变量作为共享LUT输入，有效降低了可重构单元的资源占用，但资源利用率以LUT为基本单元，未考虑LUT单元自身的资源冗余问题。2019的文献［6］的方法仅在一定程度上改善了外部互联，但面积占用和延迟都不理想。2022年发表的SNBFM［7］对S盒的实现进行了改进，并用65 nm工艺节点实现，增加了电路，延长了关键路径，理论上面积和延迟都要比RSCLU大。与RSCLU相比，文本方法面积占用减少59.7%，延迟降低37.3%，专用性更强，资源利用较充分。

表7　不同方法的性能对比

6 结语

本文提出的基于AIC结构的可重构NLBF运算单元设计方法RA-NLBF，使用较少的资源，获得明显的时钟频率提升。本文针对现有算法进行分析，因此结构的通用性可能受影响；但从理论上也进行了定性分析，设计方法可推广，适用于对未来新出现的NLBF可重构单元设计。未来还将在映射算法和外部互联结构作进一步研究。

[1] CRAMA Y， HAMMER P L. Boolean Functions： Theory， Algorithms， and Applications［M］. Cambridge： Cambridge University Press， 2011： 564-607.

[2] CHEN L G， LAI J M， TONG J R. An AND-LUT based hybrid FPGA architecture［J］. Chinese Journal of Semiconductors， 2007， 28（3）：398-403.

[3] SARKAR P， MAITRA S. Efficient implementation of "large" stream cipher systems［C］// Proceedings of the 2001 International Workshop on Cryptographic Hardware and Embedded Systems， LNCS 2162. Berlin： Springer， 2001： 319-332.

[4] WANG B， LIU L. A flexible and energy-efficient reconfigurable architecture for symmetric cipher processing［C］// Proceedings of the 2015 IEEE International Symposium on Circuits and Systems. Piscataway： IEEE， 2015： 1182-1185.

[5] 戴紫彬，王周闯，李伟，等.可重构非线性布尔函数利用率模型研究与硬件设计［J］. 电子与信息学报， 2017， 39（5）： 1226-1232.（DAI Z B， WANG Z C， LI W， et al. Hardware implementation and utilization model research for reconfigurable non-linear Boolean function［J］. Journal of Electronics and Information Technology， 2017， 39（5）： 1226-1232.）

[6] SU Y， SHEN J， WANG W. Reconfigurable design and implementation of nonlinear Boolean function for cloud computing security platform［J］. International Journal of Information and Computer Security， 2019， 11（2）：145-159.

[7] 连宜新，陈韬，李伟，等. 两类非线性密码组件可重构研究与电路设计［J］. 计算机工程， 2022， 48（2）：156-163， 172.（LIAN Y X， CHEN T， LI W， et al. Reconfigurable research and circuit design of two types of nonlinear cryptographic components［J］. Computer Engineering， 2022， 48（2）：156-163， 172.）

[8] PARANDEH-AFSHAR H， BENBIHI H， NOVO D， et al. Rethinking FPGAs： elude the flexibility excess of LUTs with and-inverter cones［C］// Proceedings of the 2012 ACM/SIGDA International Symposium on Field Programmable Gate Arrays. New York， ACM， 2012：119-128.

[9] 葛徽. 流密码中密码函数的设计与分析［D］. 西安：西安电子科技大学， 2021：11-23.（GE H. Analysis and design of cryptographic functions for stream ciphers［D］. Xi’an： Xidian University， 2021： 11-23.）

[10] MISHCHENKO A， CHATTERJEE S， BRAYTON R. DAG-aware AIG rewriting： a fresh look at combinational logic synthesis［C］// Proceedings of the 43rd ACM/IEEE Design Automation Conference. New York： ACM， 2006： 532-535.

[11] 黄志洪.现场可编程门阵列（FPGA）异质逻辑与存储互连结构研究［D］.北京：中国科学院大学，2016：75-91.（HUANG Z H. Research on heterogeneous logic and storage interconnection structure of Field Programmable Gate Array （FPGA）［D］. Beijing： University of Chinese Academy of Sciences， 2016： 75-91.）

[12] 黄志洪，李威，杨立群，等.一种基于与非锥簇架构FPGA输入交叉互连设计优化方法［J］.电子与信息学报，2016，38（9）： 2397-2404.（HUANG Z H， LI W， YANG L Q， et al. An input crossbar optimization method for and-inverter cone based FPGA［J］. Journal of Electronics and Information Technology， 2016， 38（9）： 2397-2404.）

[13] RAI S， NATH P， RUPANI A， et al. A survey of FPGA logic cell designs in the light of emerging technologies［J］. IEEE Access， 2021， 9： 91564-91574.

[14] 李辉. 混合极性Reed-Muller逻辑电路功耗和面积优化［D］. 宁波：宁波大学， 2011：41-45.（LI H. Power and area optimization of mixed polarity Reed-Muller logic circuits［D］. Ningbo： Ningbo University， 2011：41-45.）

[15] 赵石磊，刘玲，黄海，等. 流密码算法、架构与硬件实现研究［J］. 密码学报， 2021， 8（6）： 1039-1057.（ZHAO S L， LIU L， HUANG H， et al. Algorithm， architecture and hardware implementation of stream cipher［J］. Journal of Cryptologic Research， 2021， 8（6）： 1039-1057.）

[16] 秦晓懿，王瀚晟，曾烈光.线性和非线性寄存器系统的并行化技术［J］. 电子学报，2003，31（3）：406-410. （QIN X Y， WANG H S， ZENG L G. Parallelization techniques for linear and non-linear register systems［J］. Acta Electronica Sinica， 2003， 31（3）： 406-410.）

[17] 李伟.面向序列密码的反馈移位寄存器可重构并行化设计技术研究［D］.郑州：解放军信息工程大学，2009：34-35.（LI W. Research on technology of reconfigurable parallel feedback shift register targeted at stream cipher［D］. Zhengzhou： PLA Information Engineering University， 2009： 34-35.）

[18] 陈韬，杨萱，戴紫彬，等.面向序列密码的非线性反馈移位寄存器可重构并行化设计［J］.上海交通大学学报，2013，47（1）：28-32. （CHEN T， YANG X， DAI Z B， et al. Design of a reconfigurable parallel nonlinear feedback shift register structure targeted at stream cipher［J］. Journal of Shanghai Jiao Tong University， 2013， 47（1）： 28-32.）

RA-NLBF： design method of reconfigurable operation unit for stream cipher non-linear Boolean function

ZHANG Zongren1，2， DAI Zibin1*， LIU Yanjiang1， ZHANG Xiaolei1

（1，450001，；231642，677000，）

Both the S-box （multiple outputs） in block ciphers and the feedback function in stream ciphers require special Boolean functions to ensure the security of the cipher algorithm. To solve the problems of excessive resource consumption of reconfigurable hardware operation units and low clock frequency caused by Non-Linear Boolean Function （NLBF） in the existing algorithms of stream cipher， a high-efficiency AIC（And-Inverter Cone）-based design scheme for NLBF reconfigurable operation units was proposed， namely RA-NLBF. Based on the theories of cryptography， after analyzing the NLBF characteristics of various stream cipher algorithms and extracting the function features of NLBF including the times of AND terms， the number of AND terms， and the number of input ports， an NLBF simplification method based on the dual-logic hybrid form of “Mixed Polarity Reed-Muller （MPRM）” and “Traditional Boolean function （TB）” was proposed， which reduced the number of NLBF AND terms by 29% and formed an NLBF expression suitable for the AIC. Based on the simplified expression characteristics， such as the distribution of the number of AND terms and the times of AND terms， reconfigurable AIC units and interconnection networks were designed to form the reconfigurable units that can satisfy the NLBF operation in the existing public stream cipher algorithms. The proposed RA-NLBF was verified by logic synthesis based on CMOS 180 nm technology， and the results show that the area of RA-NLBF is 12 949.67 μm²， and the clock frequency reaches 505 MHz， which is a 59.7% reduction in area and a 37.3% increase in clock frequency compared with Reconfigurable Logic Unit for Sequence Cryptographic （RSCLU）， an existing method with the same function.

stream cipher; reconfigurable implementation; Non-Linear Boolean Function (NLBF); And-Inverter Cone (AIC); Mixed Polarity Reed-Muller (MPRM)

1001-9081（2023）11-3527-07

10.11772/j.issn.1001-9081.2022111690

2022⁃11⁃15；

2023⁃03⁃07；

“核高基”国家科技重大专项（2018ZX01027101⁃004）。

张宗仁（1994—），男，湖北襄阳人，硕士研究生，主要研究方向：安全专用芯片设计、可重构计算； 戴紫彬（1966—），男，河南西峡人，教授，博士生导师，博士，主要研究方向：信息安全、体系结构； 刘燕江（1990—），男，河南南阳人，博士，主要研究方向：安全专用芯片设计、侧信道攻击； 张晓磊（1992—），男，河北青县人，硕士研究生，主要研究方向：安全专用芯片设计。

TP309.7； TN492

A

2023⁃03⁃20。

This work is partially supported by National Science and Technology Major Project （2018ZX01027101-004）.

ZHANG Zongren， born in 1994， M. S. candidate. His research interests include special security chip design， reconfigurable computing.

DAI Zibin， born in 1966， Ph. D.， professor. His research interests include information security， architecture.

LIU Yanjiang， born in 1990， Ph. D. His research interests include special security chip design， side-channel attacks.

ZHANG Xiaolei， born in 1992， M. S. candidate. His research interests include special security chip design.