基于社区改变量估计的非均匀时间片划分方法

罗香玉，闫克，卢琰，王甜，辛刚

基于社区改变量估计的非均匀时间片划分方法

罗香玉1*，闫克1，卢琰1，王甜1，辛刚2

（1.西安科技大学 计算机科学与技术学院，西安 710054； 2.中国航空工业集团公司西安航空计算技术研究所，西安 710119）（ ∗ 通信作者电子邮箱luoxiangyu@xust.edu.cn）

动态网络时间片划分方法对社区演化分析结果的准确性具有重要影响，但社区随时间及网络拓扑改变呈现非线性的变化，现有均匀时间片划分以及基于网络拓扑改变量的非均匀时间片划分方法在捕捉社区演化事件方面均效果不佳。为此，提出一种基于社区改变量估计的非均匀时间片划分方法，其中社区改变量通过变化后网络期望达到的社区模块度与直接应用网络变化前的社区发现结果获得的社区模块度之差来定量描述。首先，基于时间序列分析建立社区模块度预测模型；其次，使用该模型预测变化后网络期望达到的社区模块度，并求得社区改变量的估计值；最后，当该估计值超过预先设置的阈值时即生成一个新的时间片。在两个真实网络数据集上的实验结果显示，相较于传统的均匀时间片划分方法和基于网络拓扑改变量的非均匀时间片划分方法，所提方法在动态网络数据集Arxiv HEP-PH上的识别社区消失事件方面分别提早1.10 d和1.30 d，识别社区形成事件方面分别提早8.34 d和3.34 d，识别出的社区缩小、扩大事件总数分别增加10个和1个；在Sx-MathOverflow数据集上的识别社区消失事件方面分别提早3.30 d和1.80 d，识别社区形成事件方面分别提早6.41 d和2.97 d，识别出的社区缩小、扩大事件总数分别增加15个和7个。

动态网络；时间片划分；社区演化；时间序列分析；社区发现；社区模块度

0 引言

近年来，社区演化分析已成为动态网络的研究热点［1-4］。它旨在发现动态网络潜在的演化规律，为预测社区的演化行为提供依据和信息。社区演化分析在众多领域都有广泛的应用。例如，应用于蛋白质交互网络时［5-6］，可以根据已知的蛋白质拓扑结构和交互关系对未知蛋白质的功能和行为进行预测；应用于舆情监测和引导时［7-8］，有助于掌握负面舆论的传播路径；应用于公共卫生领域时，可以为预测传染病的传播提供有价值的信息，提前制定应对措施，防止传染病蔓延［9］。

社区演化分析过程主要分为三个阶段［10］：第一阶段将动态网络划分为一系列能够准确捕获社区演化事件的快照，这一阶段主要依赖合理的时间片划分方法；第二阶段对划分得到的网络快照分别进行社区发现，获取各个快照上的全部社区；第三阶段通过比较两个相邻快照的社区发现结果识别社区演化事件。其中后两个阶段社区发现和社区演化事件识别已得到较深入的研究，但第一阶段时间片划分研究尚不充分。

时间片划分方法对社区演化分析结果的准确性具有重要影响［11-14］。理想的时间片划分方法能够以最少数量的快照捕获所有的社区演化事件，设计出理想的时间片划分方法是一项极具挑战性的工作。由于社区并非随时间匀速变化，均匀时间片划分方法［15-18］效果不佳，最佳时间片长度应根据社区演化速度不断调整，呈现出非均匀的分布。

现有的非均匀时间片划分方法通过计算网络拓扑的改变量获得时间片划分结果。当网络拓扑改变量超过预先设置的阈值时，则生成一个新的时间片。衡量网络拓扑改变量的一个典型指标是网络变化前后边集的Jaccard系数［19］，该系数值越小，则网络拓扑改变量越大。然而，社区随网络拓扑改变呈非线性变化。在一些情况下，删除或添加大量边仍不会导致社区演化，但在另一些情况下，删除或添加少量边即会导致社区演化。因此，基于网络拓扑改变量的非均匀时间片划分方法可能会产生不捕获任何演化事件的冗余快照或者跳过存在演化事件的有效快照。

本文提出一种基于社区改变量估计的非均匀时间片划分方法。该方法不计算网络拓扑的改变量，而是直接估计相邻两个时间片之间的社区改变量，当社区改变量超过某个阈值，则生成一个新的时间片。主要挑战是在网络动态变化之后社区未知条件下如何估计社区的改变程度。

本文的主要工作如下：

1）分析现有时间片划分方法导致社区演化分析结果不准确的原因。由于社区演化与时间、网络拓扑改变量均呈非线性关系，均匀时间片划分方法和基于网络拓扑改变量的非均匀时间片划分方法均会降低社区演化分析结果的准确性。

2）提出一种基于社区改变量估计的非均匀时间片划分方法，其中社区改变量通过变化后网络期望达到的社区模块度与直接应用网络变化前的社区发现结果获得的社区模块度之差来定量描述。期望达到的社区模块度则通过建立基于时间序列分析的社区模块度预测模型进行估计。

3）在真实数据集上对所提方法的有效性进行验证，结果表明，与现有时间片划分方法相比，本文方法能够更及时地发现社区生成和社区消失事件，并发现更多数量的社区扩大和社区缩小事件，社区演化分析结果的准确性得到有效提升。

1 相关工作

社区演化分析过程的三个阶段相关工作分别总结如下。

1.1　时间片划分

时间片划分旨在将动态网络离散化为一系列的快照。它对社区演化分析结果的准确性具有重要影响。现有的动态网络时间片划分方法一般分为两类［20］：均匀时间片划分方法和非均匀时间片划分方法。均匀时间片划分方法采用固定时间间隔将动态网络离散为若干个快照，因实现机制简单而被广泛使用；非均匀时间片划分方法则会将动态网络离散为不等时间间隔的若干个快照，实现机制相对复杂。

根据时间片长度的确定方式，均匀时间片划分可以进一步细分为两个子类：基于人工经验的方法和基于网络特征分析的方法。

基于人工经验确定时间片长度的方法应用最为广泛。Bhat等［21］提出了用于跟踪在线社交网络中分层和重叠社区演变的框架HOCTracker，实验中时间片的长度指定为5 a。Wang等［22］提出了基于拓扑势场中核心节点变化的社区演化事件跟踪方法，实验中时间片长度指定为1 d。Qiao等［23］提出了基于强弱事件的社区演化分析框架，实验中使用了两个数据集，时间片长度分别指定为1 a和1个月（使用的是2008年的数据集，该时间片长度为自然月）。Xu等［24］提出了一种两阶段社区演化分析方法（Error Accumulation Sensitive-Superspreaders And Superblockers， EAS-SAS），解决了社区发现中增量算法导致的累积误差问题以及社区演化事件识别中核心节点贡献度异构性的问题，实验中两个数据集的时间片长度分别指定为1 a和1 d。

基于网络特征分析的均匀时间片划分方法也被广泛使用。对于预设的每个时间片长度值，Tajeuna等［11］分析了相邻快照间新增节点、离开节点和保持节点各自所占的比例，最终选择的时间片长度能够保证相邻快照在新增和离开节点比例以及保持节点比例间取得最佳的平衡。

非均匀时间片划分方法通常会持续评估网络拓扑的改变量，当改变量超过某个阈值时生成一个新的时间片。Çolak等［25］和Orman等［26］通过计算两个相邻快照的Jaccard系数评估网络拓扑的改变程度。Jaccard系数值越大，网络拓扑改变量越小。

由于社区演化与时间以及与网络拓扑的改变量均呈非线性关系，均匀时间片划分方法和基于网络拓扑改变量的非均匀时间片划分方法效果不佳。为此，本文提出一种基于社区改变量估计的非均匀时间片划分方法。该方法直接估计社区改变的程度，并在改变程度超过一定阈值时生成新的时间片。本文方法旨在不增加快照数量的情况下更全面更及时地识别社区演化事件。

1.2　社区发现

社区发现旨在找出每个网络快照上的全部社区。现有研究主要包括三类方法：基于边消除策略的方法、基于社区质量指标优化策略的方法以及基于标签传播策略的方法。基于边消除策略的方法通过逐一识别和消除社区之间的边，将网络划分为若干社区，代表性算法是GN（Girvan-Newman算法）［27］；基于社区质量指标优化策略的方法定义模块度等度量指标评价社区质量，通过不断优化度量指标进行社区发现，代表性算法是Louvain算法［28］；基于标签传播策略的方法先把每个节点的标签传播给它的邻居节点，然后该节点获取邻居节点的标签从而更新自身标签，重复上述标签传播过程，最后各节点根据标签获得所属社区，代表性算法是LPA（Label Propagation Algorithm）［29］。

1.3　社区演化事件识别

社区演化事件识别旨在找出两个相邻快照上社区之间的演化关系。GED（Group Evolution Discovery）模型［30］中定义归属度用于衡量相邻快照上两个社区的相似性，归属度考虑公共节点的数量及其在网络中的位置。GED模型根据相似性结果和社区规模定义7种社区演化事件，包括持续、缩小、扩大、分裂、合并、消失和生成。

2 问题描述

2.1　基本术语

时间片划分点：为动态网络建立快照的每个时刻称为一个时间片划分点。两个相邻时间片划分点决定一个时间片的长度。因此，时间片划分结果可以表示为一系列时间片划分点的集合。

社区改变阈值：最近时间片划分点与当前检查时刻之间社区改变程度的上限。当社区改变程度超过时，将当前检查时刻作为新的时间片划分点。

2.2　非均匀时间片划分问题

3 非均匀时间片划分方法

3.1　主要思想

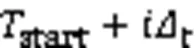
3.2　非均匀时间片划分方法概述

算法1 基于社区改变量估计的非均匀时间片划分。

输出。

4） forfrom 1 todo

11） end if

12） end for

13） return

算法1中包含三个重要函数：第一个函数是Louvain，用于在给定的网络快照上进行社区发现，以找出全部社区，具体算法可参考文献［28］；第二个函数是Modularity，利用模块度评价所找到社区结果的质量，具体计算方式可参考文献［32］；第三个函数是ARIMAForecast，基于时间序列分析模型ARIMA进行模块度预测。3.3节将重点描述ARIMA预测模型的训练方法。

3.3　模块度预测模型训练方法

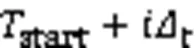
基于算法2获取的训练数据集，确定ARIMA预测模型的参数：、和。参数是模型中的滞后观测数；参数表示确保模块度时序数据平稳所需的差分阶数；参数是移动平均窗口的大小。本文通过实验选择ARIMA预测模型的最佳参数。

算法2 获取训练集数据。

输出 社区模块度值的时间序列。

3） forfrom 0 todo

8） end for

9） return

基于训练数据集和模型参数、和，获得ARIMA模块度预测模型。模型公式如下：

3.4　时间复杂度分析

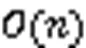
4 实验与结果分析

4.1　实验环境

所有实验均在配置为Intel Core i5-10210U处理器、16 GB RAM、Windows 10（64 bit）操作系统的计算机上进行。本文采用Python 3.7.8实现了基于多种时间片划分方法的社区演化分析系统。

社区演化分析系统由三个组件组成：时间片划分组件、社区发现组件和演化事件识别组件。时间片划分组件以动态网络为输入，时间片划分点为输出，使用三个时间片划分方法生成时间片划分点，即基于社区改变量估计的非均匀时间片划分方法、均匀时间片划分方法和基于网络拓扑改变量的非均匀时间片划分方法；社区发现组件首先根据时间片划分点生成网络快照，然后使用Louvain算法对每个快照进行社区发现；演化事件识别组件采用GED模型，通过比较每两个相邻快照上的社区识别社区演化事件。

4.2　数据集

为验证本文方法的有效性，利用两个真实的公开数据集对传统方法和本文方法进行比较。数据集描述如表1所示，其中：Arxiv HEP-PH数据集［33］是由1993年至2003年期间发表的高能物理现象学（理论）论文形成的引文网络，节点表示发表的论文，边代表论文之间的引用关系；Sx‑MathOverflow数据集［34］是StackExchange网站mathflow上2009年至2016年的时间交互网络，节点表示用户，边表示用户之间的交互关系。

表 1　数据集描述

4.3　对比方法与评价指标

将本文方法与以下两个传统时间片划分方法进行比较。

1）均匀时间片划分方法。采用固定时间窗口长度将动态网络数据离散化为若干个网络快照。

2）基于网络拓扑改变量的非均匀时间片划分方法（简称为基于网络拓扑改变量的划分方法）。利用动态网络变化前后边集的Jaccard系数［19］计算网络拓扑的改变量，当网络拓扑改变量超过预先设置的阈值时生成一个新的时间片，最后获得时间片划分结果。

4.4　实验结果

4.4.1三种时间片划分方法的性能对比结果

基于所实现的社区演化分析系统，分别采用三种时间片划分方法对两种动态网络数据集进行社区演化分析，然后计算评价指标完成时间片划分方法的比较。实验目的是验证基于社区改变量估计的非均匀时间片划分方法的优越性。

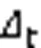
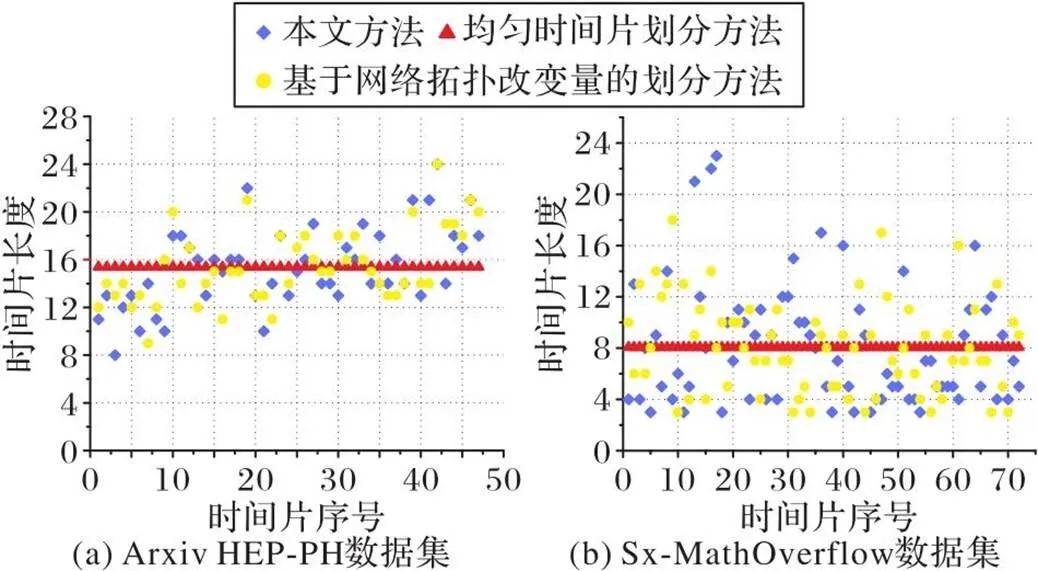
图 1　两个数据集上三种时间片划分方法划分的时间片的长度分布

由表2可以看出，本文方法能够比其他两种方法更及时地识别社区消失事件、更及时地识别社区生成事件，以及可以发现最多数量的社区扩大和社区缩小事件。经分析认为：在动态网络演化过程中，社区的演化与时间呈非线性关系，均匀时间片划分容易错过重要的社区演化事件，最终导致不准确的社区演化分析结果；同时，社区的演化与网络拓扑改变量也呈非线性关系，比如有时删除或添加大量边，社区结构仍旧保持不变，而有时删除或添加少量边就会导致社区结构发生较大变化，因此，基于网络拓扑改变量的划分方法也会降低社区演化分析结果的准确性。本文方法通过直接估计社区的改变量决定何时划分时间片，从而得到更加准确的社区演化分析结果。

表 2　两个数据集上三种时间片划分方法的准确性对比

图2显示了Arxiv HEP-PH数据集中1995年4月30日网络快照的一部分。图中虚线框内的节点表示该快照上的一个社区。基于本文所提出时间片划分方法的社区演化分析结果表明，该社区消失的日期是1995年5月11日；但使用其他两种时间片划分方法情况下，社区演化分析结果中该社区消失的日期分别是1995年5月12日和1995年5月15日。

图 2　1995年4月30日网络快照上的一个社区

图3显示了在Arxiv HEP-PH数据集中1995年6月1日网络快照的一部分。图中虚线框内的节点表示该快照上的一个社区。基于本文所提出时间片划分方法的社区演化分析结果表明，该社区形成的日期是1995年6月1日；但使用其他两种时间片划分方法情况下，社区演化分析结果中该社区生成的日期分别是1995年6月8日和1995年6月18日。

4.4.2社区发现算法对本文方法性能的影响

为了直观验证社区发现方法对所提方法性能影响的程度，以增量式社区发现方法DynaMo［35］和Louvain方法为例，验证所提方法的执行结果，其中均设置为0.02，实验结果如表3所示。

通过实验发现，增量式社区发现方法DynaMo一般比Louvain方法得到的Modularity值低平均5%，即两种社区发现方法下的Modularity几乎相同，实验结果表明社区发现方法对本文所提方法的影响较小。原因分析认为，所有社区发现方法的目的是找到拓扑图中存在的社区，在这些社区中，同一社区内节点之间关系紧密，而社区之间节点关系稀疏。基于社区发现的目的，增量式社区发现方法DynaMo和Louvain方法的社区划分结果是近乎相同的。在拓扑图中社区划分近乎相同，它的Modularity也是近乎相同的，因此社区发现方法对本文所提方法的影响很小。

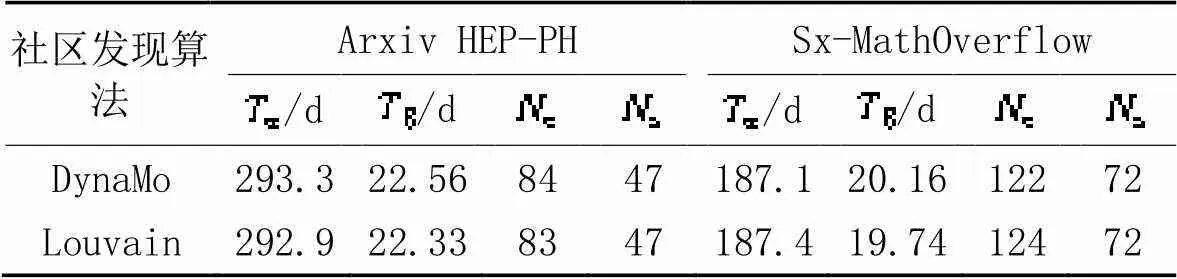
表3　社区发现算法对本文方法性能的影响

4.4.3社区改变阈值对本文方法性能的影响

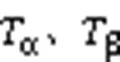
表4　阈值θ对本文方法性能的影响

5 结语

为了提高社区演化分析结果的准确性，本文提出一种基于社区改变量估计的非均匀时间片划分方法。该方法基于时间序列分析模型来预测网络更新后正确社区划分下期望获得的模块度，通过求解该模块度值与保持原有社区划分情况下可获得的模块度之差来估计网络更新后社区改变的程度，一旦社区改变程度超过某个阈值，就会生成一个新的时间片。真实网络数据集上的实验结果表明，本文方法优于均匀时间片划分方法和基于网络拓扑变化量的非均匀时间片划分方法。在相同数量的时间片情况下，本文方法能够更及时地识别社区形成和社区消失事件，并发现更多数量的社区缩小和社区扩大事件，有效提高社区演化分析结果的准确性。

[1] YAN J， LIU G. Two-stage anomaly detection algorithm via dynamic community evolution in temporal graph［J］. Applied Intelligence， 2022， 52（11）： 12222-12240.

[2] JIA X， LI X， DU N， et al. Tracking community consistency in dynamic networks： an influence-based approach［J］. IEEE Transactions on Knowledge and Data Engineering， 2019， 33（2）： 782-795.

[3] PENG H， LI J， SONG Y， et al. Streaming social event detection and evolution discovery in heterogeneous information networks［J］. ACM Transactions on Knowledge Discovery from Data， 2021， 15（5）： No.89.

[4] HU Y， YANG B， LV C. A local dynamic method for tracking communities and their evolution in dynamic networks［J］. Knowledge-Based Systems， 2016， 110： 176-190.

[5] SUN P G， QUAN Y N， MIAO Q G， et al. Identifying influential genes in protein-protein interaction networks［J］. Information Sciences， 2018， 454/455： 229-241.

[6] FREILICH R， ARHAR T， ABRAMS J L， et al. Protein-protein interactions in the molecular chaperone network［J］. Accounts of Chemical Research， 2018， 51（4）： 940-949.

[7] LUO Y， MA J. The influence of positive news on rumor spreading in social networks with scale-free characteristics［J］. International Journal of Modern Physics C， 2018， 29（9）： No.1850078.

[8] JIA J， WU W. A rumor transmission model with incubation in social networks［J］. Physica A： Statistical Mechanics and its Applications， 2018， 491： 453-462.

[9] 陈小强，周丽华，程超，等. 动态网络中稳定社区发现［J］. 小型微型计算机系统， 2015， 36（9）： 1977-1981.（CHEN X Q， ZHOU L H， CHENG C， et al. Detecting stable communities in dynamic networks［J］. Journal of Chinese Computer Systems， 2015， 36（9）： 1977-1981.）

[10] DAKICHE N， TAYEBA F B S， SLIMANI Y， et al. Tracking community evolution in social networks： a survey［J］. Information Processing and Management， 2019， 56（3）： 1084-1102.

[11] TAJEUNA E G， BOUGUESSA M， WANG S. Modeling and predicting community structure changes in time-evolving social networks［J］. IEEE Transactions on Knowledge and Data Engineering， 2018， 31（6）： 1166-1180.

[12] SAGANOWSKI S， BRÓDKA P， KAZIENKO P. Influence of the dynamic social network timeframe type and size on the group evolution discovery［C］// Proceedings of the 2012 IEEE/ACM International Conference on Advances in Social Networks Analysis and Mining. Piscataway： IEEE， 2012： 679-683.

[13] KADKHODA MOHAMMADMOSAFERI K， NADERI H. Evolution of communities in dynamic social networks： an efficient map-based approach［J］. Expert Systems with Applications， 2020， 147： No.113221.

[14] PAN Y， ZHANG L. Modeling and analyzing dynamic social networks for behavioral pattern discovery in collaborative design［J］. Advanced Engineering Informatics， 2022， 54： No.101758.

[15] GUO C， WANG J， ZHANG Z. Evolutionary community structure discovery in dynamic weighted networks［J］. Physica A： Statistical Mechanics and its Applications， 2014， 413： 565-576.

[16] LI W， ZHU H， LI S， et al. Evolutionary community discovery in dynamic social networks via resistance distance［J］. Expert Systems with Applications， 2021， 171： No.114536.

[17] ORMAN G K， ÇOLAK S. Similarity based compression ratio for dynamic network modelling［C］// Proceedings of the IEEE 19th International Conference on Smart Technologies. Piscataway： IEEE， 2021： 227-232.

[18] SULO R， BERGER-WOLF T， GROSSMAN R. Meaningful selection of temporal resolution for dynamic networks［C］// Proceedings of the 8th Workshop on Mining and Learning with Graphs. New York： ACM， 2010： 127-136.

[19] ROSSETTI G， CAZABET R. Community discovery in dynamic networks： a survey［J］. ACM Computing Surveys， 2018， 51（2）： No.35.

[20] WANG Y， ARCHAMBAULT D， HALEEM H， et al. Nonuniform timeslicing of dynamic graphs based on visual complexity［C］// Proceedings of the 2019 IEEE Visualization Conference. Piscataway： IEEE， 2019： 1-5.

[21] BHAT S Y， ABULAISH M. HOCTracker： tracking the evolution of hierarchical and overlapping communities in dynamic social networks［J］. IEEE Transactions on Knowledge and Data Engineering， 2015， 27（4）： 1019-1031.

[22] WANG Z， LI Z， YUAN G， et al. Tracking the evolution of overlapping communities in dynamic social networks［J］. Knowledge-Based Systems， 2018， 157： 81-97.

[23] QIAO S， HAN N， GAO Y， et al. Dynamic community evolution analysis framework for large-scale complex networks based on strong and weak events［J］. IEEE Transactions on Systems， Man， and Cybernetics： Systems， 2021， 51（10）： 6229-6243.

[24] XU Z， RUI X， HE J， et al. Superspreaders and superblockers based community evolution tracking in dynamic social networks［J］. Knowledge-Based Systems， 2020， 192： No.105377.

[25] ÇOLAK S， ORMAN G K. Aggregating time windows for dynamic network extraction［C］// Proceedings of the 2021 International Conference on Innovations in Intelligent Systems and Applications. Piscataway： IEEE， 2021： 1-6.

[26] ORMAN G K， TÜRE N， BALCISOY S， et al. Finding proper time intervals for dynamic network extraction［J］. Journal of Statistical Mechanics： Theory and Experiment， 2021， 2021（3）： No.033414.

[27] GIRVAN M， NEWMAN M E J. Community structure in social and biological networks［J］. Proceedings of the National Academy of Sciences of the United States of America， 2002， 99（12）： 7821-7826.

[28] BLONDEL V D， GUILLAUME J L， LAMBIOTTE R， et al. Fast unfolding of communities in large networks［J］. Journal of Statistical Mechanics： Theory and Experiment， 2008， 2008（10）： No.P10008.

[29] RAGHAVAN U N， ALBERT R， KUMARA S. Near linear time algorithm to detect community structures in large-scale networks［J］. Physical Review E， Statistical， Nonlinear， and Soft Matter Physics， 2007， 76（3）： No.036106.

[30] BRÓDKA P， SAGANOWSKI S， KAZIENKO P. Tracking group evolution in social networks［C］// Proceedings of the 2011 International Conference on Social Informatics， LNCS 6984. Berlin： Springer， 2011： 316-319.

[31] WHEELWRIGHT S， MAKRIDAKIS S， HYNDMAN R J， Forecasting： Methods and Applications［M］. Hoboken， NJ： John Wiley & Sons， 2008： 335-346.

[32] NEWMAN M E J， GIRVAN M. Finding and evaluating community structure in networks［J］. Physical Review E， Statistical， Nonlinear， and Soft Matter Physics， 2004， 69（2）： No.026113.

[33] LESKOVEC J， KREVL A. High-energy physics citation network［DS/OL］. ［2021-12-15］.http：//snap.stanford.edu/data/cit-HepPh.html.

[34] LESKOVEC J， KREVL A. Math overflow temporal network［DS/OL］. ［2021-12-15］.http：//snap.stanford.edu/data/sx-mathoverflow.html.

[35] ZHUANG D， CHANG J M， LI M. DynaMo： dynamic community detection by incrementally maximizing modularity［J］. IEEE Transactions on Knowledge and Data Engineering， 2021， 33（5）： 1934-1945.

Nonuniform time slicing method based on prediction of community variance

LUO Xiangyu1*， YAN Ke1， LU Yan1， WANG Tian1， XIN Gang2

（1，’，’710054，；2’，’710119，）

Time slicing methods in dynamic networks greatly influence the accuracy of community evolution analysis results. As communities vary nonlinearly with time and network topology， both the existing uniform time slicing method and network topology variance-based nonuniform time slicing method are unsatisfactory in capturing community evolution events. Therefore， a nonuniform time slicing method based on prediction of community variance was proposed， where the community variance is quantitatively described by the difference between the community modularity expected to be achieved by the updated network and the community modularity obtained by directly applying the community detection results of the network before changing. Firstly， the prediction model of community modularity was established on the basis of time series analysis. Secondly， with the established model， the expected community modularity of the updated network was predicted， and the prediction value of community variance was obtained. Finally， once the prediction value surpassed a previously set threshold， a new time slice was generated. Experimental results on two real network datasets show that compared with the traditional uniform time slicing method and the nonuniform time slicing method based on network topology variance， on the dynamic network dataset Arxiv HEP-PH， the proposed method identifies community disappearance events 1.10 days and 1.30 days earlier， respectively， and identifies the community forming events 8.34 days and 3.34 days earlier， respectively， and the total number of identified community shrinking and growing events increased by 10 and 1 respectively. On Sx‑MathOverflow dataset， the proposed method identifies community disappearance events 3.30 days and 1.80 days earlier， and identifies the community forming events 6.41 days and 2.97 days earlier respectively， and the total number of identified community shrinking and growing events increased by 15 and 7， respectively.

dynamic network; time slicing; community evolution; time series analysis; community detection; community modularity

1001-9081（2023）11-3457-07

10.11772/j.issn.1001-9081.2022111736

2022⁃11⁃22；

2023⁃02⁃27；

国家自然科学基金资助项目（12071367）； 陕西省基础研究计划面上项目（2022JM⁃317）。

罗香玉（1984—），女，河北邢台人，副教授，博士，CCF会员，主要研究方向：图计算、复杂网络； 闫克（1994—），男，河南南阳人，硕士研究生，主要研究方向：社区演化分析； 卢琰（1998—），女，河南驻马店人，硕士研究生，主要研究方向：社区演化分析、传播动力学分析； 王甜（1999—），女，陕西宝鸡人，硕士研究生，主要研究方向：社区演化分析、传播动力学分析； 辛刚（1984—），男，陕西宝鸡人，高级工程师，硕士，主要研究方向：机器学习、大数据。

TP391

A

2023⁃03⁃08。

This work is partially supported by National Natural Science Foundation of China （12071367）， Program of Basic Natural Science of Shaanxi Province （2022JM-317）.

LUO Xiangyu， born in 1984， Ph. D.， associate professor. Her research interests include graph computing， complex network.

YAN Ke， born in 1994， M. S. candidate. His research interests include community evolution analysis.

LU Yan， born in 1998， M. S. candidate. Her research interests include community evolution analysis， analysis of spreading dynamics.

WANG Tian， born in 1999， M. S. candidate. Her research interests include community evolution analysis， analysis of spreading dynamics.

XIN Gang， born in 1984， M. S.， senior engineer. His research interests include machine learning， big data.