基于几何关系的跨模型通用扰动生成方法

张济慈，范纯龙，李彩龙，郑学东

基于几何关系的跨模型通用扰动生成方法

张济慈，范纯龙*，李彩龙，郑学东

（沈阳航空航天大学 计算机学院，沈阳 110136）（ ∗ 通信作者电子邮箱FanCHL@sau.edu.cn）

对抗攻击通过在神经网络模型的输入样本上添加经设计的扰动，使模型高置信度地输出错误结果。对抗攻击研究主要针对单一模型应用场景，对多模型的攻击主要通过跨模型迁移攻击来实现，而关于跨模型通用攻击方法的研究很少。通过分析多模型攻击扰动的几何关系，明确了不同模型间对抗方向的正交性和对抗方向与决策边界间的正交性，并据此设计了跨模型通用攻击算法和相应的优化策略。在CIFAR10、SVHN数据集和六种常见神经网络模型上，对所提算法进行了多角度的跨模型对抗攻击验证。实验结果表明，给定实验场景下的算法攻击成功率为1.0，二范数模长不大于0.9，相较于跨模型迁移攻击，所提算法在六种模型上的平均攻击成功率最多提高57%，并且具有更好的通用性。

深度学习；对抗样本生成；对抗攻击；跨模型攻击；分类器

0 引言

对抗攻击的提出，更加凸显了神经网络在实际生活和生产中的安全问题，因此，研究对抗攻击算法，不仅能够理解神经网络的内部机制和脆弱性，还能进一步探索如何提升神经网络的安全性和鲁棒性，对神经网络可解释性的发展也有着重要的意义。

在经典的图像分类领域中，对抗攻击可以根据攻击的场景分为白盒和黑盒算法，二者的区别在于攻击者是否可以获得所攻击模型的详细信息，如网络结构、参数等。现有的一些攻击方法是针对单样本-单模型设计的，如在典型的白盒应用场景中，快速梯度下降法（Fast Gradient Sign Method， FGSM）［1］认为神经网络因为具有线性性质而容易受对抗扰动的影响，采用了一种基于梯度符号进行单步攻击的方法；PGD（Projected Gradient Descent）［2］采用了一种min-max最优化框架，利用多步迭代的方式寻找对抗样本，解决了FGSM可能在极小范围内变化剧烈的复杂非线性模型上，解无法收敛的问题；DeepFool［3］同时考虑了梯度信息和神经网络分类器的函数景观，将对抗扰动的求解从多元仿射分类器推广到多元可微分类器中，这种迭代的贪心策略在实践中取得了不错的效果；CW［4］同时兼顾高攻击成功率和低对抗扰动两个方面，是攻破模型蒸馏防御的有效方法。在黑盒场景中，One pixel［5］针对单模型进行攻击，采用差分进化算法求得最优解，该方法仅改变一个像素点就能使神经网络分类器决策失误；受CW启发，ZOO（Zeroth Order Optimization）［6］采用了一种基于零阶优化的算法，以无导数的方式对梯度进行估计，并对一批坐标进行随机梯度下降，提高了计算效率；NATTACK［7］通过求出对抗样本的空间分布，可以针对一个样本生成无数个对抗样本。

以上单样本-单模型的方法在单模型上表现较好，但没有考虑到样本级别的通用性，即扰动对样本集中大部分样本是通用的。因此研究者们又针对多样本-单模型的场景提出大量的样本通用攻击方法，如UAP（Universal Adversarial Perturbation）［8］以及UAP的改进算法［9-10］，UAP表明了分类器高维决策边界之间的几何相关性，并利用每个样本决策边界的相关性和冗余性得到整个样本集的通用扰动。还有一些数据无关的工作被提出，如FFF（Fast Feature Fool）［11］采用一种数据无关的方法生成目标数据不可知的扰动，证明了对网络中单个层的特征激活进行改变就可以改变分类的结果；AAA（Ask， Acquire， and Attack）［12］通过引入生成对抗网络计算通用扰动。

以上研究在样本级别上考虑充分，但都只考虑了单模型。目前针对多模型的研究主要集中在对抗样本的迁移性上，它衡量了一个模型生成的对抗样本在另一个模型上的表现。文献［13］中利用局部平滑梯度代替传统梯度，提出了一个方差减小攻击来提高对抗样本的迁移性；文献［14］中通过结合生成对抗网络进行对抗攻击；文献［15］中通过调整输入的多样性提高迁移成功率；文献［16］中通过结合优化方法和数据增强来提高对抗样本的迁移性，具体是利用Nesterov算法跳出局部最优解，同时加入缩放不变性；文献［17］中对基于动量的攻击进行改进，不仅考虑了图像时域的梯度，还考虑了图像空间域的梯度，获得了较好的迁移成功率；文献［18］的研究考虑了前一次迭代的梯度方差，通过方差调整当前梯度，从而稳定更新方向，提高对抗样本的迁移性。也有部分研究深入探索了对抗样本具有迁移性的内在机制，如文献［19］中通过大量实验对神经网络模型的决策边界和几何特性进行分析，发现不同模型之间梯度方向是近似正交的；文献［20］的研究从类感知的可转移性进行分析，认为对抗样本使不同模型出现相同错误和不同错误的原因是对非鲁棒性特征的使用方式不同。

这些针对对抗样本迁移性的研究取得了大量的优秀成果，但实质上还是没有针对多模型进行攻击，这就意味着这些方法仅针对单样本-单模型或者多样本-单模型。尽管这些研究在单模型上有着优异的效果，但当场景转换为多模型时，这些方法的攻击效率并不能得到保证。在图像分类领域中，跨模型攻击的研究还较少，其中文献［21］中提出了一种集成机制，能保证非目标攻击的成功率，但它攻击成功的评价标准并不是扰动同时在多个模型上生效，因此并不是完全意义上的跨模型通用攻击；文献［22］中设计一种自适应模型权重的方法在集成模型中进行部分像素攻击，对扰动模长和模型的组合权重进行自适应选择，但是实验的分析和评价指标略有欠缺。从目前的研究现状来看，跨模型通用攻击还有很多细节值得探索。

综上所述，本文将研究重点放在单样本-多模型的对抗样本生成方法上。根据两个几何特性，提出了一种基于几何关系的维度累加跨模型通用白盒攻击算法，并提出对抗样本的二范数模长优化方法，实验结果表明，本文算法可以有效地解决跨模型通用攻击问题，并在攻击成功率和效率方面均取得了良好的效果。本文的主要工作如下：

1）分析了不同模型间对抗性方向的关系和对抗性方向与决策边界间的关系，得到两个几何特性结论，证明了跨模型通用攻击的可解性；

2）提出基于几何关系的维度累加跨模型通用攻击方法，利用样本点到决策边界的最短距离确定单模型扰动向量，从多角度验证方法在多模型上的有效性；

3）提出基于二分搜索策略的扰动二范数模长优化方法，可以有效地降低扰动的二范数模长大小，并保证扰动仍是跨模型通用的。

1 跨模型攻击方法

1.1　问题描述

根据式（3），跨模型通用攻击成功的评价指标是所施加的扰动必须在多模型上同时生效，显然，这个问题在多个深度神经网络中是高度复杂的，需要更深入地研究对抗样本的本质以及神经网络模型的性质。

文献［16］的研究发现，不同模型之间梯度方向是近似正交的，此外，文献［23-24］的研究从两种角度诠释了对抗样本存在的原因，其中文献［23］构建了一种更容易被人类理解的方法，从特征的鲁棒性与非鲁棒性出发，提出了对抗扰动是一种特征的本质；文献［24］则从几何流形的角度分析对抗样本的特性，文中提到的流形数据与非流形数据与鲁棒和非鲁棒特征是理解问题的两种不同角度，这两篇文章都对对抗样本的内在特性进行了深入解读。

受上述研究的启发，本文设计了一种基于几何关系的维度累加白盒方法解决跨模型通用攻击问题。该方法集成了不同模型的敏感扰动，使最终的扰动包含多个模型的扰动特性。

1.2　两个几何特性

1）对抗扰动与模型边界的关系。如图1（a）所示，对于一个二元线性分类器，沿着梯度的方向可以以最快速度找到对抗性扰动，最小的扰动可以用式（4）表示，直观的理解就是样本点到决策平面的距离。

在非线性的情况下，根据神经网络决策边界近似线性性质，同样可以通过样本点到决策平面的距离得到对抗性扰动的方向和大小。这与文献［24］中对样本点和决策边界的分析一致，该文中通过凹槽流形解释对抗样本的内在性质及其存在的原因，作者认为训练好的神经网络通过在图像流形中引入凹槽形成了神经网络的决策边界，而样本的对抗性方向近似垂直于图像流形。通过该理论解释和图1（b）中直观的几何关系，可以推断出在一个逼近复杂非线性关系的神经网络模型中，一个样本点的梯度方向即对抗性方向，垂直于该点的决策边界。

图1　二元线性分类器和二元非线性分类器下的对抗扰动求解

不同训练方式下的同种模型（NiN模型）的对抗性方向夹角值如图3所示，可以看出，模型之间的对抗性方向的夹角范围在76°～90°，在这种情况下，本文方法依然可以找到跨模型扰动的可行解，因为将扰动叠加之后，仍然可以保证最终的扰动中包含其他模型的扰动特性。

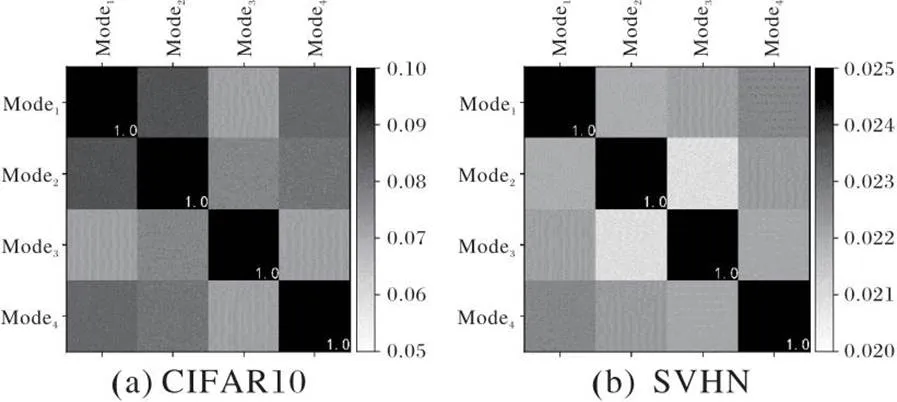
图3　不同训练方式下同种模型（NiN）的对抗性方向夹角值

1.3　线性分类器下的跨模型通用攻击

根据1.2节的描述，可以推出两个有关几何特性的结论：

结论1 在单个模型中，一个样本点的对抗性方向与决策边界近似正交。

结论2 在多个模型中，模型间的对抗性方向即梯度方向近似正交。

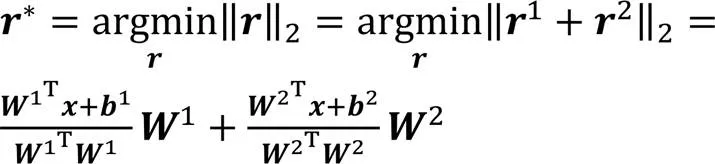
图4　跨两个二元线性分类器的对抗扰动求解

图5　跨三个二元线性分类器的对抗扰动求解

2 跨模型的通用对抗样本生成算法

2.1　非线性分类器下的跨模型通用攻击

前面分析了线性分类器中跨模型通用对抗样本的可解性，根据神经网络局部决策边界近似线性这一依据，将多维线性分类器中扰动生成的思想进一步向深度神经网络的非线性场景中推广，可以得出一个跨模型通用攻击的可行策略。

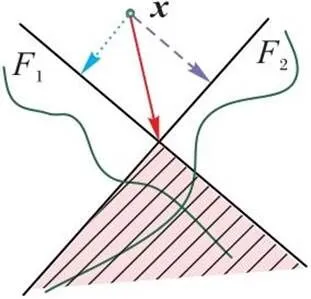
图6　跨两个二元非线性分类器的对抗扰动求解

2.2　跨模型通用攻击算法原理

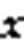
算法1 候选扰动算法。

8） end if

9） end for

算法1中的new_deepfool算法的输入为待攻击样本、攻击模型和已攻击过的标签列表，它与原DeepFool算法的区别是不会再次攻击之前攻击过的标签，这就保证了它不会在原始攻击点和当前攻击点之间停留，而是继续向前寻找下一个可能存在的对抗样本。该算法的攻击原理与DeepFool相同，都是通过迭代地找到将输入图像推向分类模型的决策边界的最小扰动量来工作，该扰动是在最接近决策边界的方向上添加的，然后重复该过程直到图像被错误分类。

算法2 跨模型对抗样本生成算法。

13） end for

14） end for

15） end for

2.3　扰动模长优化

前面具体描述了跨模型的通用攻击方法，为了提高生成的对抗样本的图像质量，设计了二分模长缩减算法对扰动的二范数模长进行优化。

图7　跨模型扰动与跨模型决策边界关系

3 实验与结果分析

3.1　实验设置

本文选用CIFAR10［26］和SVHN［27］数据集，以及NiN［28］、VGG11［29］、ResNet18［30］、DenseNet121［31］、GoogleNet［32］、MobileNet［33］六种典型神经网络分类器，每个分类器通过设置不同的网络参数初始化方式和学习率得到24种神经网络分类器，具体可以分为四种训练方式：方式1（Kaiming初始化+学习率1）；方式2（Kaiming初始化+学习率2）；方式3（Xavier初始化+学习率1）；方式4（Xavier初始化+学习率2）。从测试集中随机选取了1 000张图片进行对抗攻击实验，对本文算法的有效性及性能进行了验证。所有实验均在一台搭载NVIDIA GeForce RTX 2080Ti GPU 的 Linux 工作站上完成，算法采用Python3.8开发环境及PyTorch1.6框架编程实现。

3.2　评价指标

为验证本文攻击算法的效果和性能，设置了如下几个指标，分别为攻击成功率、二范数平均模长、图像质量评估。

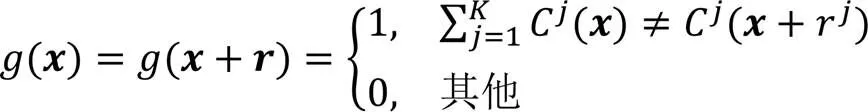
3）图像质量评估指标。

b）峰值信噪比（Peak Signal-to-Noise Ratio， PSNR）是一种评价图像的客观标准，它的值越大，说明失真越少。

3.3　性能验证

为了验证设计算法的攻击质量，从CIFAR10、SVHN测试集中随机抽取1 000个样本进行性能测试，实验分别从两个方面进行测试：第一个方面是采用不同训练方式下的同种模型（模型共4个，具体见表1，每一行为一个模型组）的算法性能；第二个方面是同种训练方式的不同模型（模型共6个，具体见表1，每一列为一个模型组）的算法性能，对比算法选择旨在提高对抗样本迁移性的SINIFGSM［16］、VMIFGSM［18］和VNIFGSM［18］，这些算法在跨模型迁移攻击中表现良好。

表1　模型训练方式

具体结果见表2、3，从第一个方面（表2）可以看出无论是CIFAR10还是SVHN数据集，算法的攻击成功率都是1.0，且生成的对抗样本图像质量良好；从第二个方面（表3）看，无论是在CIFAR10还是SVHN数据集中，算法的跨模型攻击成功率也同样为1.0，生成的对抗样本图像质量良好；无论从哪个方面来看，生成的对抗样本图像质量良好，二范数模长均不大于0.9；SVHN的扰动二范数模长和平均样本迭代次数均略大于CIFAR10数据集，其中采用Kaiming初始化方法训练的模型攻击效果更好。以上的实验结果说明，本文算法在有限个不同模型和相同模型之间的跨模型对抗样本生成问题中都有着良好的效果。

对于表2、3中CIFAR10数据集上的表现效果略优于SVHN数据集的结果，可以解释如下：在模型训练中，实验中用到的模型在SVHN数据集上的收敛速度和测试正确率都高于CIFAR10数据集，这意味着SVHN数据集上的预测值更具有鲁棒性，不易被攻击，因此，它的跨模型通用扰动的二范数模长和平均样本迭代次数会高于CIFAR10。图8是算法生成的跨模型对抗样本的二模长范数分布情况，可以看出在CIFAR10上生成的扰动模长更集中于数值较小的区间，相对于CIFAR10，SVHN数据集下的扰动模长分布跨度较大。

表2　算法2在不同种训练方式下的同种模型间跨模型攻击性能

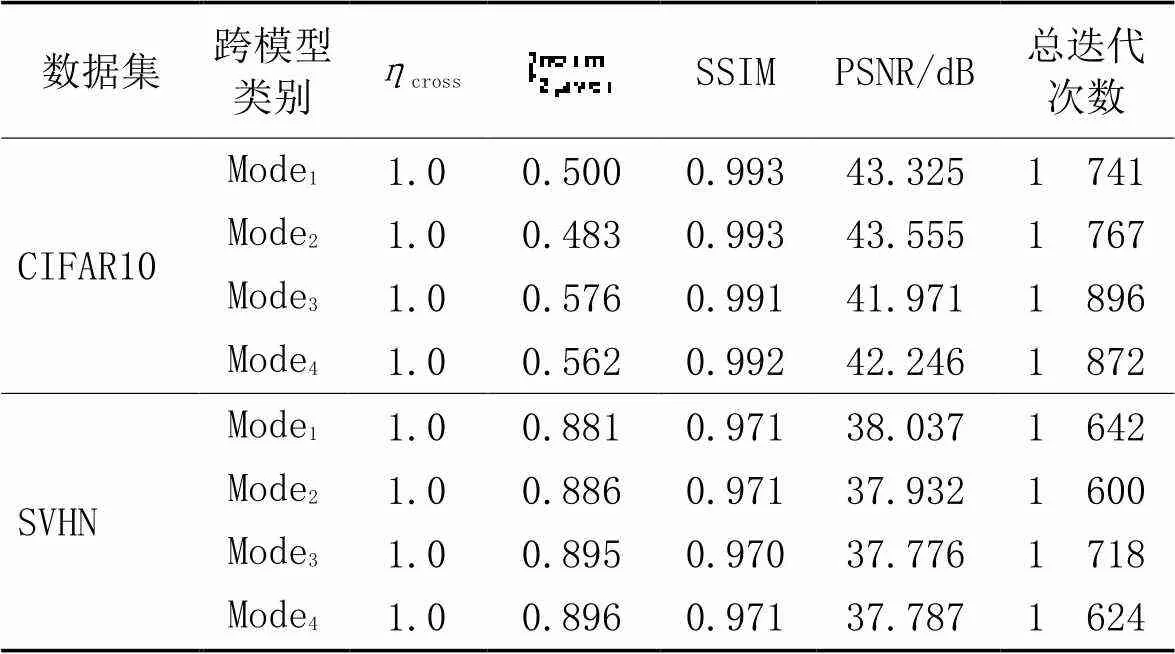
表3　算法2在同种训练方式下的不同模型间跨模型攻击性能

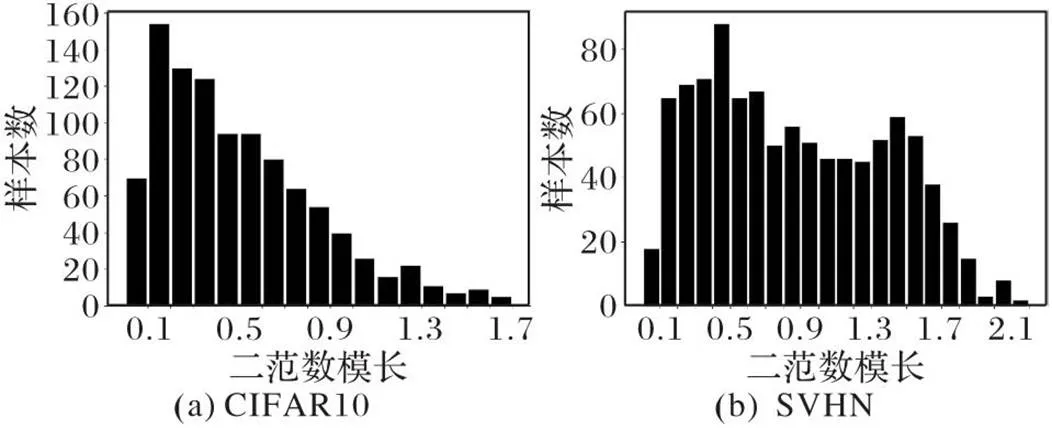
图8　对抗样本模长分布情况

在算法2的基础上加入二分模长缩减策略的攻击质量如表4、5所示，可以看出，加入二分模长搜索策略后攻击成功率仍然与原始性能相当。从跨不同训练方式的相同模型攻击的角度看，在CIFAR10、SVHN数据集中，平均二范数模长下降了10%左右；从跨不同模型攻击的角度看，在CIFAR10数据集中平均二范数模长下降了10%，在SVHN数据集中，平均二范数模长下降了9%；同时，在这两个数据集上，生成的跨模型通用对抗样本的图片质量较之前也有提升，由此可见该策略对于模长的缩减是有效的。

表6显示的是三种对比算法在CIFAR10数据集和六种常见模型（方式1模型组）上的攻击成功率，通过将三种算法在源模型产生的对抗样本迁移到目标模型来获得跨模型迁移成功率，从表中数据可以看出本文算法在攻击成功率上比SINIFGSM、VMIFGSM、VNIFGSM这三种算法都更好，在六种模型上的平均攻击成功率最多提高57%。图9展示了部分对抗样本，从生成的对抗样本质量来看，本文算法相较于对比算法有着更低的人眼敏感度。

表4　模长优化在不同种训练方式下的同种模型间的跨模型攻击性能

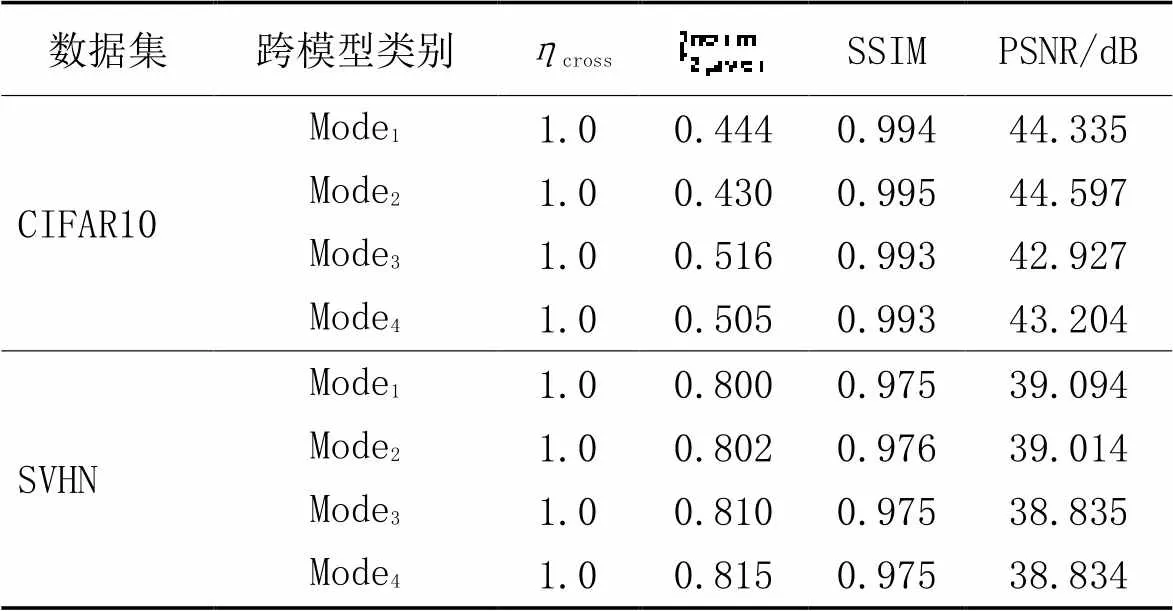
表5　模长优化在同种训练方式下的不同模型间的跨模型攻击性能

图9　对抗样本示例

3.4　结果分析

如图10，实验中发现一个有趣的现象，在CIFAR10数据集上，将每个模型上的分扰动和跨模型扰动分别在模型上的攻击结果进行比较，发现单模型扰动与跨模型扰动的攻击预测标签值在分布上是基本一致的。这说明单模型扰动与跨模型扰动在同一模型上的预测表现基本一致，这一现象可能是由于跨模型扰动是由多个正交的单模型扰动组合而来，这个组合的跨模型扰动保留了多个模型产生扰动的特征，使它可以在多个模型中生效。而在SVHN数据集上，这种现象变得不那么明显，我们推测是SVHN数据集简单、模型的决策边界更鲁棒所导致的。本实验结果表现出来的预测一致性，也可以用非鲁棒性特征［21］解释，即跨模型扰动保留了不同模型最敏感的非鲁棒性特征。

除此之外，还分析了本文算法下的跨模型攻击之间的类别敏感度，图11展示了跨不同模型攻击场景下，模型原始预测类别和算法攻击后的预测类别之间的分布关系。可以看出，在CIFAR10数据集中，原始预测类别到攻击后预测类别的转换有着明显的倾向性，攻击后预测类别为3的样本最多；而在SVHN数据集中，这种倾向性表现为攻击后预测类别为2的样本最多。

表6　对比算法在CIFAR10数据集和六种常见模型上的攻击成功率

注：*表示源模型与目标模型相同。

图10　实验数据集上不同训练方式下的单模型攻击与跨不同模型攻击预测结果对比

4 结语

本文面向跨模型的通用对抗攻击场景，根据模型之间和模型内部的正交性，在DeepFool算法的基础上，提出了一种基于几何关系的跨模型通用攻击方法，并有针对性地提出了一种二分模长优化方法，在保证有效愚弄多个模型的同时，降低了人眼对扰动的可察觉性。

使用CIFAR10、SVHN数据集和NiN、VGG11、ResNet18、DenseNet121、GoogleNet、MobileNet六种典型卷积神经网络模型进行性能验证，实验结果表明本文算法在攻击成功率和二范数模长上都具有很好的效果。但需要指出的是，本文算法在跨模型个数的方面仍有限制，未来工作的一个重要方向是围绕更加通用的跨模型攻击框架展开设计。

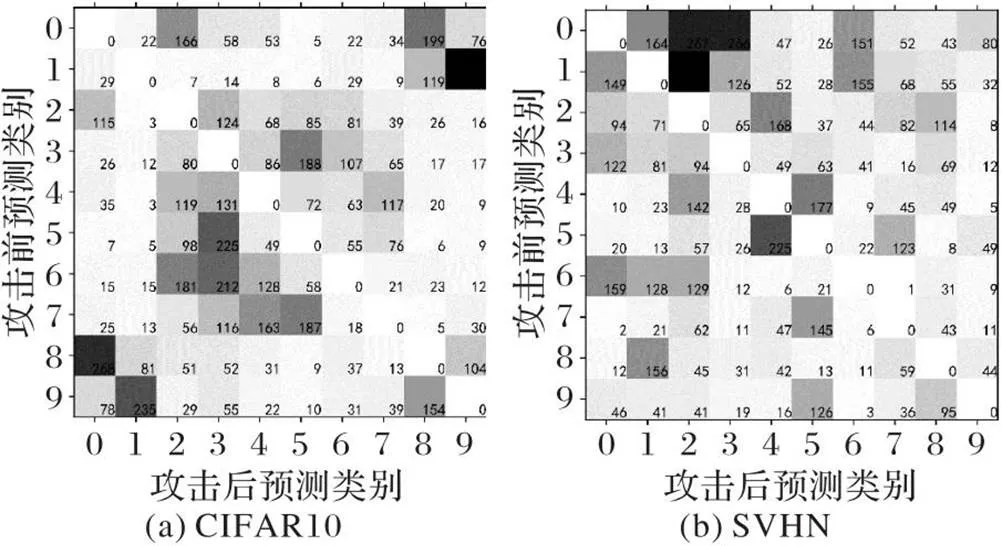
图11　实验数据集上跨不同模型的对抗样本类别敏感度

[1] GOODFELLOW I J， SHLENS J， SZEGEDY C. Explaining and harnessing adversarial examples［EB/OL］. （2015-03-20） ［2022-12-16］.https：//arxiv.org/pdf/1412.6572.pdf.

[2] MĄDRY A， MAKELOV A， SCHMIDT L， et al. Towards deep learning models resistant to adversarial attacks［EB/OL］. （2019-09-04） ［2022-12-16］.https：//arxiv.org/pdf/1706.06083.pdf.

[3] MOOSAVI-DEZFOOLI S M， FAWZI A， FROSSARD P. DeepFool： a simple and accurate method to fool deep neural networks［C］// Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2016： 2574-2582.

[4] CARLINI N， WAGNER D. Towards evaluating the robustness of neural networks［C］// Proceedings of the 2017 IEEE Symposium on Security and Privacy. Piscataway： IEEE， 2017： 39-57.

[5] SU J， VARGAS D V， SAKURAI K. One pixel attack for fooling deep neural networks［J］. IEEE Transactions on Evolutionary Computation， 2019， 23（5）： 828-841.

[6] CHEN P Y， ZHANG H， SHARMA Y， et al. ZOO： zeroth order optimization based black-box attacks to deep neural networks without training substitute models［C］// Proceedings of the 10th ACM Workshop on Artificial Intelligence and Security. New York： ACM， 2017： 15-26.

[7] LI Y， LI L， WANG L， et al. NATTACK： learning the distributions of adversarial examples for an improved black-box attack on deep neural networks［C］// Proceedings of the 36th International Conference on Machine Learning. New York： JMLR.org， 2019： 3866-3876.

[8] MOOSAVI-DEZFOOLI S M， FAWZI A， FAWZI O， et al. Universal adversarial perturbations［C］// Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2017： 86-94.

[9] ZHANG C， BENZ P， IMTIAZ T， et al. CD-UAP： class discriminative universal adversarial perturbation［C］// Proceedings of the 34th AAAI Conference on Artificial Intelligence. Palo Alto， CA： AAAI Press， 2020： 6754-6761.

[10] MOPURI K R， GANESHAN A， BABU R V. Generalizable data-free objective for crafting universal adversarial perturbations［J］. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2019， 41（10）： 2452-2465.

[11] MOPURI K R， GARG U， BABU R V. Fast feature fool： a data independent approach to universal adversarial perturbations［C］// Proceedings of the 2017 British Machine Vision Conference. Durham： BMVA Press， 2017： No.30.

[12] MOPURI K R， UPPALA P K， BABU R V. Ask， acquire， and attack： data-free UAP generation using class impressions［C］// Proceedings of the 2018 European Conference on Computer Vision， LNCS 11213. Cham： Springer， 2018： 20-35.

[13] WU L， ZHU Z， TAI C， et al. Understanding and enhancing the transferability of adversarial examples［EB/OL］. （2018-02-27） ［2022-12-16］.https：//arxiv.org/pdf/1802.09707.pdf.

[14] LI Y， ZHANG Y， ZHANG R， et al. Generative transferable adversarial attack［C］// Proceedings of the 3rd International Conference on Video and Image Processing. New York： ACM， 2019： 84-89.

[15] XIE C， ZHANG Z， ZHOU Y， et al. Improving transferability of adversarial examples with input diversity［C］// Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2019： 2725-2734.

[16] LIN J， SONG C， HE K， et al. Nesterov accelerated gradient and scale invariance for adversarial attacks［EB/OL］. ［2022-12-16］.https：//arxiv.org/pdf/1908.06281.pdf.

[17] WANG G， YAN H， WEI X. Improving adversarial transferability with spatial momentum［EB/OL］. ［2022-12-16］.https：//arxiv.org/pdf/2203.13479.pdf.

[18] WANG X， HE K. Enhancing the transferability of adversarial attacks through variance tuning［C］// Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2021：1924-1933.

[19] LIU Y， CHEN X， LIU C， et al. Delving into transferable adversarial examples and black-box attacks［EB/OL］. ［2022-12-16］.https：//arxiv.org/pdf/1611.02770.pdf.

[20] WASEDA F， NISHIKAWA S， LE T N， et al. Closer look at the transferability of adversarial examples： how they fool different models differently［C］// Proceedings of the 2023 IEEE/CVF Winter Conference on Applications of Computer Vision. Piscataway： IEEE， 2023： 1360-1368.

[21] HE Z， WANG W， XUAN X， et al. A new ensemble method for concessively targeted multi-model attack［EB/OL］. ［2022-12-16］.https：//arxiv.org/pdf/1912.10833.pdf.

[22] WU F， GAZO R， HAVIAROVA E， et al. Efficient project gradient descent for ensemble adversarial attack［EB/OL］.［2022-12-16］.https：//arxiv.org/pdf/1906.03333.pdf.

[23] ILYAS A， SANTURKAR S， TSIPRAS D， et al. Adversarial examples are not bugs， they are features［C］// Proceedings of the 33rd International Conference on Neural Information Processing Systems. Red Hook， NY： Curran Associates Inc.， 2019： 125-136.

[24] SHAMIR A， MELAMED O， BenSHMUEL O. The dimpled manifold model of adversarial examples in machine learning［EB/OL］. ［2022-12-16］.https：//arxiv.org/pdf/2106.10151.pdf.

[25] KNUTH D E. The Art of Computer Programming： Volume 3， Sorting and Searching［M］. Reading， MA： Addison Wesley， 1973.

[26] KRIZHEVSKY A. Learning multiple layers of features from tiny images［R/OL］. ［2022-12-16］.https：//www.cs.toronto.edu/～kriz/learning-features-2009-TR.pdf.

[27] NETZER Y， WANG T， COATES A， et al. Reading digits in natural images with unsupervised feature learning［EB/OL］. ［2022-12-16］.http：//ufldl.stanford.edu/housenumbers/nips2011_housenumbers.pdf.

[28] LIN M， CHEN Q， YAN S. Network in network［EB/OL］. ［2022-12-16］.https：//arxiv.org/pdf/1312.4400.pdf.

[29] SIMONYAN K， ZISSERMAN A. Very deep convolutional networks for large-scale image recognition［EB/OL］. ［2022-12-16］.https：//arxiv.org/pdf/1409.1556.pdf.

[30] HE K， ZHANG X， REN S， et al. Deep residual learning for image recognition［C］// Proceedings of 2016 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2016： 770-778.

[31] HUANG G， LIU Z， MAATEN L van der， et al. Densely connected convolutional networks［C］// Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2017： 2261-2269.

[32] SZEGEDY C， LIU W， JIA Y， et al. Going deeper with convolutions［C］// Proceedings of 2015 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2015： 1-9.

[33] HOWARD A G， ZHU M， CHEN B， et al. MobileNets： efficient convolutional neural networks for mobile vision applications［EB/OL］. ［2022-12-16］.https：//arxiv.org/pdf/1704.04861.pdf.

Cross-model universal perturbation generation method based on geometric relationship

ZHANG Jici， FAN Chunlong*， LI Cailong， ZHENG Xuedong

（，，110136，）

Adversarial attacks add designed perturbations to the input samples of neural network models to make them output wrong results with high confidence. The research on adversarial attacks mainly aim at the application scenarios of a single model， and the attacks on multiple models are mainly realized through cross-model transfer attacks， but there are few studies on universal cross-model attack methods. By analyzing the geometric relationship of multi-model attack perturbations， the orthogonality of the adversarial directions of different models and the orthogonality of the adversarial direction and the decision boundary of a single model were clarified， and the universal cross-model attack algorithm and corresponding optimization strategy were designed accordingly. On CIFAR10， SVHN datasets and six common neural network models， the proposed algorithm was verified by multi-angle cross-model adversarial attacks. Experimental results show that the attack success rate of the algorithm in a given experimental scenario is 1.0， and the L2-norm is not greater than 0.9. Compared with the cross-model transfer attack， the proposed algorithm has the average attack success rate on the six models increased by up to 57% and has better universality.

deep learning; adversarial sample generation; adversarial attack; cross-model attack; classifier

1001-9081（2023）11-3428-08

10.11772/j.issn.1001-9081.2022111677

2022⁃11⁃11；

2023⁃04⁃06；

国家自然科学基金资助项目（61972266）。

张济慈（1998—），女，辽宁海城人，硕士研究生，CCF会员，主要研究方向：深度学习、对抗攻击； 范纯龙（1973—），男，辽宁沈阳人，教授，博士，CCF会员，主要研究方向：神经网络可解释性、复杂网络分析、智能系统验证； 李彩龙（1997—），男，江西上饶人，硕士研究生，主要研究方向：深度学习、对抗攻击； 郑学东（1977—），男，黑龙江五常人，教授，博士，主要研究方向：DNA计算、人工智能。

TP391

A

2023⁃04⁃11。

This work is partially supported by National Natural Science Foundation of China （61972266）.

ZHANG Jici， born in 1998， M. S. candidate. Her research interests include deep learning， adversarial attack.

FAN Chunlong， born in 1973， Ph. D.， professor. His research interests include neural network interpretability， complex network analysis， intelligent system validation.

LI Cailong， born in 1997， M. S. candidate. His research interests include deep learning， adversarial attack.

ZHENG Xuedong， born in 1977， Ph. D.， professor. His research interests include DNA computing， artificial intelligence.