基于振动信号复合特征向量的配电变压器机械故障检测技术研究
2023-11-28刘文昊程胤璋
刘文昊,程胤璋
(1.国网冀北电力超高压分公司,北京 102488;2.国网山西省电力公司电力科学研究院,山西 太原 030001)
0 引言
配电变压器是配电系统中的重要设备,其工作状态直接关系到整个配电网的安全运行。随着高比例新能源和高比例电力电子设备的接入,配电网电源侧与负荷侧波动与不确定性加大,这给配电变压器的安全稳定运行带来了巨大的压力。基于振动信号的配电变压器故障检测方法因其与电力系统无电气连接、操作简单、抗干扰能力强等优势成为近年来故障检测领域的研究热点。基于振动信号的配电变压器故障检测方法最早是由Juan Carlos Burgos等人结合实验数据和仿真模型研究了温度、电流、电压、频率对变压器振动信号的影响,并由此总结得到了一种变压器振动信号的计算模型[1-2]。文献[3]从频域和时域2个方面探讨了变压器型号、容量对振动信号的影响;文献[4]通过实验分析探讨了电力系统中的谐波因素对变压器振动信号的影响。从中可以看出,现有的检测方法往往依据振动信号的单一特征量进行变压器的故障检测,但不同的机械状态可能会引发同一种特征量变化,因此基于单一特征量的检测方法往往会造成误判,而特征量的增加会加重计算机的工作负担,降低计算速度与精度。为了解决上述矛盾,本文提出了基于复合特征向量的配电变压器机械故障检测方案,提高了检测变压器机械故障的效率。
1 配电变压器振动信号与深度置信网络
1.1 变压器振动特性
变压器振动信号是由铁芯、绕组以及冷却装置的振动产生,并通过变压器油和油箱金属结构传递至变压器箱体表面,其流程如图1所示。从图1可以看到,由电动力作用产生的绕组振动经过配电变压器油传递至箱体表面;由磁致伸缩、电磁吸引力产生的铁芯振动通过配电变压器绝缘油、垫脚及紧固螺栓传递至箱体表面;由冷却系统等外围设备运转产生的振动由油箱壁传递至箱体表面[5-6]。

图1 配电变压器振动信号产生及传递示意图
1.2 深度置信网络工作原理
深度置信网络DBN(deep belief network)是一种经典的深度学习算法,具有优异的非线性数据处理能力和自适应特征分析能力。近年来,DBN被广泛用于各种机械设备故障的诊断分析。
DBN是由多个无监督的受限玻尔兹曼机RBM(restricted boltzmann machine)和一个有监督的反向传播网络BP(back propagation)堆叠而成的深度神经网络,拥有强大的特征提取以及数据分类能力[7],其结构如图2所示。由图2可以看到,数据经过DBN网络无监督预训练、有监督微调2个阶段的调整,数据的输入特征就被抽象成更高阶的特征,进而得到更好的分类效果。

图2 DBN网络结构图
2 配电变压器振动信号复合特征向量的提取
本文利用PCB356A16压电式加速度传感器以及NI-9234数据采集仪组成变压器振动信号采集系统,其结构如图3所示。利用采集系统获得的检测结果显示,配电变压器的频率成分以100 Hz及其倍频200 Hz、300 Hz、400 Hz为主。

图3 配电变压器振动信号采集系统
2.1 配电变压器振动信号特征量的提取
获取容量为1 000 kVA的变压器在正常状态与故障状态下的绕组、铁芯振动信号。对采集到的4种类型的变压器振动信号提取特征量,将特征量进行归一化处理。处理后的结果如表1所示。
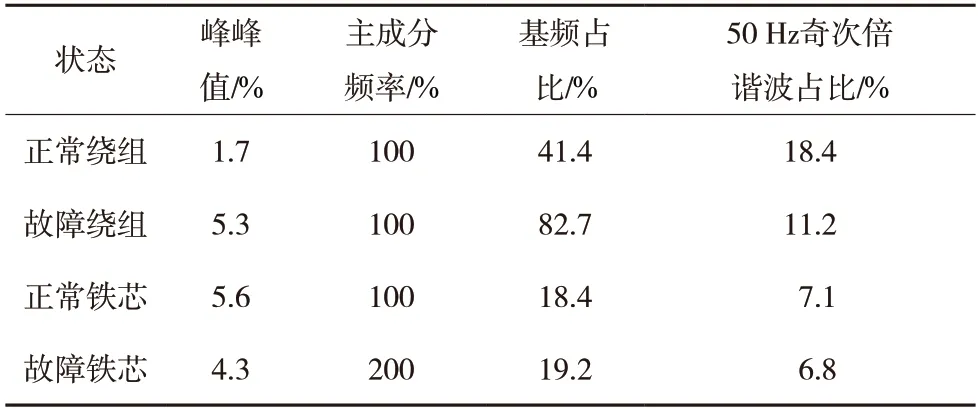
表1 4种类型配电变压器振动信号的特征量
如表1所示,本文以峰峰值、主成分频率、基频占比、50 Hz奇次倍谐波占比为例进行说明,各特征量随配电变压器状态变化而变化,对比每个特征量在各种状态的值,可知不同特征量并不是对每种状态都有着明显的区分度。例如:对于配电变压器正常绕组振动信号、故障绕组振动信号和正常铁芯振动信号,其主成分频率均为100 Hz,而铁芯故障振动信号的主成分频率为200 Hz,这说明主成分频率可以识别出铁芯故障振动信号,而对于其他3种类型的振动信号识别效果较差。本文将单个特征量输入DBN网络中进行分类处理,得到的分类结果如表2所示。

表2 DBN对单个特征量的识别效果
由表2可知,单独使用一种特征量对变压器振动信号类型进行识别时,准确率最高的是基频占比,此时DBN网络对4种类型的振动信号识别准确率为89.3,而单独使用基频作为特征量时,DBN的识别准确率最低为50。由此说明仅使用一种特征量对变压器振动信号进行分类识别时,其准确率较低。
本文从波形和IMF分量能量2个角度进行特征量的提取。在振动信号波形方面,本文选择均值、峰峰值、偏度、峭度、基频、基频占比、50 Hz奇次倍频占比作为特征量。
2.1.1 均值
在配电变压器振动信号中,均值可以表征振动信号的对称程度,正弦波形的均值为零,波形的均值越接近零说明波形的对称性越好,所发生的畸变也越小,变压器状态也越趋于正常。
2.1.2 偏度
偏度是反映数据分布偏斜方向和程度的统计量,可以表征波形相对于平均值的不对称程度。其计算公式为
其中,Skew(x)代表数据偏度;xi代表信号数据;代表信号平均值;代表信号方差。
2.1.3 峰峰值
配电变压器出现铁芯、绕组松动等机械故障时,变压器振动强度变大。峰峰值是指一个周期内信号最大值与最小值之间的差值,可以反映变压器振动强度的大小。其计算公式为
2.1.4 峭度
峭度是描述信号波形尖峰度的数值统计量,可以反映数据的分布特性。峭度一般用K来表示,其计算公式为
其中,E(x-μ)代表数据 x 的期望值;μ代表数据 x 的均值;代表数据 x 的标准差。
由式(4)可知,峭度是一种4阶累积量。不同类型的变压器振动信号,其信号波形的尖峰度也不相同。
2.1.5 基频
现有的研究表明,正常状态下变压器绕组、铁芯的振动信号应该以100 Hz为基频信号,受材料非线性的影响会有少量的100 Hz倍频分量。而当配电变压器发生机械故障时,100 Hz倍频分量的成分会大大增加,进而成为振动基频信号。因此,本文将振动信号的基频信号作为判断变压器机械状态的特征量。
2.1.6 基频占比
基频占比是指信号的频谱中,基频幅值与所有频次幅值总和的比值。配电变压器不同机械状态下,其振动信号的频谱分布规律不同,以基频占比作为表征变压器状态的特征量可以同时反映振动信号中基频与谐波的变化情况。
2.1.7 50 Hz奇次倍频占比
配电变压器振动信号中还存在有50 Hz奇次倍频分量,这是由于变压器结构较为复杂,铁芯、绕组振动信号相互影响所致,该分量在变压器发生机械故障后更加明显。
对一台容量为1 000 kVA的配电变压器进行松动故障设置,以获得其在正常状态与铁芯松动故障的振动信号,计算振动信号以上特征量,得到的结果如表3所示。

表3 故障前后变压器振动信号波形特征量
由表3可知,故障后振动信号的波形特征量都发生了不同程度的变化,说明可以使用以上特征量来检测变压器的机械状态,将以上特征量组成波形特征向量vb。
信号的能量特征也是反映信号类型的重要特征量,不同机械状态下的变压器振动信号具有不同的能量特征,而固有模态函数IMF(intrinsic mode function)分量是由原始振动信号经过经验模态分解EMD(empirical mode decomposition)得到的,所以不同类型振动信号的IMF分量有着不同的能量特征。可以通过分析各个IMF分量的能量值来实现对变压器机械状态的检测[8]。
每个IMF分量的能量计算方法如式(5)所示。
为了简化计算,本文选用每个IMF的2范数来表征其能量特征,计算公式如式(6)所示。
由表4可知,故障后振动信号各IMF分量的能量特征都发生了不同程度的变化,说明可以使用以上特征量来检测变压器的机械故障,将以上特征量组成能量特征向量vn。
振动信号波形特征向量vb与IMF分量能量特征向量vn分别从整体和局部两个角度反映变压器的机械状态,将两者组成复合特征向量VF。
两者互为补充,可以获得较为准确的配电变压器机械状态信息。但这样所组成的特征向量共有14个特征量,维数过高,如果将其直接送入分类器进行状态识别会给计算机带来较大的工作负担和计算误差。
2.2 主成分分析法原理
针对高维数特征向量在机器识别中所面临的问题,本文提出使用主成分分析法的优化方法,既能最大限度地保留原始数据的特征信息,又能使特征向量维数大幅下降,进而减小计算机工作负担,提高运算速度与精度。
假设X=(x1,x2,……,xn)为m×n的原始特征矩阵,其中m表示数据中特征向量个数,n表示数据中特征向量的维数,xi表示第i个m维列向量。
计算x1、x2、xn……的协方差矩阵C:
这样就可以从原始的 n 维特征向量中提取出r维的主成分,从而达到降维的目的。使用主成分分析法既可以较为完整地保留数据的原始信息,又可以达到减少变量、加快计算机运算速度的目的[9-10]。
2.3 基于主成分分析法的配电变压器振动信号复合特征向量
针对综合反映配电变压器振动信号波形特征和能量特征的复合特征向量,使用主成分分析法求其协方差矩阵并提取主成分,所得到的协方差矩阵特征根及其贡献率如表5所示。

表5 协方差矩阵特征根及其贡献率
由表5可知,前两个特征因子所对应的特征根数值较大,两者累计贡献率大于90,可以表达原始特征向量绝大部分的特征信息,因此将这两个特征值作为主成分特征向量代替原有的特征向量进行分析,由此降低了特征向量的维数[11]。
根据以上方法得到的正常状态与故障状态下配电变压器绕组、铁芯振动信号的主成分特征向量如表6所示。

表6 不同类型变压器振动信号的主成分
由表6可知,经过主成分分析法优化的14维复合特征向量被处理成2维主成分特征向量,有利于提高分类器的工作效率。
3 基于复合特征向量的配电变压器机械故障检测
本文根据复合特征向量与DBN网络在故障检测方面的优越性,提出了基于复合特征向量的变压器机械故障检测方法,具体流程如图4所示。首先采集目标变压器振动信号并构建复合特征向量,然后使用主成分分析法对复合特征向量进行优化处理得到主成分特征向量。提取多组已知状态下振动信号主成分特征向量作为DBN网络的训练样本与测试样本,训练样本通过DBN网络两阶段的训练得到特征向量与配电变压器机械状态之间的对应关系,再将其应用于测试样本的分类,得到测试样本的分类结果与准确率。

图4 基于复合特征向量的配电变压器机械故障检测流程图
本文采集配电变压器正常状态铁芯振动信号、故障状态铁芯振动信号、正常状态绕组振动信号、故障状态绕组振动信号4种类型的振动信号,通过主成分分析法对复合特征向量进行优化处理,得到2维主成分特征向量。分别选取主成分分析法优化前后的1 200组数据作为训练样本,200组作为测试样本输入DBN网络进行分类识别,结果如图5所示。
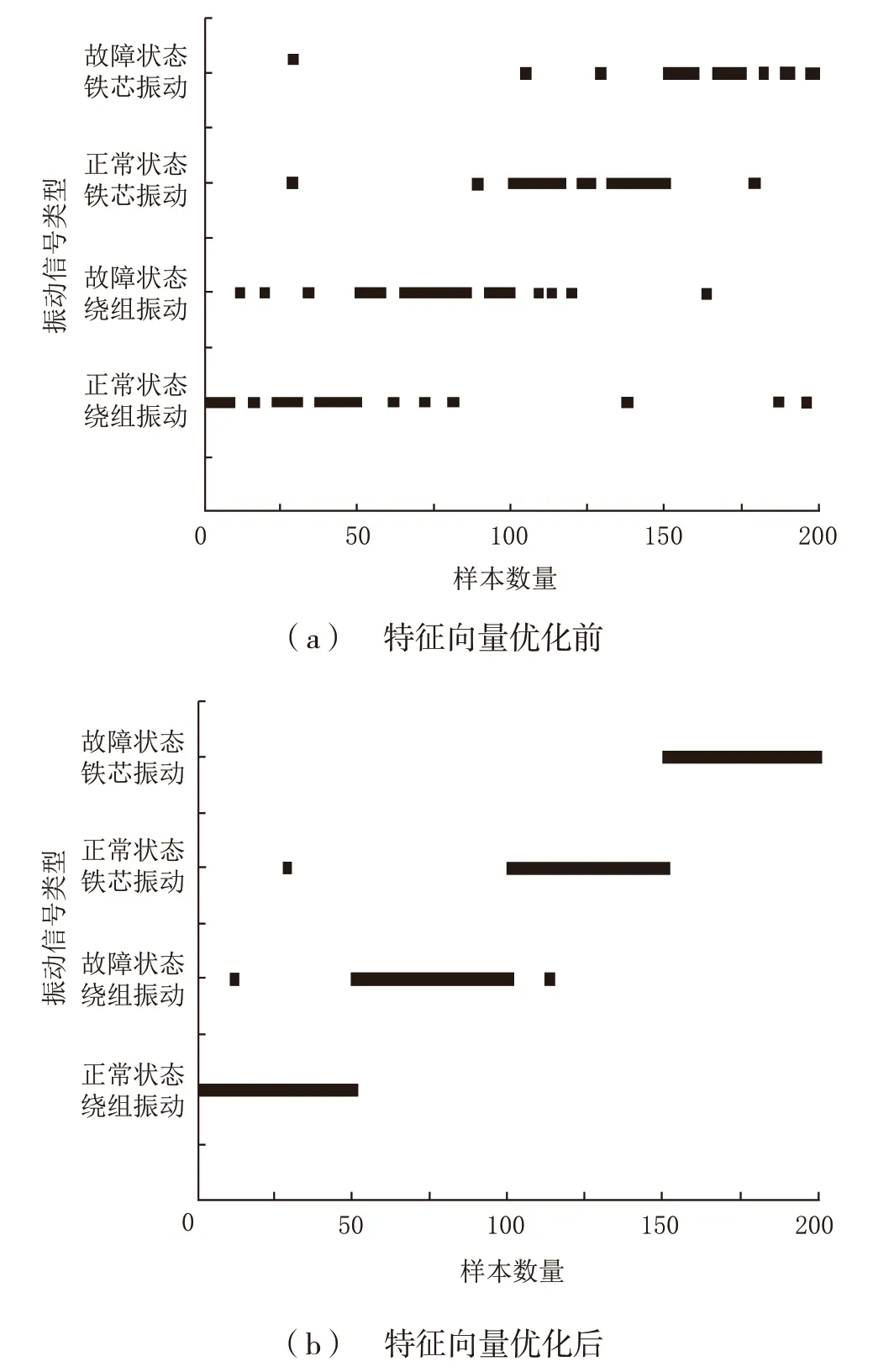
图5 优化前和优化后的DBN识别结果
如图5(a)所示,在特征量优化之前,DBN网络对未优化特征量数据的识别精度为91.0;如图5(b)所示,使用主成分分析法对特征量优化后的DBN分类结果DBN网络的识别精度为98.5。说明主成分特征向量可以很好地保留原始特征向量的信息,减小分类器的工作负荷,提升分类器的识别准确率。
4 结论
本文针对配电变压器振动信号的波形特征和能量特征建立了复合特征向量,结合主成分分析法和DBN网络的特点提出了基于复合特征向量的变压器机械故障检测方法,分析试验数据结果得出了以下结论:
a)振动信号的波形特征量和能量特征量都可以反映变压器机械状态的变化,但使用单一特征量进行变压器机械状态识别通常会引发误判。
b)使用主成分分析法可以在保留原始信息的基础上,有效降低复合特征向量维数,进而提高分类器的工作效率。
c)针对基于复合特征向量的配电变压器机械状态识别,使用DBN网络作为分类器具有比传统BP神经网络更好的识别效果。
d)实验结果说明基于复合特征向量的配电变压器机械故障检测方法可以用于变压器的故障检测。
