电磁过滤器去除热网腐蚀产物数学模型研究与应用

叶 洲，田文华，王园园

（1.福建华电可门发电有限公司，福建 福州 350000；2.西安热工研究院有限公司，陕西 西安 710032）

0 引言

热电联产以能源消耗低、环境污染小、供热成本低等优势随着我国供热需求的迅速增长而快速发展，供热机组的规模化和大型化发展已成为趋势，大型发电机组的供热改造也与日俱增。与此同时，高温高含铁量的热网回水处理问题也引起了电厂化学领域的广泛关注[1]。调研发现，热网系统启动时，热网回水含铁的质量浓度最高可达1 800 μg/L以上。若将其处理达到《火力发电机组及蒸汽动力设备水汽质量标准》（GB/T 12145—2016）中机组的给水标准，就能直接进入除氧器回用于锅炉系统。目前，我国热网回水的处理技术发展很快，其中电磁过滤技术是一种根据物料磁性差异进行分离的技术[2]，以能够耐受高温高压流体、除铁效率高、电耗低、占地面积小等独特优势，在前苏联及日本等国的电站凝结水精处理等领域得到了应用[3]。我国近年来所开发出的新型电磁过滤器，已应用在电厂高温疏水等处理领域[4]。本文通过采用国内某公司设计制造的电磁过滤器试验数据，建立了电磁过滤器去除悬浮铁的数学模型，并根据模型对电磁过滤器运行时的工艺参数进行优化，取得了很好的效果。

1 电磁过滤器数学模型的研究

1.1 数学模型的建立

模型的假设条件如下：

a）水中悬浮铁的成分和颗粒分布不随时间变化而变化。

b）悬浮铁颗粒之间无相互作用。

c）悬浮铁颗粒很小，且形状为球形，其重力和浮力的作用可以忽略。

d）电磁过滤器可以作为推流式反应器来看待。

在运行工况不发生改变的情况下，电厂用水中铁的含量一般较低，水中悬浮铁的成分和分布基本不变，且相互之间作用力很小，假设条件a）和条件b）满足；水中悬浮铁颗粒的粒径很小（均小于100 μm），其重力和浮力很小，可以忽略不计，假设条件c）满足；电磁过滤器的运行流速较高，且过滤通道长宽比大于3，可近似认为电磁过滤器为推流式反应器，假设条件d）满足。

假设条件成立，将电磁过滤器过滤通道分割成无数个微元，微元模型如图1所示。

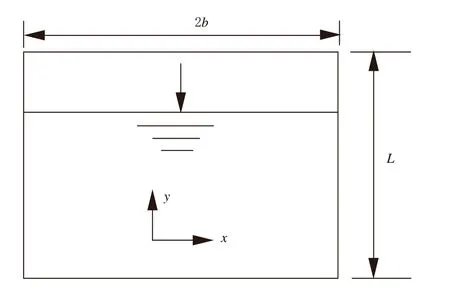
图1 坐标系微元模型图

在忽略了重力和浮力的作用后，同时悬浮铁颗粒相互之间作用力忽略不计，电磁过滤器内部每一个微元内的悬浮铁主要受到x轴方向上电磁力及水体阻力2个力的作用。

a）电磁场作用于悬浮铁颗粒的电磁力[5]：

其中，F为作用于悬浮铁颗粒的磁力；γ为悬浮铁颗粒的磁化率；V为悬浮铁的体积；H为磁场强度；dH/dx为磁场强度梯度。

b）水体作用于悬浮铁颗粒的阻力[6]：

其中，Fz为作用于悬浮铁颗粒的阻力；为阻力系数；v为悬浮铁颗粒相对于过滤通道边界的运动速度；d为悬浮铁颗粒的粒径；ρ为水的密度。

由式（1）和式（2）推导出悬浮铁颗粒在静止水体中的运动方程为

从式（3）可以看出，当颗粒运动速度越来越大时，作用在颗粒的外力将会达到平衡，悬浮铁颗粒加速度为0，此时颗粒将进行匀速运动。因此，由式（3）得

悬浮铁颗粒移动到边界时即视为颗粒被过滤器捕获，由于该过程时间很短，因此可忽略加速过程，直接将v视为颗粒从中心移至边界的速度。根据图1，设水的流速为vs，建立物料守恒公式[7]：单位时间内被吸附到微元边界悬浮铁的量等于单位时间内微元中悬浮铁的减少量，即

其中，b为微元中轴线至通道边界距离；vs为水流流速；V为悬浮铁的质量分数；dy为沿 y 轴的长度微元。

设悬浮铁的初始质量分数为V0。对式（5）两边分别从和0～L积分得

其中，L为过滤通道的长度。由式（6）得

其中，Cis为电磁过滤器进水中悬浮铁的含量；C0s为电磁过滤器出水中悬浮铁的含量。由式（7）得

需要注意的是，在对式（5）进行积分时，包含了一个临界条件：即微元中轴线上的悬浮铁颗粒从微元进口移动至出口的时间刚好等于其从中轴线移动至边界的时间。通过悬浮铁颗粒的受力分析可知，其沿x轴的移动速度是与粒径大小有关的。因此，对于整个过滤器而言，可以认为粒径大于满足边界条件的颗粒将被过滤器截留，而粒径小于满足边界条件的颗粒将会漏过。因此，对于同时过滤的一批粒径不同的悬浮铁，可以将式（4）中的d用de代替：

其中，de满足边界条件的颗粒粒径。将式（9）带入式（8）中可得

其中，Cd为水中溶解铁的含量，μg/L；Ci为进水中全铁的含量，μg/L；C0为出水中全铁的含量，μg/L；K为常数，m/h。式（11）即为电磁过滤器去除水中悬浮铁的数学模型。

1.2 数学模型的检验

电磁过滤器数学模型的研究成果基于理论推导建立，是否具有实际指导作用，则需要通过试验进行验证。

1.2.1 试验条件

a）试验装置。为了验证电磁过滤器的数学模型，本次试验设计了专门的动态实验装置，装置系统如图2所示。动态试验装置主要包括水箱、母液箱、离心泵、计量泵、管道混合器、电磁过滤器和空气反洗设备。整个系统能实现电磁过滤器过滤、水反冲洗、空气擦洗等功能。试验时，通过调整计量泵流量，可将母液箱内的工作液与水箱的进水混合配成含铁量不同的水样。该电磁过滤器为实际工程所用的流量最小的一款设备，运行流量最大可达50 m3/h，试验达到了中试规模。

b）投加的腐蚀产物。本次试验采用某电厂凝结水精处理系统前置过滤器反冲洗水中铁的悬浮物经沉淀、过滤、烘干等工序制备成的铁粉作为电磁过滤器进水中投加的腐蚀产物。采用激光粒度分析仪对该样品进行了粒径分布的测定，结果如表1所示；同时用X射线衍射XRD（X-ray diffraction）检测了该样品的物相组成，结果如表2所示[8]。

表1 悬浮铁的粒径分布

表2 悬浮铁的物相组成分布

c）试验用水。经超滤过滤的自来水，水中溶解态铁的质量浓度为1 μg/L。

1.2.2 测定方法

若铁的质量浓度在10～5 000 μg/L，采用《锅炉用水和冷水分析方法 铁的测定》（GB/T 14427—2017）测定；若铁的质量浓度小于10 μg/L，采用《火力发电厂水、汽试验方法铜、铁的测定 石墨炉原子吸收法》（DL/T 955—2016）测定。

1.2.3 测定仪器

紫外分光光度计（UV-9600型，北京瑞利分析仪器公司），原子吸收光谱仪（Z2000型，日本日立公司）。

1.2.4 试验结果与讨论

根据式（11），K为常数，当水中溶解铁Cd含量一定时，出水含铁量C0只与进水含铁量Ci及过滤流速vs相关。因此，本试验通过改变电磁过滤器的运行参数，验证电磁过滤器的数学模型。

a）保持运行流速vs不变对模型进行验证。

当vs一定时，为常数，Co-Cd与Ci-Cd呈正比关系。试验中，固定流速为190 m/h，通过测定一组不同进水含铁量Ci及相应的一组出水含铁量C0，对试验结果进行一元线性回归分析，得出R2=0.985 7，线性回归结果如图3所示。

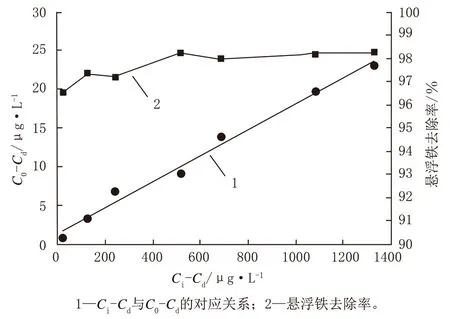
图3 Ci-Cd与C0-Cd的关系和悬浮铁去除率

b）保持进水含铁量Ci不变对模型进行验证。

K为常数，-ln[（C0-Cd）/（Ci-Cd）]与1/vs呈正比关系。试验中，改变过滤流速，同时测定不同流速下电磁过滤器进水（实测值为准）和出水的含铁量，对试验结果进行一元线性回归分析，得出R2=0.988 2。线性回归结果如图4所示。

图4 1/vs与-ln[（C0-Cd）/（Ci-Cd）]的关系和悬浮铁去除率

试验结果表明：运行流速固定为190 m/h时，进水悬浮铁的质量浓度在20～1 300 μg/L范围内，电磁过滤器悬浮铁的去除率维持在98左右，电磁过滤器进水含铁量越大，出水含铁量也相应增大，二者符合式（12）中的关系；电磁过滤器进水含铁量不变时，流速在186～660 m/h范围内，电磁过滤器悬浮铁的去除率随着流速的增加而降低，1/vs与-ln[（C0-Cd）/（Ci-Cd）]符合公式（13）中的线性关系，且低流速运行时有利于提高电磁过滤器的除铁效率。因此，对进水悬浮铁含量Ci和水流速vs两个自变量的检验结果表明，建立的电磁过滤器去除水中悬浮铁的数学模型在进水悬浮铁质量浓度为20～1 300 μg/L，流速为186～660 m/h范围内是正确的，可以用于指导电磁过滤器运行参数的优化及新型电磁过滤器的设计。

2 电磁过滤器数学模型的应用

2.1 电磁过滤器性能常数的定义

电磁过滤器去除水中悬浮铁的数学模型式（11）中，特殊的常数K是表征电磁除铁过滤器性能的重要参数，定义K值的单位为m/h。其表达式为

依据式（14）可知，保持进水含铁量不变时，图4中拟合曲线的斜率即为电磁过滤器的除铁性能常数K。K值越大，表明电磁过滤器除铁能力越强。

2.2 电磁过滤器性能常数的应用

电磁过滤器除铁性能常数K可以用于评价电磁过滤器性能的优劣，也可用于指导用户对电磁过滤器的选型和电磁过滤器的设计。在实际工程应用中，用户所面临的主要问题是需要根据不同的进水条件及出水水质要求来确定电磁过滤器的最佳运行流速，保证电磁过滤器达到最大除铁效率。最佳运行流速的表达式为

例如，本次试验所用的电磁过滤器性能常数K为543 m/h。调研得知某亚临界直流供热机组的热网回水中全铁Ci平均约为28.6 μg/L，溶解铁Cd平均为6.2 μg/L；而按照《火力发电机组及蒸汽动力设备水汽质量》（GB/T 12145—2016）的规定，亚临界直流机组给水含铁质量浓度C0应小于10 μg/L。将上述数值代入式（15）得：vs为306 m/h。

为了保证机组的安全运行，取安全系数为1.3，则试验所用的高梯度电磁过滤器应用于某电厂热网回水的过滤除铁时，其最佳运行流速vs约为235 m/h。

3 结论

在工程应用中，为降低投资及运行成本，需要对电磁过滤器的设计及运行参数进行优化，这就需要首先研究电磁过滤器除铁的规律。在水处理领域，数学模型是描述水处理设备去除污染物规律的最佳方式，应用十分广泛。本文推导的电磁过滤器除铁的数学模型为并通过试验进行了验证，证明该数学模型可以用于指导电磁过滤器的设计、选型和运行优化。