基于SolidWorks“立体表面上点和线”类虚拟模型的创建方法

郗志刚

（佛山科学技术学院机电工程与自动化学院，广东佛山 528225）

工程图样是设计与制（建）造过程中工程与产品信息的载体、表达和传递设计信息的主要媒介，在机械、土木、水利工程等领域的技术与管理工作中有着广泛的应用，被喻为“工程界的语言”［1］。因此，“工程制图”是普通高等学校工科专业重要的工程基础课程，用以培养学生工程图样绘制、阅读以及形象思维能力，具有理论体系严谨、与工程实践联系密切等特点。

作为“八五”、“九五”科技攻关项目，我国在1992 年启动了“CAD 应用工程”［2］。随着二维、三维CAD 技术在工程设计和加工制造领域应用的全面普及和推广，将CAD 技术引入“工程制图”教学也一直是我国图学界的研究热点。特别是伴随着三维CAD 技术的日臻成熟和应用普及，在“工程制图”教学环节中，利用三维几何建模进行各种教学改革的应用实践也在不断深入，方法更是多种多样［2-6］。

在各种教学实践和探索中，应用CAD 软件建立三维虚拟模型，利用虚拟模型立体感强、构建容易、修改方便、信息量大、便于线上共享等优点，丰富了教学手段，增强了学生的空间想象和形象思维能力，成为“工程制图”课程教学改革中的重要应用之一。但在这些教学实践中，主要是单个立体和装配体等虚拟模型的构建，基本没有涉及到展示“立体表面上点和线”的虚拟模型如何创建。立体表面上点和线投影关系的相关知识点，既是后续学习截交线、相贯线、组合体等内容的基础，也是课程学习的难点。目前，随着“混合式教学”、“翻转课堂”等教学模式改革的开展，学生在课外通过信息技术的帮助，完成知识的接受学习也显得越来越重要。由于“立体表面上点和线”虚拟模型的制作方法，与一般的三维建模方法和思路不尽相同，为了便于进行相关知识点的教学实践，本文基于SolidWorks 软件，介绍几种“立体表面上点和线”虚拟模型的创建方法。

1 创建平面立体及其表面上点的虚拟模型

平面立体是由若干个平面图形封闭而成的空间实体，基本体中主要包括棱柱和棱锥。制作平面立体表面上点的虚拟模型，主要目的是直观地体现点的从属性和可见性。

1.1 棱柱表面上点的虚拟模型制作

以图1 所示“求作三棱柱水平投影，并补全表面上点三面投影”［7］为例，介绍一种虚拟模型的制作方法。

图1 棱柱及其表面上的点

（1）按照三棱柱的尺寸，创建三棱柱模型；

（2）使用“草图绘制”工具，将各“点”分别绘制在三棱柱相应的表面上，并通过“几何关系”和标注尺寸，使“点”的位置准确，如图2 所示；

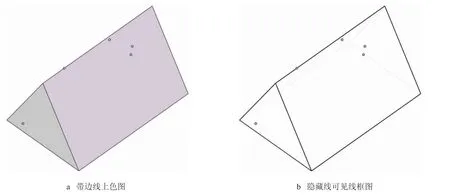
图2 三棱柱及其表面上点的三维模型

（3）新建工程图文档，插入表面带点三棱柱的三个投影和轴测图。当点所在平面的投影具有积聚性时（如B、C 点的侧面投影，D、E 点的水平投影和正面投影），点的投影与面的积聚性投影重叠，相应点的投影显示不出来，需要使用“草图”将不显示的“点”重新绘制，并通过添加“几何关系”和标注尺寸，确保“点”的位置准确。“点”的位置确定后，将标注的尺寸隐藏；

（4）对投影图和轴测图中每个点添加注释（点不可见加括号），如图3 所示。

图3 三棱柱及其表面上点的投影图和轴测图

这种制作方法的优点是简单快捷，表面上的点符合原型；缺点是在投影图中，当点所在面具有积聚性时，点与面的投影重叠，需再次添加。另外，在e-drawing 模型中，表面上的点与面完全融合，观察不到了。

1.2 棱锥表面上点的虚拟模型制作

以图4 所示“求作四棱台侧面投影，并补全表面上点三面投影”［7］为例，介绍第2 种虚拟模型的制作方法。

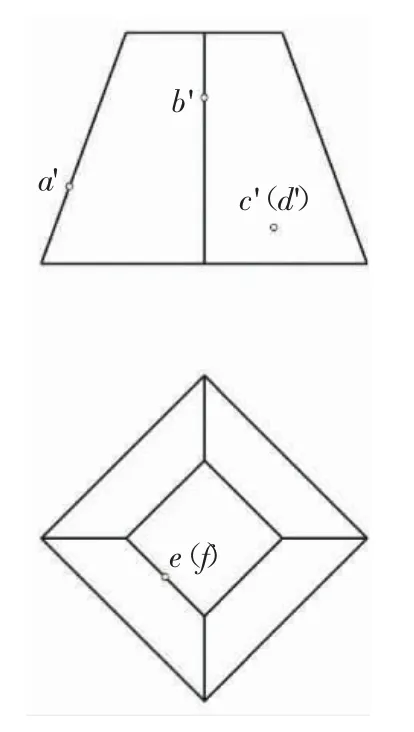
图4 棱锥及其表面上的点

（1）为了使“点”在模型中的直观性比较强，可用一个小圆球表示“点”；为此，先准备一个“圆球”模型，其直径可根据平面立体的大小成比例设定（通常可取直径为1～1.5 mm），并将其单独保存为一个文件；

（2）按照四棱台的尺寸，创建四棱台模型；

（3）使用“插入＞零件”工具，将“点”插入到四棱台中；在插入零件过程中，注意勾选“转移”中的“实体”、“基准面”和“找出零件”选项，以便后续“点”的移动和定位；

（4）利用“重合”、“距离”等配合设定，将“点”准确地放置在立体表面上应有的位置上；

（5）重复以上两个步骤，依次将立体表面上所有的点均插入到四棱台中；

（6）使用“插入＞特征＞组合”工具，将所有插入的“点”与“四棱台”组合为一个实体；

（7）新建工程图文档，插入表面带点的四棱台的3 个视图和轴测图，并对每个点添加注释（点不可见加括号），如图5 所示。

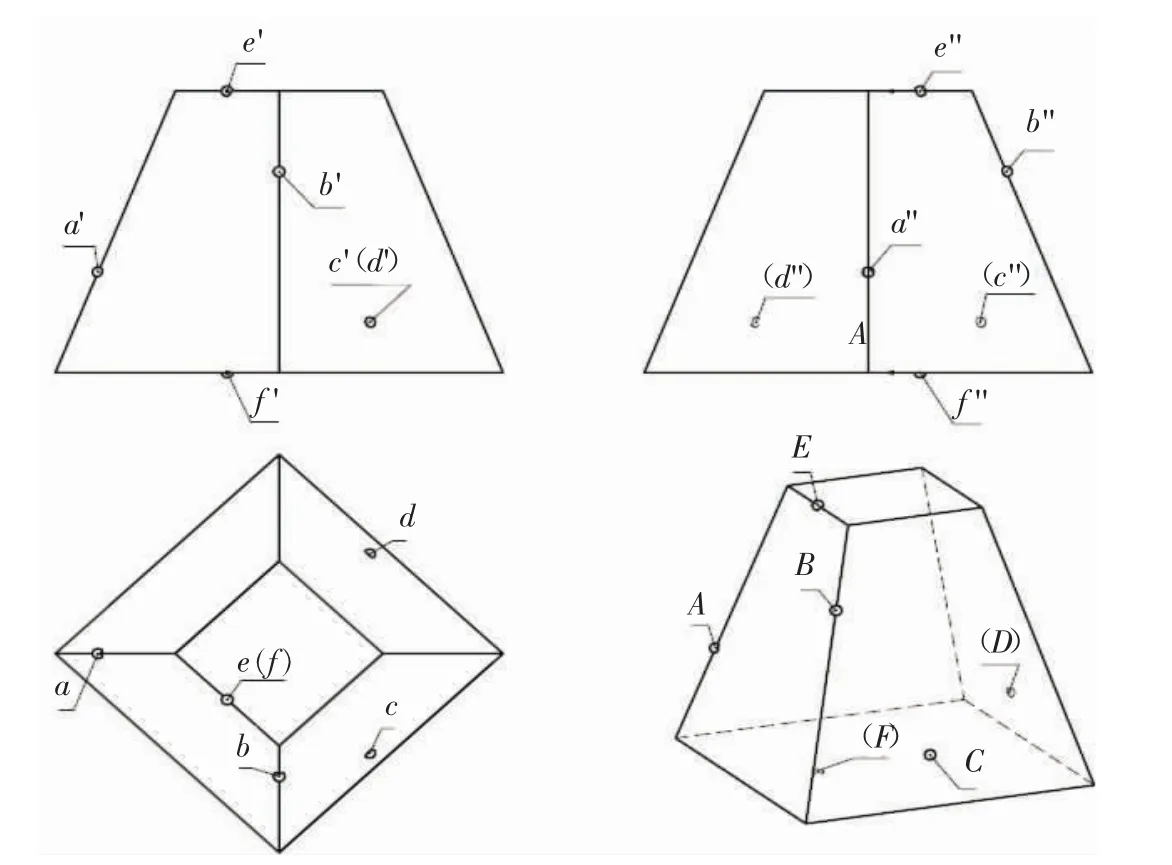
图5 四棱台及其表面上点的投影图和轴测图

这种方法制作的虚拟模型优点是表面上的点显示突出，易于观察，且形成的e-drawing 模型中点的显示也很清晰，可见性也随着模型的拖动和旋转而变化，图6 为对“点”标记注释后的模型上色图和线框图的效果；缺点是制作稍麻烦，且以小球实体表示点，与立体原型稍有不同，球与原立体也产生相贯线，对于初学者来说不易理解。

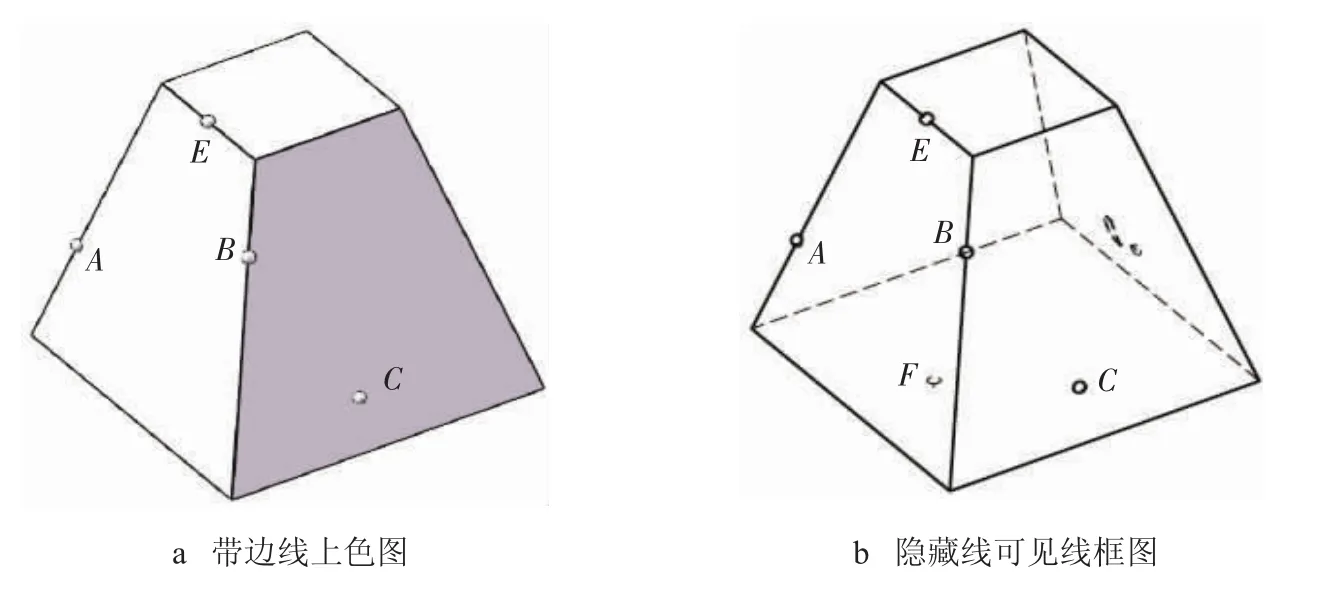
图6 四棱台及其表面上点的三维模型

2 创建曲面立体及其表面上点的虚拟模型

曲面立体是表面由曲面或者曲面和平面所构成的实体，主要包括圆柱、圆锥、球和圆环等。以图7 所示“补画圆台表面上各点的二面投影”［7］为例，介绍第3 种立体表面上点虚拟模型的制作方法。

图7 圆台及其表面上的点

（1）按照尺寸创建圆台模型；

（2）在“上视基准面”绘制草图，草图为大小与立体成比例的一个圆（通常可取直径为1～1.5 mm），并通过“几何关系”和尺寸，使圆与表面上点的位置一致；利用“曲线＞分割线”功能，将草图向圆台上、下面投影，分别在相应的面上分割出圆形的面域，用该面域表示面上的点；

（3）按此方法，将立体上每个点所在位置的表面均分割出小的“面域”；

（4）新建工程图文档，插入表面用面域表示点的圆台的3 个视图和轴测图，并对每个点添加注释（点不可见加括号），如图8 所示。

图8 圆台及其表面上点的投影图和轴测图

用一个小面域表示一个点，以便增强“点”的辨识性，可在轴测图和e-drawing 模型中将点清晰地显示出来，是这种方法与前两种制作虚拟模型的区别。优缺点与用小球表示点相同，但制作更方便一些。在上色模型中，可将表示点的面域设置为另外一种颜色，使点的显示更为突出，图9 为该模型上色图的效果。

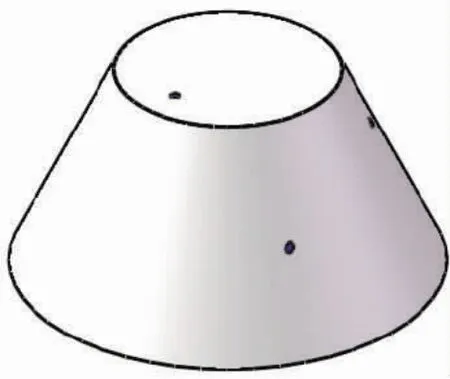
图9 圆台及其表面上点的三维模型

3 创建立体及其表面上线的虚拟模型

3.1 平面立体表面上线的虚拟模型制作

以图10 所示“正五棱柱及表面上折线ABCDE”［8］为例，说明“平面立体表面上线”虚拟模型的制作方法和注意事项。

图10 棱柱及其表面上的线

（1）按照尺寸创建正五棱柱模型；

（2）分别在各段折线所在的棱柱表面上绘制草图，并通过添加“几何关系”和尺寸，使草图中的直线与表面上各折线的位置一致；

（3）由于线段AB 未将其所在表面完整分割，故其草图画成一个宽度很窄的矩形，如图11 所示（图中为了显示该矩形，宽度比较大，实际制作模型时，矩形宽度可设置为0.01 mm 或更小）；

图11 线段AB 的草图

（4）利用“曲线＞分割线”功能，将草图分别向每段直线所在的棱柱表面投影，则相应的棱柱表面被分割为两个面域，表面上的线就是面域的分界线；

（5）新建工程图文档，插入五棱柱的3 个视图和轴测图，并对直线端点添加注释（点不可见加括号），如图12 所示。在图中的水平投影、正面投影和轴测图中，隐藏了表示线段AB 矩形的多余三条边线；若矩形的宽度比较小，则不影响显示效果，也可不隐藏；

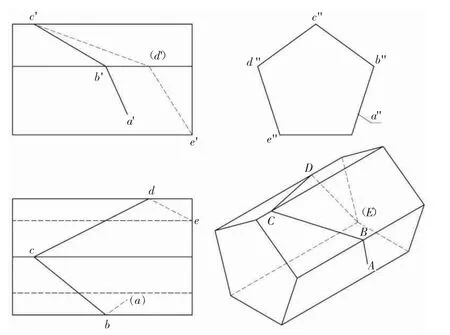
图12 五棱柱及其表面上线的投影图和轴测图

（6）在棱柱表面标注出线的各端点，并保存为e-drawing 格式的模型。在模型中，旋转立体以不同视角观察可见，棱线和表面上线的可见性，是随着观察视角的不同而变化的，如图13 所示。

图13 五棱柱及其表面上线的三维模型

3.2 曲面立体表面上线的虚拟模型制作

常见曲面立体表面上线的题型，线一般没有将曲面完全分割为两部分，制作虚拟模型时需要用封闭草图分割曲面。以图14 所示“圆柱及其表面上的线”［8］为例，说明圆柱面上一般曲线虚拟模型的制作方法。

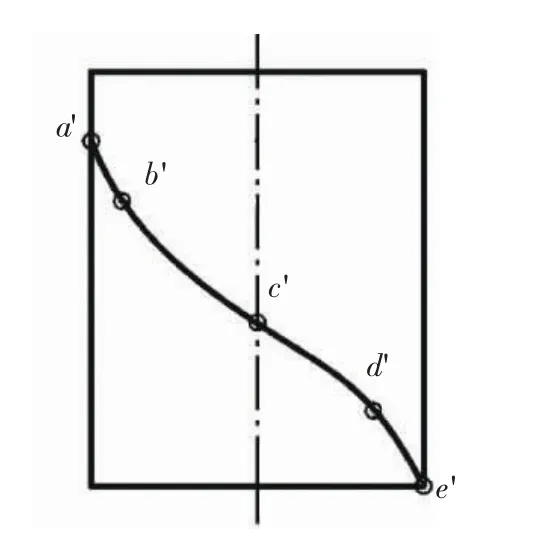
图14 圆柱及其表面上的线

（1）按照尺寸创建圆柱模型；

（2）确定曲线上A、C、E 三个特殊位置点，并找出若干个一般位置点（如图中B、D 点）；在“前视基准面”上新建草图。首先画出这些点，并通过添加“几何关系”和尺寸确定点的位置，然后作通过各点的样条曲线；最后通过“等距实体”、绘制直线、“修剪”等操作，使草图形成如图15 所示的封闭线框（图中为了显示该线框，宽度比较大，实际制作模型时，宽度可设置为0.01 mm 或更小）；

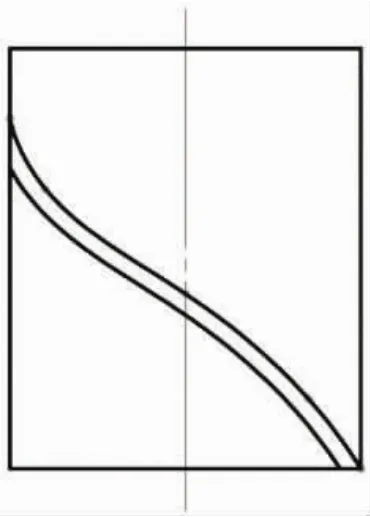
图15 圆柱及其表面上的线

（3）利用“曲线＞分割线”功能，将草图向前半圆柱面投影，则圆柱表面被分割出一个面域；

（4）新建工程图文档，插入圆柱的3 个视图和轴测图，并对曲线上的特殊点和一般点添加注释（点不可见加括号），如图16 所示。在图中的正面投影、侧面投影和轴测图中，隐藏了“等距实体”作出的样条曲线；若草图中线框的宽度比较小，则不影响显示效果，也可不隐藏；

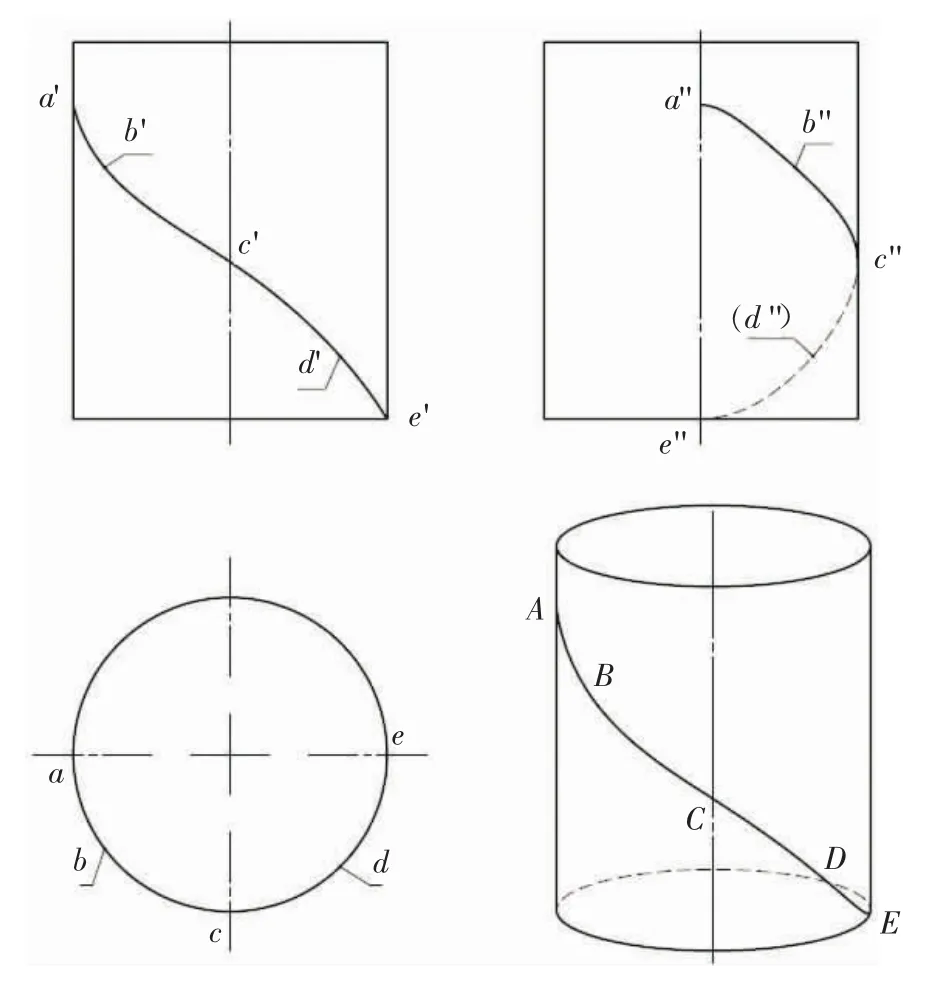
图16 圆柱及其表面上线的投影图和轴测图

（5）通过保存为e-drawing 格式文件，可创建该立体的虚拟模型。

4 结语

在“工程制图”课程的教学中，利用SolidWorks 建立种类齐全、数量丰富的虚拟模型库，可弥补传统教学工具和手段的不足。借助虚拟模型的三维动态演示和轴测图的直观性，可将课程中的重点、难点内容清晰、形象地展示出来，帮助学生提高空间想象和思维能力，为后续进一步学习立体的截交线、相贯线和组合体奠定坚实的基础。随着“新工科”和“混合式教学”等改革实践的深入开展，应不断地创新方法来补充、完善虚拟模型库，更好地培养学生的空间想象思维能力、观察能力、自主学习能力、创新能力和工程意识。