高负荷低压涡轮时序效应数值模拟与试验验证
2023-11-27杨晓军宋立旗宁嘉昕康晋辉
杨晓军,宋立旗,宁嘉昕,康晋辉
(中国民航大学航空工程学院,天津 300300)
0 引言
低压涡轮是航空发动机中质量占比最大的部件[1-2],对航空发动机减重的关键在于减小低压涡轮的重量。其中,利用叶轮机械内部固有的非定常性来提高涡轮性能是国内外研究热点,具体的思路分为2种:一是采用高负荷的叶型设计,其难点在于如何控制吸力面附面层的分离损失,国内外学者针对此难点已做了大量研究[3-5];二是减小叶片排之间的距离,减小轮毂和机匣的重量,这使得下游势流的影响更加突出,加剧了叶片排之间的非定常效应。
叶片排之间的非定常效应与很多因素有关,如叶片排之间的间距、动静叶的数目比、叶片周向的相对位置等[6]。季路成等[7]的研究表明,动静叶干涉主要受到时序效应的影响;Adolfo 等[8]对叶片排不同相对周向位置的分布进行了研究,指出涡轮效率一般呈正弦形式波动;Zhao 等[9]研究了时序效应对于叶片载荷的影响,并指出在时序效应的影响下叶片载荷存在1个最小值。同时,国内外针对吸力面附面层流动特性与分离转捩机理做了大量研究。Zhang等[10]研究了不同雷诺数与湍流度条件下尾迹与低压涡轮附面层的相互作用,并指出在低雷诺数、低湍条件下,尾迹与分离附面层相互作用造成的损失主要由K-H不稳定性诱导的卷起涡引起;罗华玲等[11]研究了尾迹在叶栅通道内的输运,细化了边界层流动机理;Jacobs 等[12]的研究表明,叶片前缘边界层存在剪切遮蔽效应,并因此会在下游位置形成Klebanoff 条纹;Coull 等[13]指出尾迹放大Klebanoff 条纹前缘、最强条纹和尾缘分别以主流速度的88%、70%、50%向下游传播。
现有的研究成果主要是针对于时序效应对低压涡轮的时均效率等性能参数的影响,而针对于边界层分离转捩特性的研究也仅仅考虑了上游尾迹的影响,并未对上游尾迹耦合下游势流做深入研究,因此对于时序效应的内部流动机理的理解不够透彻。为真实的模拟发动机的非定常性,本文采用下游势流耦合上游尾迹的双重扰动的方法,选取0°和180°2 个相位工况,通过边界层分离和转捩分析、积分参数以及瞬态分析3方面,对比0°和180°2个相位的边界层形态,对时序效应的内部流动机理开展研究。
1 数值模拟与试验验证
1.1 数值模拟
本文的工况设置为出口雷诺数Re=1.6×105(以轴向弦长为特征尺度),湍流度Tu=1.5%,流量系数Ф=0.83。
本文在UG 中建模,网格划分软件为ICEM,使用ANSYS-CFD 20.0商用求解器进行求解。数值方法为RANS收敛后接LES进行计算。由于LES存在滤波功能,所以选取何种亚格子模型是LES精度的关键。本文采用Smagorinsky 亚格子模型,空间离散项采用中心差分,时间离散项采用2 阶精度的向后欧拉积分。引入Van-Driest 壁面函数来修正Smagorinsky亚格子模型造成的近壁面涡粘度过大的问题。网格拓扑结构如图1所示。
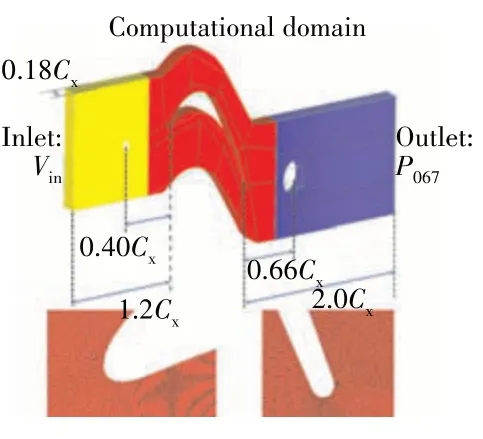
图1 网格拓扑结构
叶片尾缘距出口平面为2.0Cx(Cx为叶栅的轴向弦长),可以保证在叶栅通道的下游充分掺混,下游圆棒距叶片尾缘为0.66Cx,上游圆棒距叶片前缘为0.40Cx,进口平面距叶片前缘为1.2Cx。据罗华玲[14]的研究,流体域的展向高度设置为0.18Cx,以保证涡结构能够在展向充分发展。上游圆棒主要用于产生尾迹,Pfeil 等[15]的研究表明,圆柱绕流产生的远场尾迹与叶栅的远场尾迹有几乎相同的湍流特征,确定圆棒的直径关键在于确定其气动损失。根据Mahallati[16]的研究,圆棒的气动损失系数为
式中:CD为圆棒表面的摩擦系数,本文取1.05;Sb为栅距;Z为叶片的Zweifel 载荷系数,T106A 的载荷系数为1.04。
根据本文的气动参数以及总压损失系数的范围,可得上游圆棒直径为2.05 mm。下游圆棒的直径为47.5 mm,据Maciej 等[17]的研究表明,当下游圆棒的直径为47.5 mm 时,其对吸力面造成的压力扰动与真实叶片的势场造成压力扰动相当。转静交界面设置为冻结转子(Frozen Rotor)模式。
为了较为准确的捕捉叶片表面的分离、转捩流动状态,在叶片近壁面一周做“O”型拓扑,其余的区域做“H”型拓扑。为保证y+<1,叶片壁面法向上第1 层网格最大高度为0.003 mm,叶片整体网格质量在0.55以上。
计算域整体网格数量为1800 万,其中叶片的网格数量为1500 万,下游圆棒的网格数量为128 万,上游圆棒的网格数量为172万。叶片近壁面1周网格节点数为945,流向节点为800,周向节点数为325,展向节点数为60。非定常单步时间步长为0.00001253 s,将1 个尾迹扫掠周期拆分为500 步。先用RANS 计算定常流场,计算模型为SST 耦合γ-θ转捩模型。以RANS 收敛结果作为LES 的初场,共计算7 个尾迹扫掠周期。为保证计算的准确性,本文仅对LES计算结果的后6 个周期进行处理,并每隔2 个周期进行锁相平均。待LES出现较好的周期性做瞬态分析,计算采用1 台16 核32 线程工作站,完成整个工况计算共耗时2个月。
1.2 试验验证
本文的试验验证依托中国民航大学平面叶栅试验台,如图2 所示。试验台主要由上游尾迹模拟机构、下游势场模拟机构、叶栅通道、测试系统组成。为获得叶片壁面静压数据,在测试叶片的吸力面布置了31 个静压孔,并在吸力面的逆压梯度区对静压孔进行加密,压力面布置了5个静压孔。静压孔布置在45%叶高处。

图2 平面叶栅试验台
T106A的叶型参数及工况参数见表1。

表1 T106A叶型参数及工况参数
流量系数Ф为
式中:Ux为叶栅进口轴向速度;Ub为上游圆棒线速度。折合频率Fr为
式中:Cx为叶栅的轴向弦长。
为验证数值模拟的准确性,采用载荷系数进行对比验证,其中载荷系数为
式中:下标in 表示进口参数,out 表示出口参数,local表示测试处参数,0 表示总压,以出口动压进行无量纲处理。
在t/T=0 时,上下游圆棒相对位置如图3 所示。图中虚线箭头表示上游圆棒的运动方向,实线箭头表示下游圆棒的运动方向。当下游圆棒在环向的位置与叶片尾缘平齐时,此时上游圆棒和下游圆棒的相对相位角定义为0°;当下游圆棒位于叶栅通道中间位置时,将此时的相位角定义为180°。
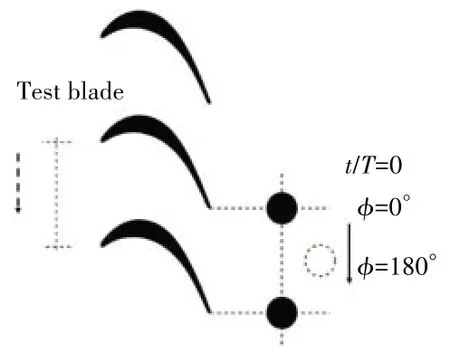
图3 t/T=0时,上下游圆棒相对位置
0°与180°相位时均载荷分布如图4 所示,其中散点是试验采集的结果,实线是数值模拟的结果。由于本文主要侧重于吸力面的附面层特性,故只给出了吸力面的载荷分布。横坐标是流向坐标,以吸力面长度(Suction Surface Length,SSL[10])做无量纲s,并在之后的分析过程中,将每一点笛卡尔坐标系下的数据转换为以流向-壁面法向为正交坐标系下的数据,将几何复杂的实际流动转换为流向和壁面法向的流动。在峰值点上游,2 个相位试验结果均与数值模拟结果吻合程度较好,峰值点之后数值结果与试验结果基本吻合。从图中可见,在峰值点之后,试验和数值结果均观测不到明显的压力平台。对比2 个相位的结果可知,2 个相位的峰值点位置基本一致(0.44S0),180°相位的时均载荷峰值比0°相位略低。在峰值点之后180°相位的载荷分布曲线比0°相位更平滑。
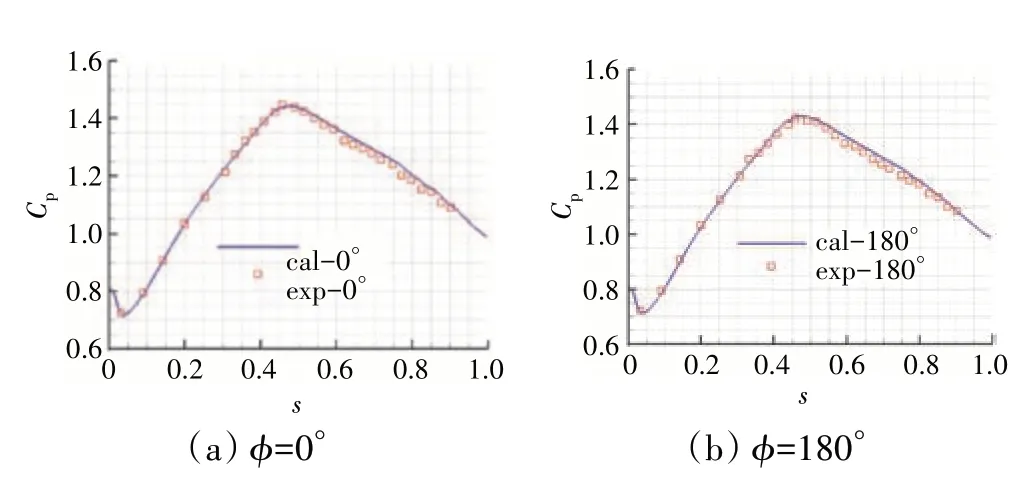
图4 0°与180°相位时均载荷分布
2 结果与分析
2.1 边界层分离与转捩分析
不同相位边界层边缘速度(s=0.95)如图5 所示,叶栅出口速度为无量纲。线A、B、E分别代表0°相位时的尾迹前缘、尾迹中心以及尾迹尾缘。其中,尾迹前缘具有最大的正向扰动速度,而尾迹尾缘具有最大的负向扰动速度(即尾迹的负射流效应)。从图中可见,在尾迹通过的时间内,边界层边缘速度波动幅度明显。在不同的相位角耦合的情况下,速度波动范围有所不同,0°的波动范围最大,180°的波动范围最小,且不同相位下速度峰值与谷值的时间并不相同。

图5 不同相位边界层边缘速度(s=0.95)
不同相位的时均总压损失系数如图6 所示。总压损失系数为
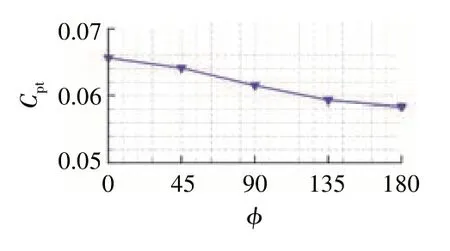
图6 不同相位的时均总压损失系数
式中:下标的含义与载荷系数的定义一致。
从图中可见,0°相位的总压损失最大,而180°相位的总压损失最小,且随着上下游圆棒相对相位角的增大,时均总压损失逐渐减小。结合图5和图6,0°相位的边界层边缘速度波动速度最大且总压损失最大,而180°的速度波动最小且总压损失最小,故在下文着重分析以上2个相位的流动情况。
2 个相位吸力面时均壁面剪力以及均方根RMS分布情况如图7所示。

图7 吸力面时均壁面剪力以及均方根
由于分离和转捩位置具有很强的非定常性,所以本文讨论的分离和转捩位置均是时均的位置。从图中可见,2 个相位角的壁面剪力的趋势基本一致,从吸力面峰值点往后,壁面剪力均一直下降,且下降的速度逐渐加快,这是因为在逆压梯度的作用下,壁面附近的速度下降的趋势增强。对于0°相位,在0.68S0处下降到1 个很低的水平,说明此时吸力面发生了分离,在之后的0.72S0位置壁面剪力逐渐上升,对应于分离泡中的回流区域。相对应的180°相位,其分离位置相较于0°相位向上游移动(0.65S0),且其回流区域对应的位置为0.74S0。
为了更准确的描述转捩过程,引入壁面剪力的均方根值
式中:xavg为算数平均值。
QRMS值越大,说明壁面剪力关于平均剪力的波动越大,当转捩开始时,速度开始剧烈波动,因此,可以通过QRMS的变化情况判断转捩位置。对于0°相位,壁面剪力的QRMS值在0.70S0处突然增加,说明流动速度波动增加,转捩开始;而180°的QRMS值突然增加的点则在更上游的位置即0.68S0。这意味着180°相位时分离和转捩起始位置均向上游移动。随着转捩的进行,2 个相位的壁面剪力的QRMS一直上升。0°相位在0.84S0处RMS值达到极大值,之后减小至0.93S0处出现1 个谷值,这表明分离剪切层再附。而对于180°相位,其在0.92S0处达到极大值,在0.95S0处出现谷值,即180°相位时在0.95S0处剪切层完成了再附。
边界层形状因子H12及动量厚度θ如图8所示。

图8 边界层形状因子H12及动量厚度θ
从图中可见,在0°相位,动量厚度在0.77S0处有1 个拐点,动量厚度迅速增大,并随着转捩进程的迅速进行,边界层的动量损失急剧增大。此外,形状因子出现了峰值点,且峰值点的位置与动量厚度转折点的位置重合。这是因为在转捩加速时,分离剪切层与主流之间存在剧烈的掺混,使得边界层动量损失急剧增大;掺混的同时会带来能量交换,剪切层内的流体能量增加,边界层的速度型逐渐趋于饱满。在180°时,动量厚度的拐点和形状因子的峰值点均向上游移动(0.71S0),在吸力面尾缘,180°相位的动量厚度比0°相位要低,其具体原因在后文解释。
2.2 边界层积分参数
0°和180°相位吸力面载荷系数时空如图9 所示,图中虚线表示下游势流单独作用时边界层边缘最大和最小速度(以出口速度做无量纲),线A、B、E分别代表尾迹前缘、尾迹中心以及尾迹尾缘。图中还叠加了2 条水平线用于表示下游势流的压力扰动,下游势流造成的压力扰动以声速传播,因此下游势流造成的压力扰动瞬间即可完成。下游势流对于上游的影响主要是拥堵效应。在t/T=0 时,圆棒中心距离叶片尾缘最近,下游圆棒对于吸力面尾缘的拥堵效果最明显,因此之后吸力面尾缘的边界层开始剧烈减速。

图9 0°和180°相位吸力面载荷系数时空
从图中可见,载荷系数的值在0.44S0~0.70S0处强烈波动。沿着尾迹中心B的路径,有2 个衍生结构(C和D),这2 个结构与尾迹诱导转捩产生的卷起涡有关。Stieger 的研究表明[18],尾迹的负射流效应会导致吸力面压力周期性波动。从图中可见,在1 个尾迹扫掠周期内,除了尾迹负射流造成的压力波动外,载荷系数在0.8T、1.8T、2.8T再次达到峰值,此时的峰值是由于小于势流的扰动造成的。最大正向扰动速度线(线A)与最大速度线相交,此时压力波动与速度扰动具有相同的相位。
与0°相位相比,180°相位时表面压力的波动在时间上的长度减小,此时,最大正向扰动速度(线A)与最小速度线相交,压力波动和速度扰动异相。在180°相位时,没有观察到与衍生结构相关的压力波动,这说明此时由分离泡脱离的卷起涡的尺度较小。
0°和180°相位吸力面形状因子时空如图10 所示。图中的线A、B、E与图9 中的一致,线F、G分别表示寂静区的前缘和尾缘。沿着尾迹中心的路径(B),形状因子增加,这是由边界层的黏性效应导致的,尾迹带来的加速效果使得边界层面外部被加速,而靠近壁面的边界层加速具有时间上的迟滞,速度型被扭曲。在尾迹尾缘通过后,由于尾迹的高湍特性,会触发转捩机制,形成湍斑,湍斑前缘和尾缘向下游传播的速度不同,在时空图上形成1 个楔形的湍流条带。紧随湍斑的是寂静区,该区域内边界层具有饱满的速度型,且其呈现出层流的流动特征,抗分离能力较强,具有低耗散的特征,因此寂静区的强弱决定了叶型损失的大小[11-13]。

图10 0°和180°相位吸力面形状因子时空
0°和180°相位吸力面动量厚度时空如图11 所示。图中各标识与图10一致。从图中可见,2个相位动量厚度增加均集中于吸力面尾缘。对于0°相位,动量厚度增加主要分为2 个区域,第1 个区域位于尾迹中心和尾迹尾缘(线B和E)之间,此时动量厚度增加与尾迹与边界层相互作用有关。在尾迹向下游传播的过程中,尾迹的高湍特性会触发转捩机制,诱导边界层发生转捩并产生湍流条带。第2 个区域位于尾迹尾缘和湍流条带尾缘(线E和F)之间,此时动量厚度的增加与下游势流有关。势流在向上游传播的过程中,其造成的压力扰动会使得转捩起始点向上游移动,湍流浸湿面积增大,吸力面尾缘边界层的动量损失增加。180°相位吸力面尾缘动量厚度增大的区域明显减小,且主要集中于尾迹尾缘(E)和湍流条带尾缘(F)之间。

图11 0°相位与180°相位吸力面动量厚度时空
在0°相位时,寂静区处于下游势流周期内的加速阶段,逆压梯度的强度逐渐增加,寂静区保持层流的能力被此强烈的逆压梯度削弱。而在180°相位时,寂静区处于下游势流周期内的减速阶段,逆压梯度的强度逐渐减小,寂静区的持续时间以及流向尺寸均有所增加,尽管此时分离和转捩起始位置向上游移动,致使湍流湿面积增加,但是其带来的湍流损失被更饱满、抗分离能力更强的寂静区所平衡,故180°时吸力面尾缘的动量损失相较于0°而言要小。
K-H卷起涡的发展如图12 所示,图中横坐标为无量纲流向坐标s=0.65~0.80,纵坐标为无量纲壁面法向距离(以叶栅栅距为无量纲),其中黑色线表示卷起涡的轨迹。尾迹在向下游输运的过程中,其大尺度扰动会导致分离剪切层的卷起,这一过程由无粘的K-H不稳定机制所主导的,其主要特征是大尺度涡的卷起、脱落和配对等,同时伴随着能量交换和耗散[18]。从图中可见,0°相位卷起涡的涡量较大,且卷起涡形成、脱落及破碎过程发展迅速,而180°卷起涡的涡量较小,其发展速度也较慢,这与图9 的结论一致。从卷起涡发展的空间分布上看,180°相位卷起涡的分布更靠近上游。

图12 吸力面尾缘动量厚度的变化
吸力面尾缘动量厚度的变化如图13 所示。在定常情况下,0°相位的动量厚度比180°时的动量损失大。2个相位的动量厚度在1个尾迹扫掠周期内波动明显,180°相位的动量厚度整体低于0°相位,且其波动范围比0°相位小。结合上述的时空云图,动量厚度最大的时刻出现在尾迹中心通过之后,而最小值出现在寂静区所持续的时间内。180°动量厚度峰值点出现的时刻相较于0°延迟了0.1T,但是动量厚度较小值维持的时间比0°相位的持续时间长,且在寂静区通过的时间内,动量厚度维持在一个较低的水平,即寂静区的抑制分离的能力较强。

图13 0°和180°相位2个工况在1个尾迹扫掠周期内的瞬态流动
2.3 瞬态流动分析
0°和180°相位2个工况在1个尾迹扫掠周期内的瞬态流动情况如图14 所示。图中叶栅通道内用流向涡量Wx表示尾迹的输运情况,采用半边界层高度处的壁面法向涡量Wy表示Klebanoff 条纹,使用Q参数来识别叶片尾缘的涡结构,并用流向速度Vx进行着色,其中Q=2.2×105。
从图14(a)、(b)中可见,在0.04T时,尾迹中心运动至通道中心,而尾迹尾缘刚接触叶片前缘。尾迹在叶栅通道内会发生弯曲和变形,故尾迹尾缘先接触叶片,而尾迹前缘在通道内流动尚未接触到吸力面,因此尾迹尾缘中的高湍扰动经过叶片前缘边界层的剪切遮蔽感受性过程后[19],产生被尾迹放大的Klebanoff条纹。因条纹前缘和尾缘的传播速度分别为0.88U和0.53U(U为主流速度)。由以上两个原因导致条纹的传播在时间上要滞后于尾迹的传播,且在向下游流动过程中条纹会不断拉伸。0°相位的条纹在展向上的分布较密集,且条纹强度相较于180°较强。在0.5S0附近壁面法向涡量均有所上升,这是由于尾迹前缘的抬升作用导致的。
从图14(c)、(d)中可见,在0.12T时,尾迹尾缘被叶片前缘切割,被尾迹放大的Klebanoff 条纹不断产生。此时尾迹中心到达分离泡所在区域,尾迹与分离剪切层相互作用并触发K-H不稳定性,形成大尺度的展向涡。从图14(a)、(b)的尾迹涡量以及上述的边界层速度波动可知,0°相位的尾迹携带的涡量较大,对边界层造成的扰动较大,因此其诱导并放大的Klebanoff 条纹强度更大。Wissink 等[20]的研究表明,全展向涡的卷起与尾迹流过分离泡时造成的大尺度速度扰动有关。0°相位尾迹对边界层造成的速度扰动较大,因此产生全展向的K-H涡,而180°时产生部分展向涡,且展向涡的尺度和强度均较小。对比吸力面载荷系数时空云图也可见2 个相位展向涡的区别。结合图10 和图12 可知,尽管180°相位K-H卷起涡在空间上的分布更靠近上游,但其尺度、涡量和强度较小,且由于0°相位卷起涡的发展迅速,在之后的破碎过程中能量交换和耗散要比180°相位剧烈得多。
从图14(e)、(f)中可见,在0.40T时,尾迹尾部流至叶片尾缘,0°相位被尾迹放大的Klebanoff条纹已运动至分离泡所在区域,而180°相位的条纹还未到达该区域。Klebanoff 条纹使得分离剪切层扭曲并抑制全展向涡的生成。当Klebanoff 条纹到达分离区域时,破坏了K-H结构并迅速破裂为小尺度的涡,加速了转捩的进程。
从图14(g)、(h)中可见,在0.50T时,尾迹中心作用于叶片尾缘,2 个相位条纹尾缘在0.20S0,0°的条纹前缘达到0.80S0处,180°的条纹前缘在0.72S0,表明0°相位时Klebanoff条纹覆盖的区域较大。
从图14(i)、(j)中可见,在0.80T时,尾迹尾部已经流出叶栅通道,下一条尾迹已进入叶栅通道,但由于此时尾迹尾部尚未接触到叶片前缘,前缘并无Klebanoff 条纹产生。在0.90S0下游均是小尺度的湍流结构,而在0.70S0与0.80S0之间没有明显的涡结构产生,这是由于尾迹通过之后的寂静区导致的。
3 结论
(1)不同相位的差异是由于势流造成的压力扰动与速度扰动的相位,这将影响尾迹诱导转捩带来的湍流损失与寂静区之间相互作用。0°相位时,下游势流压力扰动与速度扰动是同相的,寂静区处于逆压梯度逐渐加强的阶段,寂静区的抗分离能力被削弱;而180°时,势流的压力扰动与速度扰动异相,寂静区的保持层流的能力较强,使动量损失减小。
(2)0°相位尾迹的涡量较大,对边界层边缘速度的扰动较大,大尺度扰动在尾迹经过之后使得分离剪切层弯曲并发生卷起,产生大尺度的全展向涡,意味着剪切层与主流之间存在较强的能量掺混,且之后全展向涡破碎成小尺度的湍斑时,会带来更大的能量耗散,因此0°相位在尾缘造成较大的动量损失。同时这种大尺度扰动在尾迹尾部接触到叶片前缘时,会产生强Klebanoff 条纹并在之后的流动过程中放大,条纹的强度比180°相位的大,条纹在到达分离区域时使K-H结构迅速破碎,加速了转捩进程,因此0°相位的再附点要比180°更靠近上游。
