固液相平衡计算研究进展

2023-11-25项曙光赵芳磊孙晓岩赵文英陈玉石

青岛科技大学学报（自然科学版） 2023年6期

项曙光,赵芳磊,孙晓岩,赵文英,陈玉石

((1.青岛科技大学过程系统工程研究所,山东青岛 266042;2.齐鲁师范学院化学与化工学院,山东济南 250200;3.石化盈科信息技术有限责任公司,上海 200120)

相平衡在化工中的地位非常重要,化工生产过程中,原料的预处理、物料的反应、产物与副产物的分离,均需基于相平衡进行分离。与应用相对广泛的汽液平衡和液液平衡相比,固液平衡同样重要。液液平衡常用于萃取过程,固液平衡常用于结晶过程,结晶过程的能耗一般低于精馏操作过程,结晶在工业生产中具有一定的优势。固液相平衡较汽液平衡和液液平衡系统更为复杂,固态溶解的有限溶解度、多晶型、共晶体等。固液平衡可分为两类,一类是溶解平衡,是不同化学物质的液体和固体间的平衡,讨论的重点是固体在液体中的溶解度问题;另一类是熔融平衡,是相同化学物质的熔融和固体形式间的平衡。

固液平衡与其他相平衡一样,符合相平衡的基本判据,固液两相的温度、压力相等,各组分在两相中的化学位和逸度相等。固液平衡的液相由状态方程或活度系数计算组分i在液相的逸度,固相由活度系数或状态方程计算组分i在固相的逸度,即式(1)、(2)、(3):

许多学者一直在对固液相平衡模型进行完善。1986年金克新等[1]对固液相平衡计算模型进行了概述,改进汽液相平衡模型用于低共熔物系的固液相平衡的计算。曲红梅等[2]对有机物系固液相平衡计算模型的研究进展进行了介绍,深入分析了用于固液平衡计算的UNIFAC 活度系数模型。陆小华等[3]对电解质溶液固液相平衡进行了长时间研究并开发出PHEES电解质溶液相平衡软件,用于电解质溶液的活度系数、渗透系数、表观相对摩尔焓、蒸汽压和溶解度等多种热力学性质的计算。黎文超等[4]和岳金彩等[5]在经验方程模型方面概述了固液相平衡的研究进展。URSZULA 等[6-9]对大量二元和三元非电解质物系固液相平衡进行了实验,并着重使用DISQUAC模型及修改的UNIFAC 模型对固液相平衡的性质进行预测,最后与实验数据进行对比。DynoChem 公司对大量非电解质物系的固液相平衡实验数据进行了汇总,可以提供结晶过程中溶剂和反溶剂的筛选,并能用UNIFAC模型自动生成模型预测的溶解度数据与实验溶解度数据的回归对比图。

本研究拟概括和分析固液相平衡计算的活度系数模型、经验模型和状态方程模型。文章对液相活度系数模型及基于局部组成理论和基于正规溶液理论的固相活度系数模型分别进行概述,分析适用不同体系的模型的优缺点,模型的修正及发展历程。研究固液相平衡、活度系数模型、经验模型和状态方程模型,对于固液相平衡模型的理论研究、模型改进、应用具有重要的意义和实用价值。

1 固液相平衡方程式

在固液平衡计算时,液相逸度在常压下(0.1 MPa)通常采用液相活度系数模型计算,在高压下(0.1～200 MPa)通常采用状态方程模型计算。固相逸度通常采用固相活度系数模型计算,固相活度系数的处理一般有3种情况:(1)固相为理想溶液,即γi,S=1。(2)对于简单共晶体系,固体将以纯组分的形式结晶,固相不互溶,x i,Sγi,S=1。(3)熔融过程用固相活度系数法求解真实γi,S。

1.1 常压固液相平衡模型

固液相平衡的热力学模型主要应用于常压条件下(0.1 MPa),用液相活度系数表示固液相平衡中液相的非理想性,用固相活度系数表示固液相平衡中固相的非理想性,如式(1)。

纯物质组分i的逸度的定义为(T一定):

将(1)式方程两边移项取对数并将(4)式在等温等压下由纯固体状态积分到过冷纯液体状态联立方程可得:

方程联立得到了常压下固液平衡的方程式:

当温度比较接近熔点时,热容差的贡献往往可以忽略不计。当忽略这些项时,可以得到非常简单的关联式。除了活度系数,固液平衡求解溶解度x i,L需要熔化焓ΔH i,f和熔点温度T i,f,均可从手册中查得:

1.2 高压固液相平衡模型

当混合物中溶解有低相对分子质量的气体时,压力改变了液相溶液的非理想性,对固液平衡的影响较大。高压下(0.1～200 MPa)通常采用状态方程计算液相的非理想性,如式(2)。

对于固相,仍采用活度系数模型表示其非理想性,但要进行压力校正。若以常压P0为参考压力,则在参考压力P0下固相中组分的分逸度为

在体系温度压力下(高压),固相组分i的分逸度可由对偏摩尔体积积分得到:

由式(2)、(10)、(11)可得

常压和高压条件下的固液相平衡模型的计算时,液相活度系数和固相活度系数的计算是计算的关键。而对纯固体饱和体系的相平衡计算可通过经验模型计算纯固体在液相中的溶解度,进而计算固液平衡。下面将分别介绍活度系数模型、经验模型和状态方程模型的发展历程及模型特点。

2 活度系数法

2.1 Pitzer模型

1973年DEBYE 修正了D-H 理论[10],同时兼顾长程相互作用和短程相互作用,摒弃了之前的假设,并采用维利展开式描述吉布斯自由能,从而可以推导出其他的热力学表达式,得到了经典的半经验Pitzer模型。该模型考虑了短程“硬核效应”的位能、长程静电相互作用能和三离子间相互作用能三项,但适用的浓度较低。Pitzer模型是用于计算电解质水溶液体系(尤其是离子强度为6 mol以下的强电解质体系)的活度系数等热力学性质较为准确的电解质活度系数模型,也是目前应用最广泛的电解质活度系数模型。但Pitzer也有局限性,那就是计算过程中参数较多,适用范围有限。1975 年PITZER 等[11]针对电解质水溶液体系添加了静电非对称混合项;1980 年PITZER 等[12]用Margules方程修正了短程项,扩大了浓度的适用范围。之后研究者对Pitzer模型进行了修正和完善。FUERST和RENON 等[13]研究了多种参数对模型用于1-1型电解质固液平衡的影响;LI等[14]修正了Pitzer模型并推出了以氯化钠水溶液为实例可以适用于高温高压下的新的Pitzer-Li方程;同年SIMONSON等[15]针对电解质复杂多组分可互溶体系提出了Pitzer-Simonson方程;KIM 等[16-17]回归了25℃下高浓度混合电解质水溶液体系的参数;CLEGG等[18]在25℃对H+、Na+、K+、Cl-、NO3-为实例,扩展了Debye-Hueckel项,Margules方程扩展到了4个后缀项,得到了适用于对称混合电解质体系的Clegg-Pitzer模型,同年CLEGG 等[19]又把一个Debye-Hueckel项扩展到了包含电解质不对称体系的影响,Margules方程也是扩展到了4个后缀项,得到了可以适用于不对称混合电解质体系的Clegg-Pitzer模型;LI等[20-21]修正了Pitzer模型,用Clegg-Pitzer简化模型(Margules方程扩展到3个后缀项)对混合烷醇胺溶液中二氧化碳溶解度、甲基二乙醇胺与环丁砜水溶液中CO2和H2S溶解度的相关性进行预测,推导出Li-Mather模型,用于预测五元混合溶剂体系;PITZER 等[22]和CHEN 等[23]都对Pitzer模型进行了相应的修正和完善,PITZER 用CaCl2和MgCl2为实例,考虑了Pitzer方程高阶项对离子强度的依赖性的影响,修正了Pitzer方程,修改后的方程Pitzer有两个优点:一方面对于纯电解质,避免了计算离子浓度的缔合和相应的离子强度;另一方面对于混合电解质,避免了因为存在复杂添加项而导致的冗余。

KELLER 等[24]用1975年扩展的Pitzer模型测定了三价硝酸铁九水合物单一电解质水溶液在乙醇或1-丙醇溶剂中的溶解度,平均相对误差小于5%。CHEN 等[25]也用1975 年扩展的Pitzer模型计算NaCl、NaBO2、Na2B4O7混合电解质在水中的溶解度,平均相对误差小于3%。GALVAO 等[26]用Pitzer模型对NaCl、KCl、NH4Cl在乙醇和水为混合溶剂中的溶解度数据进行关联,平均相对误差仅为1%。由此可见,Pitzer模型可以很好描述电解质体系的固液相平衡。

2.2 ELECNRTL模型

CHEN 等[27]基于同种离子间相互排斥和局部电中性这两种假设的基础上描述了单一电解质水溶液体系的热力学性质,后来MOCK 等[28]将其扩展到了混合溶剂的电解质体系。该模型可以计算的电解质体系的超额吉布斯自由能主要包括两种贡献,贡献之一是中心离子物种附近邻域的离子与离子之间的长程静电相互作用;贡献之二是任何中心粒子附近邻域的所有离子间的短程静电相互作用。扩展的非对称Pitzer-Debye-Hückel(PDH)方程[12]被用于表示长程静电相互作用,基于局部组成[29]理念发展起来的NRTL(非随机两液相)理论被用来表示短程静电相互作用。所以ELECNRTL模型的超额吉布斯自由能为这两个贡献的加和。

此模型的特定优点如下:

1)CHEN 等[27]将ELECNRTL 模型很好的关联了许多不同类型的单一强电解质水溶液。

2)ELECNRTL模型与Pitzer模型的计算结果相比,精度稍差一些。但相关结果表明,若仅使用二元交互作用参数而不使用高阶参数,该模型可获得令人满意的精度,并且对浓度具有广泛的适用性。

3)CHEN 等[27]用ELECNRTL 模型对纯熔盐体系进行了关联,证明了该模型可适用于从纯溶剂到纯电解质的整个浓度范围。

4)当描述无限稀释电解质溶液体系时,该模型可简化为Debye-Hückel(DH 模型);当描述纯分子溶液体系时,该模型简化为NRTL模型。

CHEN 等[30]使用两贡献项的ELECNRTL 模型分别计算了NaCl、Na2SO4、FeCl2水溶液体系的液相活度系数,预测了这3种电解质在水中的溶解度,该模型可以很好的描述某些单一电解质水溶液体系的固液相平衡(SLE)。KIM 等[31]使用ELECNRTL模型计算门冬氨酸-鸟氨酸+水+甲醇混合溶剂电解质体系的固液相平衡(SLE),通过离子平均活度系数计算鸟氨酸在含水和甲醇混合溶剂中的溶解度,模型与实验数据吻合良好。YAN 等[32]、BHATTACHARIA 等[33-34]采用ELECNRTL 两贡献项模型准确描述了Na+-K+-Cl--SO24-混合电解质水溶液体系的多种热力学性质,结果表明,即使在饱和状态浓度和高温下,也能获得满意的结果。

2.3 Wilson模型

1964年WILSON 等提出了局部组成模型[35],对含烃、醇、醚、酮、腈、酯及含水、硫、卤素的互溶体系均能获得较好的结果。对二元溶液它是一个两参数方程,故只要有一组数据即可推算。并且计算精度较Margules方程和Van Laar方程高;仅由二元体系数据就可以预测多元体系的行为,而无需多元参数;但该方程不能用于部分互溶体系,不能用于活度系数有最大值的溶液。

COUTINHO 等[36-40]基于局部组成理论开发了适用于正构烷烃的固相活度系数模型,并对二元体系的实验数据进行了测试,可用于石油烃类体系固液相平衡的预测。COUTINHO 等[36-37]成功将局部组成模型(Wilson)的适用性扩展到了固相,原理就是用纯组分的升华热来估算局部组成模型的相互作用能量参数,并取得了良好的效果。LINDELOFF等[41]用COUTINHO 改进的Wilson模型计算正构烷烃混合物的高压固液相平衡,但该模型无法应用于有序固相与无序固相间的分离。

黎文超等[42]选用Wilson方程和方程拟合碳酸二苯酯在乙醇和碳酸二乙酯混合溶剂中的溶解度,Wilson方程的计算精度最高,平均相对偏差小于2%。邵先钊等[43]测定了内氯唑沙宗在7种有机溶剂中的溶解度,并采用4种模型对二元体系的溶解度数据进行了关联,结果表明Wilson方程的关联结果最好,平均相对偏差为0.69%。GHANAEI等[44]基于Wilson模型,通过纯组分在常压下的熔点温度和在高压下的熔点温度对Poynting进行修正,适合高压条件,该模型对不同压力下C14～C16熔点温度的预测效果比JI模型更接近于实验值,与实验值的平均相对误差小于0.36%。

2.4 NRTL模型

1968年PRAUSNITZ 等[29]提出了NRTL 模型,NRTL 方程是三参数方程,弥补了Wilson方程的不足,NRTL 方程可以应用于范围广泛含有水、醇、腈、胺、酯、酮、醛、卤代烃和烃的极性或非极性的混合物,可应用于汽液平衡和液液平衡,相较Wilson模型拥有更广泛的应用范围。沈志鹏等[45]测定了对甲基苯甲酸、间甲基苯甲酸、间苯二甲酸、邻甲基苯甲酸和邻苯二甲酸五种溶质在醋酸-水与醋酸-对应二甲苯混合溶剂中的固液相平衡数据,用NRTL模型能很好的关联该体系的固液相平衡数据,平均相对偏差为3.68%。CHEN 等[46-47]结合了Flory-Huggins方程和局部组成交互作用贡献思想提出了NRTL-SAC 模型,将液相中的非理想性转换为组分分子各片段的贡献总和。NRTL-SAC 模型将溶质和溶剂间的相互作用表示为3个片段(憎水性片段、极性片段和亲水性片段),并将分子间的相互作用转化为片段间的相互作用,这大大简化了液相活度系数的计算过程及溶剂筛选的过程,并且可以很好的预测溶质在混合溶剂中随混合分率变化的趋势。陆凤华等[48]使用NRTL-SAC模型来关联藜芦酸在纯溶剂和混合溶剂溶解度,平均相对偏差分别为4.24%和5.29%。

COUTINHO 等[39]开发了适用于固相的PNRTL局部组成改进模型,修正了组分参数的估算方法:用 MARANO 等[49]方法关联BROADHURST 数据[50]估算组分体积参数和表面积参数。对有序固相与无序固相间的分离进行了建模,克服了适用于固相 Wilson 方程[36-37]的局限性。PNRTL可以较为准确的预测固液相平衡中的组成和相态,结果比基于正规溶液理论获得固相活度系数的模型更加准确。

2.5 UNIQUAC模型

1975年ABRAMS等[51]提出了UNIQUAC 模型,他用局部体积分数作为主要的浓度变量,并推广Guggenheim 的似化学分析,从而进一步得到了液体混合物的超额吉布斯自由能的半理论方程。UNIQUAC是以双液膜和局部组成概念为基础的两参数活度系数方程,UNIQUAC 方程可以应用于范围广泛含有水、醇、腈、胺、酯、酮、醛、卤代烃和烃的极性或非极性的混合物,适用于分子相差较大体系的描述,该模型汽液平衡、液液平衡及汽液液平衡数据计算精确度可与NRTL 相比,但不再需要一个非随机因子。对于大多数非电解质混合物表示每两相汽液平衡和液液平衡只用两个参数;拟合参数通常表现出较小的温度依赖性,这使得它们更适用于外推。UNIQUAC 模型经过研究者的修正后[52-53],计算精度大大提高。GOMEZ等[54]用扩展的UNIQUAC 模型对硝酸钾在不同温度和盐酸浓度下的水-乙醇-盐酸混合溶剂中的溶解度进行了实验研究和建模,并将实验得到的硝酸钾溶解度数据用于扩展的UNIQUAC 模型相互作用参数的回归。

COUTINHO 等[39]开发了适用于固相的PUNIQUAC局部组成改进模型,修正了组分参数的估算方法。JI等[55]在模型中添加了熔点温度和压力之间的线性表达式,提出HWWAX-UNIQUAC模型用于固相活度系数的计算,改进正构烷烃的熔化焓、热容参数的计算公式,模型结果优于PUNIQUAC模型。GHANAEI等[56]基于基团贡献模型,提出了新的热容关联式,并对P-UNIQUAC模型进行改进,修改了交互作用能量参数,比较固相活度系数为1、UNIQUAC模型[51]、P-UNIQUAC[38-39]、修正P-UNIQUAC模型[56],对276～292 K 温度范围内二元、三元、多元混合物物系固体沉积量和固体析出温度预测结果平均相对偏差分别为14.54%、5.22%、4.43%、2.81%。GHANAEI等[57]通过引入Clapeyron方程将组分的热力学物性与相变发生时纯组分的摩尔体积变化联系起来,适合于高压条件,并将Pauly、Ghanaei、Nasrifar和新模型对高压下固体析出温度进行比较,对458组高压下数据预测结果的平均相对偏差分别为1.28%、1.39%、1.6%、1.27%,数据表明Ghanaei的新模型计算效果最好。SILVA 等[58]在交互作用能量中增加矫正参数Δλ并用HOOKE-JEEVES的方法进行参数估算,改进了P-UNIQUAC 模型,对固相溶解度的平均绝对偏差为0.342 5～0.776 7,优于原始的PUNIQUAC模型,模型结果与实验数据更加吻合。PEREIRA 等[59]分别采用P-UNIQUAC 模型和UNIFAC模型描述食用脂肪的固相和液相非理想性,并关注模型预测的混合物中TAG(三酰甘油)的组成,数据表明,模型对脂肪的固体含量和TAG(三酰甘油)组成的预测值与实验值较为吻合,平均绝对偏差为16.90%。

2.6 正规溶液理论模型

WON 等[60-61]基于正规溶液理论,假设所有组分都是可结晶的,用纯组分的升华热估算固相溶解度参数,并使用溶解度参数分别表示液相和固相的活度系数。SCHOU 等[62]修正了WON 模型中的熔点温度关联式,PEDERSEN 等[63]修正了WON溶解度参数的模型,提高了对固相非理想性的描述,将模型的应用范围从正构烷烃扩展到异构烷烃、环烷烃、芳香烃。WON 等[60]和HANSEN 等[62]溶解度模型在计算时认为固相热容和液相热容是相等的,但SCHOU 等[63]在计算时溶解度时未忽略固相和液相的热容差,在K 值模型中加入了固液相焓差修正项,计算结果更加准确。

ERICKSON 等[64]从三个方面对WON 等[60]模型进行了修正:一是根据组成分析划分了正构烷烃和异构烷烃两类物质,对正构烷烃和异构烷烃的熔点温度关联式分别进行了修正。二是对非均质固体混合物和原油组成进行热力学建模。三是调整模型的二元相平衡数据。适用于高压条件下的ERICKSON 等[65]模型需考虑三方面的因素:一是正构烷烃的熔点和浊点随压力增加而增加;二是轻组分、甲烷、乙烷和丙烷比用理想溶液预测的溶剂效果要差得多;三是石油烃在轻组分中的溶解度随着压力的增加而显著增加。

UNGERER等[66]提出用于描述非共结晶组分混合物的固液平衡热力学模型。Ungerer模型中的关联式可以适用于环烷烃,异构烷烃和芳香烃等其它烃类。假定所有组分以纯组分结晶,LIRAGALEANA 等[67]将该模型用于低压环境,而PAN等[68]将模型用于高压下并将适用范围扩展至原油。ZUO 等[69]考虑了Poynting因子对固相逸度的影响,用实沸点和石油重馏分的可调参数估算烷烃-环烷烃-芳烃的分布,该模型可在较宽压力范围内预测C7～C80油气体系固体析出温度和固体析出量。陈五花[70]根据结晶理论考虑了有序固相与无序固相之间的转换,结合正规溶液理论建立组分的固-固转换焓、固-固转换温度、熔化焓和熔点温度等新关系式。杨居衡等[71]首次将正规溶液模型和Wilson模型统一起来描述固相的非理想性,建立了IRSW 模型,模型对不同体系的固体析出温度均能得出准确的预测结果,平均相对偏差为0.19%,优于Pedersen的0.69%和P-Wilson的0.76%,对固体析出量的预测结果与实验数据接近,对不同温度下的固相碳数质量分布预测结果准确。

计算固相活度系数的方法有两种:一是基于正规溶液理论的活度系数模型;另一种是基于局部组成理论的活度系数模型。

表1总结了固相活度系数模型从原始到成熟期间的相关研究进展和模型的适用范围及优缺点。

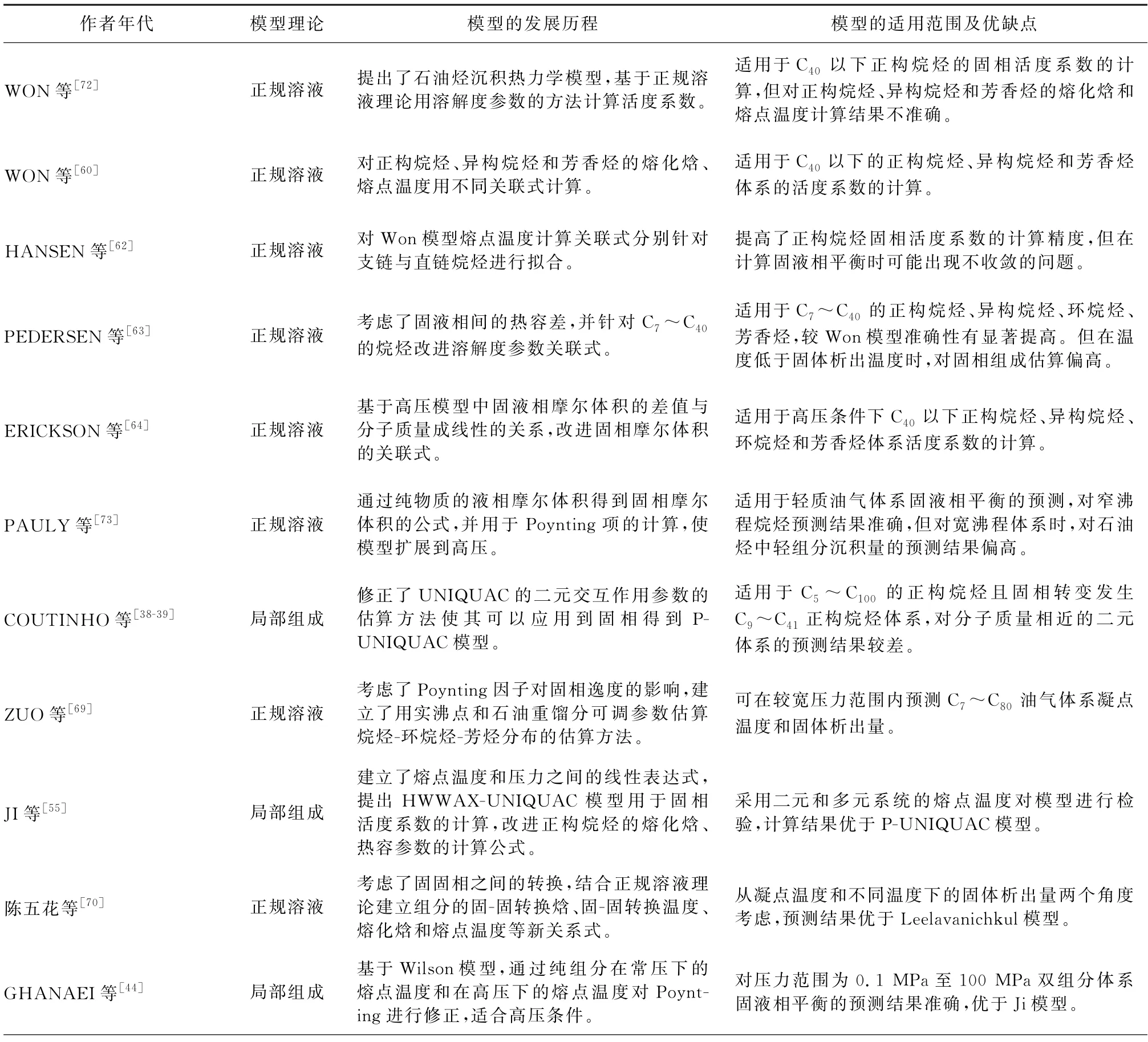
表1 固相活度系数模型的研究进展Table 1 Research progress of solid-phase activitycoefficient model

3 经验模型法

纯组分固体结晶时,固相活度系数为1,固相组成为1,通过计算纯组分固体在溶液中的溶解度即可进行固液相平衡的计算。常见经验模型有λh方程、Apelblat方程、Jouyban-Acree方程等。

3.1 λh 方程

BUCHOWSKI等[75-76]研究了苯酚和安息香酸在非极性溶剂中的溶解行为,找到活度、溶解度和温度的关系,导出二元体系溶解度模型,即λh方程,可采用两个参数预测多元体系中的固体溶解度。刘国柱等[77]将二元混合溶剂的组成参数增加到模型中,预测不同溶剂组成下的固体溶解度,扩大了λh方程的应用范围。但该模型用溶质在纯溶剂中的溶解度数据预测多元物系溶解度时不够准确。

贾青竹等[78]分别采用经验λh方程、Wilson、λh方程对2,4-二氯苯酚在水中的溶解度数据进行预测,λh方程预测结果最准确,平均相对偏差低于1.36%。骆健美等[79]测定了纳他霉素在不同比例水和甲醇混合溶剂中的溶解度,与实验结果比较相对误差小于6.76%。

3.2 Apelblat方程

APELBLAT 等[80]在常压下278 348 K 温度范围内测定了邻乙酰水杨酸、4-氨基水杨酸、3,5-二硝基水杨酸、对甲苯甲酸在水中的溶解度。根据固液相平衡原理,忽略溶质活度系数的影响,推导出溶解度与温度的关联式。假设溶液摩尔焓随温度呈线性变化,由Clausius-Clapeyron 方程推得溶解度随温度关系,简化得到Apelblat方程。

王勤波等[81]采用Apelblat关联式预测了不同温度下对苯二甲酸在不同浓度醋酸水溶液中的溶解度,预测结果的平均相对偏差为1.48%。张群艳等[82]测定了均四甲苯在9种纯溶剂中的溶解度,并分别用Apelblat、λh、NRTL、Wilson 4种模型进行了预测,其中APELBLAT 关联式的预测结果平均相对偏差最小,为3.47%。

3.3 Jouyban-Acree方程

Jouyban-Acree 方程由JOUYBAN 等[83]将CNIBS与Redlich-Kister方程结合,建立溶质在二元混合溶剂中的溶解度随温度与溶剂浓度的变化关系,得到Jouyban-Acree方程。Jouyban-Acree方程可用于二元或三元混合溶剂体系,还可以与Apelblat方程或Van't Hoff方程结合,用于预测不同温度下多元混合溶剂中的固体的溶解度。

田原铭等[84]测定了对乙酰氨基苯甲酸在甲醇和乙醇混合溶剂中的溶解度,Jouyban-Acree关联式预测结果的平均相对偏差为1.11%。陈高权等[85]用Jouyban-Acree关联式对硝基苯乙腈异构体在乙酸乙酯+甲醇、乙醇、正丙醇、异丙醇二元混合溶剂中溶解度预测结果的平均相对偏差小于为2.03%。

4 状态方程法

固液相平衡中,对于石油轻烃类体系,状态方程可以应用到固相,主要是求解固相逸度系数和液相逸度系数之比的问题,如式(3)。

4.1 PR模型

PENG 对SRK 方程做出了进一步的改进:在方程的引力项中进一步考虑了分子密度对分子引力的影响。经过大量数据的验算,可用于纯组分蒸气压的预测及弱极性化合物体系的相平衡计算,尤其可以得到液相摩尔体积的准确预测值。适用范围为非极性和弱极性化合物,在石油化工行业的相平衡计算中应用广泛。

向敏等[86]在原油中固相沉积相平衡中采用PR状态方程和SRK 状态方程描述液相的非理想性,结果表明,两种状态方程计算得到的固液相平衡结果非常接近。ABABNEH 等[87]在PR 状态方程中添加了经验关联式模型用来计算固相逸度系数,优化了交互作用参数,并预测了CH4-CO2-H2S 三元混合物的固液相平衡(5×105～30×105Pa,130～200 K),达到让CO2-H2S固相沉积的作用,当在较高压力和较低温度的条件下,固相中CO2和H2S 的分离效果达到了最优。MUKHOPADHYAY 等[88]改进了PR 状态方程,用一种新方法预测固液相平衡的固体溶解度,在这个方法中固体溶质在二元溶剂中的摩尔分数与溶剂的部分摩尔体积分数(一种溶剂对另一种溶剂加溶质混合物摩尔体积的贡献项)成正比,用改进的PR 状态方程关联了CO2-甲苯-萘三元体系的固液相平衡数据,平均相对偏差为3.11%。

4.2 SRK 模型

SRK 方程考虑了分子密度和温度对分子间引力的影响,引入了温度函数,特别是引入偏心因子,可使方程中的引力项随不同分子偏心力场变化加以调整,适用范围为非极性和弱极性化合物,在天然气和油气体系的PVT 计算中得到了广泛应用。

罗明检等[89]在原SRK 模型的基础上提出了新的α(T,ω),用于去优化模型计算纯物质的饱和蒸气压,并将改进后的模型与原模型在烃类、含氯有机物、含氟有机物、含氧有机物、无机物及水等37种纯物质1 447个点的饱和蒸气压进行预测,将平均相对偏差从2.521% 优化到1.673%。CARTER等[90]发现在公式(6)不能适用于高压体系,因为没有摩尔体积关于压力的积分项,同时也不适合增加Clapeyron项,CARTER 等[90]使用SRK 方程计算固液相之间的焓差和熵差,组建了新的求解液-固纯组分逸度比的公式,能够较好的预测甲烷-二氧化碳二元混合物的固液相平衡。

4.3 Martin-Hou模型

MARTIN 等[91]在Virial方程的基础上提出了多参数气体状态方程,根据PVT 关系求解出多参数状态方程系数的解析解,该方程具有准确度高,所需数据少,使用范围广,特别是能用于极性物质等优点。MARTIN 等[92]在MH-55 状态方程中增加了A5和C5两项系数,将方程的适用范围扩展到1.4ρc,并给出了A3、B3、C3、A5、B5、C5的求解方法,MH-55方程用于二氧化碳、水、苯、氮气、乙烷、硫化氢、丙烷时,最大偏差小于1%。侯虞钧等[93]修正了MH-55多参数状态方程,将其适用范围扩展到液相,MH-81方程是在MH-55 方程的基础上,在f4项中增加了B4项系数,提高了精算精度。侯虞钧等[94]MH-81方程在增加了3个常数A6、B7、bs后,使其适用范围扩展到固相,改进后的状态方程(MH-96)对于一般物质如二氧化碳、氩、甲烷及氮等,在三相点到临界点温度,计算饱和汽、液、固相摩尔体积,与实验值的偏差汽相小于1%,液相小于5%,固相小于5%。

5 结语

研究了固液相平衡模型,综述了活度系数模型、经验模型和状态方程模型。固液相平衡中液相逸度的计算,常压下采用活度系数法,高压下采用状态方程法;固相逸度的计算通过基于正规溶液理论或局部组成理论的活度系数模型及少数状态方程模型。

Pitzer模型适用于计算离子强度为6 mol以下强电解质水溶液体系的液相活度系数。ELECNRTL 精度比Pitzer 模型稍差一些,但ELECNRTL活度系数模型适用的浓度和研究对象范围更广泛。活度系数模型中Wilson方程计算精度较高,但Wilson方程不能用于部分互溶体系及活度系数有最大值的溶液。NRTL 三参数模拟下弥补了Wilson方程的不足,扩展了模型的应用范围。UNIQUAC计算精确度可与NRTL相比,且不需要非随机因子,拟合的参数对温度依赖性小,更适于外推应用。Coutinho改进基于局部组成理论的Wilson、NRTL和UNIQUAC方程,将其用于固相活度系数的计算。结果表明,对石油烃类体系固液相平衡的计算,基于局部组成理论活度系数模型的预测结果优于基于正规溶液理论的活度系数模型。λh和Apelblat经验模型适用于纯组分结晶的单溶剂体系,而Jouyban-Acree经验模型适用于纯组分结晶的二元到三元混合溶剂体系。PR 和SRK 状态方程模型通常用来描述石油轻烃类体系的固液相平衡中液相的非理想性,MH-81和MH-96方程分别用来计算二氧化碳、氩、甲烷及氮等体系的固液相平衡中的饱和液相和固相摩尔体积。

通过对固液相平衡中活度系数模型、经验模型和状态方程模型的分类分析,为不同体系固液相平衡计算模型的选择和应用提供指导和帮助,具有一定的实用价值和指导意义。

符号说明

x i,L、x i,S——分别为组分i在液相和固相中的摩尔分数

i,L、γi,S——分别为组分i在液相和固相中的活度系数

f i,L（T,P）、f i,S（T,P）——分别为在温度T和压力P的条件下纯液态组分i和纯固态组分i的逸度

ΔG i,SL——纯组分由固态变为液态时的Gibbs自由能变化,可以由焓变和熵变得到

f i,SO——纯固态组分i在参考压力P0下的逸度

γi,SO——常压P0下固体相中组分i的活度系数

f i,LO——纯液态组分i在参考压力P0下的逸度

φi,LO——纯液态组分i在参考压力P0下的逸度系数

T i,f——组分i的熔点温度,K

ΔH i,f——组分i的熔化焓,J·mol-1