借助“穿越”情境 展开想象与操作

杜梦琳

【摘   要】在故事情境中展开想象与操作是发展想象力的重要策略。教师可以用“图形运动会”的故事情境为载体，通过“对接生活经验、依托想象说理、动手操作验证、故事情节助推、联结知识结构”等过程，引导学生探究“三角形的高”，帮助学生积累数学活动经验，发展空间想象力。

【关键词】三角形的高；图形想象；操作活动

在“三角形的认识”中，边和角是三角形的显性特征，高则是隐性特征。正确找到高，感受三角形底和高的相互依存关系，需要较强的空间想象力。因此，借助“三角形的高”这一内容，可以帮助学生积累数学活动经验，发展空间想象力。

一、课前思考

在认识三角形之前，学生已经学习了垂直关系，理解了“点到直线的距离”，具备了对距离概念与最短线段等的感性认识，掌握了过指定点画已知直线的垂线的作图技能。在日常生活中，也常常会遇到诸如测量身高之类的“测高”活动。因此，学生已具备学习三角形的高的经验基础。

在“三角形的高”的教学中，教师一般会采用讲授法，将三角形的高直接告知学生，让他们从认识概念直接到应用概念。这个教学过程忽视了学生的直接经验，致使学生难以理解认识三角形的高的本质及必要性。另外，在教学实践中，画高对学生而言也有一定难度，特别是画直角三角形的高和钝角三角形的高。

基于上述分析，笔者设计了“图形运动会”的故事情境，推动学生主动探究，在猜高、画高、量高、试高、比高等活动中展开对三角形的高的学习，从而理解三角形的高的本质，发展空间想象力。本内容的具体教学目标如下。

（1）通过思考三角形的穿越策略，主动构建三角形的底和高之间的联系，为操作提供想象基础。

（2）通过观察锐角三角形、直角三角形和钝角三角形等三角形模型穿门的过程，直观感知高的位置与长短，为探索三角形的高的本质提供直接经验。

（3）通过对各类三角形的高的观察、对比和思考，建立结构化思维，进一步提高想象力。

二、教学实践

（一）对接生活经验，丰富表象感知“高”

真实情境与问题提出有助于推动学生主动参与教学活动。学生学习的起点是生活中的一些实际事例，学习数学的过程是对现实经验的理解与反思过程［1］。在故事中融入数学问题，能激发学生的数学想象力以及他们提出问题的能力。

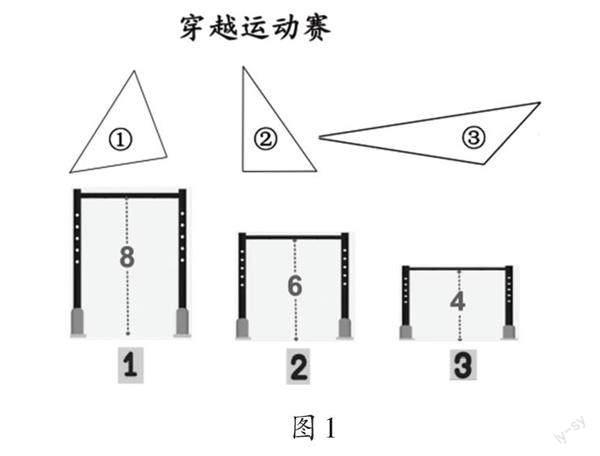
教学时，教师结合杭州亚运会，以小视频的形式引入“图形运动会”的故事情境：有3名三角形运动员准备参加“穿越运动赛”，只要穿过一道幸运门就能获得1枚奖章（如图1）。

师：比赛前，大家先来预测一下这3名三角形运动员的获奖情况。

生：①号运动员看上去能穿过两道门，能得2枚奖章。

生：②号运动员看上去有点高，只能穿过1号门，得1枚奖章；③号运动员最矮，能得3枚奖章。

生：②号运动员只要翻个身就能穿过三道门，能得3枚奖章。

生：如果可以翻身，那么每名运动员都可以获得3枚奖章。

学生通过观察，一一比较三扇门的门高与三角形运动员的身高，并提出设想：三角形有三条边、三个顶点，若以不同的边为底，那么三角形的“身高”各不相同。

设计意图：在学习三角形的高之前，学生已经积累了对“高”的认识。因此，学生学习三角形的高时能自然对接原有的测身高经验，激活对高的直观感知。教师创设“图形运动会”的故事情境，让学生通过观察，想象三角形的高就是三角形运动员“头顶”（顶点）到“脚底”（底边）之间的距离。这样的学习方式符合学生天真活泼爱幻想的天性，拟人化的方式也有助于学生建立不同事物间的关联以开启想象。

（二）依托想象说理，动手探究辨析“高”

问题提出后，教师要引导学生充分联想、自由表达，在应用直接经验的基础上进行辨析、探究，生成学习资源，有效促进学生从感性认识上升到理性认识。

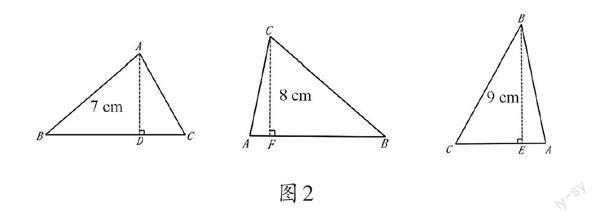
由于每名学生对锐角三角形的高的想象都是不同的，因此，教师让学生基于想象，借助学习单来寻找锐角三角形的高，并在锐角三角形上画一画、量一量高的长度（如图2）。

学生通过交流反馈，体会到高是三角形的顶点到对边的最短距离，是一条垂线段。

设计意图：以三角形非水平方向的边为底作高是学生学习的难点。教师先利用三角形运动员穿越幸运门的故事情境，引导学生展开想象，思考三角形运动员可以通过改变站姿来适应门高，从而认识锐角三角形三条不同的高。然后鼓励学生想象与说理，明晰三角形高的概念本質，丰富对三角形三条高认知的经验。

（三）动手操作验证，推动对“高”的深刻想象

操作活动需要思维的参与，思维也需要在操作活动中发展，想象力的发展离不开操作活动［2］。带着想象进行操作活动，学生就能形成明确的研究目标，用数学的思维理解现实图像的数学意义。

在学生画锐角三角形的高的基础上，教师提供学具（如图3），组织学生进行操作验证：“准备好了吗？请锐角三角形运动员上场！”让学生用锐角三角形学具进行穿越实验，验证其是否能穿过图中的三道门。

学生在操作中发现：锐角三角形只能用两种“站姿”穿过1号门，即能以两条较短的高穿过1号门，但穿不过2号和3号门（如图4）。因此，锐角三角形运动员能获得1枚奖章。

设计意图：本环节立足操作与想象，使学生获得对三角形的高的直观感知。教师让学生用三角形学具和门框模型模拟比赛现场，通过直观操作，将三扇门的门高与三角形运动员的身高进行一一比较，看到结果后验证自己的想象，形成想象回路，体会“顶点”“对边”“垂线段”的深刻内涵。

（四）故事情节助推，对不同“高”进行充分想象

理解直角三角形、钝角三角形的高是教学的难点，因此，教师要让学生依托视觉、触觉等感官活动，将产生的直觉感知与想象进行互动，从而形成清晰的表象。

教师为每组学生提供直角三角形（三条高分别为8 cm、6 cm、5 cm）和钝角三角形（三条高分别为8 cm、4 cm、3 cm）学具（如图5），组织学生继续进行操作验证：直角三角形和钝角三角形运动员分别能获得几枚奖章呢？学生可以在学习单上画高、量高，或直接在三角形学具上量高。

学生完成探究后，教师组织反馈。

师：这两名三角形运动员到底有多高呢？它们的高在哪里呢？

生：（呈现学习单上的直角三角形作高图）直角三角形有两条直角边，一条直角边作底时，另一条直角边就是它的高。这样的高有两条，分别为8 cm和6 cm，还有一条是以斜边为底作的高，为5 cm。直角三角形无论用什么“站姿”都能穿过1号门，可以得到1枚奖章。

生：2号门的高度是6 cm，3号门的高度是4 cm。直角三角形能够穿过2号门，但穿不过3号门，因此还可以再得1枚奖章。

生：（呈现钝角三角形作高图）我觉得钝角三角形运动员很特别，它只有一条高在三角形内部，长3 cm，另外两条高好像不在三角形内。大家看，当钝角三角形的顶点碰到门框时，可以看到它的高在三角形外（如图6、图7）。

生：是的，我也发现了。钝角两边张开的角度大，所以有两条高在外面。

图形外面的高能画出来吗，怎么画？教师因势利导，示范画钝角三角形的外高。

学生讨论总结直角三角形高的位置特征和画图技巧：两条直角边互为底和高，用斜边作底对应一条内高。作图时，与两条直角边重合的高不用重复画，加直角符号即可。钝角三角形有两条外高和一条内高。画外高时，要先将底边延长，再过顶点作高。

设计意图：锐角三角形的三条高都是内高，直角三角形有两条直角边互为底和高，钝角三角形有两条外高。其中，钝角三角形的两条外高是难点，学生很难想象。因此，教师要给学生提供学具，让学生借助实物模型进行探究，有物可比，有形可想。经过反复操作，学生打破固有想法，意识到高确实会落在钝角三角形的外部，高虽“无形”却真实存在，有效突破了钝角三角形“外高”的认知难点。

（五）联结知识结构，拓展对“高”的想象深度

数学知识具有内在联系的结构化特征。教学中，教师要利用学生已有知识，引导学生辨析学习材料，进行联想推理，形成结构化思维，培养空间想象力和空间观念。

教师引导学生思考：在三角形ABC中，如果BC边不变，将顶点A左右移动，高会发生什么变化？三角形会发生什么变化？在学生想象的基础上，用视频进行动态演示，帮助学生理解：锐角三角形的高在三角形内部，直角三角形的高在直角边上，钝角三角形的高在三角形外部。由此为后续学习三角形面积奠定基础。

设计意图：通过左右移动顶点A，激发学生的动态想象，让学生感受高的位置变化带来三角形形状的变化，进一步丰富学生对高的认识。同时让学生感受到：虽然三角形高的位置有变化，但它们有共同的底和相等的高。由此为后续学习三角形面积奠定基础。这一环节的教学加深了学生对三角形高的本质的认识，使学生在想象三角形高与形状发生变化的过程中，培养空间观念和想象力。

三、教后所思

（一）以故事为载体，激发数学想象

数学故事可以成为承载数学知识和数学问题的载体，触发学生的情感投入，激发学生的想象力。本内容的教学基于学生生活中的测高经验展开，并与杭州亚运会相结合，通過创编“图形运动会”的故事情境，让学生在故事情节中思考：三角形的高在哪里？哪种三角形的高最矮？研究三角形的高有什么用？等等。

（二）以猜想为导向，引领数学想象

著名数学家波利亚说过：“数学既要教证明，又要教猜想。”猜想不是天马行空地乱想，而是要有一定的科学依据和针对性［3］。教师要让学生在想象中提出猜想、合理推导，并操作验证。首先，创设3名三角形运动员参加“穿越运动赛”的故事情境，让学生通过观察进行直觉猜想：各个三角形运动员都能穿过哪些门？接着，帮助学生给锐角三角形画高、量高，理解“高是三角形的顶点到对边的最短距离，高是一条垂线段”。最后，在学生猜想的基础上，引导学生用实物操作验证。在反复操作中，学生展开深度思考：顶点和底为什么要对应呢？为什么作高要作垂线段呢？由此引导学生主动建构三角形高的概念。该教学设计借助学生的猜想，让学生顺利完成从“物”到“形”的转换，由此发展学生的空间想象力，逐步培养学生的空间观念［4］。

（三）以操作为依托，助推数学想象

数学想象要有清晰表象作为经验素材。为突破钝角三角形的形外高这个教学难点，教师要让学生展开对三角形的高的本质的数学洞察。学生在对数学形式化材料的操作中，感知高不取决于三角形的形状与位置，而只取决于顶点与底之间的距离。动手操作是探究的开始，观察生成想象，想象又促使学生提出数学问题，探究数学规律。

在本内容的教学中，学生在创编故事的活动体验中，将数学问题转化为具体的实践问题，将生活经验内化为数学概念，收获了有趣的数学学习体验和丰富的想象力。

参考文献：

［1］史宁中，曹一鸣.义务教育数学课程标准（2022年版）解读［M］.北京：北京师范大学出版社，2022.

［2］颜秀敏.借力想象 积淀素养：小学数学课堂如何培养学生的想象能力［J］.学苑教育，2022（7）：12-13，16.

［3］费正蕾.先致其知 致知雕琢：带着学生学习需求走进数学课堂［J］.学苑教育，2015（11）：59.

［4］顾卫华.数学想象，让儿童“破茧飞翔”［J］.数学大世界（下旬），2018（11）：44.