项目化学习的理解与活动设计

卢立涛　马颢文　朱晓晴

【摘   要】项目化学习是一种凸显学生主体性的学习方式，它以真实情境中产生的、具有挑战性的问题为驱动，引导学生综合运用学科知识开展探究活动，在实践探索过程中实现知识的建构。教师以人教版教材五年级上册“多边形的面积”单元为例，组织开展数学项目化学习，引导学生在真实情境中，探索驱动性问题的解决方法，提升学生的几何直观和空间观念，发展学生的核心素养。

【关键词】项目化学习；小学数学；多边形的面积；活动设计

一、研究背景

项目化学习作为一种凸显学生主体性的学习方式如今备受推崇。研究表明，参与过数学项目化学习的学生，其数学表现要优于没参与过的学生，项目化学习有助于学生综合数学素养的培养［1］。近年来，我国对项目化学习的理论与实践的探索也在不断深入。《义务教育数学课程标准（2022年版）》（以下简称“2022年版课标”）就强调要“以跨学科主题学习为主，适当采用主题式学习和项目式学习的方式，引导学生综合运用数学学科和跨学科的知识与方法解决问题”。

项目化学习以真实情境中产生的、具有挑战性的问题为驱动，引导学生综合运用学科知识开展探究活动，在实践探索过程中实现知识的建构。项目化学习能改善传统课堂中知识碎片化、学生难以迁移运用知识解决实际问题等困境。因此，在数学课堂中引入项目化学习方式，有利于培养学生在真实情境中综合运用知识解决实际问题的能力，符合当下指向发展学生核心素养的教学改革的大趋势。

教师应以2022年版课标为核心，以小学数学学科教学为主阵地，组织学生开展数学项目化学习［2］。通过梳理课程内容，从中发掘真实情境中的问题，设计有价值的学习任务，从而使学生学会用数学的眼光观察生活、用数学的思维解决实际问题、用数学的语言表达现实世界。

二、项目化学习实践

基于上述背景，笔者以人教版教材五年级上册“多边形的面积”单元的教学为例，设计并组织开展数学项目化学习，以培养学生的数学核心素养。

2022年版课标指出，几何直观与空间观念是小学阶段核心素养的两个主要表现，在第三学段（5～6年级）具体体现为：探索几何图形面积和体积的计算方法；尝试在真实情境中发现和提出问题；运用几何直观和其他学科的知识、方法分析和解决问题，形成初步的应用意识和创新意识。“多边形的面积”单元是“图形与几何”领域的重要学习内容，以本单元的教学内容为载体开展项目化学习，有利于培养学生的几何直观与空间观念。

基于前人的研究成果和实际教学情况，本单元的项目化学习流程可分为四个步骤：一是分析项目选题与教学目标；二是设计驱动性问题；三是设计活动过程，即具体课时安排；四是开展项目教学成果评价。

（一）分析项目选题与教学目标

该环节的主要内容是基于2022年版课标中有关数学学科核心概念与核心素养的要求，结合教材内容与学生经验，分析项目选题与教学目标，选择适合开展项目化学习的组织形式。

教师在解读2022年版课标的基础上，通过分析教材与学情，确立如下单元教学目标：（1）学会从真实情境中抽象出多边形，利用割补法发现三角形、平行四边形、梯形之间的关系，并用此方法计算简单组合图形的面积，培养几何直观和空间观念；（2）掌握平行四边形、三角形和梯形的面积公式，并能正确地计算平行四边形、三角形和梯形的面积；（3）学会运用转化的数学思维，经历平行四边形、三角形和梯形面积公式的推导过程；（4）在解决问题的过程中，感受数学和现实生活的密切联系，体会学习数學的乐趣。

为贴近学生的日常生活，教师将本单元项目化学习的活动主题设定为“校园绿植美化问题”，引导学生代入校园美丽环境的“设计者”和“建设者”的角色，设计一种既符合预算，又能够在有限空间中建造出具有美感的花坛的种植方案。学生在三年级已学习过长方形面积的计算，并初步认识了三角形、平行四边形等图形，但尚未掌握相关图形的面积计算。此项目选题能充分激发学生的潜能，帮助他们学会运用多边形面积公式解决生活中的实际问题。

（二）设计驱动性问题

通过创设真实问题情境，可以将本质问题分解为两个驱动性问题。驱动性问题贯穿于整个项目，需要适合五年级学生的年龄特征和认知特点，以调动学生的学习积极性；还要具有开放性，让学生可以进行个性化作答。

◆本质问题

如何计算多边形的面积？如何计算组合图形的面积？

◆问题情境

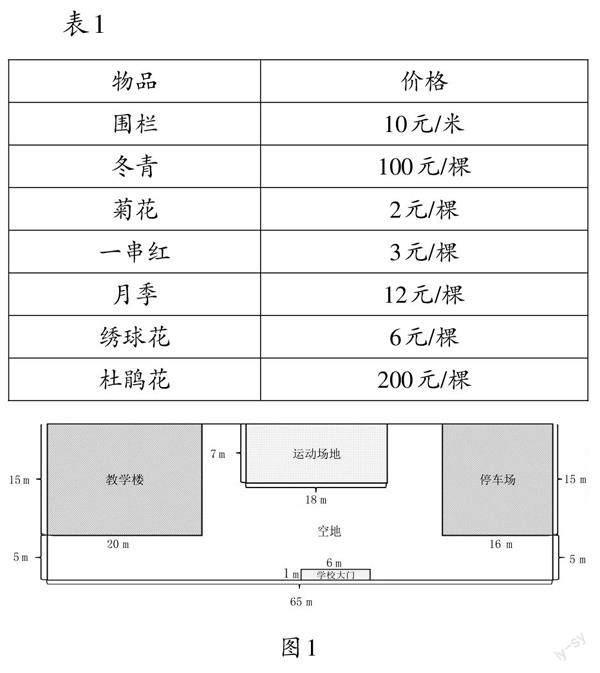
临近五一劳动节，学校准备在教学楼前的空地上建造一座花坛，对校园进行美化。故向学生发出设计邀请，请学生设计一份符合设计要求的方案。设计要求：由于空地大小和学校经费有限，花坛的面积和形状要符合实际情况，每种设计方案的总费用不得超过5000元；为了美观，花坛内绿植的种类要尽可能丰富，并要有一定的图案设计；此外，花坛外侧还需有围栏环绕。为方便大家设计、计算，学校提供了建造花坛所需物品价格表（如表1）和校园平面图（如图1）。

◆驱动性问题

以小组为单位展开讨论，提出符合上述条件的设计方案，计算出所需费用，并展示小组设计图，说明设计理由。这一学习任务具体可分解为两个驱动性问题：（1）花坛面积是多少？（2）建造花坛一共需要多少费用？

（三）设计活动过程：具体课时安排

为了突出学生的主体性，提高他们的课堂参与度，本项目化学习以小组合作为主要的学习形式，计划用时4课时，具体安排如下。

◆第1课时：创设真实情境，学习平行四边形和三角形面积的计算

（1）创设真实情境。教师呈现部分花坛图片（如图2、图3），引导学生观察各式各样的花坛形状。通过创设真实情境，让学生发现花坛可以是基本图形（如长方形、平行四边形、三角形等），也可以是组合图形，激发学生的想象力，发展学生的几何直观和空间观念。

（2）进行分组设计。教师遵循“同组异质，异组同质”的原则给全班学生分组，要求各组在方格纸上设计花坛形状，并用数方格的方法计算花坛面积，限时5分钟。由于学生尚未掌握多边形面积计算的知识，在画图的过程中会发现，平行四边形、三角形等多边图形的面积难以通过数方格的方式计算。为解决这些问题，他们自然会产生探索多边形面积公式的想法。

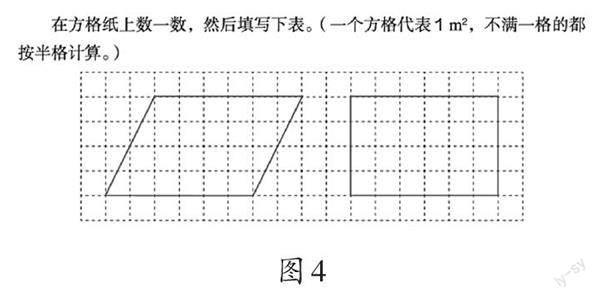
（3）提出第一个驱动性问题：花坛面积是多少？学生设计花坛时，可能会绘制平行四边形、三角形、梯形等各种图形。教师可以借助部分小组设计图中的平行四边形，引导学生探索平行四边形面积的计算，学会采用数方格的方式计算平行四边形的面积（如图4）。学生通过同时数一个长方形和一个平行四边形的面积，对它们的底（长）、高（宽）和面积进行比较，为进一步探索平行四边形面积的计算方法做准备。

（4）推导平行四边形、三角形的面积公式。教师引导学生采用动手操作、自学课本、小组讨论等学习方式，用割补法将平行四边形转化为长方形（如图5），通过观察转化前后两个图形之间的等量关系，推导出平行四边形的面积计算公式：

平行四边形的面积=底×高，即S=ah。

接着，启发学生连接对角线，引导学生发现三角形的面积是与它同底等高的平行四边形面积的一半，从而在平行四边形面积计算公式的基础上，得出三角形的面积计算公式：

三角形的面积=底×高÷2，即S=ah÷2。

◆第2课时：梯形与组合图形的面积计算

（1）探索梯形的面积公式。引导学生利用第1课时学到的割补法，探索两个相同的梯形可以拼成一个平行四边形（如图6）的操作方法。

从而得出梯形的面积计算公式：

梯形的面积=（上底+下底）×高÷2，即S=（a+b）h÷2。

（2）探索组合图形的面积计算方法。在学生掌握了平行四边形、三角形、梯形的面积计算公式后，引导学生进一步探索由多种图形组合而成的花坛的面积。

◆第3课时：绿植种类挑选与绿植占地面积计算

（1）提出第二个驱动性问题：建设花坛一共需要多少费用？各组需先确定花坛的形状、大小是否合适，然后设计不同种类绿植的组合种植方案，确定绿植的种类和数量，从而计算出花坛建设所需的总费用。

（2）探索解决“一定面积内，能种多少棵绿植”的问题。要解决这一问题，学生需要思考绿植之间的间隔距离及不同绿植的占地面积。为合理安排不同绿植间的种植距离，教师要让学生先自主学习生物学的相关知识，再通过小组合作，了解树冠的大小，光照、养分的供应情况。在设计具体方案时，教师为学生提供了不同种类绿植占地面积的信息（如表2），启发学生：从绿植生成的角度，每棵绿植的空间不应小于表中数据；从种植美观的角度，绿植的间隔不宜过大。另外，表中涉及不同的面积单位，计算时需统一单位。此环节旨在帮助学生掌握用面积计算绿植数量的方法，培养学生面积单位换算、资料收集分析的能力，以及数学和生物学科的跨学科素养。

（3）各组根据设计方案和预留的绿植占地面积，确定绿植的种类和数量，计算所需费用，最后商讨确定最佳方案。

◆第4课时：方案展示与讨论总结

（1）各组轮流展示设计方案，讲解花坛的形状、面积，选择的绿植种类、数量，所需的费用以及设计意图。

（2）采取学生互评和教师点评的多元评价方式进行评分，引导学生倾听他人的观点表达，进行自我反思，改进设计方案。

（3）从花坛面积大小是否符合空地情况、花坛设计是否美观、项目进展过程中的小组分工合作情况等多个方面，对各组的设计方案进行总结评价。

（四）开展项目教学成果评价

项目成果是对学生进行评价的重要指标之一。各组需要在全班同学面前展示项目成果，并进行讨论与评价。项目成果分为个人成果和团队成果，个人成果为理解、掌握多边形面积及组合图形面积的计算方法，团队成果指团队分工合作共同完成设计方案。项目成果的评价标准为：会进行面积单位换算；能够熟练地运用多边形面积计算的知识与方法解决生活中的实际问题；能发展空间观念和几何直观，学会用数学的语言进行表达。

三、总结与反思

（一）真实情境凸显学生学习的主体性

数学源于生活，用于生活。本项目化学习围绕“校园绿植美化问题”这一主题，鼓励学生以校园绿化的“设计者”和“建设者”的角色参与校园花坛设计活动，让学生通过数学与艺术构思，在小组合作讨论中形成不同形状、不同绿植组合，且又符合预算的花坛设计方案，从而提升学生的校园归属感与环境意识。

（二）驱动性问题促进学生学习的一致性与连贯性

本项目化学习将抽象的本质问题转化为两个具体的驱动性问题贯穿于整个项目，分别在不同阶段起到关键的推动作用。第1、2课时集中解决第一个驱动性问题“花坛面积是多少？”强调数学基础知识的学习。在课堂中，教师通过数方格法、割补法，帮助学生在“做中学”，从而让学生学习平行四边形、三角形和梯形的面积计算公式。第3、4课时主要指向第二个驱动性问题“建设花坛一共需要多少费用？”注重综合能力的培养。教师在前两个课时的基础上提升难度，让学生综合考虑多方面因素，挑选合适的绿植种类，计算绿植占地面积以及费用。不过，学生在设计花坛形状的过程中，可能会画出除本单元学习的几种图形以外的其他多边形或不规则图形。遇到这类情况，教师应充分利用课堂的生成性资源，拓展教材内容，引导学生将此类图形转化为已知图形，利用公式准确计算或估算出面积。

综上，该项目化学习巧妙地将实际生活与教学内容相结合，挖掘数学知识的生活内涵，让学生深刻体会到数学就在身边，感受到数学的魅力和学习数学的乐趣，能够灵活应用多边形面积计算方法解决生活中的实际问题。在该项目化学习过程中，以数学学科为依托，整合生物、美术等其他学科，提升了学生的综合能力与学科核心素养。今后设计项目化学习时，教师要更加注意与学生经验、资源等的匹配度，经常性进行自我反思，积极接受培训，提高自身的专业素养，以此推动实践活动，培养学生的数学核心素养。

参考文献：

［1］GRANT M M，BRANCH R M. Project-based learning in a middle school：Tracing abilities through the artifacts of learning［J］. Journal of Research on Technology in Education，2005，38（1）：65–98.

［2］庄治新，陈雪飞.基于核心概念的数学项目化学习设计［J］.教學与管理，2019（32）：43-45.

*本文系“十四五”规划2021年度教育学一般课题“建党以来中国特色教研制度变迁逻辑及教研员循证发展路径研究”（课题编号：BHA210128）的研究成果。