极值点偏移问题的典型方法剖析

蔡晓纯

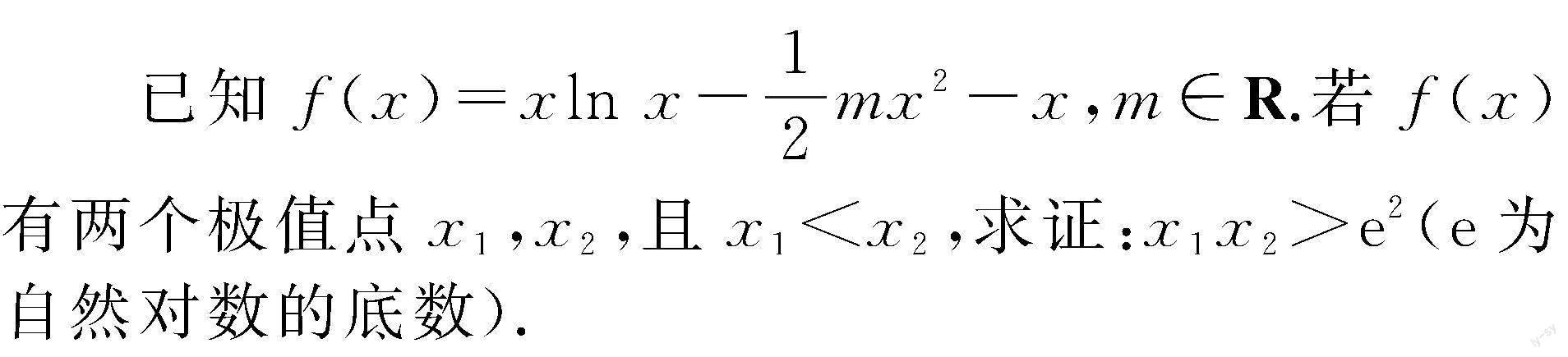
摘要：所谓极值点偏移问题，是指对于单极值函数，由于函数极值点左右的增减速度不同，使得函数图象没有出现对称性.此类问题是导数题型中的热点问题，常以压轴题的形式出现.本文中从一道例题出发，分析学生在解极值点偏移问题时常犯的典型错误，并给出该类问题的常见解法.

关键词：极值点偏移问题；解法探究；方法总结

极值点偏移问题是高考中常出现的一类导数问题，难度大，技巧性较强，学生在解决此类问题时经常出现不求甚解地构造函数所造成的解题错误［1］.下面结合一道例题，对解题中需要注意的事項进行剖析.

1 例题呈现

简析：f′（x）=ln x-mx，记g（x）=ln x-mx，由题意知x1，x2是f（x）的两个极值点，故x1，x2是g（x）的两个零点.

2 学生常见的解题思维受阻分析

2.1 不明确极值点

（1）受阻原因

（2）修正后的方法

2.2 未明确偏移方向

（1）受阻原因

（2）修正后的方法

评注：方法一和方法二均是利用构造的新函数来达到消元的目的，本质上是为了将双变元不等式转化为单变元不等式.事实上，还可以通过构造新变元，将两个旧变元都换成新变元来表示，从而达到消元的目的.

3 另外两种方法欣赏

参考文献：

[1]荣兵.探讨极值点偏移问题[J].高考，2021（30）：150-151.

[2]李荣.解答函数极值点偏移问题的两种方法[J].语数外学习（高中版下旬），2022（1）：56.