洞悉高考考题方向 加强试题融旧创新
2023-11-25周毅鸿周建玲彭国富
周毅鸿 周建玲 彭国富


新高考强调基础性、综合性、应用性和创新性,在试题之间、考点之间、学科之间相互关联,交织成网,对学生素质进行全面考查.通过对2022年全国数学新高考Ⅱ卷考题的分析发现,考题在呈现方式和设问方式上有所创新,打破了一些固有模式,以此考查学生解决问题的应变能力和创新能力.如何引导学生建立起必备知识与关键能力、学科素养、核心价值之间的紧密联系,这需要教师高屋建瓴,善抓典型例习题、考题中的核心知识与方法并进行融旧创新的改编,以培养学生在新情境下积极主动地探索新方法解决问题的创新能力.下面将重点以例1的第(3)问为例,逆向论述一些常规解题与试题融旧创新的实践研究.
1 試题呈现与简要分析
例1 (2022年全国数学新高考Ⅱ卷第22题)
已知函数f(x)=xeax-ex.
(1)当a=1时,讨论f(x)的单调性;
(2)当x>0时,f(x)<-1,求实数a的取值范围;
(3)设n∈N*,证明:
分析:第(1)问求导,令导函数大(小)于0较易解决;第(2)问是恒成立问题,可分离参数.由f(0)=-1,猜想它是一个端点效应问题,可试着分类讨论.第(2)问的具体解答过程如下.
解析:(2)求导,得f′(x)=eax(1+ax-ex-ax)(x>0).
令φ(x)=1+ax-ex-ax,则φ′(x)=a+(a-1)\5ex-ax,可得φ′(0)=2a-1.
当a≥1时,φ′(x)>0,则φ(x)在(0,+∞)上单调递增,
φ(x)>φ(0)=0,即f′(x)>0,所以f(x)在(0,+∞)上单调递增,f(x)>f(0)=-1,不满足题意.
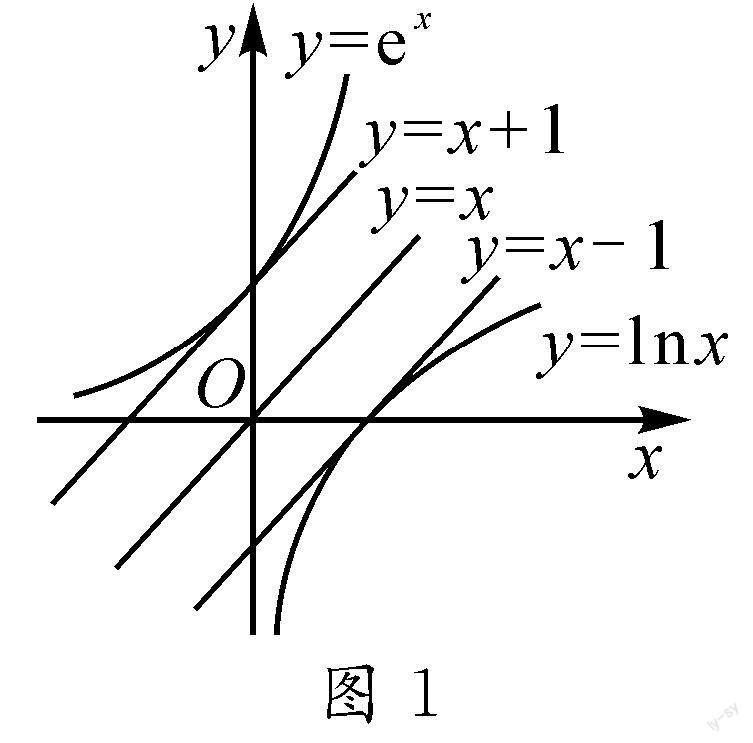
0,即f′(x)<0,所以f(x)在(0,+∞)单调递减,f(x) 关于第(2)问的解法探究,常见的还有几种,本文中不一一呈现.下面重点探究例1的第(3)问.师生普遍感到第(3)问很难,并且参考答案也有些突兀、难以理解. 2 破难寻质 例1的第(3)问巧妙地将函数、导数、数列、不等式结合在一起,体现了新高考以必备知识为基础,强调各个知识点之间相互关联,同时也突出了问题呈现方式的新颖性.在对第(3)问的破题过程中,笔者联想到了平时教学研究中的两个经验. 2.1 联想一 首先联想到了下面例2的第(2)问: 例2 (2019年东北四校联考)若函数 f(x)=ex-ax-1(a>0)在x=0处取极值. (1)求a的值,并判断该极值是函数的最大值还是最小值; 2.2 联想二 2020年人教A版新教材选择性必修第二册习题5.3的第12题: 利用函数的单调性,证明下列不等式,并通过函数图象直观验证: (1)ex>1+x(x≠0);(2)ln x 由此题的(1)(2)可推出以下基本模型.在教学中,也可引导学生画如图1所示的函数图象,帮助学生更好地理解基本模型[1]: ①ex>1+x(x≠0); ②ln x ③ln x ④ln(x+1) 于是,可得到例2(2)的解题思路: 3 源质破难 4 总结反思 综观例1第(3)问的解题思路,虽然形式新颖,但万变不离其宗.在高考复习阶段,教学中不仅要讲清楚题目本身及其变式训练,还要引导学生“揭示问题本质”,通过“本质”去编题、命题,打破机械刷题、机械套路.为了不让学生盲目地刷题,教师要通过对试题的核心知识与方法的融旧创新,时时引导学生主动思考问题,在“生”中寻“熟”,灵活运用各种知识与思想方法.真正通过数学教育,帮助学生形成理性思维、科学精神,促进其个人智力发展,发挥数学学科不可替代的作用. 参考文献: [1]周毅鸿,周建玲,洪竟雄.巧用基础模型,拎起导数骨架[J].中学数学,2020(23):64-65.
