基于数据分析，培养核心素养

许润玲

摘要：结合教学实际，从图形直观、数表信息、性质特征以及创新定义等方面例析数据分析的具体应用，培养与渗透数据分析核心素养，提高数学应用能力.

关键词：数据分析；核心素养；圖形；数形；创新

数据分析作为大数据时代数学应用的主要方法，是概率与统计学习中的一种基本方法，也是数学学科的一个基本素养.在数学教学过程中，基于数据分析，通过数据的收集和整理，提取信息，构建模型，进行推断，形成关于研究对象的知识与判断，用于合理决策相关问题.通过这一教学过程，培养学生的数据分析等核心素养.

1 基于图形直观进行数据分析

通过对概率与统计中图形（频率分布直方图、折线图、饼图等）的识别，提取相关的数据信息，进而加以合理数据分析与应用.

例1 〔2023年浙江省绍兴市嵊州市高考数学质检试卷（2月份）〕某中学为了解高三男生的体能情况，通过随机抽样，获得了200名男生的100米体能测试成绩（单位：s），将数据按照[11.5，12），[12，12.5），……，[15.5，16]分成9组，制成了如图1所示的频率分布直方图.

由直方图可估计本校高三男生100米体能测试成绩小于13.5 s的人数为（）.

A.47

B.54

C.67

D.94

分析：根据题设条件，先由频率分布直方图中各长方形的面积之和为1求得参数a的值，再结合频率分布直方图的直观性，从中提取相应的数据信息加以数据分析，进而求解本校高三男生100米体能测试成绩小于13.5 s的人数即可.

解析：由频率分布直方图中各长方形的面积之和为1，

可知0.5×（0.08+0.16+0.30+a+0.52+0.30+0.12+0.08+0.04）=1，解得a=0.40.

故估计本校高三男生100米体能测试成绩小于13.5 s的人数为200×0.5×（0.08+0.16+0.30+0.40）=94.

故选择答案：D.

点评：在解决一些涉及概率与统计中图形信息的问题时，关键是借助直观性，从概率与统计的图形中正确提取出对应的数据信息，结合相关的数学知识加以数据分析，合理数学运算或逻辑推理，巧妙转化与应用，实现合理数据分析与数据处理的目的.从图形中正确提取相关的数据信息，是解决问题的关键所在.

2 基于数表信息进行数据分析

通过对概率与统计中的数表的分析，确定相关的数据信息，进而加以合理数据分析与应用.

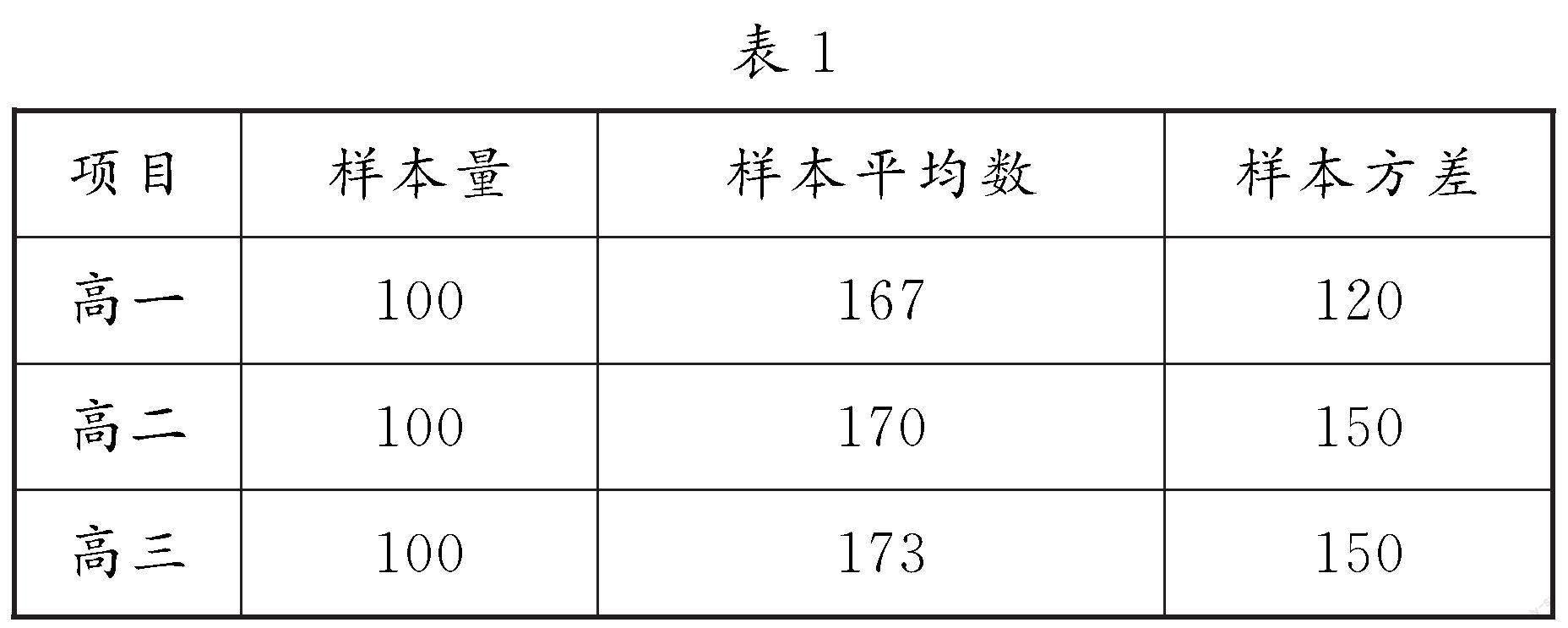
例2 （2023届湖北省武汉市武昌区高三年级质量检测数学试卷）某校采用分层随机抽样的方法采集了高一、高二、高三年级学生的身高情况，部分调查数据如表1：

则总样本的方差为.

故填答案：146.

点评：处理此类问题时，根据数表信息获取数据，并结合平均数与方差的公式加以分析与计算，进而得以合理数据分析与决策判断.本题结合实际应用问题，合理利用分层抽样的平均数公式与方差公式是解决该问题的关键所在.

3 基于性质特征进行数据分析

通过概率与统计中相关公式、关系式等的应用，获得相关的数据信息，进而加以合理数据分析与应用.

A.这次测试的平均成绩为90

B.这次测试的成绩的方差为10

C.分数在110分以上的人数与分数在80分以下的人数相同

D.分数在120分以上的人数与分数在60分以下的人数大致相同

分析：根据题设条件，利用正态密度曲线所对应的函数关系式，基于关系式的性质特征，确定正态分布的平均值μ，标准差δ的值，利用密度函数及图象的性质，并结合相关的选项加以分析与判断.

而方差为σ2=100，即这次测试的成绩的方差为100，故选项B错误；

结合正态密度曲线关于直线x=μ=90对称，可知分数在120分以上的人数与分数在60分以下的人数大致相同，故选项C错误，选项D正确.

故选择答案：AD.

点评：处理此类涉及概率与统计的综合应用问题时，结合题设中对应的概念或关系式，借助相关性质特征、公式应用等加以合理数据分析，从中挖掘对应的参数信息与数据信息，进而加以分析应用与决策判断.本题通过多选题的形式，利用数据分析，巧妙将正态分布中的众多概念、公式等基本知识交汇与融合在一起，考查数学基础知识.

4 基于创新定义进行数据分析

通过对概率与统计中的创新定义（概念创新、公式创新等）的应用，挖掘相关的数据信息，进而加以合理数据分析与应用.

分析：根据题设条件中散度的创新定义，结合离散型随机变量X，Y的概率分布所对应的数据信息，利用创新定义所对应的公式构建关系式，结合对数运算，二次函数、对数函数的图象与性质等来综合应用，进而确定X，Y的散度D（X||Y）的取值范围问题.

故填答案：[0，+∞）.

点评：处理此类创新定义的数据应用问题，关键在于正确把握创新定义的内涵与实质，综合获取的数据信息，利用创新定义中的公式、性质特征等来合理构建对应的关系式，并结合概率与统计知识来分析与处理，得以合理综合应用与决策处理.

在概率与统计的教学中，应合理引导学生根据已知条件进行数据分析，

增强用数据表达现实问题的意识和根据数据认识事物的思维品质，全面提升数据分析能力，不断提高数学应用能力，增强数学思维品质，培养数学核心素养.