巧用二次函数，突破数列最值问题

顾宁 王永生

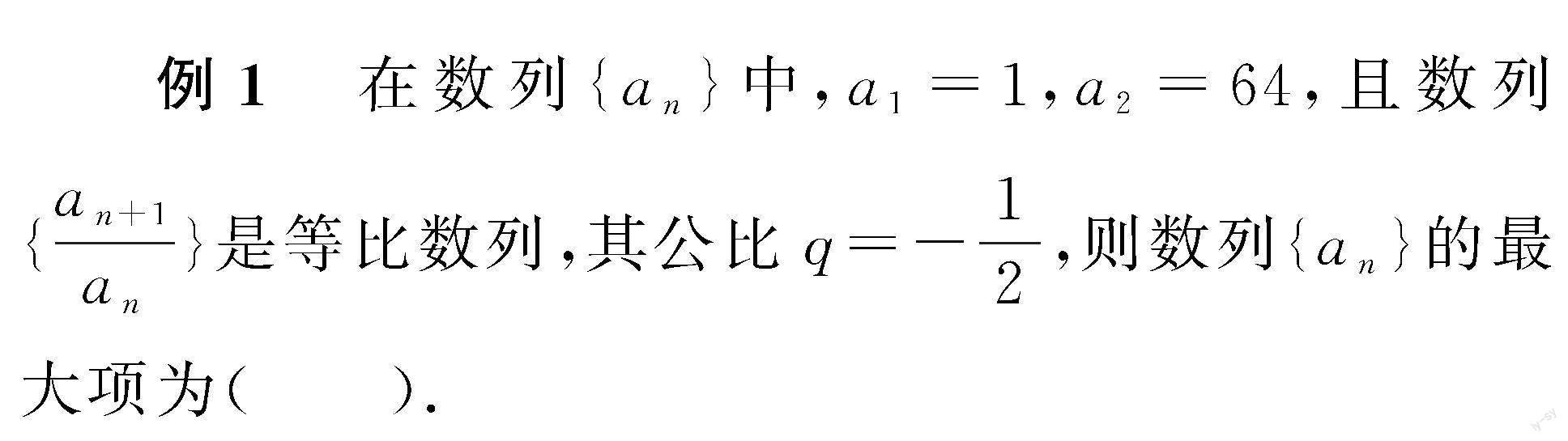
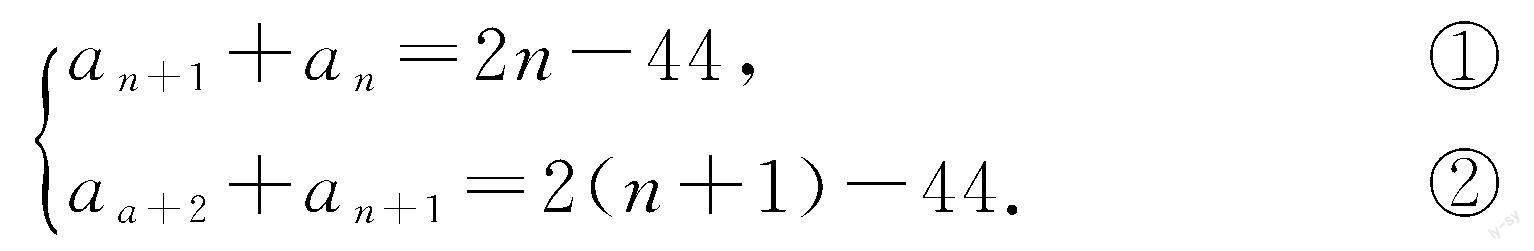
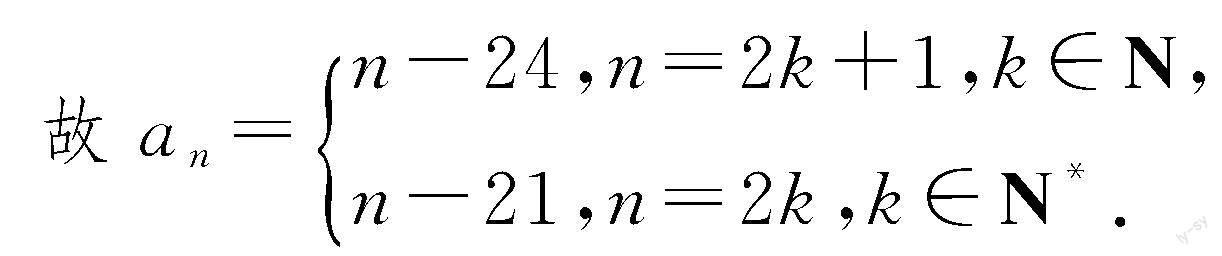
摘要：数列是高中数学的重点与难点.数列最值问题是各类测试的常考点.求数列最值的方法因题而异，其中二次函数法是求解数列最值问题的常用方法.为提高数列最值问题求解效率，应提高二次函数应用意识，借助二次函数性质、图象特点，顺利寻找到解题切入点.

关键词：二次函数；数列；最值问题；突破

众所周知，数列是一种特殊的函数.这一特点为使用函数知识解决数列问题提供了可行的依据.在高中阶段，数列问题的解决中或多或少应用到了函数知识，尤其在解决数列最值问题时，注重二次函数知识的应用，可获得事半功倍的解题效果.

1 求数列项的最值

A.a7

B.a8

C.a6或a9

D.a10

由于n∈N*，结合二次函数性质，可知f（n）的最大值在对称轴或其左右取得.

最大项为a6或a9.

故选答案：C.

点评：该题难点在于通过累乘求出数列{an}的通项公式［1］.同时，要能从二次函数视角切入，通过分类讨论得出最值.

2 求代数式的最值

例2 已知Sn为等差数列{an}的前n项和，其中a1>0，公差d<0，若对任意的n∈N*，总存在k∈N*，使得S2k-1=（2k-1）Sn，则k-9n的最小值为（）.

A.-74

B.-64

C.-53

D.-43

分析：结合“S2k-1=（2k-1）Sn”以及等差数列性质构建ak和Sn的关系式，由已知条件通过推理得出的d和a1的关系，利用等量代换将要求解的代数式的值转化为关于n的二次函数，进而求解.

故选答案：C.

点评：该题难度较大，解题的关键在于从已知条件入手，通過严谨的推理得出相关参数之间的内在逻辑关系，将代数式的最值问题转化为求二次函数的最值问题［2］.

3 求参数的最值

分析：运用数列的第n项和前n项和Sn之间的关系，并结合奇数项和偶数项推理出数列{an}的通项公式以及Sn的表达式，构建n和m的关系，借助关于n的二次函数求出m的最大值.

解：由anan+1=2Sn，得an+1an+2=2Sn+1，an≠0.两式相减得an+1an+2-anan+1=2Sn+1-2Sn，即an+1＼5（an+2-an）=2an+1.又an+1≠0，所以an+2-an=2.

当n为奇数时，由a1=1，得a3=3，a5=5，……，a2k-1=2k-1.

当n为偶数时，由a1=1，anan+1=2Sn，得a2=2，a4=4，……，a2k=2k.

当n∈N*时，f（n）单调递增，则f（n）的最小值为f（1）=2，故m的最大值为2.

4 求前n项和Sn的最值

例4 已知数列{an}中，a1=-23，an+1+an=2n-44（n∈N*）.

（1）求an；

（2）若数列{an}的前n项和为Sn，求Sn的最小值.

分析：运用已知条件分别推理出数列{an}奇数项、偶数项的通项公式，求出数列的前n项和Sn，结合二次函数不难求出Sn的最小值［3］.

解：（1）根据题意，有

②-①，得an+2-an=2.

又由a2+a1=2-44，a1=-23，得a2=-19；同理可得a3=-21，a4=-17.

所以a1，a3，a5，……，是以a1=-23为首项，公差为2的等差数列；a2，a4，a6，……，是以a2=-19为首项，公差为2的等差数列.

（2）由（1）可知，当n为偶数时，

当n为奇数时，

综上，当n为奇数时，Sn取得最小值-243；当n为偶数时，Sn取得最小值-242.

点评：解题时需充分理解题意，正确运用题目给出的已知条件，从数列的奇数项、偶数项入手进行分类讨论，得出对应的an，Sn，然后运用二次函数性质求出最终结果.

综上所述，运用二次函数求解数列最值问题的关键在于灵活运用数列知识进行正确的推理、巧妙的转化，化难为易，通过整理向二次函数靠拢.

参考文献：

[1]周文国.谈数列最值问题的求解策略[J].高中数理化，2023（7）：52-55.

[2]武笎.谈数列问题中求最值项的常用策略[J].数学之友，2023（1）：54-56.

[3]孟金梅.等差数列前n项和最值问题的解法分析[J].中学数学，2022（1）：93-94.