基于GPU的宽带信号时延差与相位差估计方法*
2023-11-25毛飞龙焦义文高泽夫王育欣
毛飞龙,焦义文,马 宏,李 超,高泽夫,王育欣
(航天工程大学 电子与光学工程系,北京 101416)
0 引 言
随着航天技术与深空探测技术的迅猛发展,各国对空间的探测向着更深更远的范围拓展,探测距离将从目前月球探测的40万km拓展到火星探测的4亿km和木星探测的10亿km[1]。这将导致严重的传输损耗[2],同时也对深空探测航天器和地面设备提出了两点要求:一是远距离通信能力;二是高速率传输能力[3]。由于深空探测航天器的等效全向发射功率(Effective Isotropic Radiated Power,EIRP)有限,为了实现对低信噪比信号的高质量接收,就必须增大地面站的天线口径。根据NASA的任务参数计算可知,火星探测任务中,传输1 Mb/s的信号需要直径80 m的天线。而目前NASA深空网(Deep Space Network,DSN)的直径70 m天线已接近工程极限,伺服机动十分困难,灵活性较差。同时,天线的口径越大,其信号的波束越窄,越难以捕获探测器的下行信号。因此,单天线的性能提升已经到了缓慢发展接近停滞的状态,通过多天线合成的方法获得更高的深空通信增益是值得大力发展的方法[4]。
随着高速率通信系统的发展,信号的带宽、传输速率在近年来也有了大幅度提升。信号带宽可达几十MHz甚至几百MHz,这将为地面接收设备带来巨大挑战。宽带信号多天线合成系统是一个数据密集、计算密集、逻辑复杂的计算系统,使用单纯的中央处理器(Central Processing Unit,CPU)计算已不能满足运算要求,需要选用新的计算架构来提高系统实时处理的性能。近些年来,图形处理单元(Graphics Processing Unit,GPU)在计算领域得到了充分应用,已发展成为一种高度并行化、多线程、多核的通用计算设备,具有杰出的计算能力和极高的存储器带宽,并被越来越多地应用于图形处理之外的计算领域。基于GPU的信号处理技术成为众多领域的热点,如射电天文、雷达、无线通信、人工智能等。因此,基于GPU的宽带信号多天线合成具有一定的工程研究意义。多天线信号合成技术的本质就是在消除不同天线信号间的时延差和相位差后进行相干相加,因此天线间时延差和相位差的估计、时延差与相位差的补偿为多天线合成中的两项关键技术。本文旨在现有宽带信号时延差与相位差估计方法的基础上,设计基于GPU的宽带信号时延差与相位差估计方法,通过算法的并行化映射寻求一种精度高且实时性好的估计方法。
1 宽带信号估计方法分析
1.1 多天线信号合成方法
多天线信号合成的概念最早是由美国喷气推进实验室于1965年提出的[25]。该技术通过将不同天线接收到同一信源的信号进行合成,从而提高接收信号的信噪比(Signal-to-Noise Ratio,SNR)。图1为多天线信号合成原理示意图。以双天线为例,两天线接收到来自同一信源的信号,通过AD采集为数字信号,然而由于各天线信号传播路径的不同,导致信号间存在各种各样的差异,这些差异将损失信号间的相干性。此时两天线信号存在时延差与相位差。将其中值较高的天线当作参考天线,另一天线为待补偿天线,对其进行时延差与相位差估计并补偿,将两天线的时延与相位对齐。之后对两天线信号相加,就得到了信号幅度翻倍、信噪比提升的合成信号。多天线信号合成技术的本质就是在消除不同天线信号间的时延差和相位差后进行相干相加。由于各天线间的噪声是随机非相关的,理论上使用N个天线合成信号的信噪比是单天线接收信号的N倍。

图1 多天线信号合成原理示意
多天线信号合成技术经过几十年的发展,逐渐形成了5种合成方案[6]:全频谱合成、基带合成(Baseband Combining,BC)、符号流合成(Symbol-Stream Combining,SSC)、载波组阵合成(Carrier Arraying,CA)、复符号合成(Complex-Symbol Combining,CSC)[7]。除全频谱合成方法之外,其余四种方法都属于基于载波跟踪技术的合成方法,都需要阵元载波锁定后合成,不适用于当前大规模的多天线信号合成。本文在考虑分析了各种方法的利弊后,选用全频谱合成方法对宽带信号进行合成。
1.2 现有宽带信号时延差与相位差估计方法
宽带信号合成的关键是对宽带信号间的残余时延和相位进行高精度估计和补偿,目前可以分为时域合成方法和频域合成方法。
1.2.1 时域合成方法
NASA深空网在其全频谱处理阵(Full Spectrum Processing Array,FSPA)设备中,使用了一种基于上下边带的残余时延和相位差联合估计方法,原理如图2所示。该方法首先通过提取信号滤波器(中心频率可调带通滤波器)提取各天线信号的上边带和下边带,然后利用相位估计算法分别估计待校准天线与参考天线上下边带的相位差,最终两相位点构成的直线的斜率即为残余时延,截距即为载波相位差。

图2 基于上下边带的残余时延和相位估计方法的原理
在图2中,L1和L2表示两天线信号经过提取信号滤波器(中心频率可调带通滤波器)得到的下边带,其中心频率为fL;U1和U2表示两天线信号的上边带,其中心频率为fU;相位差φL和φU为相位差估计算法估计得到的下边带间和上边带间的相位差。则两相位点构成直线的斜率即为残余时延,截距即为载波处的残余相位。设残余时延为Δτ,载波处的残余相位为Δφc,则有
(1)
(2)
该方法的优势在于运算量小,而且将时延估计问题转化为相位估计问题,在低信噪比条件下,各边带可以采用高性能相位估计算法来提高估计精度。然而,该方法存在两个问题,下面进行详细分析。
1)相位卷绕问题
由于相位估计算法只能提取初相差,当上下边带频率差较大或者残余时延较大时出现相位卷绕问题。而该方法只取了上下边带两个相位差值进行估计,在没有时延差与相位差先验知识的情况下无法正确地进行解卷绕处理,进而导致残余时延和残余相位与其真实值差距较大。
本文研究宽带信号的合成方法,以典型的Ka频段信号为例,其信号带宽可达500 MHz,若采用基于上下边带的残余时延和相位差联合估计方法,在接收信号的上下边带分别进行互相关,当上下边带频率差较大或者残余时延较大时,得到上下边带的相位结果为其卷绕的值。因此,为了得到正确的残余时延与残余相位,就要保证不发生相位卷绕(φU-φL<2π),此时
(3)
当Δf为250 MHz时,Δτ为4×10-9s,即为4 ns,而Ka频段的宽带信号通常残余时延为几十ns甚至几百ns,因此引入可消除相位卷绕现象的残余时延与残余相位估计方法是宽带信号合成中的重点之一。
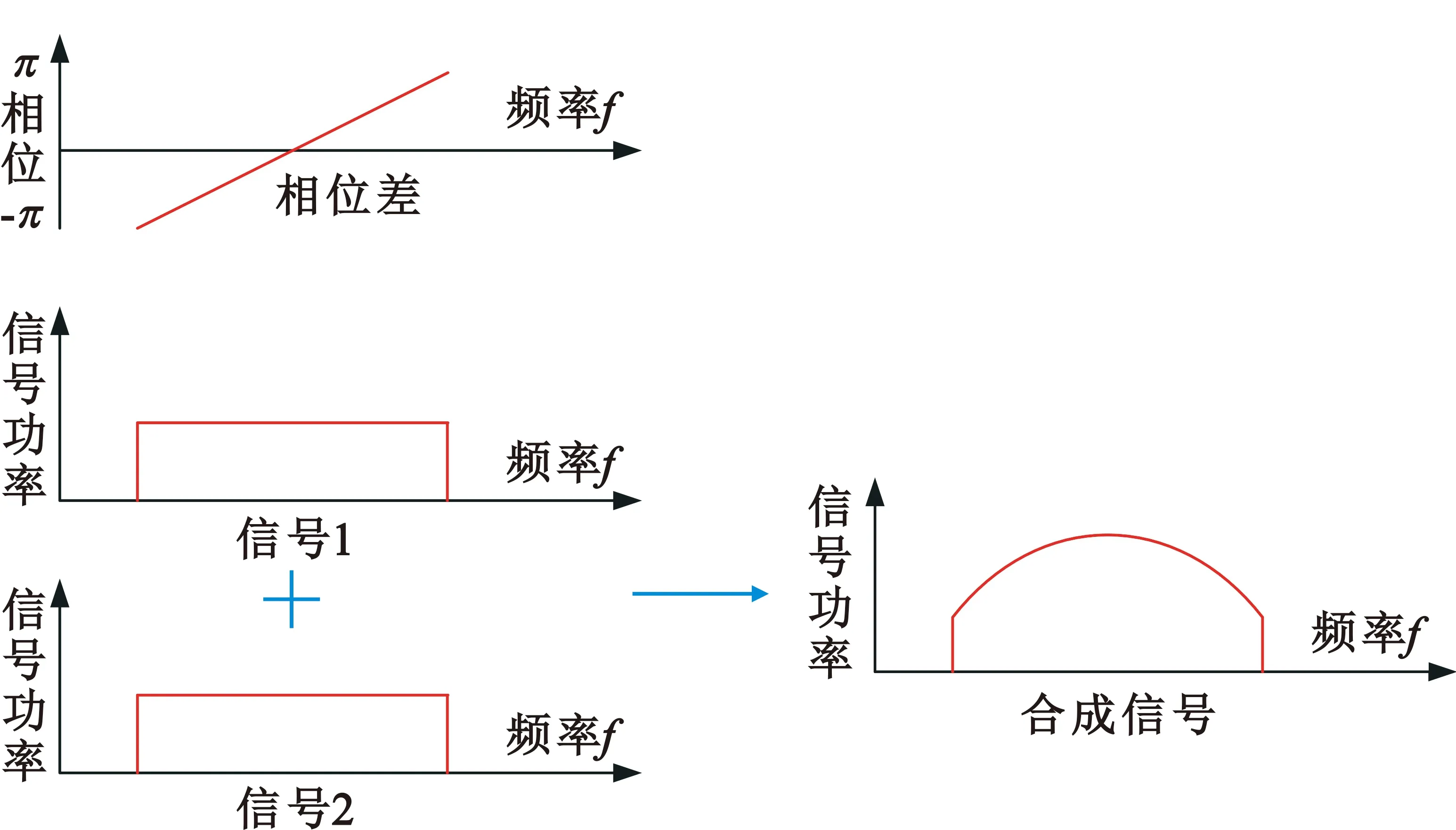
2)频带内相位滑动问题
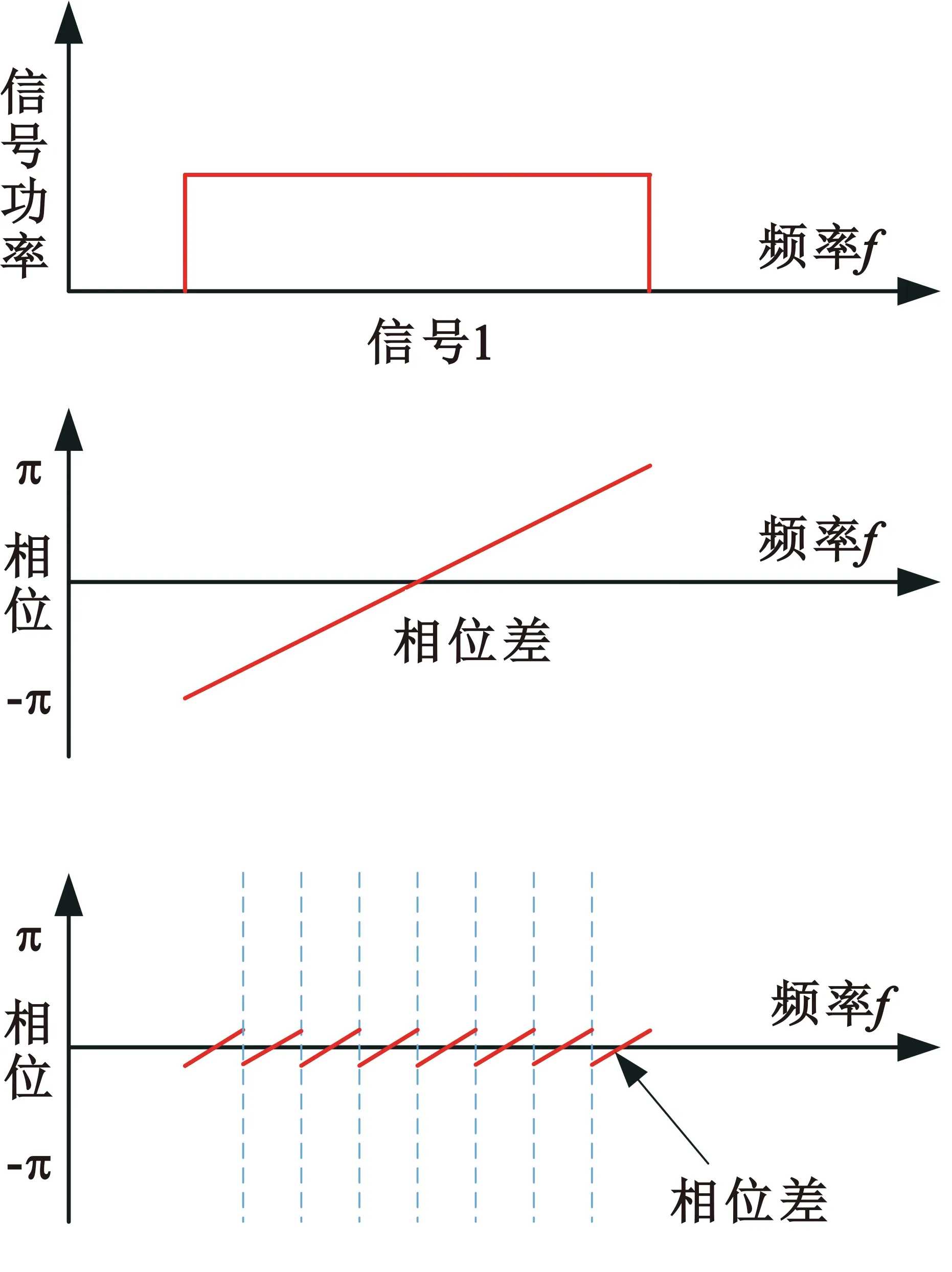
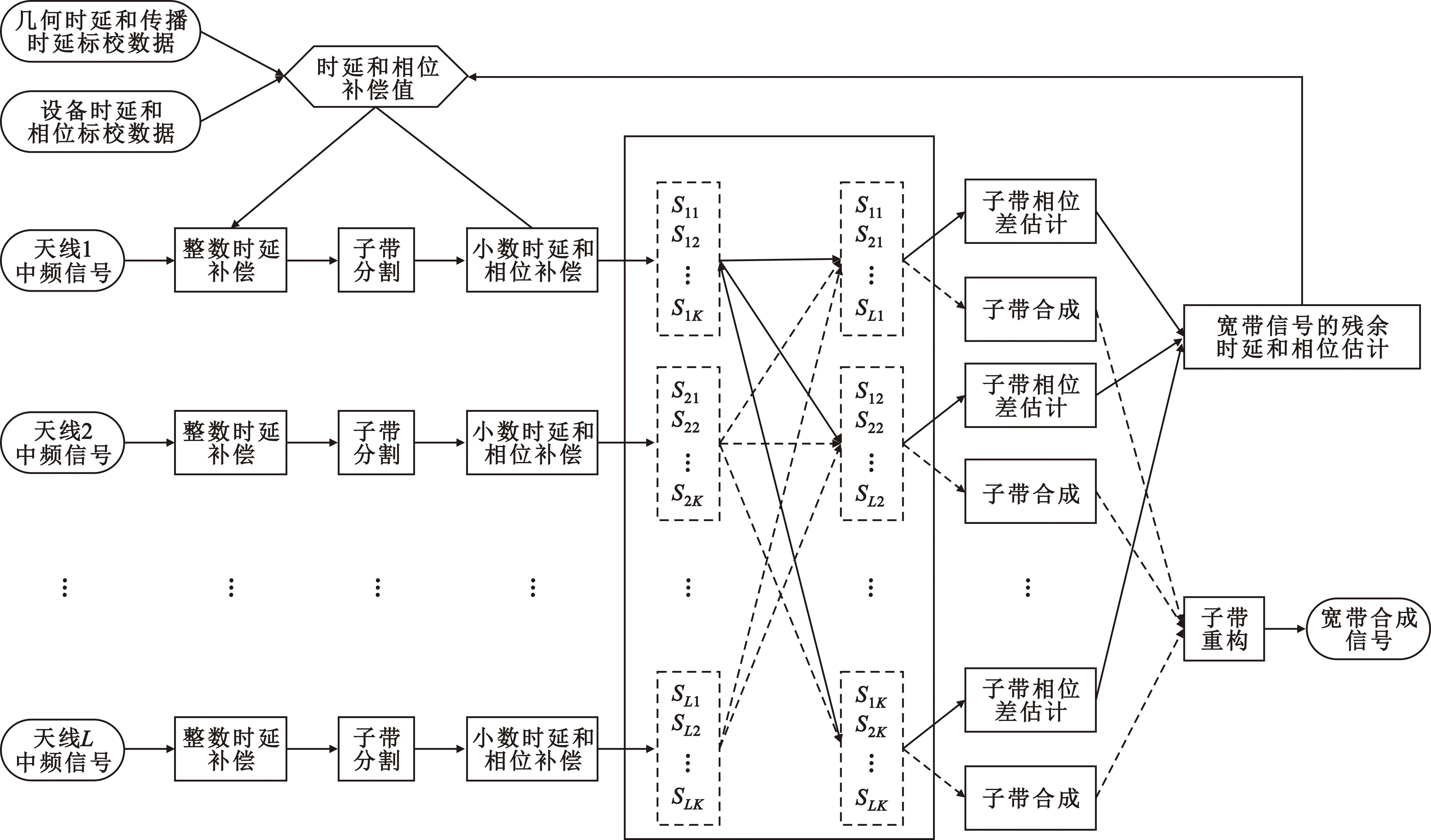
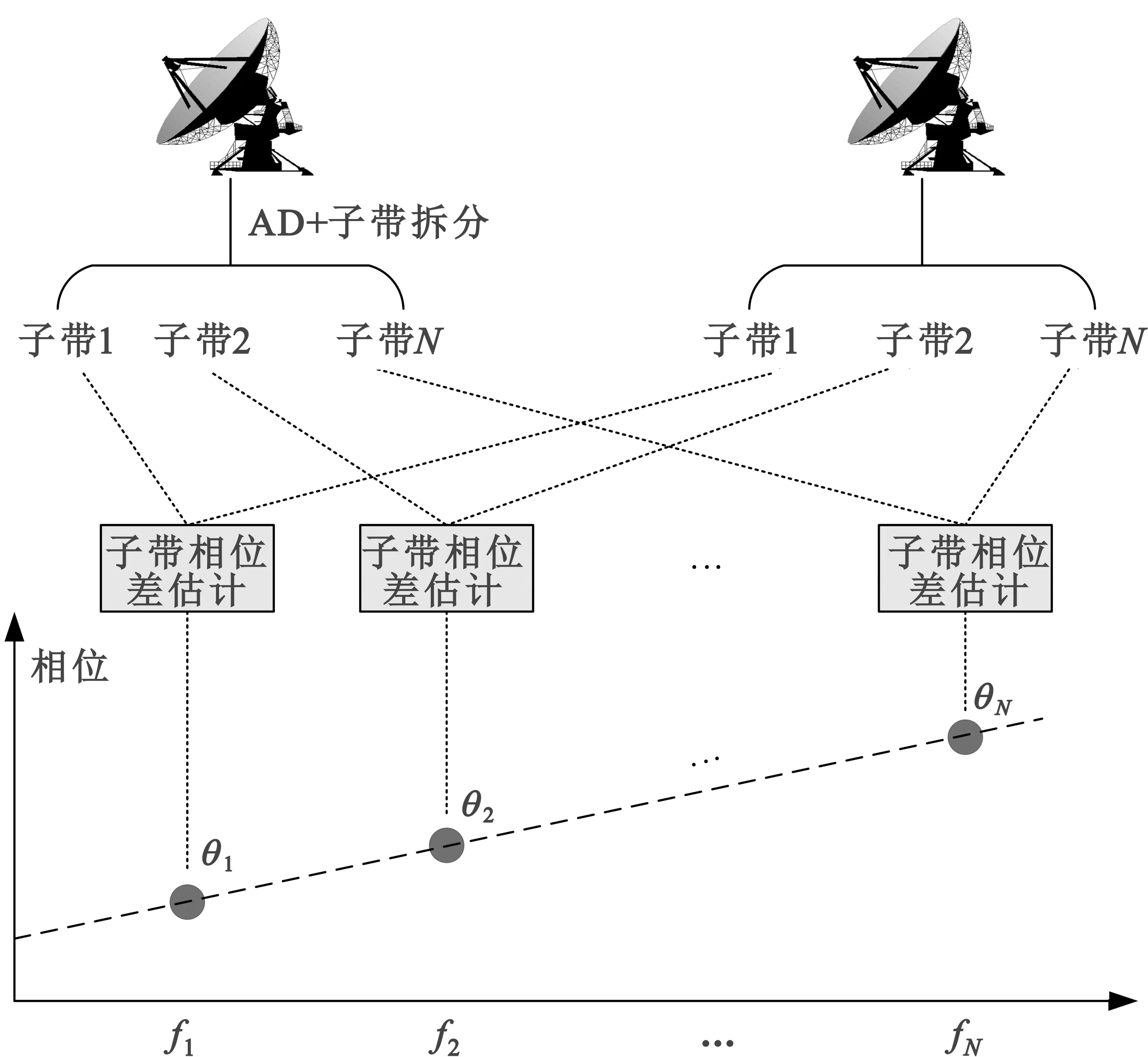
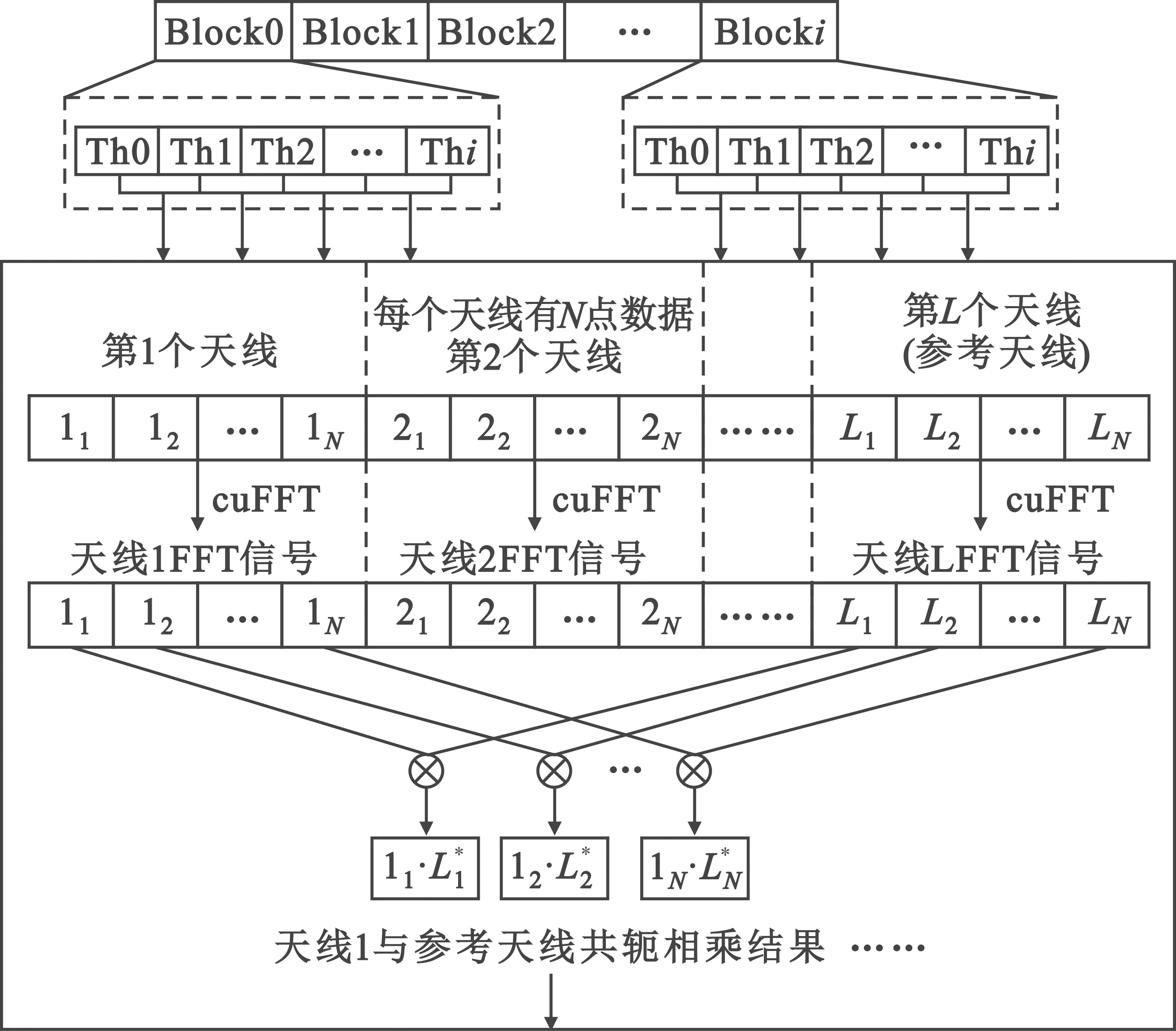
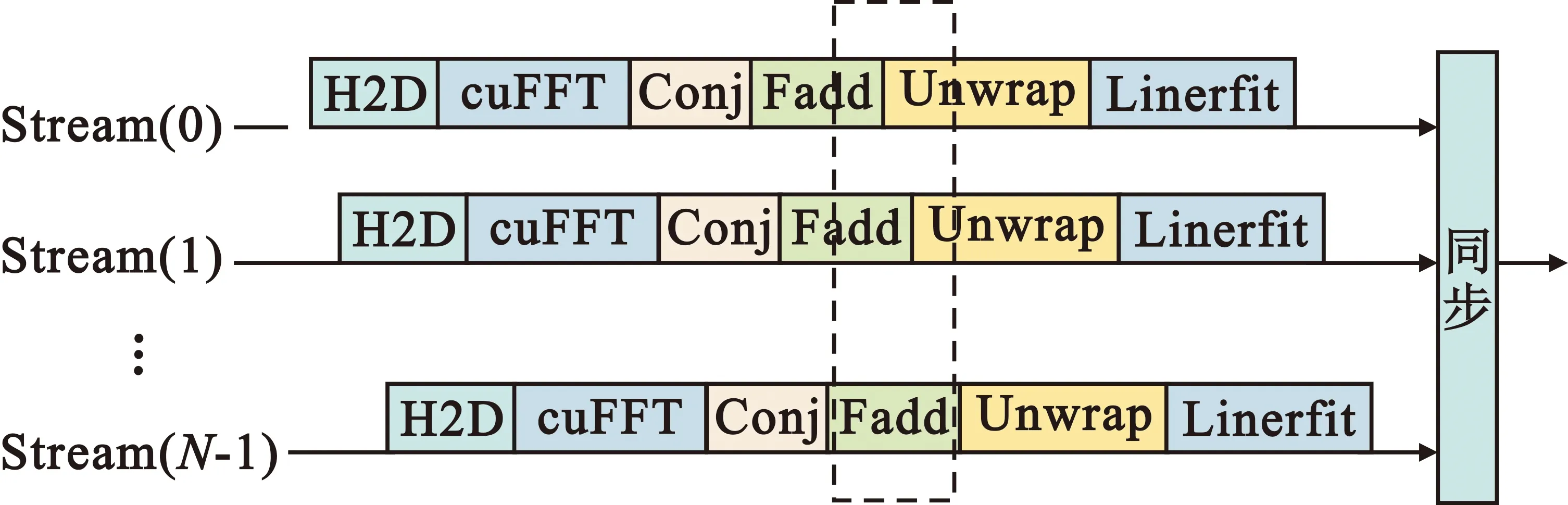
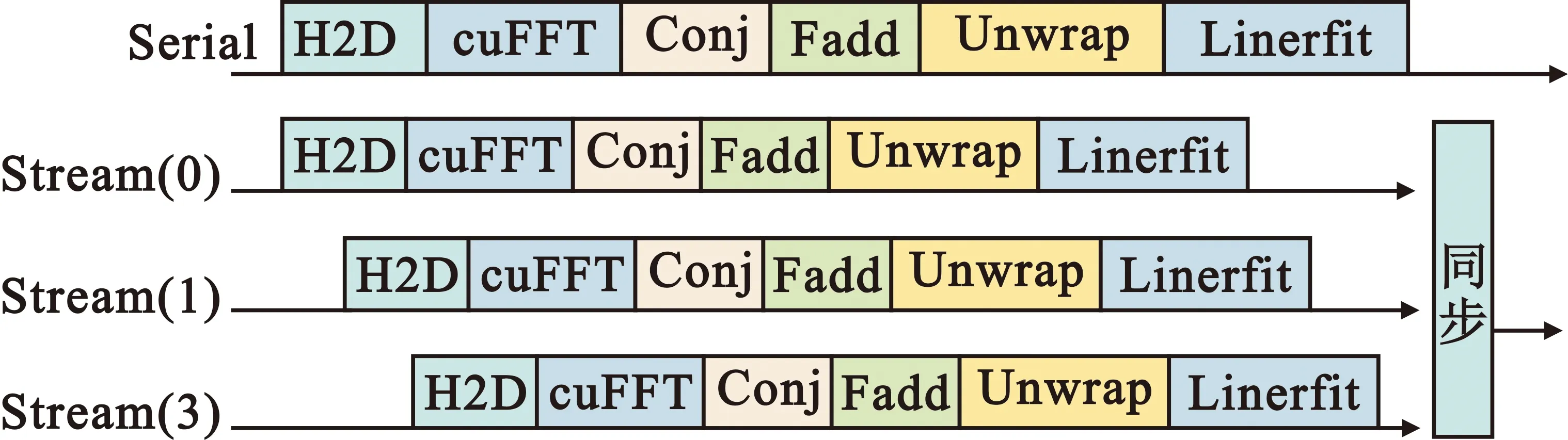
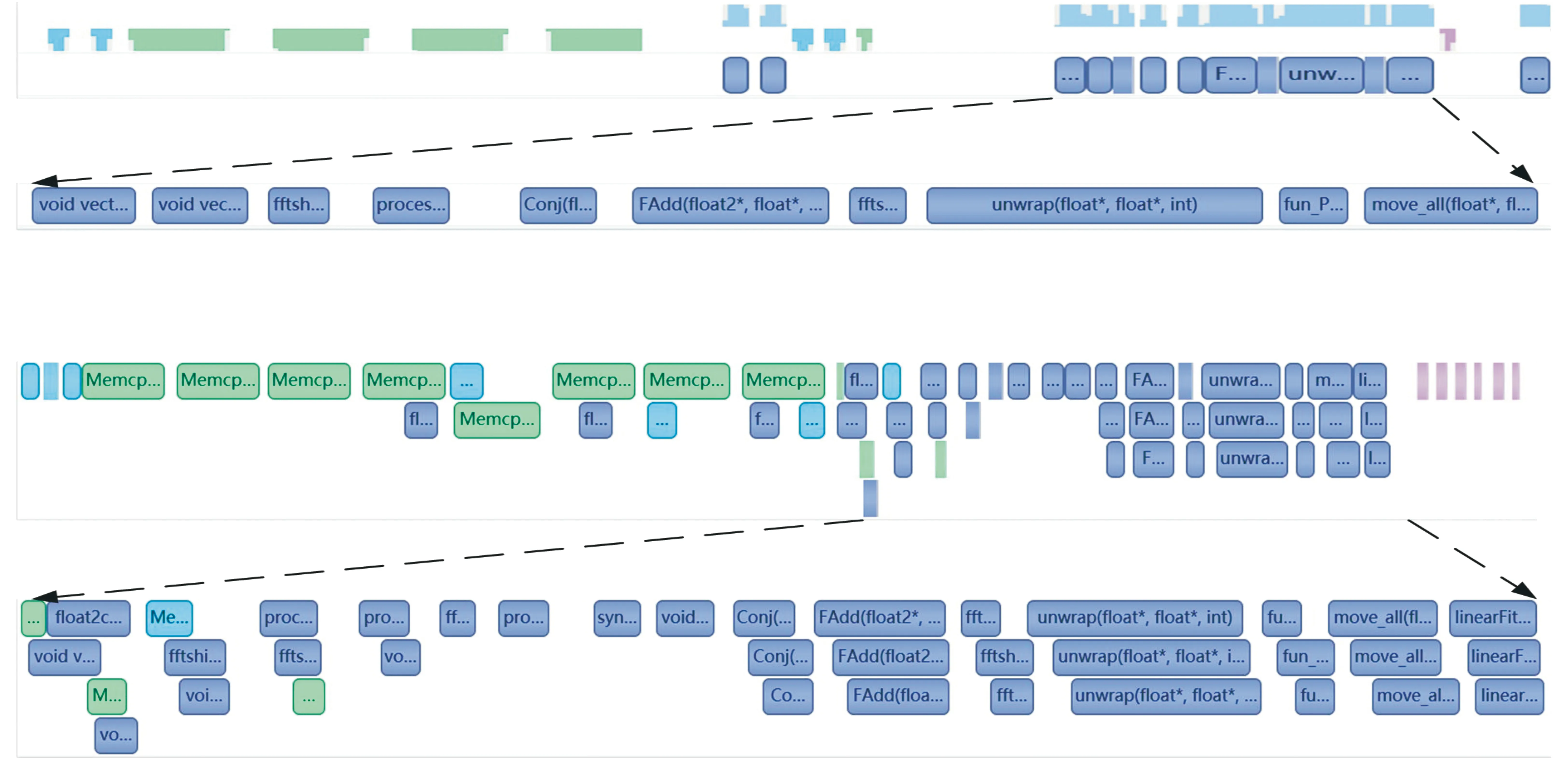
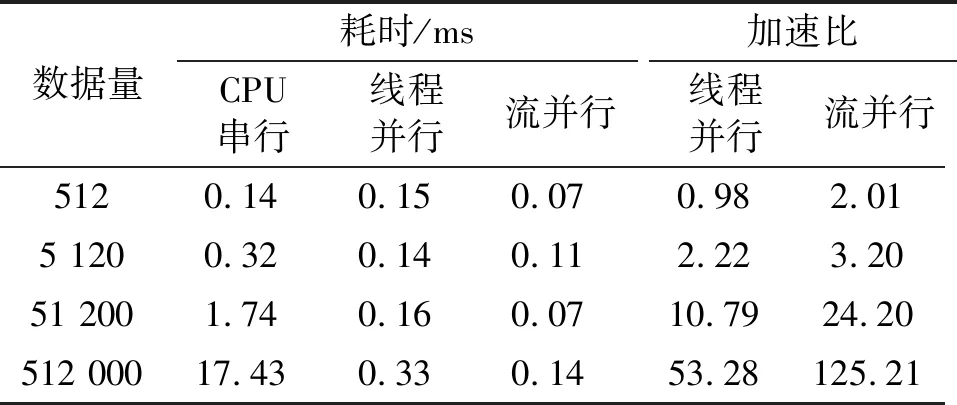
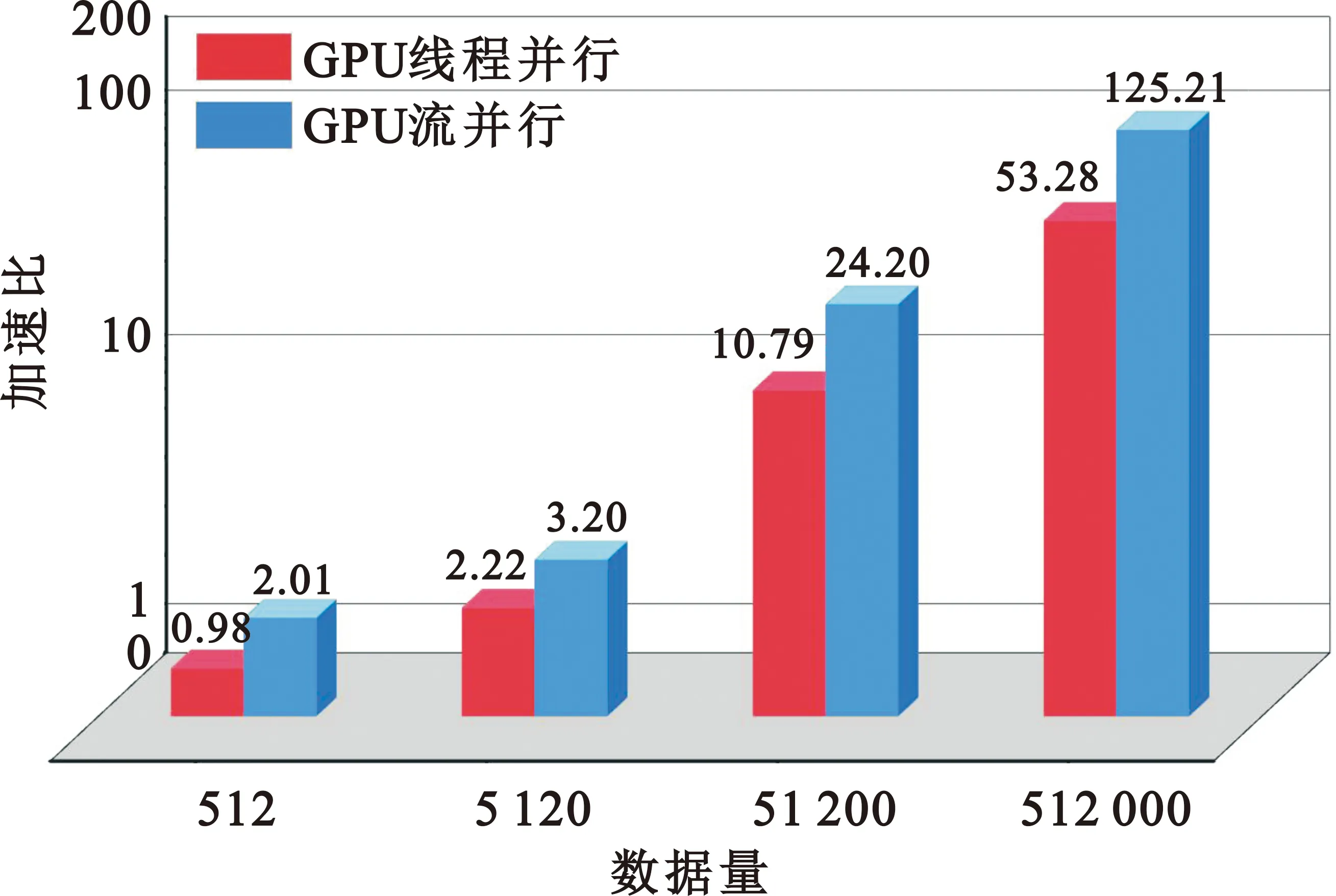
整数时延补偿都采用整数时钟移位的补偿方法,其最高精度为时钟的周期Ts,整数时延补偿之后必然存在Δτ Δφ=2π·fU·Δτ-2π·fL·Δτ=2π·Δf·Δτ。 (4) 式中:Δφ为相位滑动;Δf为频率高处与频率低处的差值。相位滑动现象将影响合成信号的质量,当Δφ=0时,信号的带宽较窄,可近似看作同一频率,各处的相位补偿值相同,信号合成的性能较好,如图3所示;当Δφ=π时,相位补偿为真实值的负值,将导致合成信号出现反向相消的现象,如图4所示。 图3 无相位滑动现象示意图 图4 有相位滑动现象示意图 为了抑制反向相消现象,需保证Δφ<<π,即2π·Δf·Δτ<<π,若Δf为250 MHz,需满足Δτ<<2 ns,同样地,需要满足采样时钟Ts<<2 ns,即采样率需远大于500 MHz。考虑到信号带宽为500 MHz时,根据奈奎斯特采样定理,只需采样率大于1 000 MHz即可。而远大于500 MHz的采样率将带来采样效率极大地浪费,同时也增加了系统实时处理的难度。因此,引入可消除相位滑动现象的残余时延与残余相位估计方法也是宽带信号合成中的重点之一。 由上述分析可知,时域合成方法都存在补偿精度受采样率限制的问题。即使假设时延估计误差为零,补偿后的小数时延(也称作分数时钟时延,最大为半个采样时钟周期)也将导致频带内的相位滑动,从而恶化合成性能。尤其当带宽较大时,上述方法不再适用。因此,引入更合理的小数时延补偿方法是宽带信号合成的重点和难点问题之一。 1.2.2 频域合成方法 频域合成方法的处理流程为首先利用分析滤波器组对宽带信号进行信道化,得到低采样速率的子带信号,再利用相位差估计技术得到不同天线子带间的相位差,进而估计宽带信号间的残余时延和相位并对其进行补偿,然后对各天线子带进行合成,最终利用综合滤波器组对各天线合成后的子带进行重构,得到原始采样率的宽带合成信号。在对残余时延进行补偿时,首先采用数字延迟线进行整数时延补偿,残余的小数时延以及相位的补偿则在频域进行,通过对各个子带进行线性相位偏移来实现。相比较时域合成方法,频域合成方法具有如下优势:一是通过对子带构成的相频曲线进行解卷绕,可以有效解决时延差引起的2π模糊问题;二是通过将各子带中心频率独立进行相位对齐,可将由小数时延引起的整带内相位滑动限制在子带范围内,大大减小了小数时延引起的合成损失。 由上述分析可知,频域合成方法可以有效解决时域合成方法存在的问题,已得到广泛关注和研究,是目前宽带信号全频谱合成的最佳实现方法。可以预见,该方法将是未来大规模宽带天线组阵信号合成的主流方法。 由1.2节分析可知,现有的基于上下边带的残余时延和相位差联合估计方法在处理本文中带宽500 MHz的信号时存在两方面问题,分别是相位卷绕问题和频带内相位滑动问题。对相位卷绕问题分析可知,其主要出现在上下边带频率差较大或者残余时延较大时,而信号的残余时延差Δτ无法改变,只能通过减小频率差Δf来改进。对频带内相位滑动问题分析可知,Δφ<<π时,该现象可消除。而Δφ=2π·Δf·Δτ,同样地,由于Δτ无法改变,只能通过减小频率差Δf来减小相位滑动问题带来的影响。综合上述因素,减小频率差Δf是一种改进思路,结合软件无线电中信道化的思想,将各天线的信号拆分为多个独立的子带,之后对不同天线对应的子带信号进行处理。下面进行详细分析: 将宽带信号拆分为K个子带,对相应的子带进行相位差估计,得到K个子带对应的相位差信息。此时,只要保证相位差出现卷绕现象是由于某一子带的相位差值在[-π,π]之外引起的,而并非相邻两个相位差的差值大于2π引起的,换句话说,只要保证相邻两个相位差不存在卷绕现象就可正确进行解卷绕。在各子带中,频率间隔在数值上为fs/K,要使相邻两个相位差不存在卷绕现象,即 (5) 式中:τd为子带内的最大时延。式(5)可化简为 (6) 由式(3)可知,K需满足 K>2fs·τd。 (7) 因此,当时延差τd的精度确定时,子带的最小数量即确定。 对于频带内相位滑动问题,将宽带信号拆为子带信号进行处理,可将相位滑动限制在子带范围内,如图5所示。可以看出,虽然没有彻底消除相位滑动问题,但相位滑动被限制在了很低的范围内,可大幅度降低相位滑动问题对合成性能的影响,使合成信号的功率谱保持在可接收的范围内,如图6所示。 图5 相位滑动现象被限制在子带内示意 图6 减弱相位滑动前后合成信号功率谱示意 宽带信号合成需考虑相位卷绕问题和频带内相位滑动问题,根据上述分析可知,将宽带信号拆为子带进行处理可有效地降低这两种问题带来的影响。同时,宽带信号合成方案必须考虑相频特性差异造成的相位非相干性以及采样率高带来的数据吞吐率大的问题。因此,本文选用宽带信号频域合成方法,如图7所示。 图7 宽带信号频域全频谱合成方法 基本思路为首先根据频率范围对宽带信号进行子带拆分,得到低采样速率的子带信号。利用相位差估计技术得到不同天线子带信号间的相位差,进而估计并补偿宽带信号间的残余时延和相位,然后对各天线子带进行合成。最终通过对各天线合成后的子带进行重构,得到原始采样率的宽带合成信号。 宽带信号时延差与相位差估计示意图如图8所示。以双天线为例,天线信号经AD采集与子带拆分之后,每个天线信号得到了频率范围不同的K个子带。对两个天线对应频率的子带信号进行相位差估计,得到K个子带的相位差结果。由于宽带信号的相位信息φ(ω)是频率ω的线性函数,且满足 图8 宽带信号时延差与相位差估计示意 φ(ω)=ω·Δτk+θk。 (8) 则宽带信号的残余延迟差Δτk多项式为一次项参数,即斜率,残余相位差θk为零次项参数,即截距。因此,在估计得到两个天线子带间的相位差信息后,通过线性最小二乘拟合就可以得到两天线宽带信号的残余时延与残余相位。由于子带相位差估计方法最后需要进行反正切运算,因此,当残余时延对应整周期内的角度大于2π时,就会出现相位卷绕现象。因此,需要在拟合之前进行解卷绕得到正确的相位值。 图9为基于GPU的宽带信号时延差与相位差估计流程,具体步骤如下: Step1 参考天线与待补偿天线首先经过FFT均匀信道化器将宽带信号拆为多个子带信号。 Step2 待补偿天线的子带信号均与参考天线对应的子带信号进行共轭相乘运算,完成互相关。 Step3 将多段互相关的结果进行累加平均并求反正切,得到对应子带相位差的估计值。 Step4 待补偿天线各子带的相位值进行解卷绕运算得到正确的相位值。 Step5 对待补偿天线所有子带的相位差结果进行最小二乘线性拟合,得到宽带信号的时延差与相位差。 其中Step 1~3即为子带相位差估计算法中典型的Simple算法。 由1.3节可知,子带相位差估计算法中Simple算法主要包括FFT、共轭相乘、累加平均三个模块,下面对各模块的GPU实现方法进行研究。 在CPU平台下,N点FFT的运算量为N/2×lbN次的复数乘法和N×lbN次的复数加法,N表示做傅里叶变换的点数。对于如此大量的高速并行数据,在CPU平台中无法做到实时处理。但是由于FFT计算具有高度并行性这一显著特点,本文考虑将快速傅里叶变换部分放在GPU中进行并行加速处理,利用CUDA中自带的CUFFT库,可实现大量高速数据的实时FFT计算。调用CUFFT函数库内的cufftPlanD函数对数据进行快速傅里叶变换。在GPU上进行快速傅里叶变换需要完成以下几步工作: Step1 使用 malloc()函数为输入的数据分配主机端(CPU)内存,并存储输入数据。 Step2 使用 cudaMalloc()函数为输入数据分配设备端(GPU)显存。 Step3 使用 cudaMemcpy()函数将主机(CPU)内存数据传输到设备端(GPU)显存。 Step4 创建一个plan,调用 cufftPlanD函数创建快速傅里叶变换。 Step5 执行plan,使用 cufftExecC2C()函数完成plan的计算任务。 Step6 用cudaMemcpy()将GPU端显存数据传输到主机内存。 上述工作执行完成以后如果这个plan不再需要,则调用cufftDestroy()函数销毁该plan及分配给它的计算资源。以上各步的具体流程和所调用的CUDA函数如图10所示。在CUFFT库中,有3种不同的库函数:cufftExecC2C(复数到复数)、cufftExecC2R(复数到实数)、cufftExecR2C(实数到复数),它们的计算耗时由于本身运算量的差异而有所不同。因此,为最大限度地缩短运算时间,必须针对本提相过程的实际情况,选择最合适的库函数类型。在本系统输入信号的FFT计算中,由于输入是复信号,而输出是复数信号,因此最宜采用cufftExecC2C类型的FFT。 图11是GPU中FFT与共轭相乘模块的实现框图。调用cufft库进行FFT、多个线程同时进行共轭相乘运算,代码如下: 图11 FFT与共轭相乘GPU实现框图 cufftPlan1d(&plan,NFFT,CUFFT_C2C,nBatch); cufftExecC2C(plan,d_signal,d_signal_FFT,CUFFT_FORWARD); cufftDestroy(plan); Conj<< __global__ void Conj(float2 *src,float2 *send,float2 *dst,int length) { int tid = threadIdx.x + blockIdx.x * blockDim.x; if(tid >= length) return; dst[tid].x =(src[tid].x * send[tid].x + src[tid].y * send[tid].y); dst[tid].y =(src[tid].y * send[tid].x - src[tid].x * send[tid].y);} 图12为累加平均并求相位核函数实现框图。将共轭相乘后数据传输至累加平均并求相位核函数中进行能量累积和提相等处理。将每个天线的N个数据等分成x段进行相加平均,每段M/x点,累加平均后使用atan 2函数求出M/x个复数的相角,所得相角即为子带间的相位差。 图12 累加平均并求相位GPU实现框图 本文设计的累加平均并求相位核函数部分的CUDA代码如下所示: FAdd<< __global__ void FAdd(float2 *src,float *dst,float *dst2,int jft,int length) { int tid = threadIdx.x + blockIdx.x * blockDim.x; if(tid >= length) return; int curpos; double sum_x = 0.0; double sum_y = 0.0; for(int i = 0;i { curpos = tid + i * length; sum_x = sum_x +((double)src[curpos].x); sum_y = sum_y +((double)src[curpos].y);} sum_x = sum_x / jft; sum_y = sum_y / jft; dst[tid]= atan2(sum_y,sum_x); dst2[tid]= 10 * log10(sum_x * sum_x + sum_y * sum_y);} 如图9所示,基于GPU的宽带信号时延差与相位差估计流程主要包括在GPU平台上进行FFT、子带相位差估计、解卷绕、拟合等。子带相位差估计具体包括共轭相乘、累加平均等运算,FFT过程可用CUDA的库函数CUFFT进行计算,而CUFFT库提供的二维FFT计算模型为本文的多路FFT高效并行实现提供了可能。 流(stream)是CUDA环境中的一个并行概念,在GPU中可使用流来处理并发操作[8]。流本质上是一个操作队列,该队列可由主机上不同的线程发出并以异步方式在GPU上按顺序执行。不同的流可以并发执行,多个流并发执行不同路数据的FFT、子带相位差估计、解卷绕、拟合等运算,可大大提高运算的并行性。基于GPU的宽带信号时延差与相位差估计,各路数据完全独立,每一路数据的处理包含FFT、共轭相乘、累加平均、解卷绕、拟合等多个操作,因此,可进一步利用异步流并发技术对估计方法进行优化。 设天线数为N,若将每一路天线数据的处理过程用一个CUDA流来处理,则基于CUDA流式架构的相位差估计算法实现框图如图13所示。由图中虚线框所示部分可知,在该算法中,同一时刻最多有N个Kernel在同时执行。 图13 基于CUDA流式架构的相位差估计算法实现框图 图14为N=3时流式架构相位差估计算法流程。从图中可知,基于线程的并行方法中,数据传输和核函数顺序执行,即一次操作完全完成后才进行下一项操作,在某次操作执行期间其他所有操作都处于等待状态。而在流式结构并发算法中,数据传输和核函数的执行被拆分为多个并行的操作序列,随着CUDA流的并发启动,数据传输过程被核函数执行过程较好地隐藏。另外,从图14的算法结构对比结果可看出,3路并行流式结构并行算法在执行时,同一时刻驻留在GPU上的核函数最多可达3个,其执行效率明显高于线程并行算法。 图14 基于CUDA流式架构的4天线相位差估计算法实现框图 首先利用线程并行的方式对时延差与相位差估计方法中的共轭相乘、累加平均、解卷绕等模块的实现算法进行了相应的改进和优化,实现了多个线程同时处理多个数据的运算,提高了每个核函数本身的运算效率。之后利用异步流并发的方式对估计方法进一步优化,每路信号采用独立的流进行运算,从结构层面有效提高了数据的并行处理效率。 本文采用Simple算法对宽带信号进行合成,利用相位干涉仪中的4个天线进行实测数据信号合成。系统由4个阵元构成,阵元摆放形式如图15所示。系统硬件平台选用NVIDIA Tesla V100显卡,接收信号频段采用S频段,利用相位校正(Phase CALibration,PCAL)信号进行性能分析,PCAL信号的频率特性具有梳状频谱特性和线性相位特性。本系统的核心设计指标如表1所示。 表1 仿真实验参数 图15 相位干涉仪布阵示意 首先验证GPU线程并行与GPU流并行估计方法的正确性,设置天线4为参考天线,天线1与天线4的时延差为2个采样点、相位差为-π/2。利用CPU串行Simple算法、GPU线程并行Simple算法与GPU流并行Simple算法估计天线1与参考天线的时延差与相位差。每次估计出时延差与相位差后对天线1信号进行修正,按式(9)更新时延和相位补偿值: (9) 式中:delaynow和phasenow为本次迭代计算出的时延差与相位差;delayi-1和phasei-1为上一次迭代的时延和相位补偿值;delayi和phasei为本次更新后的时延补偿值。步长因子为0.5,记录迭代30次的时延和相位补偿值。 图16为CPU串行Simple算法、GPU线程并行Simple算法与GPU流并行Simple算法的时延和相位补偿值随迭代次数变化的曲线。20次迭代后,三种算法的时延和相位补偿值都收敛于真值,都可实现高精度时延和相位估计,验证了GPU线程并行与GPU流并行估计方法的正确性。 利用本文中的并行Simple算法与传统串行Simple算法在不同单天线信噪比的条件下分别进行合成,进行蒙特卡洛仿真并得出合成损失与合成效率的平均值,得到不同信噪比条件下两种方法的合成损失与合成效率。图17给出了两种方法在不同单天线信噪比条件下合成损失与合成效率的仿真结果。 (a)合成损失 从图17可以看出,本文中的并行Simple算法与传统串行Simple算法的合成损失与合成效率曲线重合,两者的合成性能一致,与分析得出的结论一致。同时,两种算法随着单天线信噪比的升高,合成损失降低,合成效率升高。仿真结果表明,本文中的并行Simple算法与传统串行Simple算法在信噪比高于-15 dB的条件下有较好的合成性能。 为了详细分析核函数运行过程,利用NVIDIA Nsight Systems对流式架构Simple算法进行分析,结果如图18和图19所示。 图18 CUDA流式架构Simple算法时序图 图19 CUDA流式架构Sumple算法时序图 图18中上方为未采用异步流并发方式优化的Simple算法时序图,可以看到同一时刻最多只有一个核函数驻留,不同天线的相同运算模块顺序运行。图18中下方为采用异步流并发方式优化的Simple算法时序图。由于Simple算法将其中1个天线设置为参考天线,因此,在天线数为4的情况下只需进行3路信号流并发即可。从图18中可以看到同一时刻最多有3个核函数驻留,不同天线的相同运算模块分别在3个不同流上执行。 图19中上方为未采用异步流并发方式优化的Sumple算法时序图,可以看到同一时刻最多只有一个核函数驻留,不同天线的相同运算模块顺序运行。图19中下方为采用异步流并发方式优化的Sumple算法时序图。由于Sumple算法将所有天线的加权值设置为参考天线,每路天线信号都要与虚拟的参考天线进行时延差与相位差估计,因此,在天线数为4的情况下需要进行4路信号的流并发。从图19中可以看到同一时刻最多有4个核函数驻留,不同天线的相同运算模块分别在4个不同流上执行。从时序图中可明显地看出异步流并发适合于时延差与相位差估计方法的优化加速。 下面对GPU线程并行与GPU流并行估计方法相比CPU串行方法的加速比进行测试,分别对30次迭代中CPU串行、GPU线程并行与GPU流并行估计方法的耗时进行记录。共测试4组,每组的区别只有迭代的数据量,分别为512,5 120,51 200,512 000。表2加速比测试结果。 表2 加速比测试结果 图20为GPU线程并行与GPU流并行估计方法相比CPU串行方法的加速比测试结果图,可以看出,当数据量为512时,GPU线程并行方法相比CPU串行方法的加速比为0.98,表明此时的GPU线程并行方法的平均耗时大于CPU串行方法的平均耗时。因为当数据量较小时,每个核函数调用的线程数较少,不能充分地发挥GPU多线程的优势,因此没有加速效果。GPU流并行方法相比CPU串行方法的加速比为2.01,虽然数据量较小时不能发挥GPU多线程的优势,但是流并行方法在结构上对运算顺序做了优化可以利用多流并发的方式同时对多路信号进行运算,因此加速效果明显。随着数据量的升高,GPU线程并行与GPU流并行估计方法相比CPU串行方法的加速比也升高,表明GPU线程并行与GPU流并行估计方法适合大规模数据的实时处理。从表2可以看出,CPU串行、GPU线程并行、GPU流并行估计方法在数据量为512 000的估计耗时约为17.43 ms,0.33 ms与0.14 ms。本文中系统的采样率为56 000 000,处理512 000数据量耗时若小于10 ms即可实现实时估计。因此,CPU串行估计方法无法实现实时估计,本文中的GPU线程并行、GPU流并行估计方法可实现实时估计。此外,本文中的数据为仿真数据,提前读入GPU,而实际系统中,受限于系统吞吐率与GPU并行性能的限制,实际系统的加速比不能无限增大。 图20 加速比测试结果 针对大规模多天线信号合成系统的天线数量越来越多,接收信号的带宽越来越大,单独使用CPU已不能满足运算需求这一问题,本文研究了宽带信号时延差与相位差估计方法,分析了算法并行的可行性并设计了基于GPU的宽带信号时延差与相位差估计方法,通过仿真对比实验验证了本文提出的并行算法的优越性。 本文的并行算法可以运用到未来的大规模宽带信号多天线信号合成系统中,实现高速、准确、实时的信号合成,有力支持未来的一系列深空探测任务。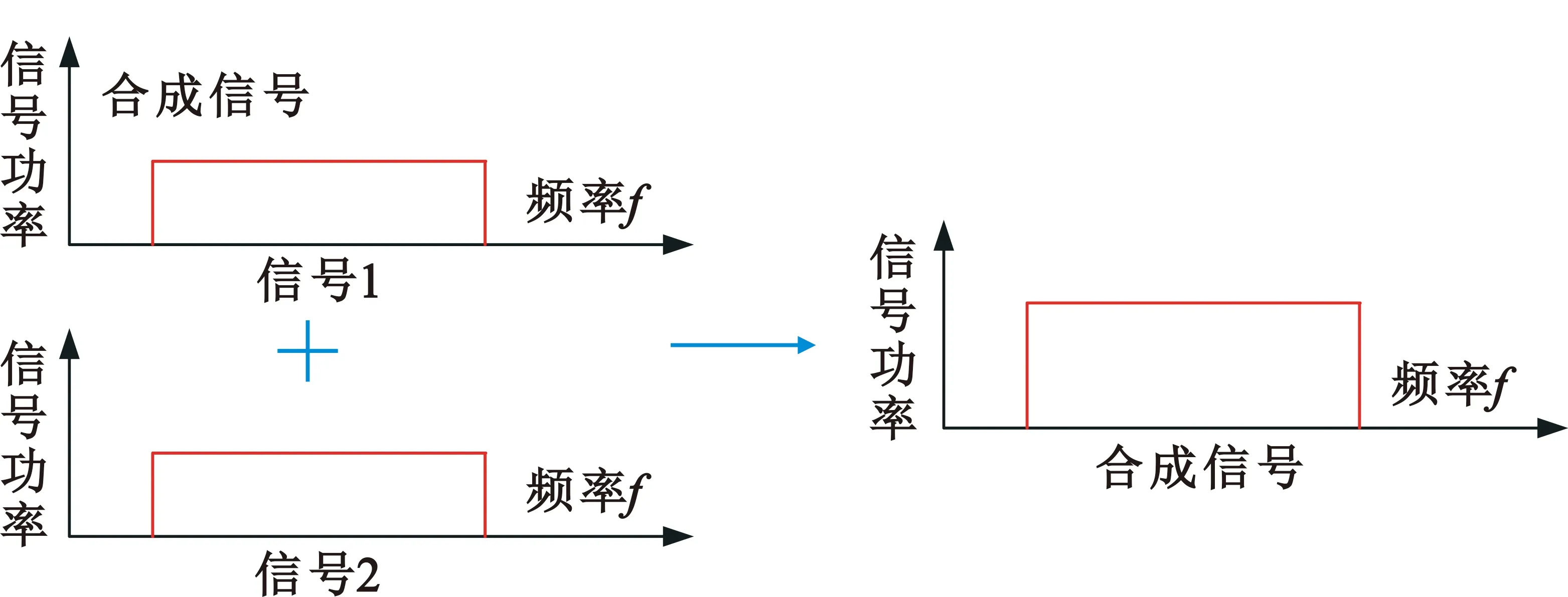
1.3 本文采用的宽带信号时延差与相位差估计方法

2 GPU并行优化
2.1 线程并行优化

2.2 异步流并发优化
2.3 小结
3 仿真验证
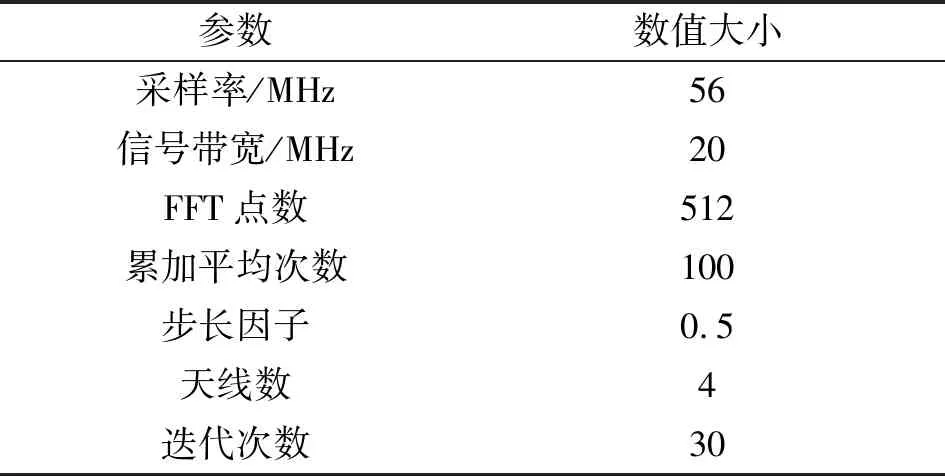
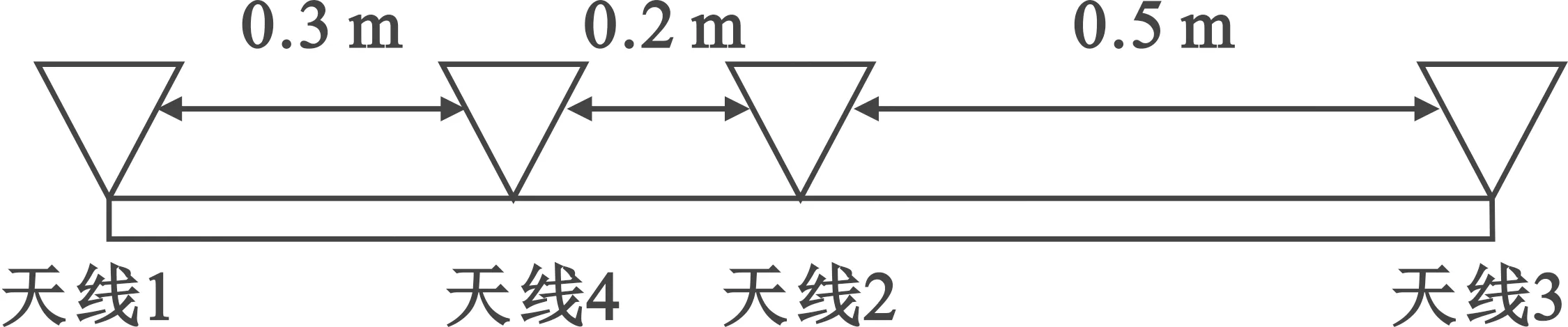
3.1 正确性验证
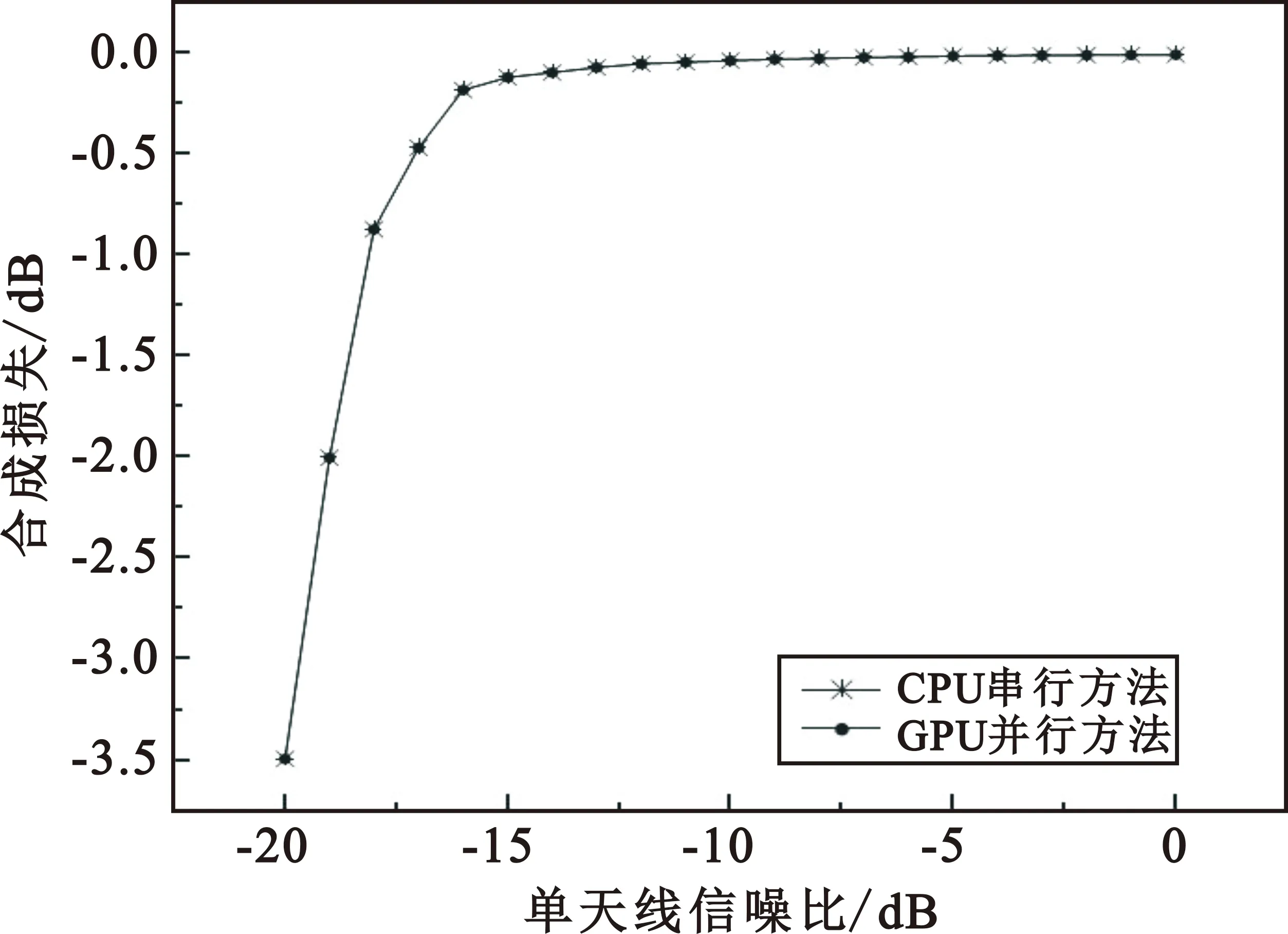
3.2 加速效果验证

3 结 论
