一种基于深度学习的高轨卫星CEI信号频率估计算法*

2023-11-25高泽夫杨文革焦义文毛飞龙王育欣李雪健张书雅

电讯技术 2023年11期

高泽夫,杨文革,焦义文,毛飞龙,王育欣,李雪健,张书雅,李超,2,滕飞

(1.航天工程大学 a.电子与光学工程系;b.航天指挥学院,北京 101416;2.电子信息系统复杂电磁环境效应国家重点实验室,河南洛阳 471003)

0 引言

随着空间探测技术的发展,地球静止轨道(Geostationary Orbit,GEO)因其独特的高轨和静地特性,目前已成为通信、气象、侦察、跟踪以及科学研究等的重要轨道类型[1]。我国针对高轨卫星的传统测量手段是基于航天测控网的统一测控系统,通过测量卫星的距离、速度及角度信息实现测量和定位。目前这一手段的测控能力和测量精度均已无法满足日益增长的实际需求,因此,研究针对高轨卫星的近实时、高精度和高可靠性的测量定位技术是十分必要的。

传统的RAE测量技术(R为距离,A为方位角,E为俯仰角)无论单站还是多站,均为主动式测量,需要目标卫星合作转发测距信号。相比之下,基于被动式干涉测量的卫星轨道测量技术具有显著优势[2]。干涉测量技术主要利用不同测站接收同一高轨卫星的信号相位差,来实现目标卫星至测站间时延差的测量,从而完成对于高轨卫星的精确定轨。

相位干涉测量技术是一种基于飞行器下行信号的被动测角跟踪方法,目前主要有甚长基线干涉测量(Very Long Baseline Interferometry,VLBI)和连线干涉测量(Connected Element Interferometry,CEI) 这两类技术。国外利用干涉测量技术在高轨卫星轨道测定领域开展了一系列研究[3-4]。近年来,国内基于VLBI技术,开展了GEO卫星对地观测、在轨航天器信号接收等的研究[5-6];基于CEI技术,在GEO卫星定轨、月球探测等领域也开展了一系列研究[7]。

与VLBI相比,CEI的主要优点是:相位延迟测量比较简单,可实现对相位差的快速定轨,几乎可以做到实时测角[8];设备简单,费用低,维护和管理方便,非常适用于对同步轨道及其以内地球卫星的现有测控手段进行增强和补充[9]。综上所述,CEI测量体制相比于其他高轨卫星测量技术拥有较为明显的优势,可对高轨卫星提供较强的横向约束,与传统测控技术相结合,可大幅提高我国对于高轨卫星的测量精度,有效提升相应的空间应用能力。

CEI测量实时性要求较高,结合航天测控信号的实际处理特点[10],CEI实现高精度时延测量的关键问题之一是CEI信号的高精度频率估计。该问题可建模为正弦信号的频率估计问题,这一问题是目前通信、雷达、电子对抗等领域的研究热点,国内外许多学者对此进行了大量研究。近年来,直接采用离散傅里叶变换(Discrete Fourier Transform,DFT) 谱估计进行正弦波信号频率估计的方法,由于其计算量小,因而在工程上得到了广泛应用[10-16]。与此同时,基于神经网络和机器学习的信号频率估计算法在近年来也得到了广泛关注和研究[17-23]。基于神经网络的方法侧重于利用神经网络的相关特征来降低算法复杂度,从而提高信号频率估计的速度,但均以估计精度不同程度的下降为代价[18];而基于机器学习的方法则重点利用机器学习方法的优势,将参数估计问题转化为分类问题,同时降低算法的复杂度[20-23],这与本文研究的侧重点即提高频率估计算法的估计精度并不一致。

上述算法均存在一定的局限性:Rife算法[11]在待估计信号的频率偏差较小时估计误差较大;Quinn算法[12]需计算3个谱线插值且无法通过迭代进行性能优化;AM算法[13]需通过多次迭代(极大地增加计算复杂度)以提高频率估计精度。除此之外,这些算法对于本文研究的高轨卫星高精度测量下的CEI信号频率估计这一问题的适配性均达不到要求。

基于上述分析,本文主要针对高轨卫星的CEI信号频率的高精度估计这一难题,构建了CEI中的正弦信号频率估计模型,提出了基于深度学习的CEI信号频率估计算法。需要指出的是,本文所提出的方法实际上不局限于高轨卫星这一应用场景,对于低轨卫星和中轨卫星均有良好的适用性,可以在未来中低轨卫星的CEI测控任务中发挥重要作用。然而,由于在高轨卫星的测量场景中所面临的噪声干扰和其他环境约束更为严苛,使得解决高轨卫星CEI信号中的高精度频率估计难题显得更加迫切,因此本文将重点研究基于深度学习的高轨卫星CEI信号的高精度频率估计方法。仿真结果表明,本文算法较好地实现了基于CEI对于高轨卫星进行测量时的高精度频率估计难题,在未来的空间目标监视,高价值在轨目标长期运行管理等场景中具有一定的应用价值。

1 CEI中的正弦信号频率估计模型

1.1 CEI基本原理

图1所示为CEI基本原理图,CEI测量相关器处理的高轨卫星信号来自几何上分离的两个地面测站。高轨卫星发出的信号波前到达基线两端的时间差近似为:

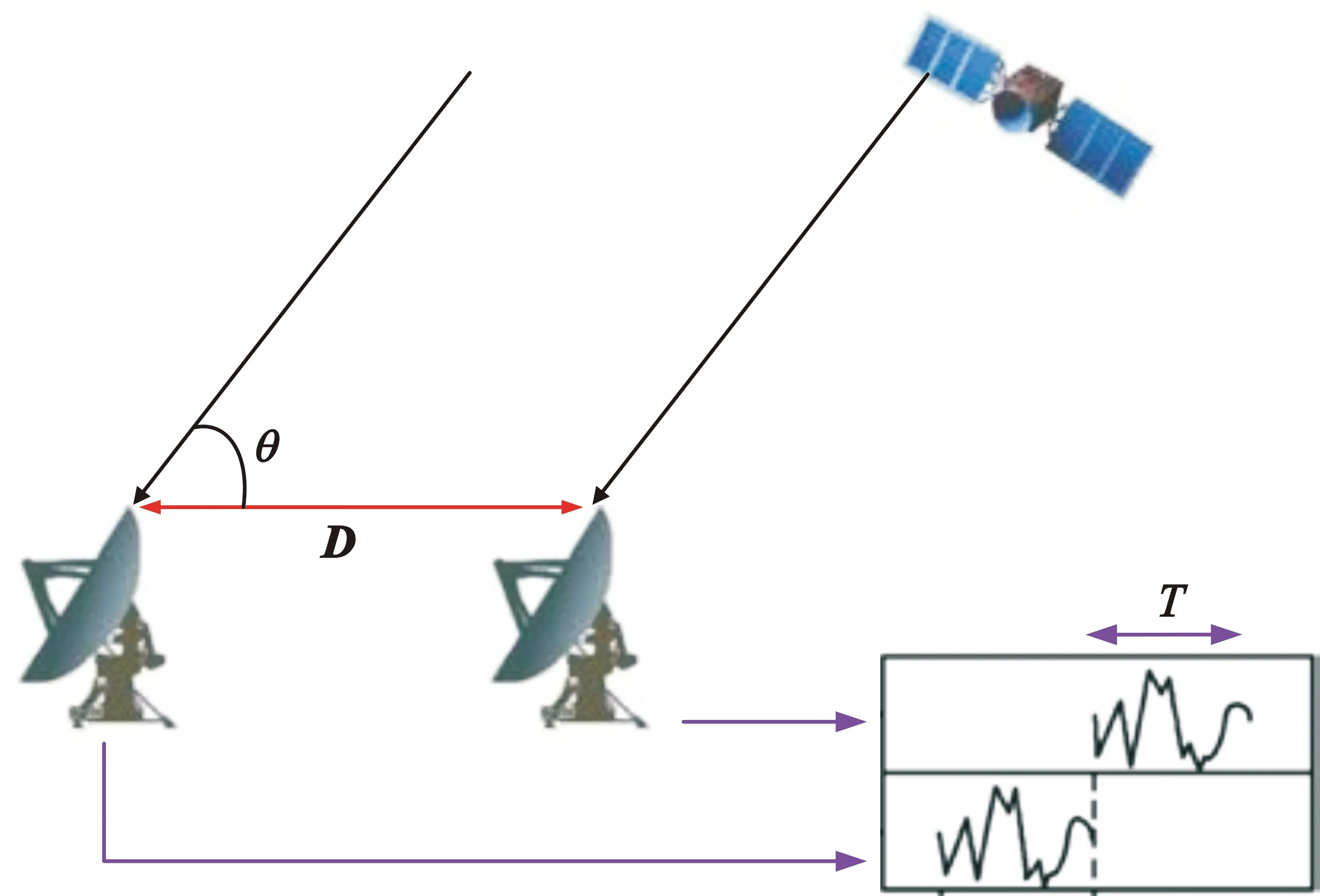
图1 高轨卫星的CEI基本原理

(1)

式中:T为时间差;D为从第一个测站到第二个测站带的基线矢量,S为高轨卫星的方向矢量,S与D的夹角为θ。根据式(1),在基线确定的情况下,由T测量误差导致的θ测角误差表示为

(2)

由式(2)可知,测角误差Δθ与基线D的长度成反比,与T的测量误差ΔT成正比。因此,若要获得高精度角度测量,可以通过提高干涉测量时延的测量精度实现,这也就是CEI高精度测量技术的基本原理。

如图 2 所示,由于卫星轨道误差绝大部分体现在它在有效基线方向上的投影,因此两条CEI正交基线便可以决定高轨卫星的二维角坐标及其变化信息[24]。卫星发出的信号按球面波传播方式建立量测方程[25]。

图2中有两条正交基线,分别由测站1和2以及测站2和3构成。为分析方便,下面将以测站1和2为例建立量测方程:

图2 基于正交基线的CEI精确测量示意

φ+λN=ρ1-ρ2=

|D1(t1)-d(t0)|-|D2(t2)-d(t0)|+

c·Δtclock+Δratm+Δrins+n。

(3)

式中:φ和N分别为相位观测量和整周模糊度;λ为卫星下行波段的信号波长;d和D1,D2分别为高轨卫星和基线1两端测站1和2的位置矢量;Δtclock为两站钟差的互差;Δratm为站间大气传播延迟的残余误差;Δrins为仪器延迟引起的距离误差;n为观测噪声。

1.2 CEI中的正弦信号频率估计模型

CEI信号进行频率估计时,需从两测站接收信号中提取同一侧音s1(t),s2(t),满足如下所示的时域频域关系:

(4)

分别求出s1(t),s2(t)的频率和相位,经过差分处理即可得到差分相位估计和差分时延估计。

将上述过程建模为正弦信号的频率估计问题,如下所示:

xi(n)=Aejφ0ej2πf0nΔt+w(n) 。

(5)

式中:i=1,2,…,k,分别对应测站1,2,…,k;n=0,1,…,N-1,N为采样点数;A为信号幅度;φ0为信号初始相位;f0为信号频率;Δt为采样周期;w(n)是实部和虚部相互独立的,服从N(0,σ2)的复高斯白噪声。

对式(5)做离散傅里叶变换得

(6)

2 基于深度学习的CEI信号频率估计算法

本算法引入了一种新的深度学习框架,实现了对带有噪声干扰的CEI正弦信号的高精度频率估计。灵感来自于文献[14]中的基于学习的方法。该方法生成了一个频率表征模型,如果真实频率的数量已知,则可以使用表征模型来执行较为精确的频率估计。基于此,本文构建了一个新颖的神经网络架构,它将在学习大量CEI数据的基础上产生一个更精确的CEI信号频率估计算法。

2.1 基于深度学习的CEI信号频率估计算法总流程

基于深度学习的CEI信号频率估计算法的总流程如图3所示。

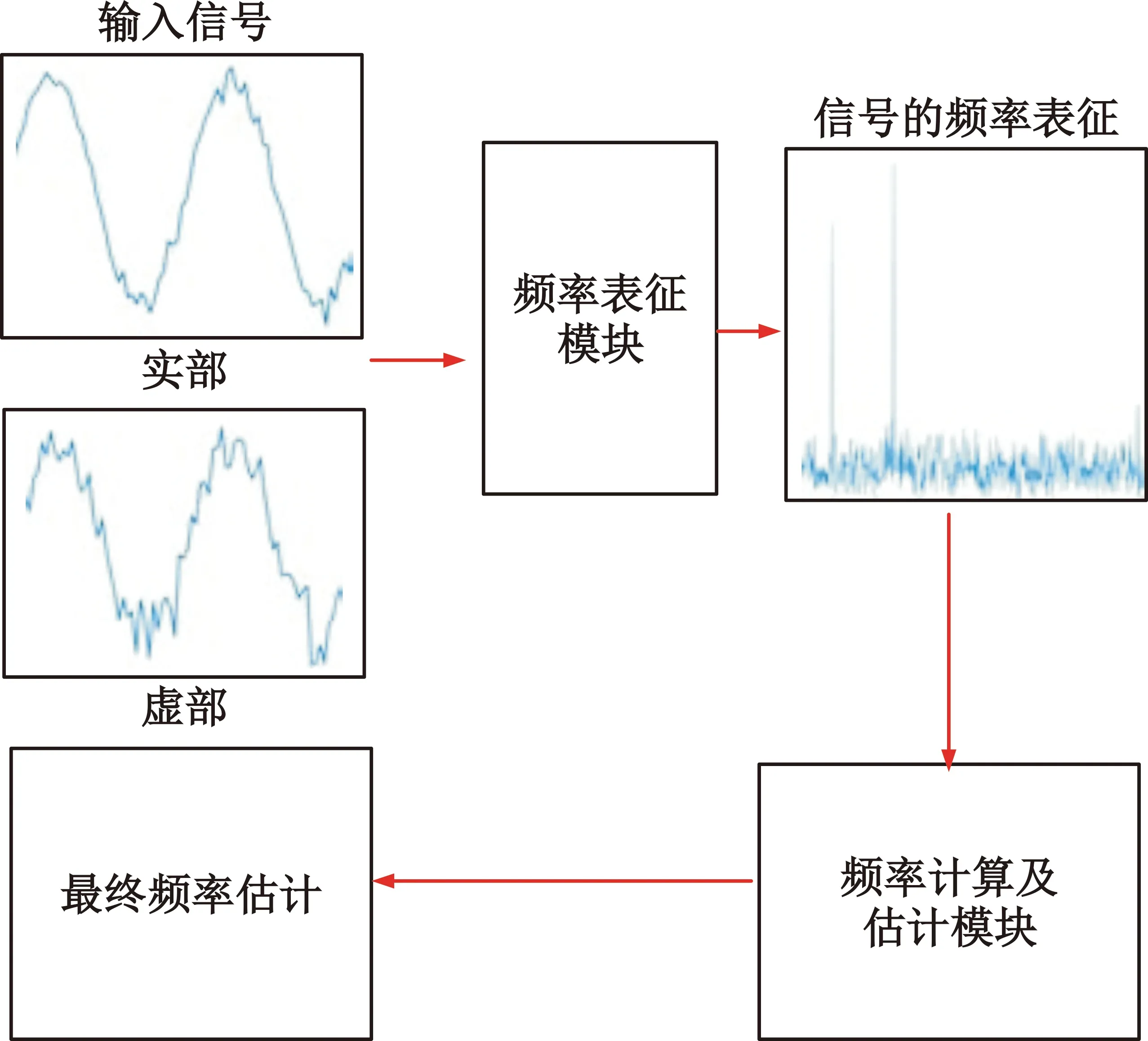
图3 基于深度学习的CEI信号频率估计算法总流程

首先,基于GPU平台,分别对频率表征模块和频率计算及估计模块进行学习和训练,这将产生一个精确的CEI信号频率表征和频率计算及估计模型。接着,将待估计的CEI信号输入到频率表征模块,该模块基于深度前馈神经网络来设计,深度前馈网络具有更多的隐藏层数目,从而具备了更强的特征提取能力;同时,深度前馈网络无需使用相关数据的先验信息,从而可以专注于输出待估计信号的频率表征。然后,将信号的频率表征输入频率计算和估计模块,该模块基于多层卷积神经网络来设计,卷积神经网络能够按其阶层结构对输入信息进行平移不变分类,同时具有较小的计算量和较强的表征学习能力,因而可以有效地计算得出待估计信号的正弦分量数量,最终计算得到输入信号的精确频率估计值。

2.2 频率表征模块

该模块通过前馈深度神经网络来实现CEI信号的频率表征,具体流程如图4所示。首先,线性编码器将输入的待估计CEI数据映射到特征空间,处理完毕后得到一系列信号的特征。然后,这些特征将通过一系列卷积层(Convolutional layer,Conv)、批量归一化(Batch Normalization,BN)和激活函数(Rectified Linear Unit,ReLU)进行处理,同时使用圆形填充保持输入信号的维度,卷积层内含有长度为3的局部滤波器。处理完毕的结果将输入解码器进行进一步处理。最后,解码器应用转置卷积产生FR估计,由此实现了整个频率表征。FR估计的具体表达式将在下文给出。

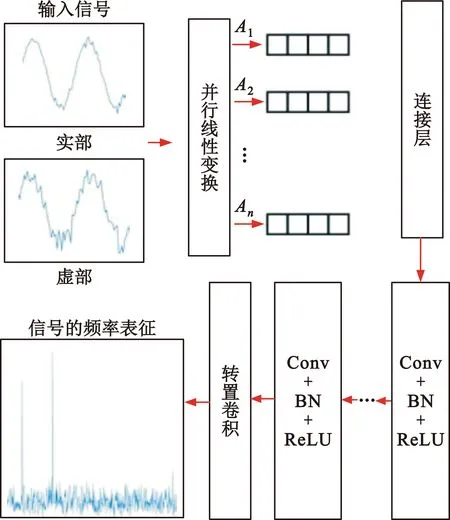
图4 基于深度学习的频率表征模块具体流程

给定一组CEI信号的真实频率f1,f2,…,fm,定义CEI的频率表征FR估计为以每个频率为中心的窄带高斯核函数K:的叠加,如下所示:

(7)

FR是一个平滑的函数,它在真实频率的位置有尖锐的峰值并迅速衰减。

神经网络经过校准,从式(5)的模型给出的N个带有噪声的低分辨率CEI数据中输出一个近似FR,该过程通过最小化训练损失来实现。

该模块使用的线性编码器将学习一个类似傅里叶的转换,这一转换过程将频率信息集中在局部,以便后续神经网络层的卷积滤波器处理。使用多个独立的线性映射,将编码器的输出用一个特征矩阵表示:[G1,G2,…,GC],其中每个Gi(1≤i≤C)是一个固定的M×N维矩阵,C为通道数,它们从输入的CEI信号中提取互补的特征。

下一神经网络层中的过滤器将结合所有通道的信息,同时对特征矩阵的列进行卷积操作,这为卷积层提供了丰富的频率特性,从而提高了频率表征模块的性能。

2.3 频率计算及估计模块

该模块使用多层卷积神经网络来实现CEI信号的频率计算及估计,具体流程如图5所示。只要信号噪声频率不在信号的真实频率范围内,便可以认为真实频率具有平移变换不变性,而本算法的研究对象为高轨卫星CEI信号,其信号频率一般处于GHz量级。基于此,便可应用神经网络卷积结构,从频率表征模块的输出中提取出待估计信号的正弦分量数量,并进行精确的频率估计。

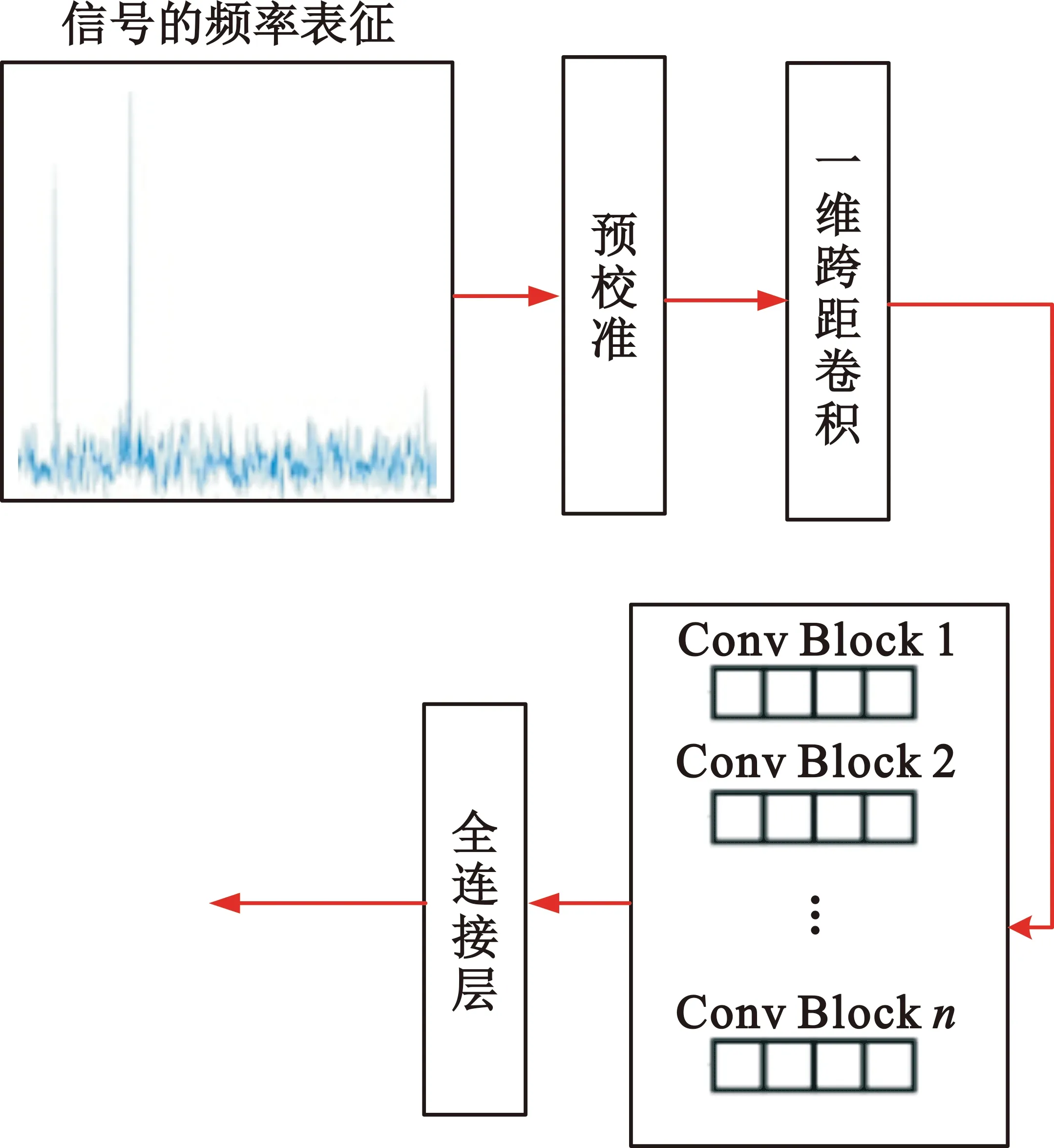
图5 基于深度学习的频率计算及估计模块具体流程

该模块将在一个训练数据集上进行预校准,该数据集包含由频率表征模块产生的FR函数实例。频率表征和频率数量计算模块分开训练,损失函数由频率数量计算估计值和真实数量之间的平方2范数差给出。

该模块中,首先将经过频率表征的CEI信号输入一个带有宽内核的初始化一维跨距卷积层,处理完毕后的数据将输入若干个带有局部滤波器的卷积块。然后,将处理完毕的结果输入全连接层,得到待估计的信号频率数量计算结果,最终可得到CEI信号频率估计的结果。

3 实验验证与分析

3.1 仿真参数设置

为验证本文提出算法的可行性、有效性和优越性,本文将在仿真条件下对算法的核心模块进行运行分析,在此基础上将本算法与前人研究的主流算法进行了比较。本文算法的核心模块仿真运行时以及各算法进行性能比较时的参数设置分别如表1和表2所示,表中(a:m:b)表示参数值从a取到b,取样间隔为m,如表1中的(-1∶1)表示频率从-1 GHz取到1 GHz。为充分仿真实际的高轨卫星CEI信号,仿真信号频率均取到GHz量级。本文的参数选取和设置主要着眼于所提出方法的应用场景,即高轨卫星的高精度CEI频率估计,因此所仿真的信号频率均在GHz量级,相关的神经网络层数也较好地适应这一应用需求和任务导向。

表2 算法的频率计算和估计模块仿真运行时的参数设置

如公式(5)所示,高轨卫星CEI信号中的各类噪声可近似为复高斯白噪声,服从N(0,σ2)分布。而对于初相角、幅度和频率均未知的复正弦信号,频率估计的克拉美罗界(Cramér-Rao bound,CRLB)和信噪比(Signal-to-Noise Ratio,SNR) 分别为

(8)

(9)

表3所列的仿真参数中,量化频率Δf满足

表3 各算法进行性能比较时的仿真参数设置

(10)

3.2 仿真条件下本算法各模块运行结果

本文在表1和表2所示的仿真条件下对算法的核心模块进行了运行和分析。

算法的频率表征模块在表1所示的仿真条件下进行了学习和训练,转置卷积层中的滤波器宽度设置为50,步长为16,以便在大小为2×103的网格上获得离散化的仿真信号的频率表征。训练中不断加入新的噪声,以提高对于信号中噪声的识别与表征水平。使用Adam优化器来最小化训练损失,初始学习率设置为3×10-4。Adam优化器通过对梯度的一阶矩估计和二阶矩估计进行综合考虑,计算出更新步长。它利用历史梯度平方的一阶指数平滑来解决梯度稀疏的问题:频繁更新的梯度将会被赋予一个较小的学习率,而稀疏的梯度则会被赋予一个较大的学习率。通过上述机制,在数据分布稀疏的场景能更好利用稀疏梯度的信息,相比于比标准的SGD算法可以更有效地实现收敛[26]。

频率表征模块训练完毕后的仿真测试结果如图6所示。测试使用的仿真信号带有两个正弦分量,为充分反映本模块相比于传统算法的优越性,仿真信号的两个正弦分量的幅度相差10倍,信噪比分别取1,5 dB,10 dB,100 dB。在每一个信噪比条件下进行10 000次蒙特卡洛仿真,仿真信号的相位和具体噪声值随机变化,变化服从标准高斯分布,将每100次频率表征结果取平均值。

图6 频率表征模块仿真测试结果

由图6可见,在每一信噪比下,本模块均能成功分辨出信号的两个正弦分量,且在其中一个分量幅度相当小,噪声值很大时依然可以检测到信号频率并实现频率表征,相应峰值的幅度有所下降,这充分表明了频率表征模块的有效性。

算法的频率计算与估计模块在表2所示的仿真条件下进行了学习和训练,初始层内的滤波器大小为50,步长为10,将输入降采样到长度为400的特征向量中,共10组采样序列,每组长度均为4 000。该模块的训练数据产生方式如下:将上一模块的训练数据输入具有固定、校准权重的频率表征模块后进行生成。同样使用Adam优化器最小化训练损失,初始学习率设置为3×10-4。

图7 频率计算与估计模块仿真测试结果

3.3 算法性能分析

为充分分析本文算法的性能,基于本文算法(记为DLFE)、Rife算法[11]、Quinn算法[12]、AM算法[13]、联合DFT和二分算法[14](记为DFTD)、两点细化法[15](记为TPR),在表3所示的仿真条件下进行了10 000次蒙特卡洛实验。测试信号为带有复高斯白噪声的正弦信号,仿真频率fk2为20～30 GHz,间隔步长1 GHz;信噪比SNR3取-20～12 dB,间隔步长2 dB。本文算法各模块的训练平台为NVIDIA Tesla V100,训练时长为11 h。

本文采用的算法性能评价指标为均方根误差(Root Mean Squnre Error,RMSE)和频率插值方向误判率,公式分别如下:

(11)

(12)

式中:K为频率估计总次数;fi0为信号真实频率;fie为算法估计频率;Ke为发生频率插值方向误判的次数。

图8和图9分别给出了不同信噪比下各算法的频率估计均方根误差和频率插值方向误判率。

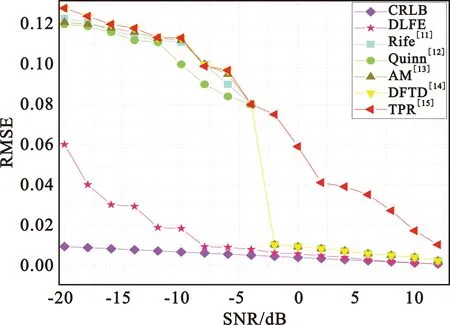
图8 各算法在不同信噪比下的频率估计均方根误差

图9 各算法在不同信噪比下的频率插值方向误判率

由图8可知,信噪比大于-6 dB时,本文算法的估计精度便较为逼近CRLB;相比之下,信噪比大于-2 dB时,四种改进算法的估计精度才实现了大幅提高,逐渐逼近CRLB,且信噪比在(-20 dB,-2 dB)内时,本文算法的估计精度远高于原始Rife算法和四种改进算法,最高为10.02倍。

由图9可知,由于进行了充分的学习和训练,本文算法基本避免了传统频率估计算法的最大误差来源——频率插值方向误判,从而大幅提高了进行频率估计的精度,这在强干扰、低信噪比的高轨卫星CEI测量这一实际运用场景中尤为重要。相比之下,Rife算法和AM算法在较低的信噪比下均存在较为严重的频率插值方向误判,其他三种改进算法大幅修正了该误差,但与本文算法仍存在一定差距。

表4给出了传统方法与本文提出的方法在运行时间上的对比结果,可以看出,连续5次测试中,由于在频率表征和频率计算及估计这两大核心模块中采用了GPU进行加速处理,使得本文所提方法(DLFE)的运行时间始终维持在0.653～0.714 s范围内;相比之下,传统方法由于需要进行大量的重复性频率估计策略的运算,导致总体运行时间较长,且由上文可知其估计精度也不如本文所提方法,这体现了运用基于深度学习的频率估计方法在保持较高的频率估计精度的基础上运行时间较短这一优势。