相控阵测控技术(四):相控阵测控中角误差对测速/测距误差的耦合效应*
2023-11-25刘嘉兴李增有
刘嘉兴,李增有
(1.中国西南电子技术研究所,成都 610036;2.中国人民解放军91550部队,辽宁 大连 116023)
0 引 言
相控阵测控系统相比于一般相控阵的主要区别是要实现高精度的测速、测距和测角[1-3],其测速、测距是通过测量合成载波相位来实现的。而相控阵是控制阵元通道的相位来实现角度扫描与角跟踪的,当阵元通道相位变化时,将会同时影响合成载波的相位值,从而影响测速、测速数据,因此角度误差将会引起测速、测距误差,角度变化将会引起速度/距离值的变化,本文将这种现象称为相控阵测量的角度差对测速/测距误差的耦合效应。这是相控阵应用于测控系统的特殊技术问题,实际上涉及一个重要议题,即相控阵能否用于具有高精度测速/测角/测距要求的测控系统中。
由于目标角运动才会去控制移相器相位变化使波束对准目标,因此研究的重点是目标运动及其角跟踪时对合成载波相位的影响。当跟踪静止目标时相控阵移相器相位不变,它就等同于一个机扫天线系统,将不会存在上述问题。
1 产生的机理
作为基础,先分析线阵情况,如图1所示。
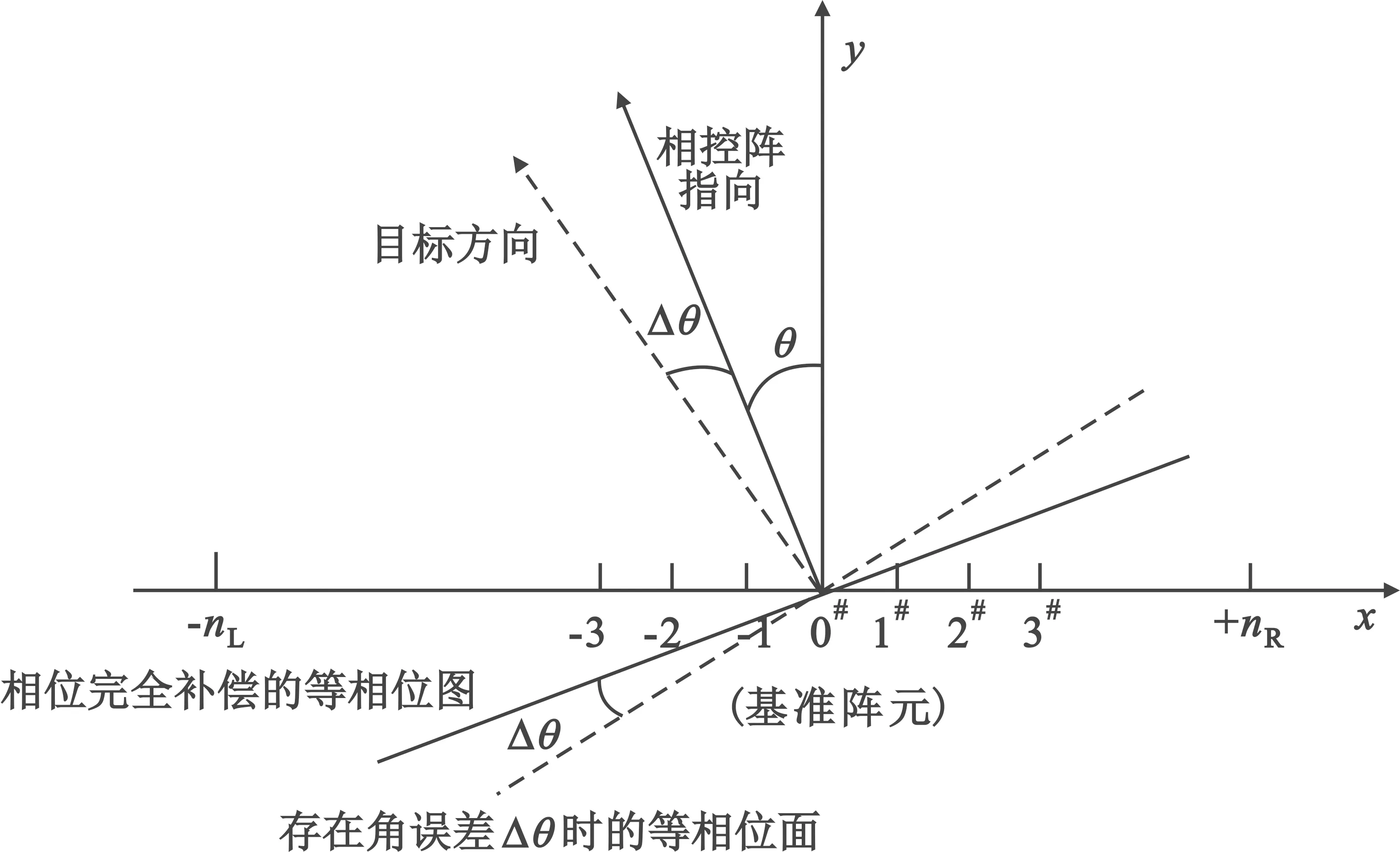
图1 线阵及其基准阵元
为不失一般性,可任选阵中某一阵元作为配相的基准阵元,以其输出信号的相位作为基准,其他阵元配相到与其同相,完成同相相加。图1中0#阵元为基准阵元,它与oxy坐标的原点重合,其右侧有nR个阵元,左侧有nL个阵元,nL>nR,它们构成两个子阵(在角跟踪时作为两个测角子阵)[4],阵元间间隔为D。在oxy坐标中相控阵的理想指向为θ,目标实际方向为(θ+Δθ),相差Δθ,这时相控阵的阵内移相值未能完全补偿目标信号的空间相移。在下行接收时,它使各阵元通道接收的输出信号不同相,阵元通道间依次递加一个相位差值φΔ。对于几何理论模型
φΔ=φ2-φ1。
(1)
式中:φ1为指向角θ时阵元间配相的相对相移递增值,用相位干涉测量的几何理论模型计算为
(2)
式中:λ为来波信号波长。
当目标方向为(θ+Δθ)时,来波的空间相移值
(3)
则
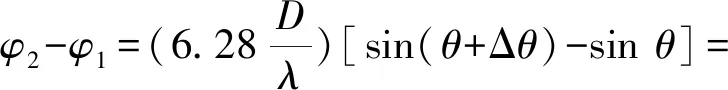
(4)
当Δθ<<2θ时,
(5)
式中:φΔ的单位为rad;D和λ的单位为m。上式给出了当目标偏离指向轴Δθ时引起的相邻阵元通道输出信号的相位差。
在假定各阵通道输出信号幅度相同为U,基准阵元相位为0°时,基准阵元的输出信号为
U0(t)=Ucosωt,
(6)
右边nR个阵元通道的合成信号为
(7)
上式可用三角函数和差化积进行多次二合一运算,准确值可由计算机仿真计算求得。在nR≫1时,可得到近似的单项表达式为
(8)
上式说明,右子阵合成载波的相位相对于基准阵元信号的相位偏移了φR=(nR+1)φΔ/2。
左侧nL个阵元的阵内相位差是-φΔ,合成载波信号ULΣ(t)为
(9)
左子阵合成载波的相位偏移为
φL=-(nL+1)φΔ/2。
全阵总的合成信号输出为
uΣ(t)=URΣ(t)+ULΣ(t)+U0(t) 。
(10)
为了使表达式更简单,更易理解其物理意义,在nR与nL比较接近,阵元数比较多时,将幅度近似为
(11)
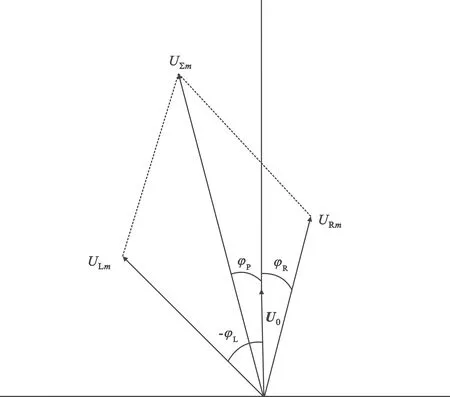
又由于U0< (12) (13) (14) 式中:φP为合成载波相移,它是由于采用相控阵测控方案后,产生的合成载波相对于基准阵元载波的附加相移,这个附加相移产生附加测距误差,附加相移随时间变化则产生附加测速误差;UΣm为合成载波幅度。 以上是基于时域内对各阵元输出相加的瞬时电压表达式来进行的分析,为使表达更直观,并与角跟踪的两测角子阵相联系,可采用对两子阵输出信号的相量分析法。这时两子阵输出信号的相量合成图如图2和图3所示,图2为两子阵输出信号相位奇对称时的两相量合成图,图3为两子阵输出信号相位非奇对称时的两相量合成图。 图2 两子阵输出相位奇对称时的相量合成图 图3 两子阵输出相位非奇对称时的相量合成图 图2纵坐标表示相量的相位为0°,横坐标上为90°。图中以基准阵元信号的相量U0为基准,其相位为0°,位于纵坐标轴上(也就是以各阵元与基准阵元同相相加的合成信号相量为基准),左子阵合成信号的相位为-φL,右子阵合成信号的相位为φR。由于两子阵输出信号的相位奇对称,即绝对值φR=φL,符号相反,幅度又近似相等,而且又是按基准阵元相位为基准配相的,所以合成相量与基准阵元同相,幅度减至UΣm。由图3可见,合成相量偏离了一个角度,产生了合成载波附加相移φP,幅度衰减至UΣm。φP可按图3的相量合成图求得 (15) 从图2、图3和式(13)可以看到,当nR=nL时(即两子阵对称时),即使存在角度误差Δθ,φP都会为0,不会使合成载波附加相移φP。表示在图2的相量图上,即使不同的Δθ使子阵输出信号产生了不同相移φL1,φL2和φR1,φR2,但由于左、右子阵输出信号的相移是数值相等而符号相反的(即奇对称φR1=φL1,φR2=φL2),它们的合成载波矢量仍在基准阵元相量的方向上,没有附加相移φP。而当nL≠nR时,从公式(13)可见,Δθ的存在会使φP不为零,使合成载波产生了附加相移φP。表示在图3上,由于φR≠φL,使合成矢量偏离了基准阵元相量的方向,即合成载波产生了附加相移φP,它可由式(15)计算。 从图3还可看出,在不作式(11)的近似(UL≈UR)时,UL将更大,附加相移φP将更大。 上述分析说明,由于两子阵阵元数不等而形成的两子阵布阵不对称时,角度误差将会引起合成载波的附加相移。实际上除阵元数外,影响两子阵输出不同相的因素还很多,包括: 1)两子阵布阵不对称(包括阵元数、布阵图形、各阵元相位中心的距离和高度、安装精度等):它们会导致两子阵输出信号的相位不奇对称和幅度不等。 2)两子阵阵面不对称:它会导致两子阵阵外信号的相位延迟不对称,使两子阵输出信号的相位不奇对称和幅度不等。这在曲面阵中较为严重。 3)两子阵的相控阵扫描特性不对称:这是由阵元间互耦、边缘效应、多径反射、阵内阵元方向图变化等因素引起的不对称[5],譬如平面阵时,阵面左边沿互耦较弱,阵中间互耦较强,右边沿的互耦又较弱,当波束由左向右扫描时,左子阵的互耦影响由弱到强,右子阵则由强到弱,正好相反,致使扫描特性不对称。 4)各阵元通道的相移、增益不一致引起两子阵输出的相位不奇对称和幅度不等:它会引起测距附加误差,但随时间慢漂移,不会引入测速附加误差。不过,当它引起两子阵输出相位不等而产生相位差时,合成载波的相位将与两子阵的输出幅度相关,会引起测距附加误差。如果这个幅度随时间变化,则合成载波的相位也会变化,带来附加测速误差;相反,如果两子阵输出没有相位差,是同相相加,则两子阵输出幅度的变化不会带来测距、测速附加误差。 5)模型误差:上面的分析是基于几何关系得出的空间相移的理论关系,但实际的有源相控阵是电磁场+电路的结合,使得阵元间相移差的实际模型会偏离几何理论模型,使两子阵输出信号的相位和幅度偏移理论值。 6)基准阵元没有安装在阵面中心,它直接带来两子阵不对称,而一般关于相控阵的文献中是以端点阵元作为基准阵元进行配相的,这与对称设计的思路大不相同。 上述不对称因素可以综合起来用不对称因子A来代替nR-nL,则式(13)变为 (16) 以上因素为A在物理上的含义,其中有的因素可以通过仿真计算得到,但有些因素实际上很难计算,不过它在电性能上的相应表现是两子阵输出载波的相位不奇对称和幅度不等,因而可以通过测量两子阵输出的相位差和幅度来获得不对称因子。在工程实践中,主要是尽量减少物理上的不对称因素以减小A,并对两子阵输出进行相位一致性校准。 以上讨论的均是下行接收时合成载波附加相移情况。上行载波是空间合成,合成载波相位偏移的机理与下行相同,可采用类似的分析方法。 下行的单向附加测距误差为[6] (17) 在测控系统中,主要采用测距信号(测距音、伪码等)测距,这时系统的群时延将会引起测距误差,而相控阵天线部分引起的时延是相时延,在同一个系统中,相比起来其比测距信号群时延引起的测距误差要小,是次要成分。但在测控系统中,对测速精度要求很高,载波相位变化引起的测速误差则是一个重要的测速误差源,它引起的单向附加测速误差由下式决定[6]: (18) φP(t)中包含Δθ(t),θ(t),λ(t)三项可随时间变化的因素,它们对时间微分就可得到各自引起的测速误差。 1) 角度误差变化Δθ(t)(包括闭环的角跟踪误差和开环的角指向误差)[7] 由式(16)对Δθ(t)微分可得 (19) 式(19)表示的是当系统工作在某一指向角θ和工作波长λ时,由于相控阵指向与目标方向的角度差Δθ(t)随时间变化而引入的附加测速误差,包括闭环角跟踪误差随时间的变化或开环引导时引导误差随时间的变化等引起的测速附加误差。 2)目标角运动θ(t) 目标角运动方程为 (20) 由式(16),对θ(t)微分可得 (21) 3) 信号多普勒频率变化 由式(16)对λ微分可得 (22) 式(22)表示的是当角跟踪误差Δθ和天线指向角θ不变时,载波频率的变化将使阵元间间隔偏离设计时的电长度,从而带来φΔ,使合成载波相位偏移。此偏移随载波多普勒频移变化而变化,从而引入附加测速误差。由于载波多普勒频率较小,此项误差一般较小。 除合成载波附加相位变化引入测速附加误差外,合成载波幅度减小会减小信噪比,从而增大测速、测距随机误差。由于相位补偿误差φΔ使左子阵合成载波的相位偏移了-φL,右子阵合成载波的相位偏移了+φR,由图3可求得两子阵合成载波的幅度UΣm为 (23) 它使合成载波的电压信噪比下降,下降因子为 (24) 由于测速、测距的热噪声随机误差反比于电压信噪比[8],所以其随机误差增大因子为1/Lφ。在实际工程中给出了具体参数后,就可利用上述公式计算出具体的测速、测距误差,在此不再赘述。 归纳起来讲,当相控阵天线的指向偏离目标方向Δθ时,它使阵内相移不能完全补偿空间相移,产生相位补偿误差φΔ,在两子阵不对称时,它可使合成载波产生附加相位偏移和幅度衰减,从而导致测速、测距附加误差,使总的系统误差和随机误差增大。 这个传递链路可表示为图4。 图4 角度误差→测速/测距误差的传递链路 从图4可以看到,角度的变化引起速度值和距离值的变化,于是将这个链路概括为角度差对测速/测距误差的耦合效应,其源头Δθ的产生原因,笔者已在文献[7]中进行了介绍。从图4还可看出,减少Δθ可以减少测速、测距误差。 以上分析说明,当相控阵天线指向偏离目标方向Δθ时,若两子阵输出相位非奇对称,将引起合成载波附加相移,从而产生附加测距误差;若载波附加相移随时间变化则会产生附加测速误差。相比于机扫天线而言,产生这些附加误差是由相控阵的两个特点所引起的:一是用控制相位变化实现角跟踪和角扫描;二是相控阵存在非恒值的相位扫描特性和幅度扫描特性。 由于目标角运动才会有角跟踪和角扫描,因此由目标角运动引入的这种附加测速、测距误差将是需研究的主要问题。 由于篇幅所限,本文所述耦合效应所引起的测速/测距误差的定量分析以及减小该误差的措施将在后续论文中具体介绍。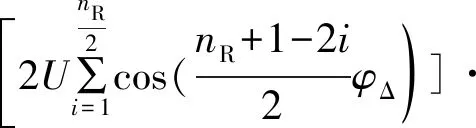
2 引起两子阵不对称的其他因素
3 附加相移φP引起的测距、测速附加误差
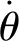

4 结束语
