电离层虚高误差影响下基于神经网络的单站定位结果修正*

祝志聪,张 莉,王 鼎,邓 杰,高卫港

(信息工程大学 信息系统工程学院,河南 郑州 450001)

0 引 言

超视距(Over-the-Horizon,OTH)目标的高精度定位是空间目标监测和导航领域中的一个关键问题。直接位置确定(Direct Position Determination,DPD)[1-3]克服了两步位置方法的缺点,显著提高了在低信噪比条件下的定位性能。通过建立接收到的信号模型,DPD根据最大似然准则直接从信号数据中获取信息。DPD还可以将通道信息(如电离层结构)集成到位置估计模型中。

在基于到达角(Angle of Arrival,AOA)的DPD方法[4]中,常用的有多重信号分类[5](Multiple Signal Classification,MUSIC)和子空间拟合方法等。实际的OTH场景极其复杂,短波通信往往依赖于电离层反射,此时要想利用MUSIC算法或者子空间拟合方法进行定位,则需要获知电离层信息,而复杂的电离层特性使得现有的定位算法难以模拟复杂的信道场景,因此即使使用目前先进的DPD算法,OTH定位仍然面临着巨大的挑战。

在解决超视距直接定位中的电离层问题上,文献[6]提出了一种电离层虚高观测误差存在条件下的超视距直接定位算法,将电离层虚高观测量误差的影响引入目标的定位优化模型中,利用最大似然准则建立目标函数,对目标位置和电离层虚高参数进行联合估计;文献[7]提出了一种基于已知辐射源信号波形的超视距目标直接定位方法,降低了在电离层虚高观测误差的情况下的定位误差。以上文献都对将电离层虚高误差的变化视为高斯分布,这种分布的前提是虚高测量误差在一个较小的阈值内,并且实际情况下误差的分布并不一定是零均值的。

与此同时,学者们也开始利用一些神经网络方法解决电离层模型误差下的定位问题。2020年,Yu等人[8]提出了一种基于双向长短期记忆(Bidirectional Long Short-Term Memory,BiLSTM)网络框架的深度学习定位方法。该方法利用BiLSTM直接对接收到的信号数据进行处理,降低了电离层虚高误差对定位的不利影响。受此启发,本文提出了一种基于神经网络的单站定位电离层虚高误差校正方法,利用神经网络学习存在电离层虚高误差情况下的MUSIC算法直接定位结果与目标真实位置之间的非线性映射关系,从而降低电离层虚高误差对定位精度的影响。与文献[8]直接对接收到的信号数据进行处理的方法相比,本文方法虽然在一定程度上需要准备训练数据的时间更多,但在网络复杂程度和训练难度上更低。

1 定位场景

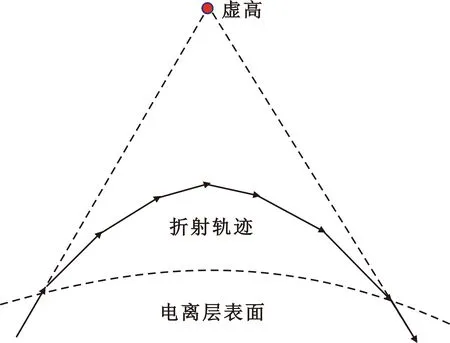
图1 短波信号在电离层中的折射现象

超视距目标单站定位就是运用射线反跟踪原理,利用一台能够测量二维角度(方位角和仰角)测向机器,结合短波信号在电离层中的反射虚高,确定出辐射源的位置。图2为场景示意图。

图2 超视距目标单站定位场景

(1)

(2)

(3)

(4)

(5)

(6)

考虑整个实验过程是在较短的时间内完成的,可以认为在这个时间段内电离层参数没有发生变化。对于某一个频率确定的信号,在电离层中反射虚高是随信号位置变化而变化的,因此可以用一个连续的不规则曲面来模拟信号在某个区域的电离层反射虚高,如图3所示。

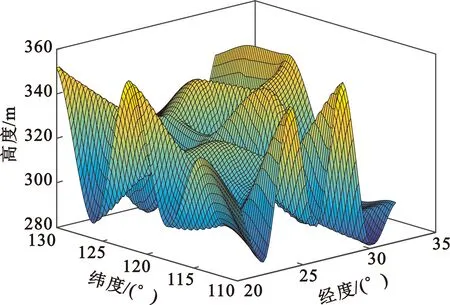
图3 电离层反射虚高模型

在实际的定位环境中,一般根据接收到的信号频率等参数,利用垂直离子探空仪对反射虚高进行测量。虽然该探测技术目前是比较成熟的,但电离层的电子密度是随地域发生变化的,探测点的位置往往不是反射点,因此反射点虚高的观测值往往存在误差。

2 方法提出

2.1 基于MUSIC算法的直接定位

相比于均匀面阵,均匀圆阵能够利用更少的阵元实现对信号二维角度的估计。假设利用半径为r的M元均匀圆阵对波长为λ的短波信号进行接收和采集,阵列接收信号模型为

x(c)(t)=a(α(c),γ(c))s(c)(t)+ξ(c)(t)=

在确定评估指标后，采用专家打分法对评估指标之间的重要程度进行比较量化。一般的，将比较结果分为5个等级：相同、稍强、较强、很强和绝对强，并且用1～9来表示。通过专家打分对评估指标的重要性进行判定，构造一级评估指标的判断矩阵，如表2。

b(θ(c),β(c))s(c)(t)+ξ(c)(t)。

(7)

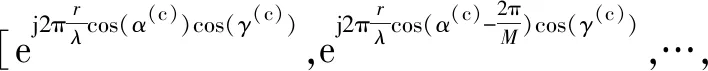
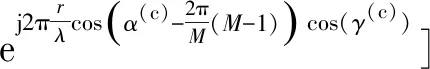
(8)

根据阵列采集的信号样本x(c)(t),根据式(9)构造协方差矩阵:

(9)

(10)

(11)

Pmusic的最大值(谱峰)所对应的经度θpeak和纬度βpeak就是对信号位置的估计。

2.2 电离层虚高误差对定位精度的影响

电离层虚高导致的定位误差模型如图4所示。

图4 电离层虚高误差模型

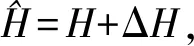
(12)

当仰角准确时,电离层虚高误差ΔH引起的地面距离误差Δd可以表示为

(13)

(14)

设置辐射源所在位置为东经128.5°,北纬20.5°;测向站所在位置为东经111.23°,北纬30.47°;电离层虚高真实值为320 km。利用MUSIC算法估计信号源位置,定位误差随电离层虚高观测值的变化曲线如图5所示。由图可知,在观测站和信号源距离约1 700 km时,20 km的电离层虚高观测误差可以造成约100 km的定位误差。

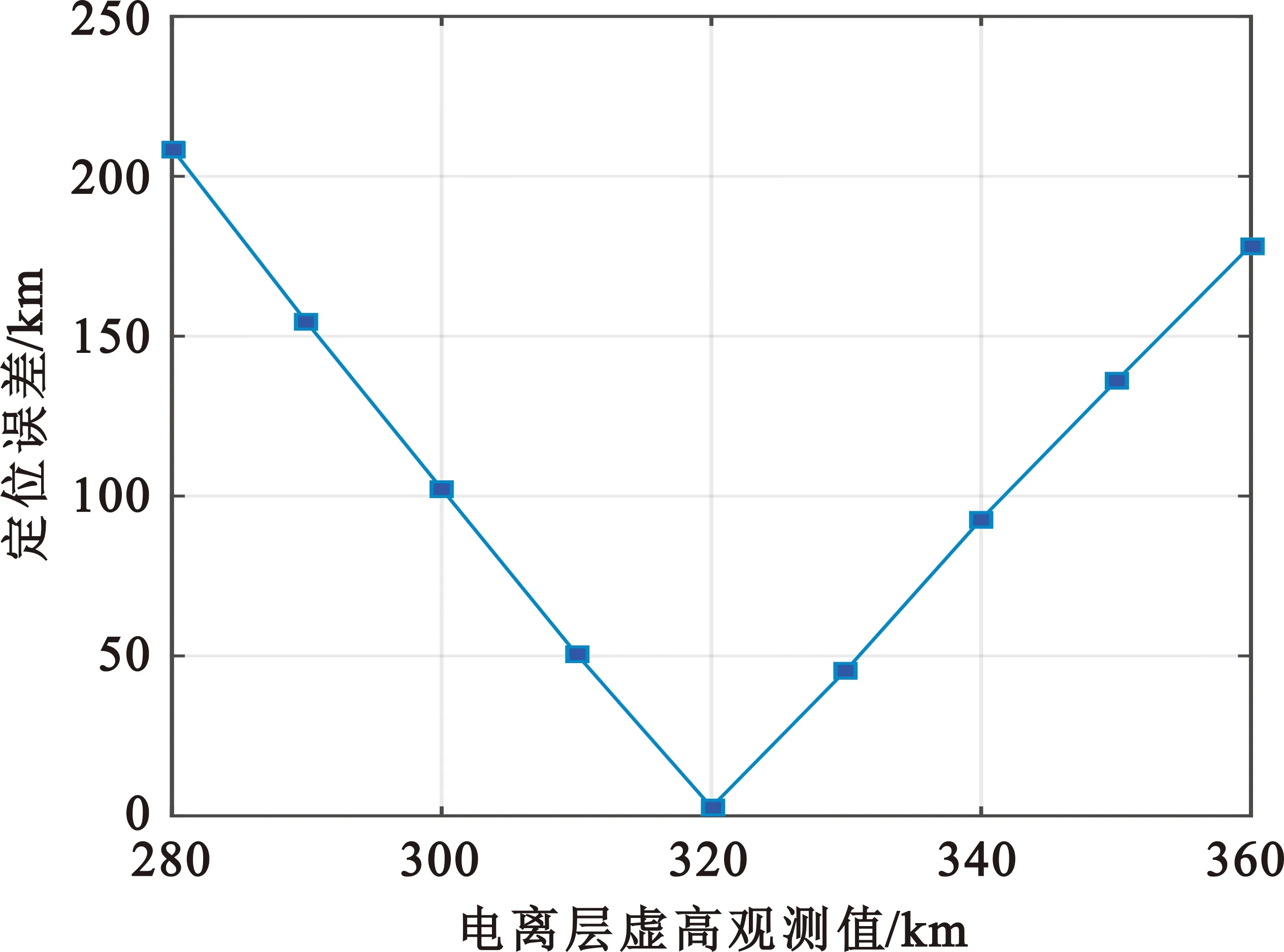
图5 定位误差随电离层虚高误差变化曲线

2.3 方法框架

基于以上分析可以得出结论:电离层虚高误差会使得MUSIC算法的定位结果与真实位置存在一定的偏差,由于电离层反射虚高随地域变化的特性,该偏差与信号所处位置有着密切的关系。因此可以利用神经网络善于处理非线性问题的优点,在定位区域放置若干个样本信号源,学习这些样本MUSIC算法定位结果与真实位置之间的非线性映射关系,从而对未知信号利用MUSIC算法定位结果的偏差进行校正。

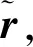
图6 方法框架

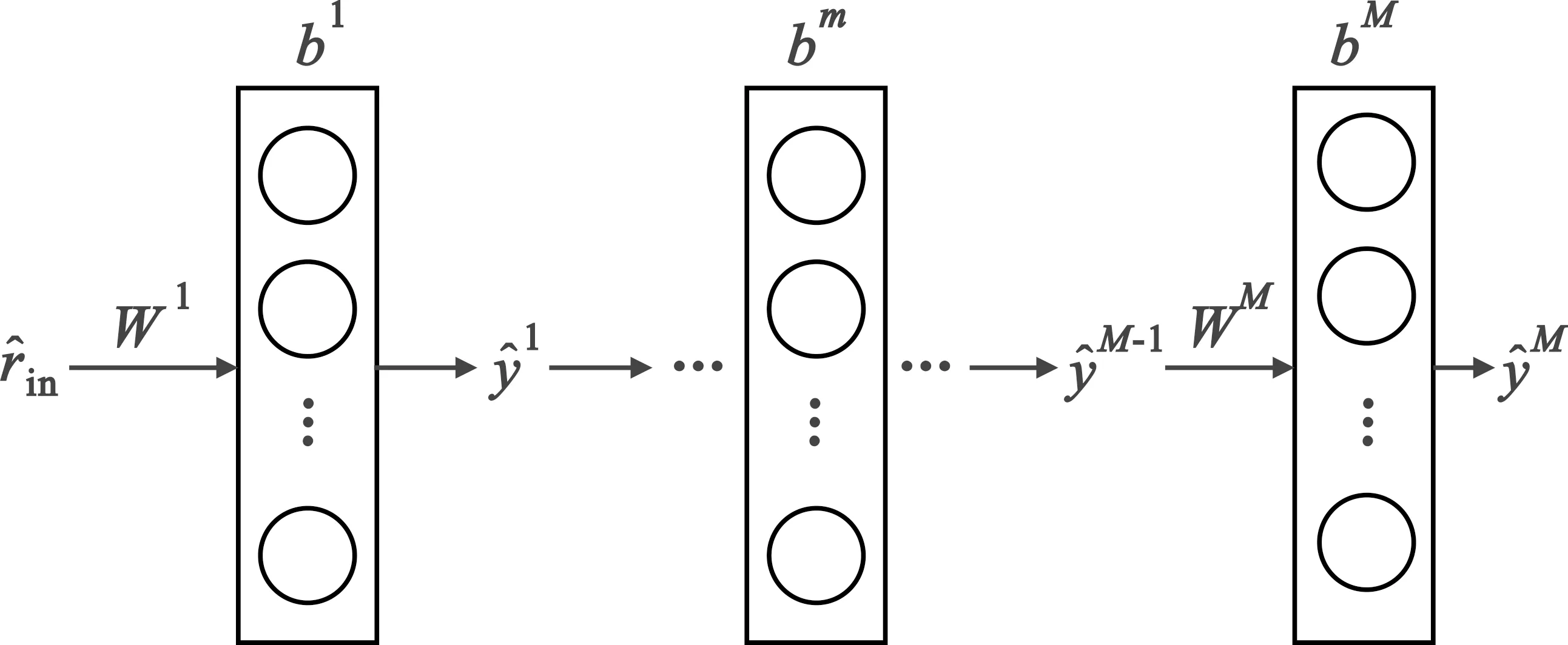
图7 神经网络结构

(15)

式中:Wm和bm分别表示第m层的权重矩阵和偏差向量。

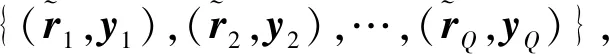
(16)

3 仿真实验

3.1 仿真条件

在仿真分析中,使用了9元均匀圆阵来估计信号源的位置,圆阵半径为波长的2倍;信号源的频率为10 MHz,快拍数为1 000,收集样本信号时信噪比设置为0 dB,对信号源重复收集5组信号。观测站位置p设为东经111.23°,北纬30.47°;定位区域设为东经120°～130°,北纬20°～30°;电离层虚高的观测值固定为320 km。仿真实验所建立的神经网络为全连接方式,其结构参数如表1所示。

表1 网络结构

本文使用一个随机拟合的曲面(高度分布在[280 km,360 km])来模拟实际情况下某个频率确定的信号在电离层中的反射高度的空间分布,假定反射是几何对称的。假设信号源所在位置为q,则其对应的电离层高度为hc=fc((p+q)/2)。

为了防止过拟合现象,将目标区域均匀的划分为若干个子区域(灰色虚线),在每个子区域随意放置同样数量的训练样本(蓝点),然后在目标区域随机选择位置放置验证样本(红色圆圈),训练样本和验证样本的数量比例为10∶3;最后在目标区域选择5个位置放置测试样本(红色星号),如图8所示。

图8 训练样本分布

其中5个测试集的位置如表2所示。

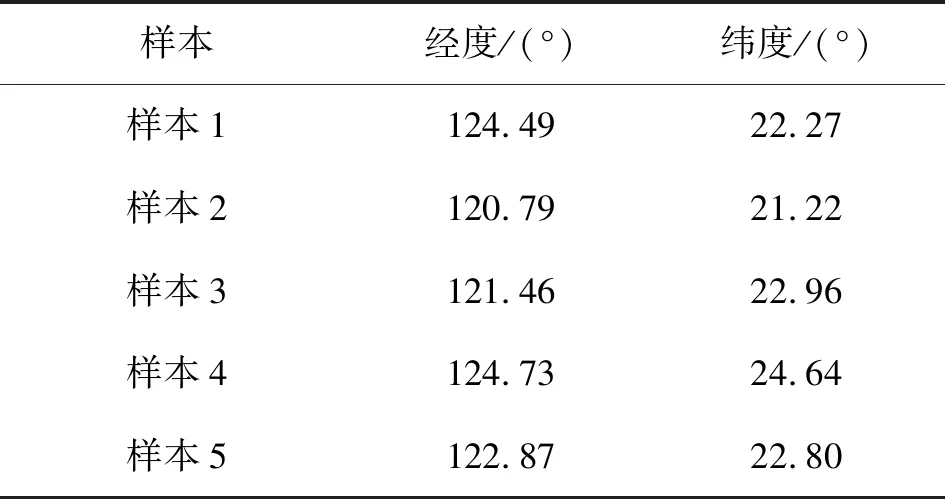
表2 测试集样本位置

仿真实验使用均方根误差作为方法的性能指标,其定义如下:

(17)

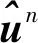
3.2 算法功能验证

在训练样本为100和信噪比为0 dB的情况下,对5个测试目标进行100次的蒙特卡洛实验,结果如图9所示。由图可知,虽然5个样本所在位置不同导致了校正效果的不同,但在蒙特卡洛实验中均表现比较稳定,定位精度大大提高。其中,样本5校正效果相对较好,50%和80%的定位误差分别在6.041 km和12.67 km内;样本4的校正效果相对较差,50%和80%的定位误差分别在12.21 km以内和21.97 km以内。

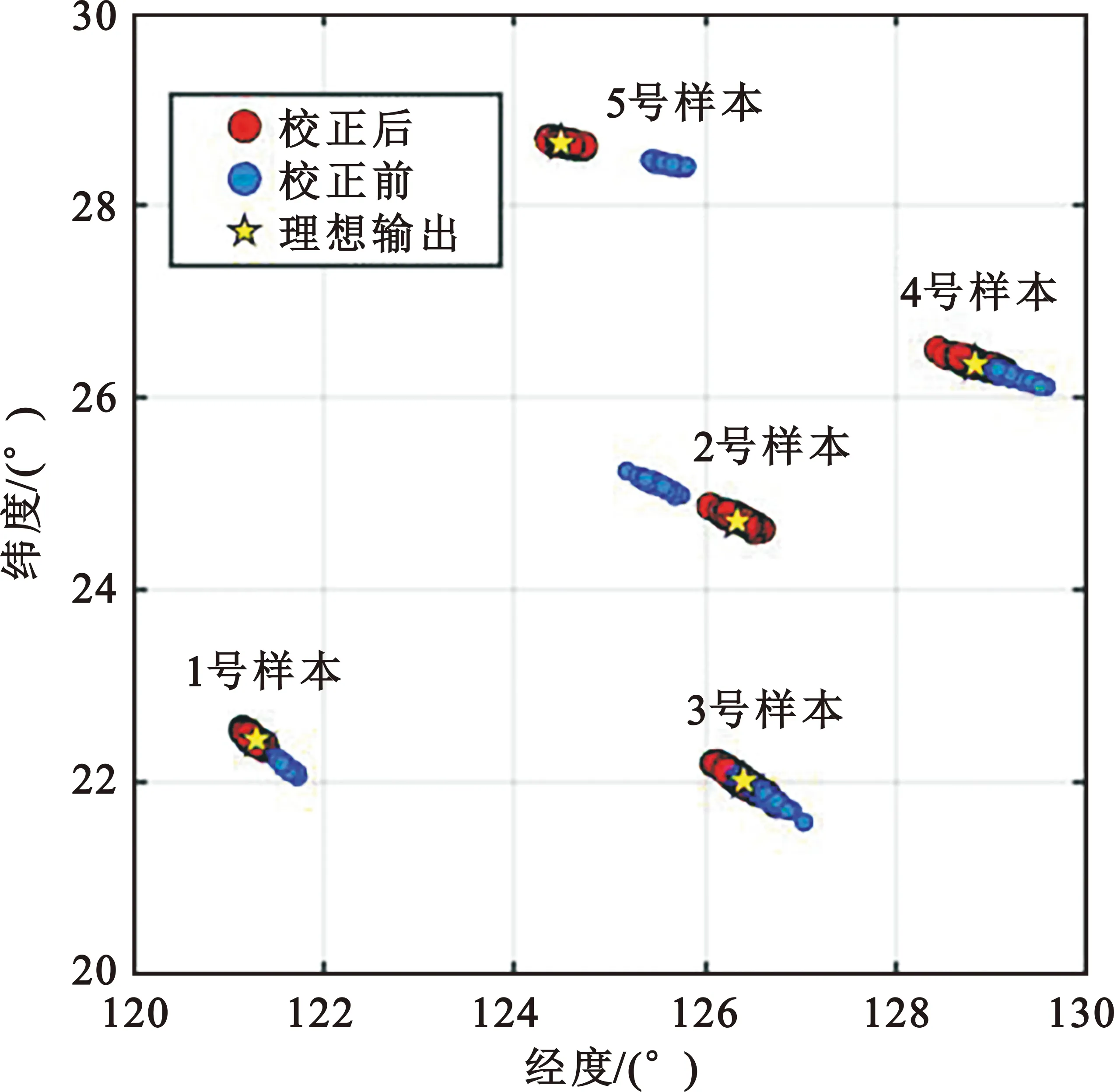
(a)5个测试目标100次的蒙特卡洛实验结果

4 结束语

本文首先建立了超视距目标单站定位模型和随空间发生变化的电离层虚高模型,对电离层虚高误差进行分析,发现电离层虚高误差会大大降低定位的精度。为了减小该误差,建立了一个基于神经网络的超视距目标单站定位结果校正方法,利用神经网络学习“虚假”位置和真实位置之间的关系,从而提高定位精度。最后利用仿真验证了该网络的功能。

本文为超视距定位提供了一种新的方法和实验基础,但还有许多问题需要进一步研究,比如怎样选择尽可能少的样本位置,以获得较高的定位精度。