基于上下文定界的Fork／Join并行性的并发程序可达性分析＊

钱俊彦，贾书贵，蔡国永，赵岭忠

（1.桂林电子科技大学计算机科学与工程学院，广西 桂林 541004）；2.并行与分布处理国家重点实验室，湖南 长沙 410073）

1 引言

无论从理论，还是实践角度来看，并发程序验证都是极具挑战性的问题。随着多核技术日益发展，通过引入Fork／Join并行性，并发程序将任务分解为更细粒度的子任务并行执行，从而充分利用多核处理器提供的计算性能［1］。但是，多个线程之间的交错执行可能会产生隐匿的错误和漏洞，故保证并发程序的正确性具有十分重要的意义［2］。近些年提出的上下文定界方法是一种适合并发程序的分析技术，其思想是仅考虑有限次上下文切换（控制权从一个线程切换到另一个线程）之内程序执行的计算。由于在有限次上下文切换之内可发现许多并发相关的错误，上下文定界思想有助于程序分析。在程序中存在递归和过程调用的情况下，虽然被搜索的状态空间是无界的，但上下文定界可达问题是可判定的［3］。

针对Fork／Join并行性的并发程序进行可达性分析，主要基于以下考虑：Fork／Join 并行性涉及到动态线程创建，而动态线程创建对于构建操作系统的组件是非常重要的［4］。例如：（1）文件系统、设备驱动、无封装数据结构等软件模块的无界并发执行；（2）异步行为的生成：例如创建一个线程、回调函数等；（3）实现应用软件的并行化执行，充分利用多核体系结构的强大性能。

2 下推系统

3 并发下推系统

3.1 定界可达问题

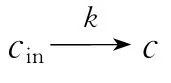
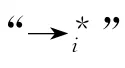
3.2 k－定界可达算法

Qadeer提出的上下文定界模型检验算法假设全局状态集合G 是有限的。算法执行过程中迭代地增加执行上下文的数目，在一个执行上下文内，全局状态对于当前线程是局部的，只有该线程可以访问全局状态。上下文切换时同步该全局状态，使得其他线程共享全局状态。对于给定正整数k，该算法可以搜索并发下推系统在k 次上下文切换执行所有可达的格局集合。k－定界可达算法如下所示：

算法1k－定界可达算法

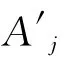
对于并发下推系统P＝（G，Γ，Δ0，…，ΔN，gin，win）和正整数k，该算法是可终止的，并且判定该问题的复杂度为O（k3（N｜G｜）k｜P｜5）。

4 Fork／Join并行模式的并发程序分析

随着多核处理器逐渐成为主流，并发程序通过引入Fork／Join并行任务调度模式，将一个规模较大的任务分解为更细粒度的子任务（线程）并行执行，从而充分利用多核处理器的计算能力。由于任务可以用线程的执行模拟，因此下文中用线程的概念来表示任务。

4.1 Fork／Join并行模式

Fork／Join并行模式是获取更高并行性能的最简单和高效的设计技术。Fork操作创建一个新的并行执行子线程，Join操作使得当前线程等待执行，直到新创建的子线程执行结束。图1给出了一个Fork／Join模式的示意图，位于图上部的线程依赖于位于其下的子线程的执行，只有当所有的子线程都执行结束之后，调用者才能获得线程0的返回结果。

允许Fork／Join并行模式的并发程序的线程标识符的使用是有限制的，因此对存储线程标识符的变量的使用也是有限制的。Fork操作创建一个线程标识符，存储在一个变量中。随后，该线程标识符被拷贝存储到其父线程的线程标识符变量中。最后，Join操作监视该变量中包含的线程标识符，该线程执行结束后返回父线程继续执行。

Figure 1 Fork／Join model图1 Fork／Join 模式示意图

4.2 动态并发下推系统

本节定义Fork／Join并行性的并发程序的抽象模型——动态并发下推系统。在并发程序中，各个线程模型可用新线程的下推系统来创建。线程包含局部变量并可访问全局（共享）变量。使用栈字母表Γ 模拟局部变量值，G 中的状态模拟全局变量的值。为了支持动态的Fork／Join并行模式，需使用存储线程标识符的程序变量对线程标识符进行存储。线程标识符取值于集合Tid＝｛0，1，2，…｝。新创建的线程标识符存储在其父线程的标识符变量中，父线程可对该变量中包含的线程标识符对应的子线程执行Join操作。

4.2.1 语法

一个动态并发下推系统可表示为一个七元组（G，Γ，Δ，ΔF，ΔJ，gin，γin）。其中：

（1）G 是所有全局变量赋值的（无限）集合，由包含布尔值的全局变量集合GBV 和包含线程标识符的全局变量集合GTV 组成。

（2）Γ 是所有局部变量赋值的（无限）集合，由包含布尔值的局部变量集合LBV 和包含线程标识符的局部变量集合LTV 组成。

（3）Δ⊆（G×Γ）×（G×Γ＊）是描述任意线程单个步骤的迁移集合。

（4）ΔF⊆Tid×（G×Γ）×（G×Γ＊）是Fork迁移关系。如果（t，〈g，γ〉，〈g′，w〉）∈ΔF，那么在全局状态g 下，栈顶符号为γ的线程创建一个标识符为t的线程，并修改全局状态为g′，栈顶符号γ 替换为w。

（5）ΔJ⊆LTV×（G×Γ）×（G×Γ＊）是Join迁移关系。如果（x，〈g，γ〉，〈g′，w〉）∈ΔJ，那么在全局状态g 下，栈顶符号为γ 的线程阻塞，直至标识符为γ（x）的线程执行完毕。一旦等待线程执行完毕，修改全局状态为g′，并将栈顶符号γ 替换为w。

（6）gin是初始全局状态，对于所有的x∈GTV，gin（x）＝0成立。

（7）γin是初始局部状态（栈内容），对于所有的x∈LTV，γin（x）＝0成立。

4.2.2 语义

定义1ss∈Stacks＝Tid →（Γ∪｛＄｝）＊是线程标识符对应的栈内容，C＝G×Tid×Stacks是动态并发下推系统的格局集合，⊆C×C 是动态并发下推系统格局上的迁移关系。

每个动态并发下推系统使用一个特殊符号＄∉Γ 来标记每个线程的栈底。动态并发下推系统的一个格局是一个元组〈g，n，ss〉，其中g 是全局状态，n是最后被创建的线程的标识符，ss（t）是线程t∈Tid 的栈。动态并发下推系统的执行从格局〈gin，0，ss0〉开始，其中对于所有的t∈Tid，ss0（t）＝γin＄。

以下规则定义了从格局〈gin，0，ss0〉开始线程t可以执行的迁移：

所有的规则都包含条件t≤n，表明线程t必须已经被创建。因此，只有线程0可以从初始格局〈gin，0，ss0〉开始执行。规则（I）允许线程t执行迁移关系Δ 中的一个迁移。规则（II）表示线程t终止执行，即当线程t的栈顶符号是＄时，线程t从栈中弹出符号＄，不改变全局状态，从而线程t终止执行。规则（III）模拟线程的Fork操作，即线程t根据一个Fork迁移关系创建一个标识符为n＋1的新线程。规则（IV）模拟线程的Join操作，线程t等待标识符为γ（x）的线程执行结束之后，线程t继续执行下一个迁移，其中γ 是线程t 的栈顶符号。使用一个空栈来表示线程终止。

4.3 简化为并发下推系统

本节说明如何将一个动态并发下推系统的k－定界可达问题转换为包含k＋1个线程的并发下推系统的k－定界可达问题。给定动态并发系统P 和正整数k，可以从中提取一个包含k＋1个线程的并发下推系统Pk，这些线程的标识符取值为｛0，1，…，k｝，并且足以验证Pk的k－定界执行。3.2节给出的算法可解决并发下推系统k－定界可达问题。

该简化方法的主要思想是：在一个k－定界执行中，至多k个不同的线程会执行一次迁移。可以使用Pk中标识符为｛0，1，…，k－1｝的k 个线程的迁移来模拟这k 个线程的迁移。Pk中的最后一个标识符为k 的线程从不执行迁移，该线程用于模拟P 中其它线程的存在。令Tidk＝｛0，1，…，k｝为整数k限定的线程标识符集合。AbsGk和AbsΓk分别是有限全局状态集合和有限局部状态集合，其中包含线程标识符的变量仅从Tidk中取值。

给定动态并发下推系统P＝（G，Γ，Δ，ΔF，ΔJ，gin，γin）和正整数k，可以构造出并发下推系统Pk＝（AbsGk× Tidk×T （Tidk），AbsΓk∪｛＄｝，Δ0，…，Δk，（gin，0，Ø），γin＄）。该并发下推系统Pk包含k＋1个线程。Pk的全局状态是一个三元组（g，n，α），其中g 是全局变量的赋值，n 是允许执行迁移的线程对应的最大线程标识符，α 是终止线程对应的线程标识符集合。初始全局状态是（gin，0，Ø），表明最初只有线程0可以执行一个迁移并且其它线程没有执行。

以下规则定义了线程t的迁移关系Δt上的迁移：

（I′）如果t≤n，（〈g，γ〉，〈g′，w〉）∈Δ，添加迁移（〈（g，n，α），γ〉，〈（g′，n，α），w〉）到Δt中。

（II′）如果t≤n，添加迁移（〈（g，n，α），＄〉，〈（g，n，α∪｛t｝），ε〉）到Δt中。

（III′a）如果t≤n，n＋1＜k，（n＋1，〈g，γ〉，〈g′，w〉）∈ΔF，添加迁移（〈（g，n，α），γ〉，〈（g′，n＋1，α），w〉）到Δt中。

（III′b）如果t≤n，（k，〈g，γ〉，〈g′，w〉）∈ΔF，添加迁移（〈（g，n，α），γ〉，〈（g′，n，α），w〉）到Δt中。

（IV′）如果t≤n，x∈LTV，（x，〈g，γ〉，〈g′，w〉）∈ΔJ，γ（x）∈α，添加迁移（〈（g，n，α），γ〉，〈（g′，n，α），w〉）到Δt中。

所有的规则都包含条件t≤n，表明从动态并发下推系统中选择的线程必须已经被创建。如果t＞n，线程t在格局〈（g，n，α），γ〉下没有可以执行的迁移。规则（I′）将Δ 中的迁移添加到Δt中。规则（II′）将栈为空的线程t添加到终止线程集合。规则（III′a）和规则（III′b）处理P 线程中的创建，是该转换方法中最重要的部分。规则（III′a）对应于新创建线程参与k－定界执行的情况。该规则将计数器加1，允许线程n＋1开始模拟新创建的线程。规则（III′b）对应于新创建线程不参与k－定界执行的情况。该规则保持计数器n 不变，从而保存Pk中现有的线程标识符。这两个规则将ΔF中创建线程的迁移关系添加到线程t 的迁移集合Δt中。规则（IV′）处理Join运算符，将所有先前终止线程的标识符都存储在α中。同时，该规则将挂起线程的迁移ΔJ添加到Δt中。

由动态并发下推系统P 构造并发下推系统Pk时，从初始全局状态（gin，0，Ø）开始，根据以上规则构造线程t（0≤t≤n＜k－1）可以执行的迁移关系集合。构造线程t的迁移关系集合Δt时，线程t的所有可执行迁移（包含Fork和Join迁移关系）均从动态并发下推系统P 的迁移关系集合中提取。当线程标识符t＝k时，构造过程终止，从而构造出模拟P 的k－定界执行的并发下推系统Pk。

5 结束语

本文给出了Fork／Join并行模式的并发程序的抽象模型——动态并发下推系统的定界可达性分析。通过将动态并发下推系统P 的k－定界可达问题简化为模拟其k－定界执行的并发下推系统Pk，从动态并发下推系统P 中提取的并发下推系统的k－定界可达性问题可使用现有的k－定界可达算法解决。能否直接对允许动态线程创建的并发程序进行可达性分析，及给出其求解算法，将是未来值得深入研究的问题。

［1］Lea D.A Java fork／join framework［C］∥Proc of 2000ACM Java Grande Conference，2000：36－43.

［2］Queille J，Sifakis J.Specification and verification of concurrent systems in CESAR［C］∥Proc of the 5th International Symposium on Programming，1981：337－351.

［3］Qadeer S.The case for context－bounded verification of concurrent programs［C］∥Proc of the 15th International Workshop on Model Checking Software，2008：3－6.

［4］Atig M F，Bouajjani A，Qadeer S.Context－bounded analysis for concurrent programs with dynamic creation of threads［C］∥Proc of the 15th International Conference on Tools and Al－gorithms for the Construction and Analysis of Systems，2009：107－123.

［5］Clarke E M，Grumberg O，Peled D A.Model checking［M］.Cambridge：MIT Press，2000.

［6］Autebert J M，Berstel J，Boasson L.Context－free languages and pushdown automata［M］∥Handbook of Formal Languages，New York：Springer－Verlag，1997：111－174.

［7］Schwoon S.Model－checking pushdown systems［D］.Munchen：Lehrstuhl fur Informatic VII der Technischen University，2000.