基于重叠联盟博弈的无人机侦察时间资源分配优化*
2023-11-25姚昌华韩贵真
姚昌华,韩贵真,安 蕾
(南京信息工程大学 电子与信息工程学院,南京 210044)
0 引 言
随着侦察任务的复杂化和多样化,单架无人机执行侦察任务时在目标识别准确率、计算能力、功耗、以及多任务点同时侦察等方面面临着巨大的挑战。在多无人机侦察系统中,其内部的多个无人机通过协同控制高效地执行侦察任务。多无人机侦察不仅具有较高的任务执行效益,而且具有较强的紧急情况应变能力,这些优点使得多无人机更适合在复杂环境下执行侦察任务[1-3]。
在多无人机执行侦察任务时,其中的关键就是对每个无人机进行合理的任务分配。文献[4]采用了一种特定的道路网侦察遗传算法来解决多无人机的任务分配问题。文献[5]提出了基于聚类算法的多无人机动态任务分配方法来实现多无人机侦察任务的合理规划。文献[6]提出了一种余弦相似性聚类方法(模拟退火)对大型多无人机系统进行任务分配。文献[7]提出了一种基于广域搜索场景的多无人机侦察任务分配模型,提高多无人机侦察任务分配效率。文献[8]在任务分配过程中考虑了用户对信息获取的满意度,提出了一种基于多群体合作的遗传算法解决了多项式时间内无人机的任务分配问题。文献[9]针对无人机群协同实时任务分配问题提出了改进合同网算法,在提高协商效率的同时也减少了通信量和通信频率。文献[10]提出一种基于改进共识的分组算法的任务分配算法,解决了协同异构无人机的任务分配问题。类似地,文献[11-15]分别采用了不同的算法来研究多无人机协同的任务分配问题。
在多无人机协同的任务分配问题中,时间资源优化是其中的重要部分。文献[16]提出了一种改进遗传算法,考虑不同任务的差异化时间约束,将多任务分配问题建模为带有时间窗约束的组合优化问题,有效地节省无人机使用的数量并降低总能耗。文献[17]在原有时间约束下模型中加入了威胁值的问题,通过一系列的约束条件来使得任务时间达到最小,以求得到最优的任务分配方案。文献[18]考虑了任务的优先级,将无人机执行任务所消耗的时间分解为飞行持续时间和悬停持续时间。文献[19]提出了基于时间窗的多无人机联盟组任务分配方法,以空闲时间窗为调度依据进行高效且实时的任务分配。
虽然上述文献运用不同的方法对任务分配的问题进行了研究,并且有的文献考虑了其中的时间资源优化问题。但是大部分文献未考虑无人机自身的时间资源,未考虑两个以上无人机同时执行同一任务时的时间分配问题。同时,大部分研究缺乏对侦察任务价值异构性的考虑。事实上,不同侦察任务重要程度往往不同,应当分配的侦察时间资源也需要优化。只有给每个侦察任务分配合理的时间资源,多无人机才能更加高效地完成侦察任务。因此,在多无人机执行侦察任务时,侦察任务的异构性和无人机的时间资源分配问题尚需进一步深入研究。
当前,无人机功能的异构性越来越明显,有的无人机可以同时执行多项任务。另外,有些重要任务的价值高、需求大,也需要多个无人机协同来提升该重要任务的执行效果。因此,无人机在任务分配过程中的交叉组合是实际需要的。基于以上考虑,为了更好地解决多无人机执行侦察任务时的时间资源分配问题,本文采用联盟博弈的方法[20],提出一种基于重叠联盟博弈的无人机侦察时间资源分配优化方案,将侦察任务的价值异构性考虑在内,研究如何将多个无人机的时间资源合理地分配给不同侦察目标的问题。
1 系统模型
系统模型如图1所示,有N个重要程度不同的侦察目标和M个无人机,且M>N。以侦察目标的数量来构建联盟,系统中有N个侦察任务则联盟数量为N。一个黑色圆圈代表一个联盟,联盟内的无人机命名为忙碌无人机。黑色圆圈外的无人机命名为空闲无人机,其旁边的矩形代表该无人机3个时间比例。
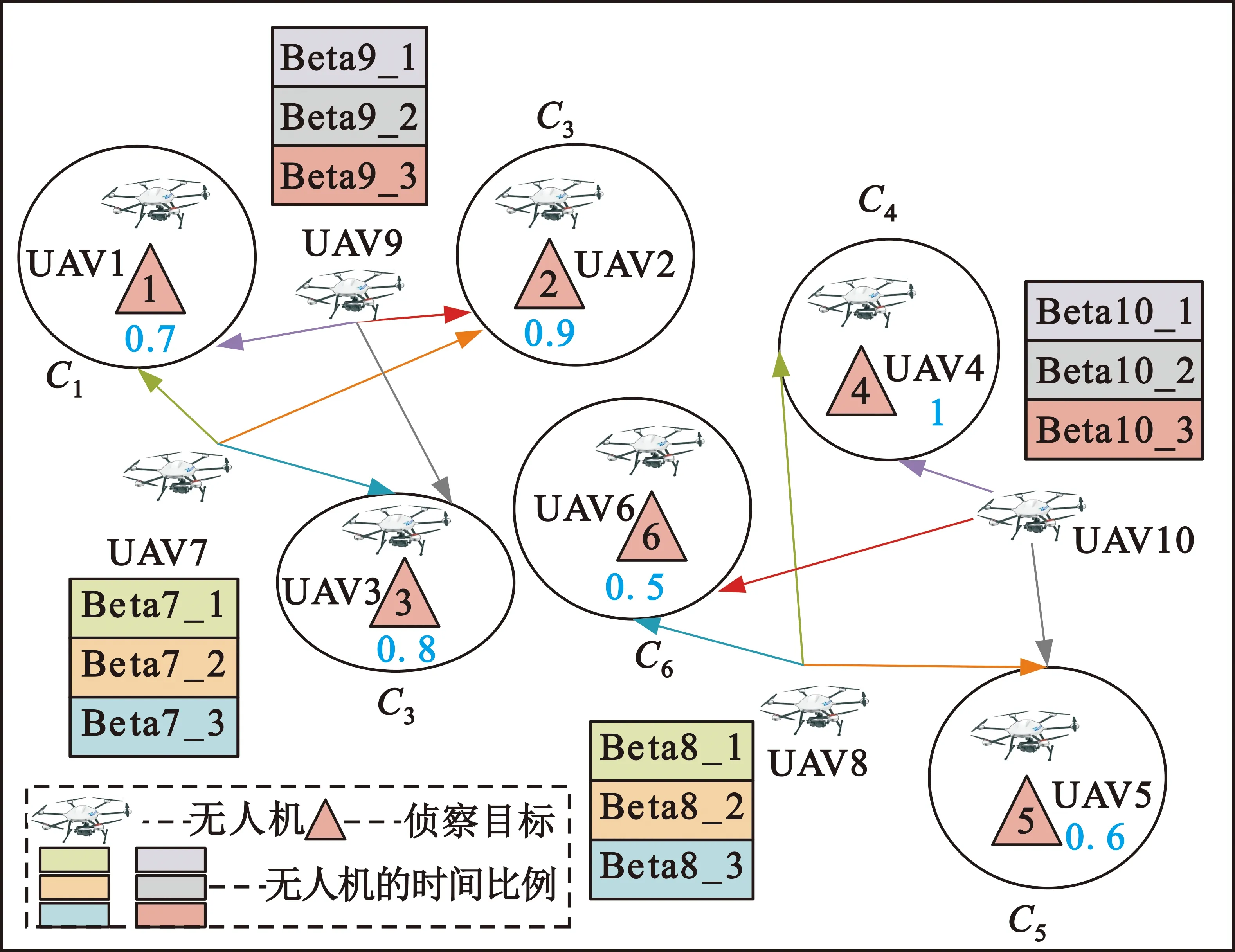
图1 系统模型
无人机在执行侦察任务时,首先需要考虑距离因素。距离侦察目标最近的无人机对该目标进行侦察,不仅满足侦察任务的时效性,而且节省了无人机的飞行成本。忙碌无人机距离侦察任务最近,令其对侦察目标进行全时段侦察。空闲无人机将自己的时间划分成3份进行辅助侦察。

2 重叠联盟博弈模型
2.1 重叠联盟博弈的基本概念
定义1[21]:设联盟参与者的集合为N={1,2,3,…,n},对于任意的C⊆N,称C为N的一个联盟,称Γ={C|C⊆N}为联盟集合。联盟集合Γ中共有2n个元素,C=∅和C=N为两种特殊情况,其中C=N称为大联盟。
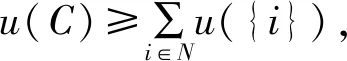
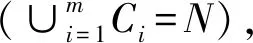
2.2 重叠联盟博弈的效用函数
无人机侦察的识别成功率由S型函数[25]来表示:
(1)
式中:r为无人机的分辨率;T为无人机的侦察时间;a和b为S型函数的参数。当有两架及以上的无人机侦察时,识别成功率为1减去两架及以上的无人机侦察失败的概率。
对一个重叠联盟Ci而言,识别收益等于识别成功率乘以价值函数。价值函数与侦察任务的重要程度成正比,侦察任务越重要价值函数越大。联盟Ci的识别成功率为
(2)

一个重叠联盟Ci的识别代价为联盟内所有无人机拍照侦察时的能量开销,每架无人机能量开销等于侦察时间乘以单位时间的能量开销。联盟Ci的能量消耗为
(3)
式中:Px,Py,Pk分别表示无人机x,y,k单位时间的能量消耗。
一个重叠联盟Ci的效用等于该联盟的收益减去该联盟的代价,效用函数为

(4)
式中:V(i)表示联盟Ci价值函数。联盟Ci内的侦察任务越重要,价值函数就越大。
系统总的效用等于各个联盟效用之和:
(5)
3 重叠联盟形成算法
侦察系统中的无人机为博弈参与者,要求的解是使侦察系统收益增大的一个稳定的联盟结构。首先,对所有的无人机根据距离进行预分配,找出系统中的忙碌无人机和空闲无人机。然后找出空闲无人机的3个潜在辅助联盟,得到所有可能的联盟结构。最后对空闲无人机的时间比例进行优化。
每个空闲无人机通过改变时间分配比例来提升整个系统效用。当所有空闲无人机的时间分配比例都不再改变时,此时便得到一个稳定的重叠联盟结构。改变包括两种情况:转移联盟和退出联盟[26]。以无人机y为例来进行转移联盟和退出联盟的解释说明。
假设无人机y的3个潜在辅助联盟为Ci,Cj和Cm,侦察时间为Ty,时间分配比例为β=[β1,β2,β3],β1为无人机y辅助联盟Ci的时间比例,β2为无人机y辅助联盟Cj的时间比例,β3为无人机y辅助联盟Cm的时间比例。无人机y为了能够使其辅助的联盟获得更高的收益进行一次时间分配比例的改变。
1)转移联盟:当β=[0.2,0.35,0.45]改变为β=[0.4,0.15,0.45]时表示无人机y将时间资源从联盟Cj转移到联盟Ci,此时无人机y侦察联盟Ci,Cj和Cm的时间分别为0.4Ty,0.15Ty和0.45Ty。转移联盟的条件为无人机y将时间资源从联盟Cj转移到联盟Ci后,所辅助的联盟效用之和提升,系统的总效用提升。
2)退出联盟:当β=[0.2,0.35,0.45]改变为β=[0.2,0,0.45]时表示无人机y从联盟Cj中退出,退出之后的时间资源用于辅助其他联盟。退出联盟的条件为无人机y退出联盟Cj后,所辅助的联盟效用之和不降低,系统的总效用提升。
系统中的其他空闲无人机同样进行转移联盟和退出联盟来提升所辅助联盟的收益,进而提升侦察系统收益。每个空闲无人机寻找自己邻近的联盟作为潜在的辅助对象,然后判定是否需要进行转移联盟和退出联盟的操作。在一轮决策中,每个空闲无人机都优化一次自身的时间比例。如果在一轮决策中没有一个空闲无人机需要进行转移联盟和退出联盟的操作,此时收敛到稳定解。重叠联盟博弈均衡求解流程如图2所示。

图2 重叠联盟博弈均衡求解流程
4 仿真分析
考虑N=6,M=10的侦察系统,多无人机协同侦察多目标场景如图3所示,共有6个联盟。uav1~uav6分别为距离6个侦察目标最近的无人机,为忙碌无人机(全时段侦察无人机)。UAV7~UAV9为系统中的空闲无人机,即分配时间比例进行辅助侦察的无人机。
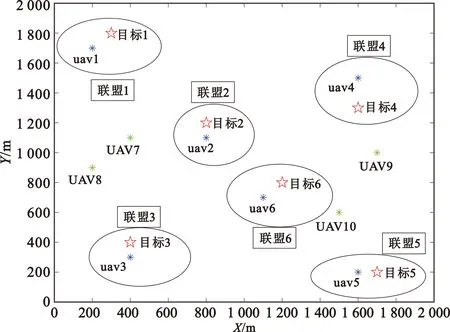
图3 场景预览
侦察目标的参数如表1所示,无人机的基本参数如表2所示,其中侦察时间已进行归一化处理且每架无人机的侦察时间相同。对于空闲无人机来说,首先要找到距离最近的3个联盟作为潜在的辅助对象,然后随机给定一个初始时刻的分配比例,开始进行第一轮决策,每个空闲无人机依次进行决策,所有的空闲无人机全部决策完毕即进入下一轮决策,直到侦察系统的收益不再提升得到稳定的联盟结构为止。初始时刻空闲无人机的分配比例如表3所示。

表1 侦察目标参数

表2 无人机的相关参数

表3 初始时刻空闲无人机的分配比例
根据距离找出距离侦察目标最近的3个联盟作为空闲无人机的潜在辅助联盟,结果如图4所示。由图可知,UAV7能够对联盟1,2,3进行辅助,UAV8能够对联盟1,2,3进行辅助,UAV9能够对联盟4,5,6进行辅助,UAV10能够对联盟4,5,6进行辅助。

图4 空闲无人机潜在辅助联盟
4.1 联盟优化结果
联盟结构达到稳定时,空闲无人机的时间分配比例如图5所示。UAV7~UAV10在联盟结构稳定时的辅助比例均不为0,表示UAV7~UAV10的潜在辅助比例即为实际辅助比例。UAV7辅助联盟1的时间比例为0.48,辅助联盟2的时间比例为0.01,辅助联盟3的时间比例为0.51;UAV8辅助联盟1的时间比例为0.2,辅助联盟2的时间比例为0.59,辅助联盟3的时间比例为0.21;UAV9辅助联盟3的时间比例为0.62,辅助联盟4的时间比例为0.01,辅助联盟5的时间比例为0.37;UAV10辅助联盟3的时间比例为0.01,辅助联盟4的时间比例为0.64,辅助联盟5的时间比例为0.35。

图5 联盟稳定解
稳定时的联盟结构CS*为C1={uav1,UAV7,UAV8},C2={uav2,UAV7,UAV8},C3={uav3,UAV7,UAV8},C4={uav4,UAV9,UAV10},C5={uav5,UAV9,UAV10},C6={uav6,UAV9,UAV10}。
4.2 各联盟识别成功率分析
图6给出了各联盟辅助前后识别成功率对比结果。在没有空闲无人机辅助侦察时,6个联盟的识别成功率均小于0.85,侦察的准确性难以得到有效保障。在空闲无人机加入联盟进行辅助侦察并且达到稳定的联盟结构时,6个联盟的识别成功率均大于0.99,有效保证了无人机侦察的准确性。

图6 各联盟辅助前后识别成功率对比
4.3 联盟总效用分析
多无人机侦察系统总效用(联盟总效用)与迭代次数的关系如图7所示,可见随着迭代次数的增加,联盟的总收益在不断提升。在迭代到第36次时联盟总收益达到收敛状态,继续迭代联盟总收益将不会继续增加。达到收敛状态时,联盟总的效用得到了有效提升。
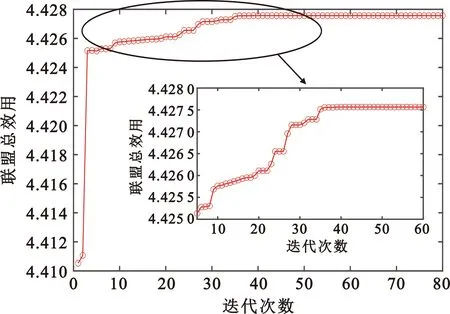
图7 多无人机侦察系统总效用
优化时间比例后的多无人机侦察系统的总效用与未优化时间比例的多无人机侦察系统的总效用对比如图8所示。
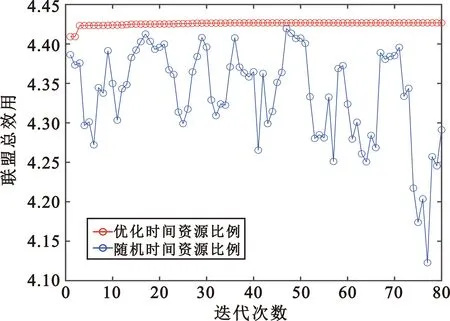
(a)优化时间资源比例
在图8(a)中,优化时间资源比例方法为本文所提方法,随机时间比例方法为每次迭代的时候都随机给定时间资源分配比例。在图8(b)中,固定时间资源比例0为初始时刻空闲无人机的分配比例,固定时间资源比例1,2,3为除初始比例外的3个时间分配比例。UAV7,UAV8,UAV9,UAV10的时间分配比例为β7,β8,β9,β10。固定时间资源比例1为β7=[0.6,0.2,0.2],β8=[0.2,0.5,0.3],β9=[0.3,0.3,0.4],β10=[0.7,0.15,0.15];固定时间资源比例2为β7=[0.4,0.3,0.3],β8=[0.3,0.2,0.5],β9=[0.33,0.33,0.34],β10=[0.25,0.35,0.4];固定时间资源比例3为β7=[0.3,0.4,0.3],β8=[0.33,0.33,0.34],β9=[0.4,0.3,0.3],β10=[0.33,0.34,0.33]。
由图9可知,本文所采用的优化时间资源比例的方法要优于随机时间资源比例方法。由图10可知,与固定时间资源比例相比,优化时间资源比例更能够提高联盟的总效用。 综上所述,基于重叠联盟博弈的无人机侦察时间资源分配优化方法不仅能够提高侦察系统的总效用,而且无人机的时间资源得到了高效的利用。
5 结 论
本文考虑利用多无人机对价值异构的多目标进行协同侦察时的时间资源分配问题。首先,根据距离找出侦察系统中的忙碌无人机和空闲无人机。然后通过构建重叠联盟博弈模型,优化侦察系统中空闲无人机的时间资源分配比例。在重叠联盟博弈模型达到稳定状态时,得到了所有无人机的时间资源分配方案。最后,对整个侦察系统收益进行了仿真验证。仿真结果表明,所提出的多无人机的时间资源分配方案使得整个系统的侦察收益得到了有效提升。
