基于模糊PID融合的特种起重机伸缩臂自动控制

马 珂,何培彬

(河南省特种设备安全检测研究院商丘分院,河南 商丘 476000)

0 引言

运输机械应用最为广泛的就是起重机[1],其主要应用在港口码头、建筑运输等方面。在当今工业化水平不断提升的情况下,起重机的伸缩臂[2]发挥着重要功能,而伸缩臂的好坏影响着起重机的综合性能。由于起重机伸缩臂工作任务量的不断提升,导致伸缩臂的机构受到磨损,进而导致伸缩臂的控制精度下降,大大降低了起重机伸缩臂的应用效果。因此,为了有效避免这种问题的发生,需要对特种起重机机械臂自动控制方法进行研究。

石怀涛等[3]提出基于能量分析的桥式起重机防摆控制方法。由于一般情况下起动机的抑制效果及控制效果较差,所以设计了一个起重机控制器,并构建起重机储能函数,通过设计的控制器对起重机的闭环反馈系统实行控制,进而提升起重机吊运效率,但该方法设计的控制器不够完善,导致存在控制效果差等问题。曹传剑等[4]提出基于自适应滑模控制的随车起重机控制特性分析方法。优先对起重机的控制系统性能及数学模型进行详细分析,根据该原理设计控制器,利用该控制器对起重机实行控制,使起重机达到稳定的目的,但该方法的分析结果存在误差,存在伸缩臂位移响应与期望结果相差较大的问题。李锐等[5]提出基于改进RBF神经网络PID控制的液压起重机节能方法。该方法根据起重机伸缩臂平面建立了平面简图,通过设立起重机平衡阀推导出起重机动力学方程式,采用RBF神经网络建立了控制器,并利用该控制器对起重机实行控制,从而实现降低起重机液压泵输出功率的目的,完成起重机的整体控制,但该方法推导的方程式有所欠缺,存在控制精度较差的问题。

为了解决上述方法中存在的问题,本文提出基于模糊PID融合的特种起重机伸缩臂自动控制方法。

1 特种起重机伸缩臂受力分析

1.1 特种起重机伸缩臂结构分析

伸缩臂在起重机中占据着关键地位,它是整个起重机的核心,伸缩臂的性能参数变化会对起重机的使用效果造成一定影响。在特种起重机中,伸缩臂是主要承重部件,其承受度要达到15%～20%。由于伸缩臂的安装机构在伸缩臂的内部,所以伸缩臂的结构、重量会对起重性能造成影响。

a.起重能力。起重机的起重能力往往与重量有关,但不限于自身重量,还包含起重机伸缩臂中的吊钩或吊具。吊钩在伸缩臂中会随着伸缩臂的变化而不断变化,当伸缩臂在运行期间角度发生改变时,起重机的起重量也会出现变动。由此可见,伸缩臂的结构强度与起重机的稳定性能影响着起重机的起重能力。

b.起重高度及幅度。起重机伸缩臂在吊取装置时,伸缩臂吊钩的最高点与最低点的距离就是需要起升的高度,而中心线之间的垂直距离就是幅度。起重高度和幅度对起重机伸缩臂的工作效果起到决定性影响,因而需要判定好起重机伸缩臂的位置参数。

c.力矩。伸缩臂工作期间的起重力矩主要体现在伸缩臂的额定起重量与工作运行幅度的乘积,是伸缩臂关键技术主要构成部分。

1.2 特种起重机伸缩臂受力分析

获取特种起重机伸缩臂的变幅平面,根据变幅平面建立伸缩臂坐标系,以此对伸缩臂受力实行分析[6]。

a.伸缩臂垂直载荷。特种起重机伸缩臂的垂直载荷为

(1)

Q为垂直载荷[7];φ2为动载荷系数;Q0为质量大小,主要包含伸缩臂的吊钩、吊具等;φ1为冲击系数;C0为伸缩臂自重。

b.起重机伸缩臂起升时的拉力。起重机伸缩臂在起升过程中的钢丝绳拉力为

S=(φ2+Q0)/mη

(2)

S为钢丝绳的拉力;m为起升时的倍率;η为实际起升滑轮效率。

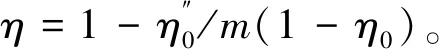
在伸缩臂变幅平面中,额外载荷为

(3)

N为轴向力;Tz为横向力;β1为线角度大小;u为伸缩臂轴线在同一水平面中的角度。

由于伸缩臂的垂直载荷Q与钢丝绳的拉力会对伸缩臂造成影响,所以就会自动形成伸缩臂额外力矩,表示为

ML=φ2+Q0+e1sinu-Se2+cosβ1

(4)

ML为额外力矩;e1为实际偏心距;e2为理想偏心距。

2 基于模糊PID融合的伸缩臂控制

2.1 建立伸缩臂数学模型

通过对起重机的结构及变幅平面的详细分析,以此为基础建立以伸缩臂变频器、交流电机、减速器及检测装置为主的起重机伸缩臂数学模型,推导出特种起重机伸缩臂的传递函数。

a.伸缩臂变频器。伸缩臂系统中变频器是不可或缺的一部分,而变频器的输入电压为ue,与其相对应的电压频率就设定为f,即f=50 Hz。因此变频器与电压的比例关系表示为:f1=K1+uc。其中,K1为电压频率的变换系数。

当起重机伸缩臂系统中的交流异步电机处于稳定状态时,电压与电动势之间的关系可表示为

U=Et+ItZt=

j2π+f1+Lh+Ih+RtIt+j2πfLtIt

(5)

U为电压;f1为电压频率;Lh为定转子互感;Lt为定子自感;Ih为励磁电流;It为定子相电流;Rt为电阻;j为频率系数;Et为电动势;Zt为转换系数。

特种起重机伸缩臂的定子电势较小时,会出现漏阻抗压降问题,对伸缩臂的控制效果造成一定的不利影响,因而需要降低漏阻抗压降带来的影响。设定补偿电压为U0,则定子电压U1与变频器之间的关系f即可表示为

U1=(220-U0/50)f+U0

(6)

对伸缩臂低频定子补偿电压忽略不计时,可定义为

U1=4.5f=23uc

(7)

其中,f1=K1+uc。式(6)、式(7)即为变频器的数学模型表达式。

b.起重机伸缩臂交流异步电机。起重机伸缩臂交流异步电机是一种多变量系统,伸缩臂在机械传动过程中,电机中的电磁会发出非常短暂的变化,此时的电磁转矩为

Te=3np+(U1/ω1)2+

(8)

np为极对数;Te为电磁转矩;ω1为角速度;Rs为定子电阻;Rr为转子电阻;s为转差率。

电机的转动速度[8]与电机的额定工作状态保持一致,电机的转差率就会减小,因此,将转差率s=(n1-n)/n1代入到电磁转矩中,其中,n为实际转速,则存在下述表达式,即

(9)

对式(9)进行转换,并忽略定子补偿电压,取得伸缩臂电机的电磁转矩为

(10)

基于恒转矩负载,获取伸缩臂电机运动方程表达式为Te=TL+(Y/np)+(dω/dt)。其中,TL为负载转矩,Y为转动惯量,ω为电机转动速度。将上述表达式代入到式(10)中,获取拉氏变换后的伸缩臂交流异步电机数学模型为

(11)

Kn(n=1,2,3)为伸缩臂电机的电压频率转换系数,且Kn随着n=1,2,3的不同,其取值范围均不相同。

c.起重机伸缩臂减速器。减速器在起重机伸缩臂工作过程中起到重要作用,主要连接电机转轴与起重机伸缩臂的转轴,其数学模型定义式为:i=n/n1。其中,i为减速器电流,n1为车轮转速。

d.起重机伸缩臂检测装置。将位移传感器作为起重机伸缩臂的运动检测装置,并把起重机伸缩臂的位置信号用作检测装置的输入信号,而电压模拟量信号用作输出信号,此时的起重机伸缩臂检测装置数学模型可以表示为:Uf=Kf+A。其中,Kf为传感器的增益效果,Uf为反馈电压,A为起重机伸缩臂位移。

结合上述分析,构建起重机伸缩臂的整体数学模型为

(12)

r为起重机的车轮半径。

根据取得的起重机伸缩臂数学模型表达式,对其进行推导获得传递函数。

2.2 模糊PID融合控制器

模糊PID控制器[9-10]是一种能够对系统产生的稳态误差实行抑制,从而达到最佳控制效果的控制器。因而将其与上述获取的特种起重机伸缩臂数学模型的传递函数相结合,以此实现特种起重机伸缩臂自动控制。

将传统的PID控制器与模糊控制器相结合,共分成2种结构,其主要原理如图1所示。

图1 模糊PID融合的串并联控制原理

图1中,A为电流,AC为交流电,k为模态控制参数,Y为模糊PID控制参数。由图1可知,模糊PID融合的控制结构有串联和并联2种。当模糊PID串联控制时,需要对伸缩臂在暂态过程中的设定值进行跟踪,而此时PID的参数会随之变化。当起重机伸缩臂处于不同状态时,PID的控制作用均不相同,即可利用A、AC对伸缩臂的比例增益参数KP、积分增益参数KI和微分增益参数KD实行调整,从而优化控制效果。

模糊PID融合控制并联结构时,共有PID和模糊2种控制模态。由于起重机伸缩臂存在稳态误差,所以当模态控制参数k小于设定的阈值时,就需要对控制器实行转换,利用双模控制器达到最终伸缩臂控制效果。使其具备控制响应速度快、稳态精度高和控制效果优的特点。

综上所述,本文主要根据特种起重机伸缩臂的结构分析及受力分析,取得起重机伸缩臂系统的数学模型,从中推导出传递函数后,将其与模糊PID融合相结合,完成特种起重机伸缩臂自动控制。

3 实验与分析

为了验证基于模糊PID融合的特种起重机伸缩臂自动控制方法的整体有效性,需要对该方法实行实验对比测试。采用基于模糊PID融合的特种起重机伸缩臂自动控制方法(本文方法)、基于自适应滑模控制的随车起重机控制特性分析方法(方法1)和基于改进RBF神经网络PID控制的液压起重机节能仿真(方法2)进行实验测试。

a.通过构建的实验平台,获取起重机伸缩臂从变幅运动到水平面平行位置时的位移,同时根据期望规律对起重机伸缩臂实行伸缩运动,以此利用位移传感器获取伸缩臂的变化。为了验证3种方法的整体控制效果,设定2种工况条件,采用本文方法、方法1和方法2开展伸缩臂位移测试,将其与期望位移对比,从中检验出3种方法的控制效果。具体测试结果如图2所示。

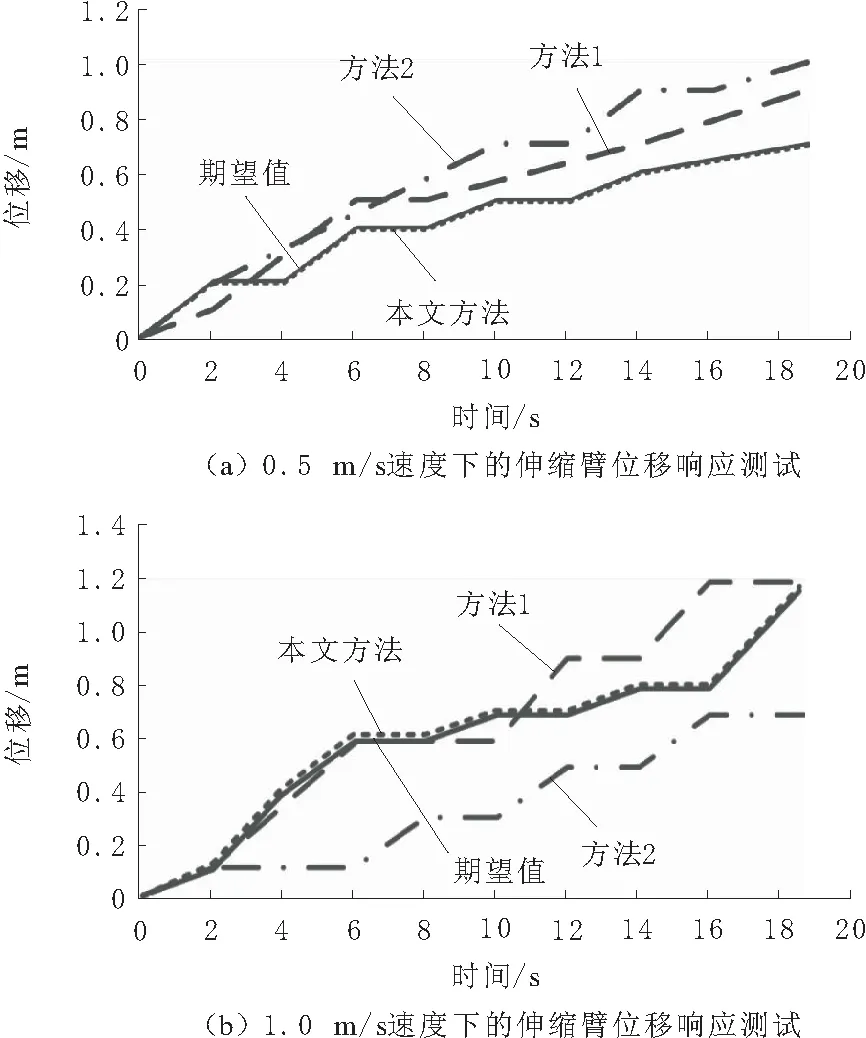
图2 不同速度下的伸缩臂位移响应测试

由图2可知,即使是在不同的工况条件下,本文方法与期望值之间几乎没有误差,表明了该方法的伸缩臂位移响应控制精度高。在时间不断增加情况下,方法1和方法2不论是从运动轨迹还是位移量来说,都与期望值存在偏差,因而可以判定方法1和方法2的伸缩臂控制效果较差。

b.起重机伸缩臂在作业期间需要根据作业路径及时对伸缩臂的末端姿态实行调整,再展开运作。末端姿态主要指的是末端执行器从原位置到指定位置的距离。因而针对伸缩臂的末端姿态位置与期望位置开展详细对比,以此验证3种方法的控制效果,测试结果如图3所示。

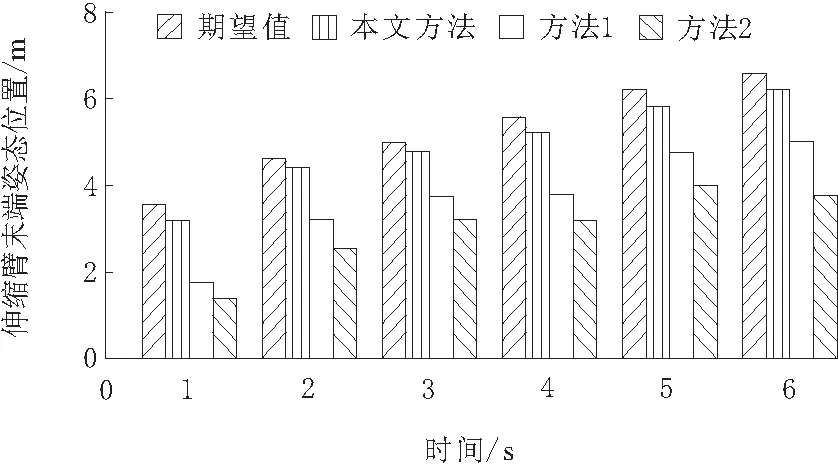
图3 伸缩臂末端姿态位置与期望位置对比测试

由图3可知,随着时间增加,3种方法测试出的伸缩臂末端姿态位置均与期望结果存在误差。但经整体对比,本文方法的误差较小,更接近于期望值。而方法2的误差最大,与期望位置距离最远。由此可以断定本文方法的控制结果最优,这主要是因为本文方法对起重机伸缩臂实行了受力分析,为后续伸缩臂的自动控制奠定了详细的信息基础,因而增强了控制精度,提升了整体控制效果。

以实验b的设定条件为主,在不同时间下的伸缩臂末端力与期望力之间的控制曲线进行对比,具体如图4所示。

图4 伸缩臂末端力与期望力测试

由图4可知,与方法1和方法2相比,本文方法的伸缩臂末端力运动轨迹与期望值基本一致,说明本文方法的伸缩臂末端力与期望值的偏差小,精度高。

4 结束语

伸缩臂是起重机的核心,伸缩臂的性能会对起重机的运行效果造成影响,针对特种起重机伸缩臂自动控制存在的问题,提出基于模糊PID融合的特种起重机伸缩臂自动控制方法。分析了伸缩臂的整体结构及受力情况,根据分析结果构建伸缩臂数学模型,并从中推导出伸缩臂传递函数,将其与设计的模糊PID融合控制器相结合,实现伸缩臂自动控制,并通过实验验证了该方法的有效性。该方法在伸缩臂自动控制方法中发挥着重要作用,在今后机械控制领域中有着较好的发展前景。