下弦与撑杆新构型张弦梁结构的抗连续倒塌性能

蒋友宝 张梦华 周浩

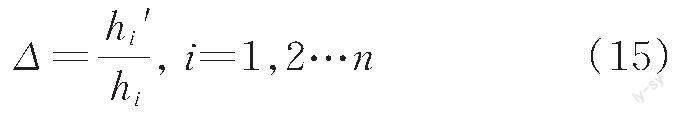
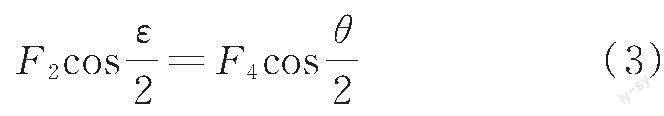
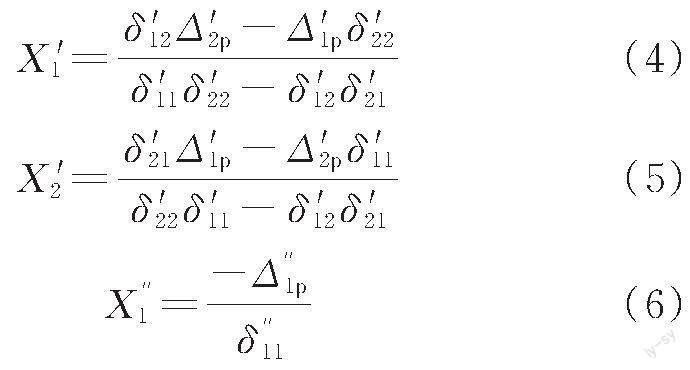
摘要：由于传统张弦梁结构冗余度较低，下弦预拉索遭受意外作用断裂时易导致结构发生连续倒塌。通过改进传统张弦梁撑杆、下弦等杆件构型与连接形式，提出一种新型张弦梁结构。基于ANSYS/LS-DYNA程序平台，采用考虑初始状态的等效荷载瞬时卸载法，对具有不同撑杆交叉角度和交叉撑杆组数量的多个新型张弦梁结构模型进行抗连续倒塌分析。结果表明：合理设计后，任一段下弦失效时，交叉撑杆将代替失效处下弦为结构提供备用传力路径，新型张弦梁结构不会发生连续倒塌，但会导致下部撑杆内力骤增，下部撑杆设计需预留较大承载余量；撑杆交叉节点越靠近下弦，剩余结构空腹桁架作用越明显，承载能力越好；交叉撑杆组数越多，结构冗余度越高，新型张弦梁结构抗连续倒塌性能越优。

关键词：张弦梁结构；连续倒塌；动力分析；撑杆；下弦

中图分类号：TU318     文献标志码：A     文章编号：2096-6717（2023）06-0012-09

Progressive collapse resistance of beam string structure based on a new configuration of bottom chord and strut

JIANG Youbao， ZHANG Menghua， ZHOU Hao

（Hunan Provincial Key Laboratory of Green Construction and Maintenance of Bridges and Buildings， Changsha University of Science and Technology， Changsha 410114， P. R. China）

Abstract： Due to the low redundancy of the traditional beam string structure， it is easy to cause a continuous collapse of a structure when the lower string prestay cable is broken by accident. A new type of beam string structure is proposed by improving the traditional tensioned beam spars， lower chords and the connection forms among members. Based on ANSYS/LS-DYNA program platform， some new beam string structure models with different spars crossover angles and spars numbers are analyzed for continuous collapse resistance by using the instantaneous unloading method of the equivalent load in the initial state. The results show that after reasonable design， the cross strut will replace the lower chord at the failure to provide a spare force transmission path for the structure when any section of the lower chord fails，and the new beam string structure will not progressive collapse， but the lower spar internal force will increase suddenly， the large bearing allowance shall be reserved for the design of the lower brace. And also show that the closer the brace cross node is to the bottom chord， the more obvious the effect of the vierendeel truss of the remaining structure and the better the load carrying capacity. The more cross brace groups， the higher the structural redundancy， and the better the progressive collapse resistance of the new beam string structure.

Keywords： beam string structure； progressive collapse； dynamic analysis； strut； lower chord

近30年來，大跨度空间结构发展迅速，被广泛应用于体育馆、机场、火车站等人流量较大的场所，然而，其在极端或意外荷载作用下往往易发生连续倒塌，造成极其恶劣的影响[1]。1978年，由于暴风雪持续作用，哈特福德体育馆屋盖网架发生整体垮塌[2]。由于部分焊缝存在严重质量缺陷，个别杆件接料不够规范，加之遇到骤冷天气，2011年鄂尔多斯那达慕大会主会场钢结构罩棚出现较大伸缩而发生塌落。因此，大跨空间结构倒塌问题引起了学者们的广泛关注[3-5]。

目前，作为一种应用广泛的大跨空间结构，张弦结构抗连续倒塌性能研究已有一定进展。Zhao等[6]分析了张弦梁结构的静力性能与动力特性，并提出了张弦梁结构在抗连续倒塌分析方向的关注点。胡帅领[7]对张弦结构的连续倒塌规律进行了仿真分析，得出了局部破坏和强震作用下张弦结构的倒塌规律，并提出了适用于设计的相应措施。蔡建国等[8]以张弦结构为研究对象，得到了撑杆失效对结构连续倒塌性能的影响规律。曾滨等[9]提出了一种增设备用索方案，以提高张弦梁结构冗余度。Zhou等[10]考虑了随机荷载比对张弦梁结构极限承载力的影响，提出了两种改进方法，以提高张弦梁结构的承载及抗倒塌性能。余佳亮等[11]对无站台柱张弦桁架雨棚结构进行了研究，基于结构动力响应分析，提出了双索设计思想，以提高结构抗连续倒塌能力。

针对传统张弦梁冗余度较低的特点，笔者团队之前提出了一种改进撑杆构型的新型张弦梁结构，数值分析结果表明，其抗连续倒塌性能较好[12]。在此基础上，笔者通过进一步改进结构下弦连接形式，提出一种下弦与撑杆新构型的张弦梁结构体系，并基于ANSYS/LS-DYNA程序平台对新型张弦梁的抗连续倒塌性能进行参数分析。

1 下弦与撑杆新构型的张弦梁结构

1.1 结构组成及倒塌受力特点

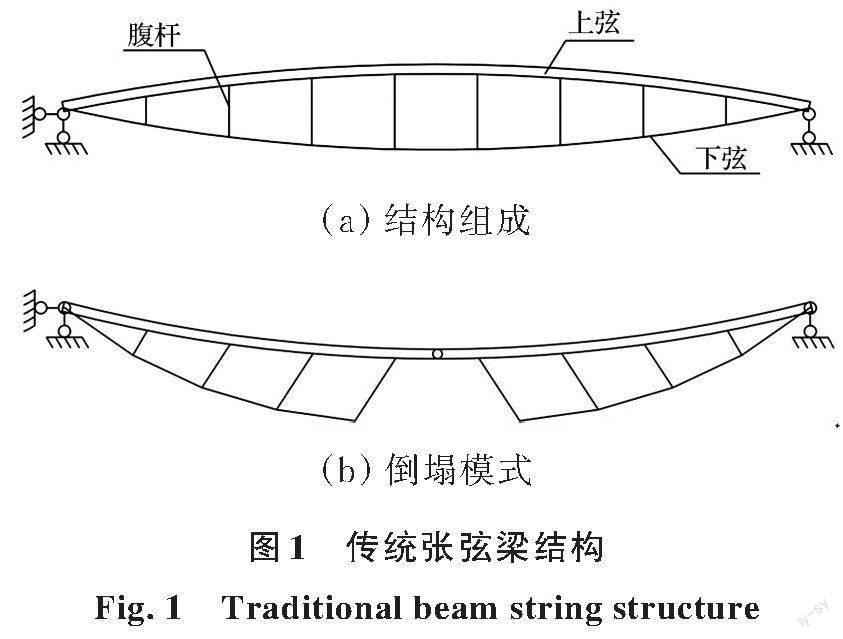
传统张弦梁结构常为单一竖向撑杆连接上弦刚性构件与下弦柔性拉索后形成的一种自平衡结构体系，如图1（a）所示。基于上述结构组成方式，若传统张弦梁受到意外荷载作用导致下弦任一截面拉索失效时，整段拉索会迅速失效，继而带动竖向撑杆转动，上弦失去支撑后跨中挠度急剧增加，上弦刚性杆件被压溃，致使结构发生倒塌，倒塌模式如图1（b）所示。

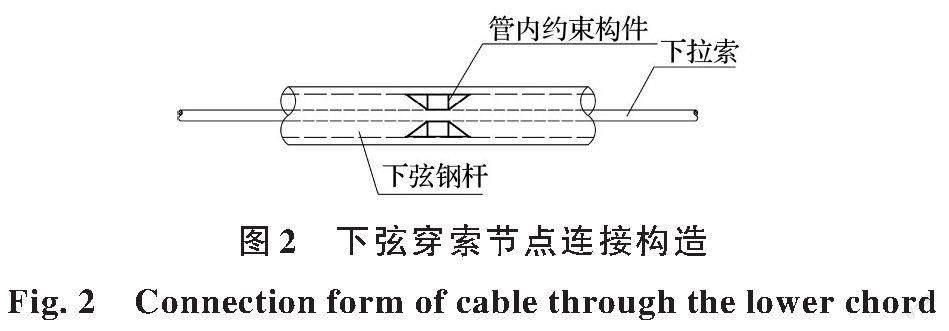
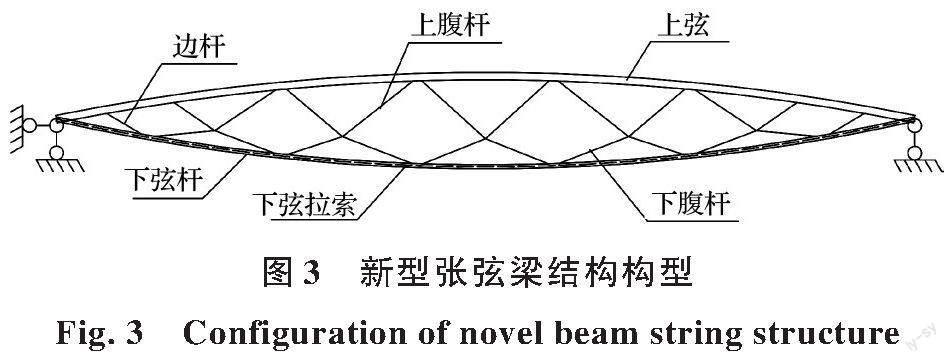
为解决传统张弦梁冗余度低的问题，改进了传统的撑杆、下弦等杆件构型及连接方式。撑杆采用一种新型交叉撑杆代替单一竖向撑杆；下弦采用高强钢管内穿柔性拉索组合代替单一柔性拉索，下弦杆与内穿拉索的连接构造如图2所示（该构造已在成都“新世纪”国际会议会展中心等钢结构工程中应用）[13]；撑杆、撑杆与上弦杆、撑杆与下弦杆之间选用焊接连接代替传统张弦梁铰接连接。该新型张弦梁结构如图3所示。

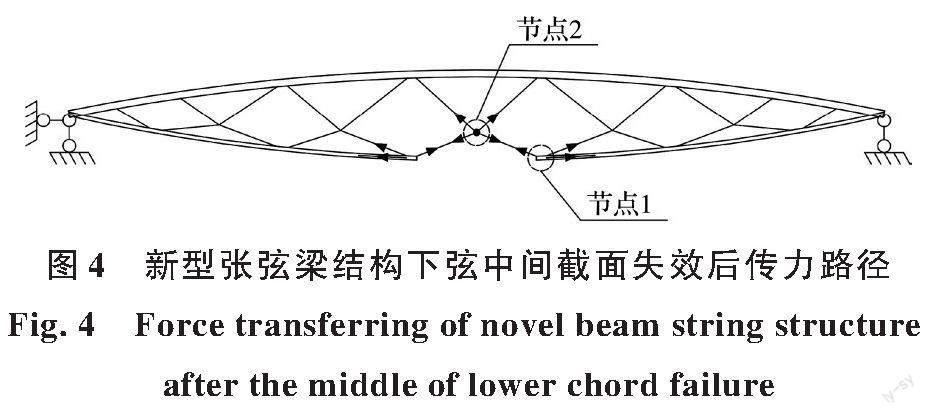
对于新型张弦梁结构，若意外荷载作用导致下弦任一截面失效，下弦内穿拉索将快速丧失应变能，对结构产生较大冲击，但由于各杆件之间的连接方式为焊接，连接节点处可达到新的受力平衡，削弱下弦失效对结构的冲击作用。新型张弦梁跨中下弦截面失效后结构传力形式如图4所示。

1.2 结构抗连续倒塌性能的改进原理

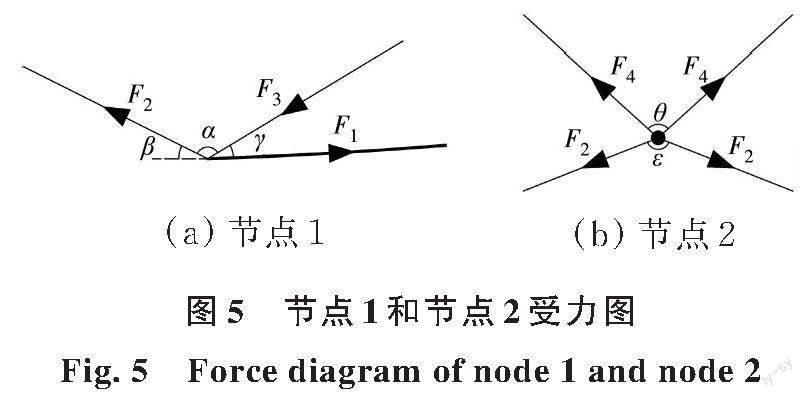
结合新型张弦梁结构跨中下弦失效后的传力路径发现，在某一下弦失效后，节点1和节点2可重新达到受力平衡，如图5所示。其中节点1在下弦杆切线与法线方向的受力平衡方程满足式（1）、式（2）。

F2 cos β + F3 cos γ = F1 （1）

F2 sin β = F3 sin γ （2）

式中：F1為节点1右侧下弦杆轴力；F2、F3分别为节点1左右两侧下部撑杆轴力。

下部撑杆通过节点2将内力F2传给上部撑杆，节点2沿竖直方向的受力满足式（3）所示平衡方程。

式中：由于节点2位于跨中，其左右两侧杆件对称布置，因此将两侧上腹杆内力均设为F4，两侧下腹杆内力均设为F2。

分析式（1）～式（3）可知，在F1不变的情况下，增大角度α，可使β与γ减小，下部撑杆对应的内力值F2和F3更小，承载余量更高。同时，若新型张弦梁结构交叉撑杆与上弦杆和下弦杆连接位置确定，角度α增大，则ε增大、θ减小，上部撑杆对应的截面内力值F4更小，传力路径得到进一步优化。

1.3 结构模型

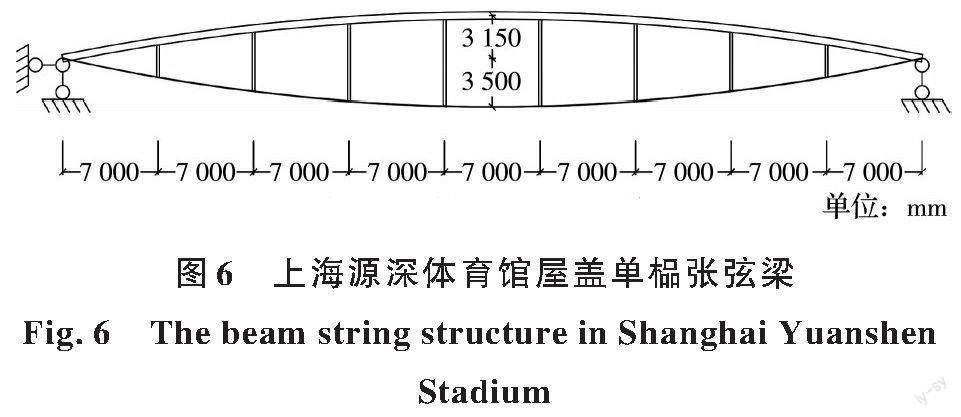
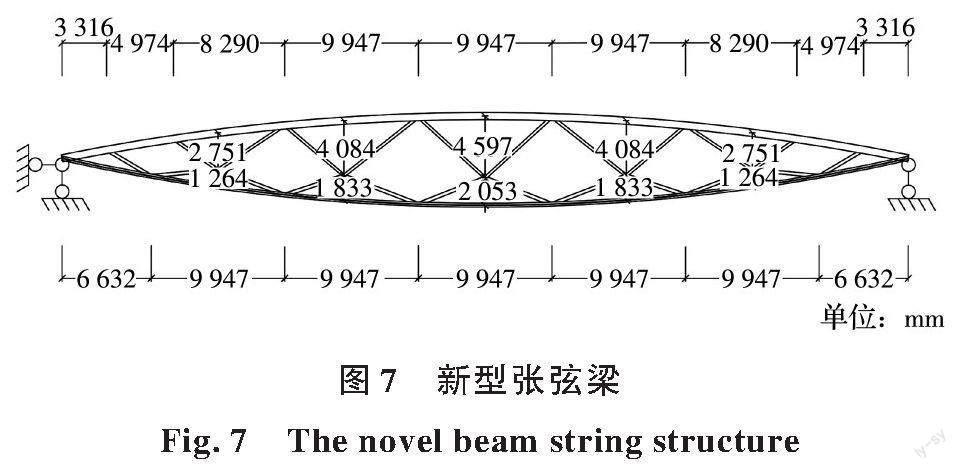
上海源深体育馆屋盖为8榀平行布置、跨度为63 m的预应力张弦梁结构，各榀间距为9 m，相邻两榀之间采用连梁、檩条和斜撑连接[14]。选取该屋盖结构中单榀张弦梁为传统张弦梁结构研究对象，如图6所示，设计参数如表1所示（全景示意图详见文献[14]）。在该传统张弦梁的基础上进行改进，得到基于下弦与撑杆新构型的张弦梁结构，见图7，其设计参数见表2。分析模型为单榀张弦梁结构，不考虑其与周边空间结构的碰撞。

1.4 新型张弦梁结构下弦断裂前后静力分析

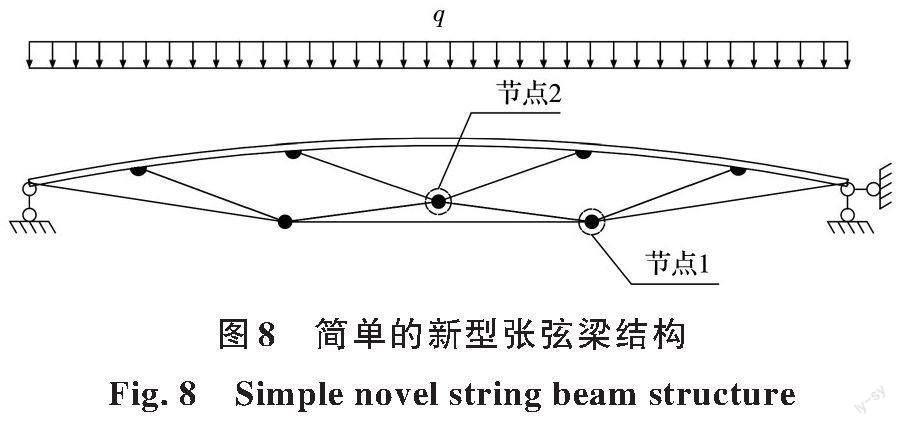
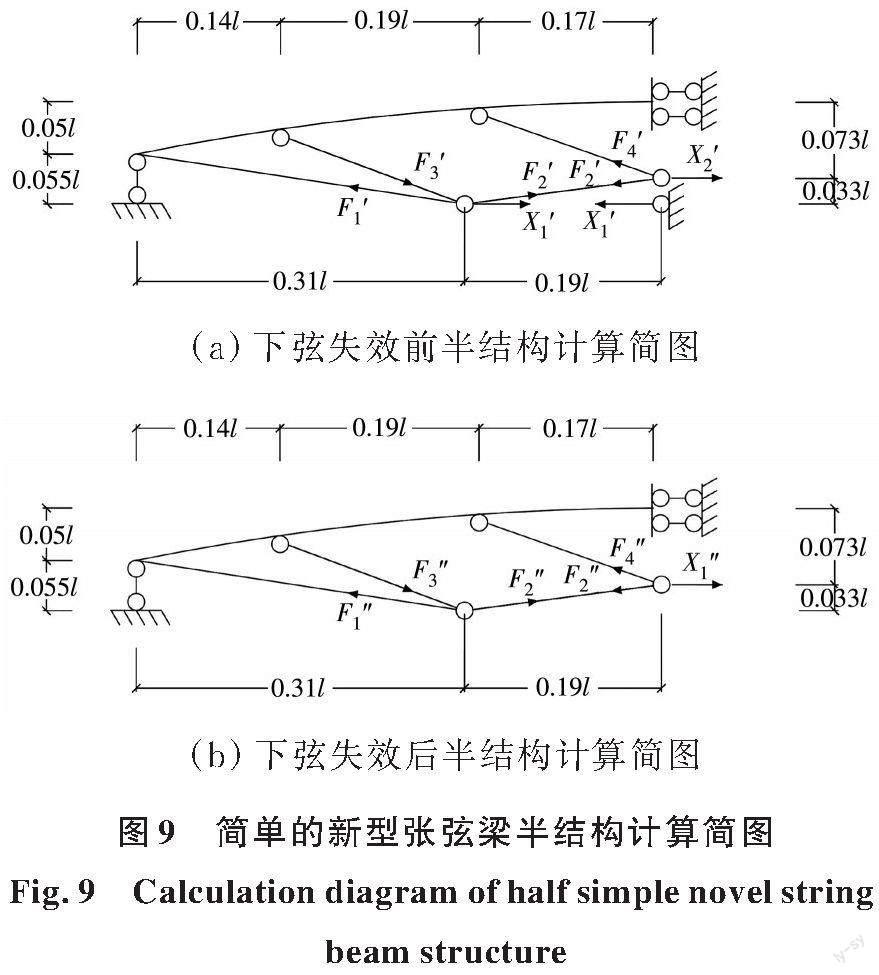
以一简单的新型张弦梁结构模型为例，见图8，分析下弦断裂前后各杆件内力变化。结构考虑全跨均布荷载作用，假定钢材弹性模量为E，上弦、下弦、上撑杆和下撑杆的面积和惯性矩分别为A1、A2、A3、A4和I1、I2、I3、I4，撑杆所受弯矩影响较小，可忽略。采用力法对结构模型进行理论求解，取半结构分析，下弦失效前后结构计算简图见图9。

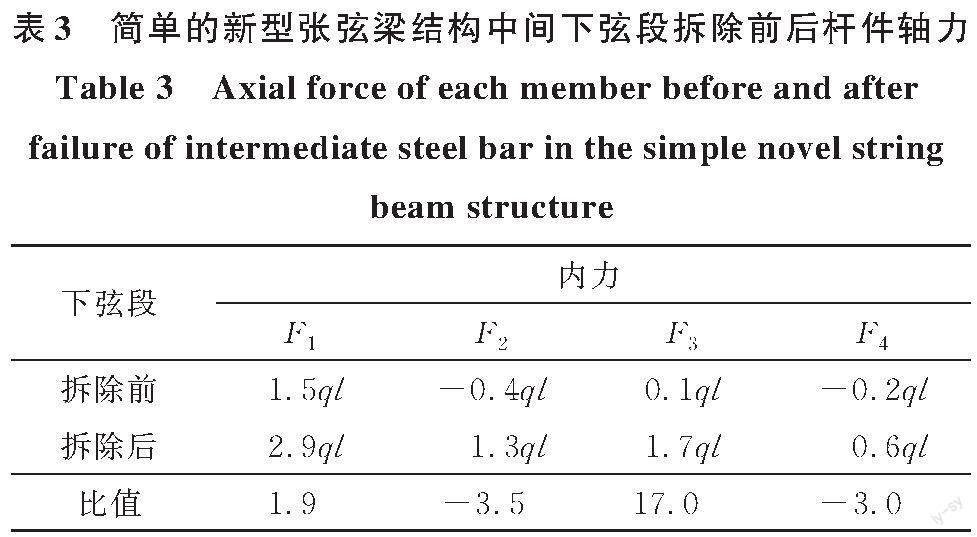
由力法基本方程可解下弦失效前后内力X1'、X2'与X ''1，见式（4）～式（13）。结合表2 数据，求得下弦失效前后各杆件内力，结果见表3。

其中

式中：δii （ i = 1，2…n ） 为基本体系由Xi=1 产生的Xi方向上的位移；δi（j j=1，2…n）为基本体系 Xj=1产生的Xi方向上的位移；Δip 为基本体系由荷载产生的Xi方向上的位移;l 为结构跨度。

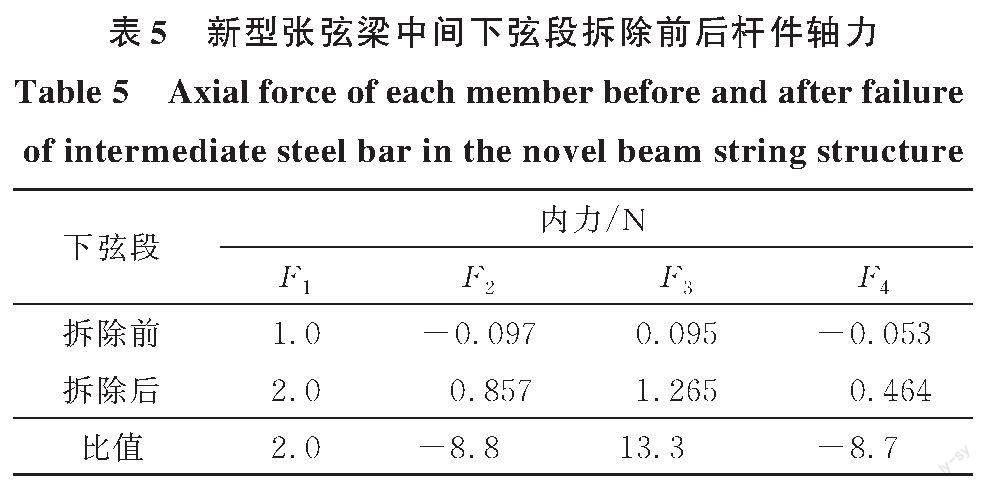
由表3可知，下弦失效后，简化结构各杆件内力均会增大，其中边撑杆的内力增长幅度最大，为下弦失效前内力的17倍；下撑杆与上撑杆的内力增长幅度相似，但下撑杆内力值较上撑杆更大，因此下撑杆与边撑杆需设计较大的截面面积。若完全采取1.3节中新型张弦梁结构形式及设计参数，节点1和节点2各角度大小见表4。考虑全跨均布荷载作用，假定下弦失效前下弦杆承受单位力1 N，下弦失效后，结合简化结构分析及有限元静力分析结果，取同等荷载作用下剩余结构的下弦杆内力值为2 N。结合式（1）～式（3）可计算出下弦截面失效前后杆件内力，结果见表5。

分析表5发现，当不考虑杆件拆除引发的动力效应时，跨中下弦失效后下腹杆内力值急剧增大，最大可增加至原来的13.3倍；若杆件设计安全余量不大，则易由于内力急剧增加而导致其失效，相对于下部撑杆，上部撑杆的内力值较小。因此，结合表3与表5的数据分析结果，为保证结构的抗连续倒塌能力，需要在设计时将下部撑杆及边撑杆的截面加大，以提供足够的承载余量。

综上所述，因受到意外荷载作用导致新型张弦梁跨中下弦断裂失效后，交叉撑杆与下弦钢管的组合形式可为结构提供一种备用受力路径。若位于备用路径上的撑杆设计合理，结构即可通过节点传力达到新的受力平衡，保证在下弦任一截面失效后不会发生连续性倒塌。新型张弦梁结构可提高传统张弦梁结构的冗余度，同时，下弦管内穿索可有效减小下弦钢管的截面面积，对比现有传统张弦梁结构及管桁架结构，该结构受力表现更优异。

2 新型张弦梁抗连续倒塌性能分析

2.1 结构抗连续倒塌性能有限元分析

结构失效准则用于判断结构整体是否发生连续倒塌。对于张弦梁结构，采用变形准则作为判别结构倒塌的依据，即当结构变形不满足式（14）时，认为结构失效倒塌[15]。

式中： [ f ]为结构变形限值；L 为结构跨度。

钱凯等[16]采用ANSYS/LS-DYNA程序对不同结构进行了抗连续倒塌模拟分析，结果表明，该程序具有较高的分析精度。参考该建模思路，基于ANSYS/LS-DYNA程序，采用变换荷载路径法中的非线性动力计算方法进行模拟分析。有限元模型中，上弦杆、撑杆及下弦杆均采用BEAM 161梁单元模拟，其材料本构采用双线性随动强化模型* MAT_PLASTIC_KINEMATYIC；拉索单元采用LINK167，材料本构采用*MAT_CABLE_ DISCRETE_BEAM[17]。传统张弦梁撑杆与上下弦采用自由度释放的方式铰接，而新型张弦梁下弦杆内穿柔性拉索，采取耦合下弦杆与下弦拉索节点竖向自由度的方式连接[18]。

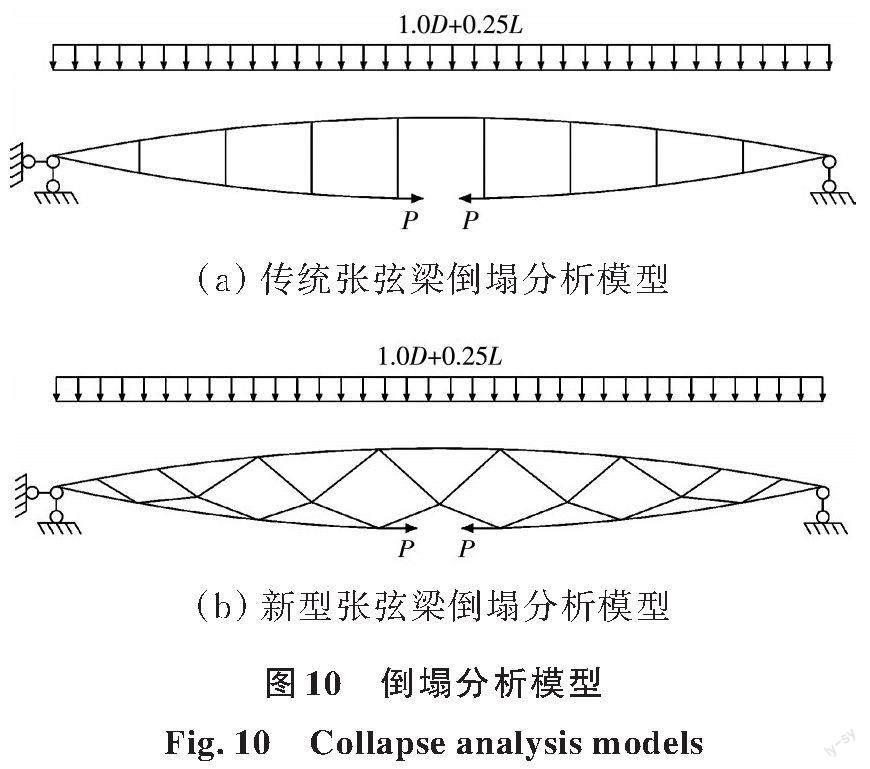
建筑结构抗连续倒塌设计可采用概念设计、拉结构件法、拆除构件法和局部加强法[19]。在张弦梁结构抗连续倒塌有限元分析中，由于对拉索施加了初始预应力，结构将产生初始变形，因此选用拆除构件法中考虑初始状态的等效荷载瞬时卸载法[20]对下弦拉索和下弦杆的失效进行模拟。首先对完整结构进行静力分析，提取拟拆除构件在完整结构倒塌工况下的内力P；然后移除该构件，对剩余结构进行模态分析，提取前两阶竖向自振周期计算剩余结构阻尼；进而将内力P作为等效荷载反作用在剩余结构上，如图10所示。通过Cowper-Symonds准则考虑材料应变率对屈服应力的影响[21]；失效应变εf取值为0.025[22]；结构阻尼按Rayleigh阻尼考虑[23]，取值为0.02。动力分析时，等效荷载取值采用D（恒载）+0.25L（活载）组合工况，并以节点力的形式作用于上弦。

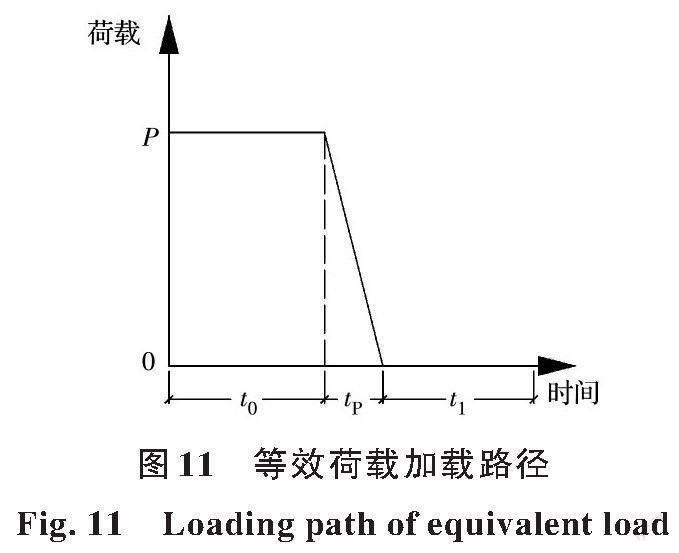
结构在拆除失效构件前后共经历3个阶段，如图11所示。t0为初始持荷阶段，即完整结构在原静力荷载及等效荷载P作用下发生强迫振动直至稳定的时间，通过计算剩余结构自振周期T确定，取t0=25 s；tP为失效构件移除阶段，结合美国GSA规范[24]要求，失效构件移除时间tP应小于自振周期T的1/10，对于下弦杆与下弦索失效，取tP=0.003 75 s[25]；t1为剩余结构在阻尼影响下振幅逐渐减小直至完全稳定的阶段，取t1=25 s。

2.2 结果分析与讨论

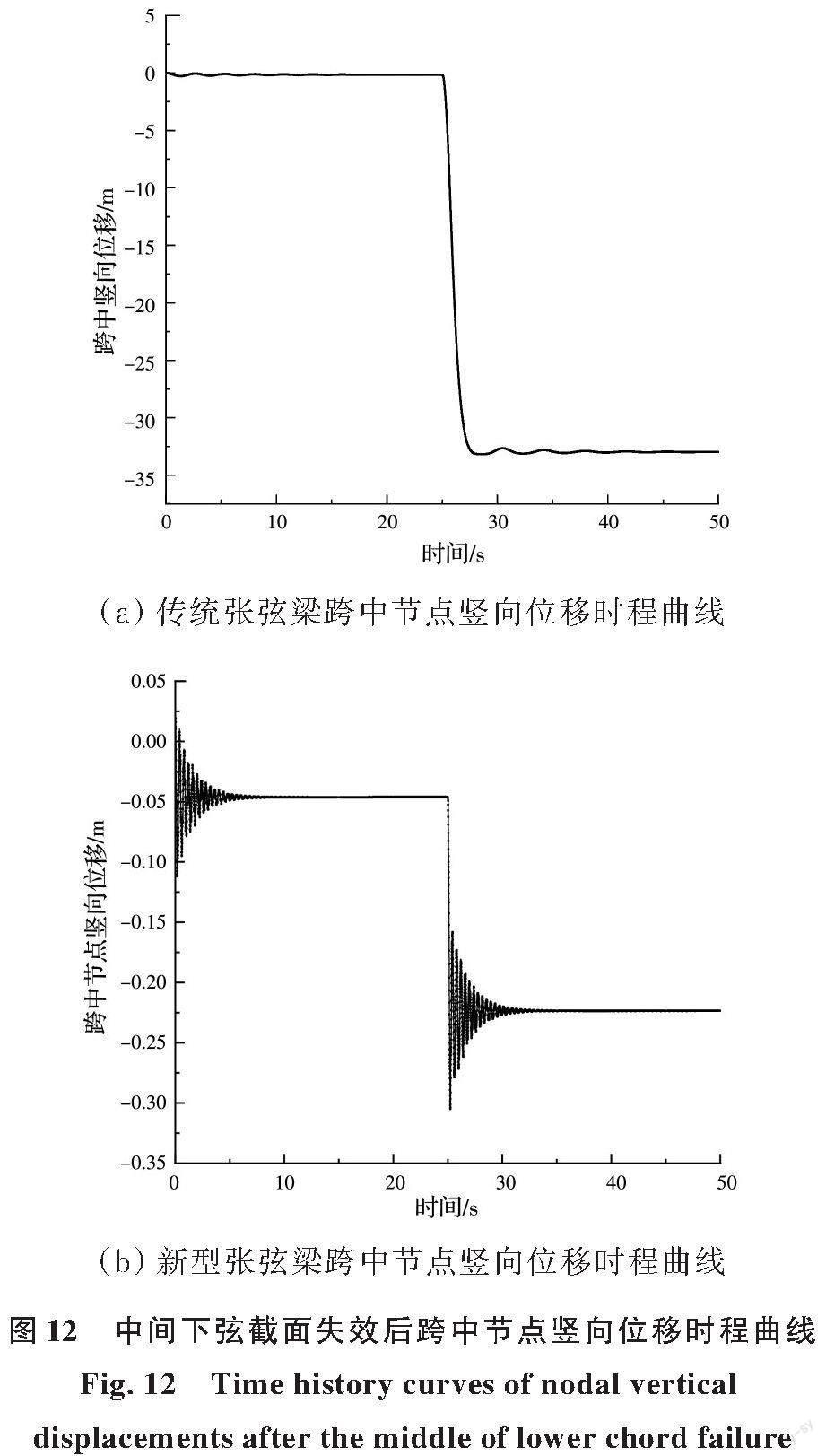
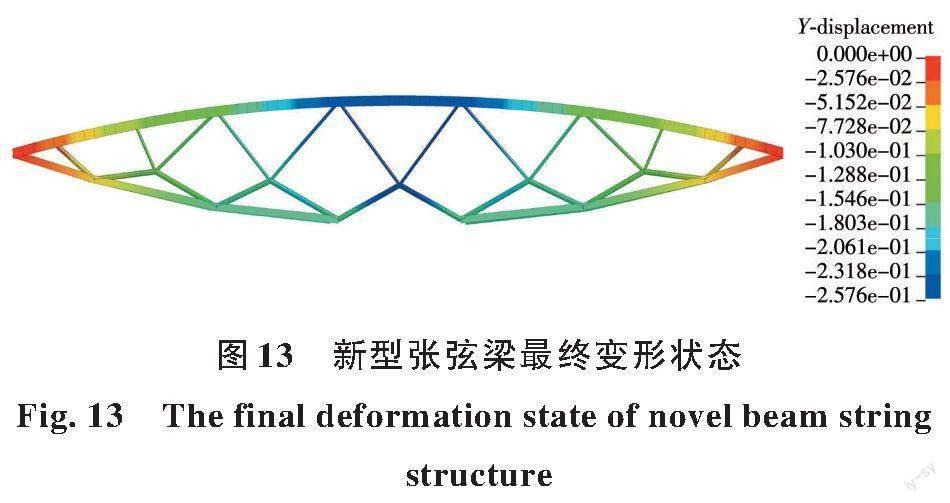
以中间下弦失效为例，采用考虑初始状态的等效荷载瞬时卸载法对传统张弦梁结构及新型张弦梁结构进行抗连续倒塌分析，提取两个模型上弦跨中节点的竖向位移时程及最终变形状态，分别如图12、图13所示。

由图12（a）可知，下弦失效后，传统张弦梁跨中竖向位移急剧增加，最大值达到33.2 m（由于该数值未考虑张弦梁结构与周围结构及地面的碰撞等因素，不一定与实际相符），表明传统张弦梁垮塌失效。图12（b）显示，下弦失效后，新型张弦梁跨中竖向位移虽有一定增加，但其最大跨中位移仅为0.305 m，最大跨中竖向位移与跨度之比为1/206，对比式（14）的倒塌判定标准可知，新型张弦梁结构未发生垮塌。

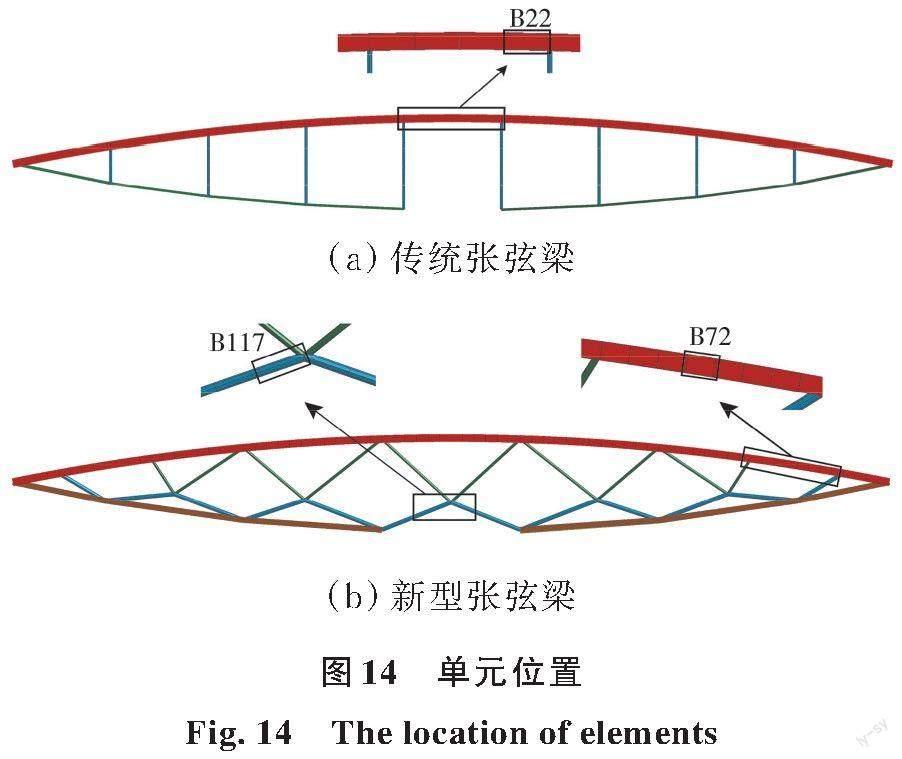
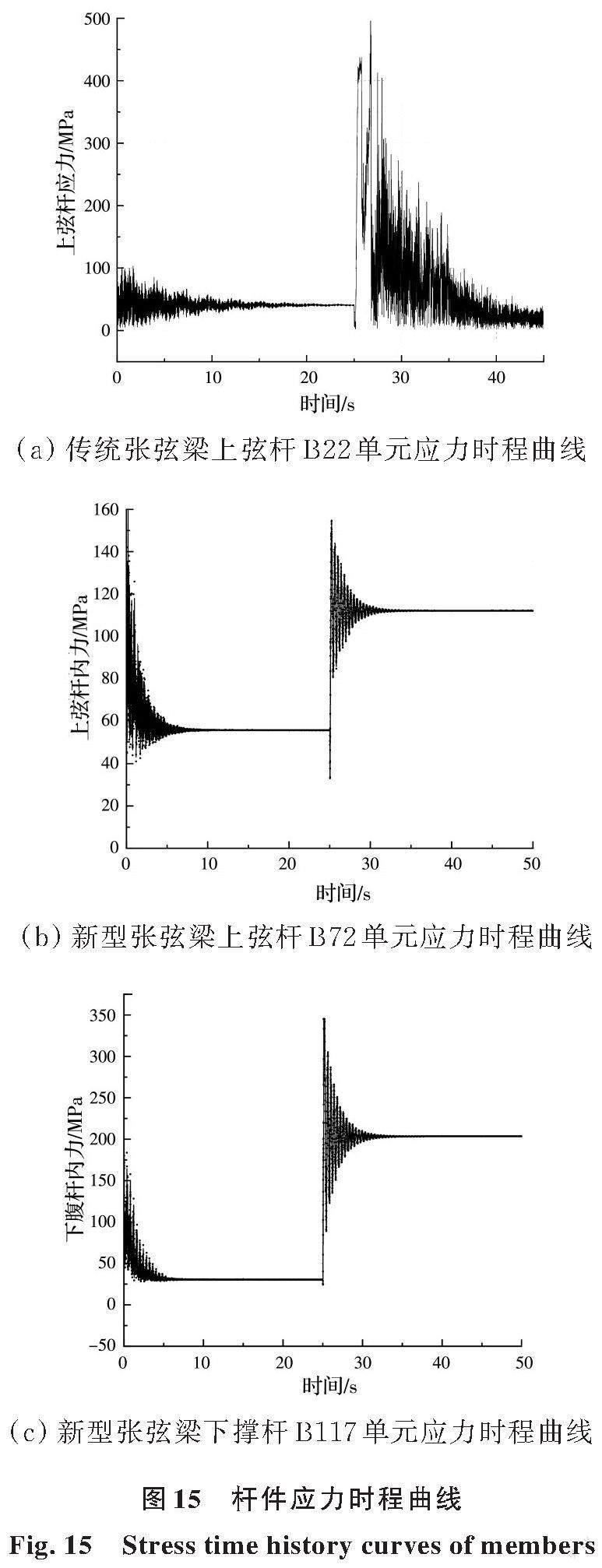
跨中下弦失效后，新型张弦梁交叉撑杆与下弦钢杆所组成的备用受力路径开始工作，使得结构发生应力重分布。拆除构件后，剩余结构各杆件应力均发生较大的动态增幅，并在阻尼作用下逐渐稳定。杆件作为张弦梁下弦失效前受力的关键构件，上弦杆的等效应力时程结果反映了张弦梁剩余结构内力重分布情况，如图14所示，受力全过程中传统张弦梁与新型张弦梁上弦杆危险单元分别为B22单元与B72单元，其单元应力时程曲线见图15（a）、（b）；对于新型张弦梁结构，下弦截面失效后，下腹杆成为剩余结构继续正常受力的关键构件，因此，其等效应力时程结果反映了下弦失效后剩余结构安全工作的能力，结构受力全过程中下腹杆危险单元为B117单元，其单元应力时程曲线见图15（c）。

根据图15（a）、（b）可知，考虑动力效应后，跨中下弦失效前后B22单元应力值分别为38、496 MPa，即传统张弦梁上弦杆应力迅速增加至失效前的13倍，后快速减小，稳定在0附近，表明上弦杆已破坏；对于新型张弦梁结构，跨中下弦失效前后B72单元应力大小分別为55、155 MPa，两应力比值仅为2.8，且受力过程中其最大应力仅为传统张弦梁受力过程中最大应力的30%。由此可知，下弦截面失效对传统张弦梁结构的冲击作用较大，而备用受力路径的增设可大幅度减小下弦截面失效对结构的冲击作用。

结合图15（c），考虑动力效应后，跨中下弦截面失效前后下部撑杆B117单元的应力值分别为26、345 MPa，失效前后应力比为13.6，这与不考虑动力效应时内力最大可增加至13.3倍（表3）的计算结果较为吻合。由于模型设计时赋予了下部撑杆较大的承载余量，且考虑到动力计算中应变率对材料强度的放大效应，将材屈服强度的动力放大系数取为1.1[15]。因此，当跨中下弦截面失效后，下部撑杆尚未达到破坏强度。

综上所述，经合理设计后，交叉撑杆和下弦钢杆组合使用可有效削弱下弦突然失效对结构的冲击作用，提高结构的抗连续倒塌能力。

3 新型张弦梁结构抗连续倒塌性能参数分析

改變新型张弦梁部分设计参数，开展交叉节点位置及撑杆数量等因素对新型张弦梁结构抗连续倒塌性能的影响分析。

3.1 交叉撑杆节点位置对倒塌性能的影响

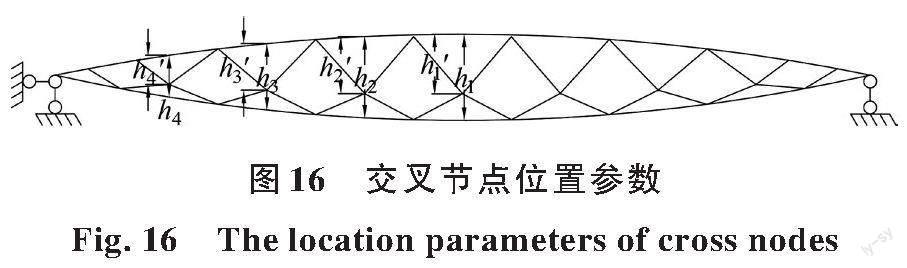
当下弦任意截面失效后，交叉撑杆的布置使得结构在失效段形成空腹桁架，提高了剩余结构的抗弯能力。下部撑杆作为该空腹桁架的下弦，成为剩余结构保持抗弯承载力的关键构件，在下弦失效前后内力增量较大。根据节点平衡条件，交叉撑杆节点位置对剩余结构的抗弯效率具有一定影响。如图16所示，定义交叉撑杆节点与上弦杆竖向相对位置参数Δ，即

式中：hi'为各交叉节点至上弦轴线的垂直距离；hi为各交叉节点位置处上弦轴线与下弦轴线的垂直距离；n为该类交叉节点的组数。对于给定的新型张弦梁结构，分析时假定各组交叉节点的Δ值相同。

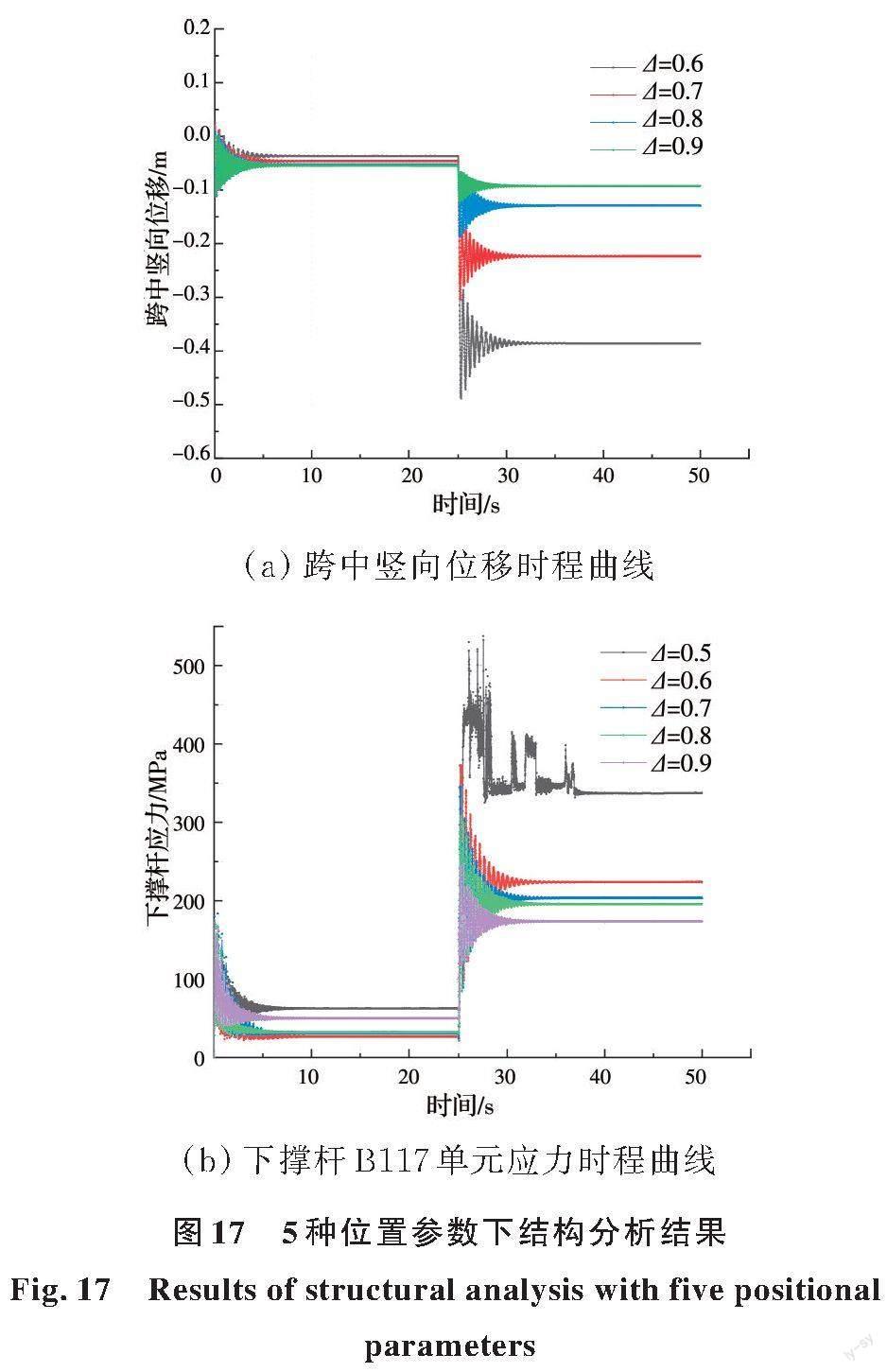
Δ取0.5、0.6、0.7、0.8、0.9，建立5个不同的新型张弦梁结构模型进行抗连续倒塌非线性动力分析，结果如图17所示。

对于新型张弦梁分析模型，当Δ=0.5时，结构发生完全垮塌。根据图17（a）可知，当Δ在0.6～0.9范围内变化时，跨中节点处最大竖向位移分别0.489、0.305、0.188、0.121 m，对应的位移与跨度之比分别为1/129、1/206、1/276、1/520。以式（14）作为连倒塌判别依据，4种结构均未发生连续倒塌，其中交叉撑杆位置参数Δ越大，剩余结构的抗弯效率越高，结构在下弦失效后的变形越小，抗连续倒塌性能越强。

由图17（b）可见，当交叉撑杆节点位置参数Δ=0.5时，B117单元发生破坏，下撑杆失效。Δ在0.6～0.9范围内变化时，下弦失效后下撑杆B117单元受到的最大应力分别为373、345、307、240 MPa。由此可知，交叉撑杆节点越靠近下弦，下撑杆受力越安全。原因在于，下弦失效后，Δ越大即下撑杆与下弦杆间的角度越小，剩余结构空腹桁架作用越明显。因此，增大Δ对于下撑杆以备用路径参与结构抗倒塌工作时的受力更加有利。然而，增大Δ会加大下撑杆与下弦杆焊接的操作难度，故需根据实际情况确定交叉撑杆位置参数。

3.2 交叉撑杆数量对倒塌性能的影响

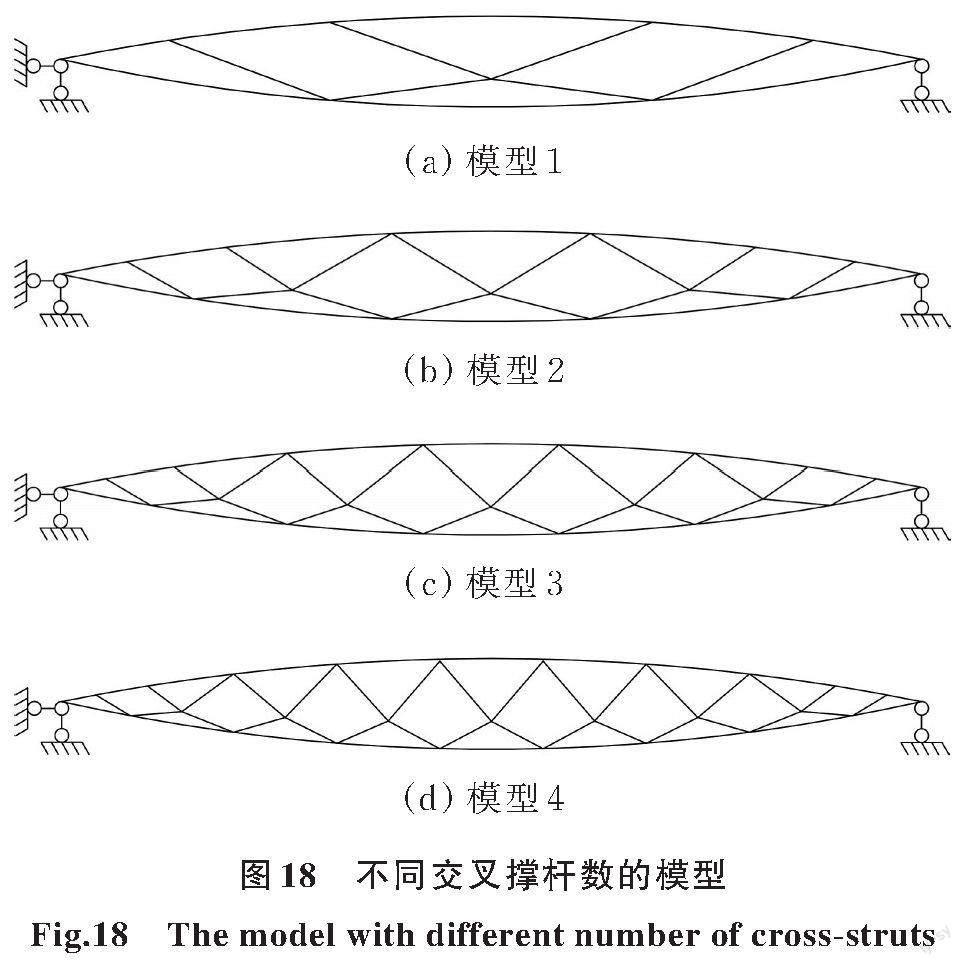
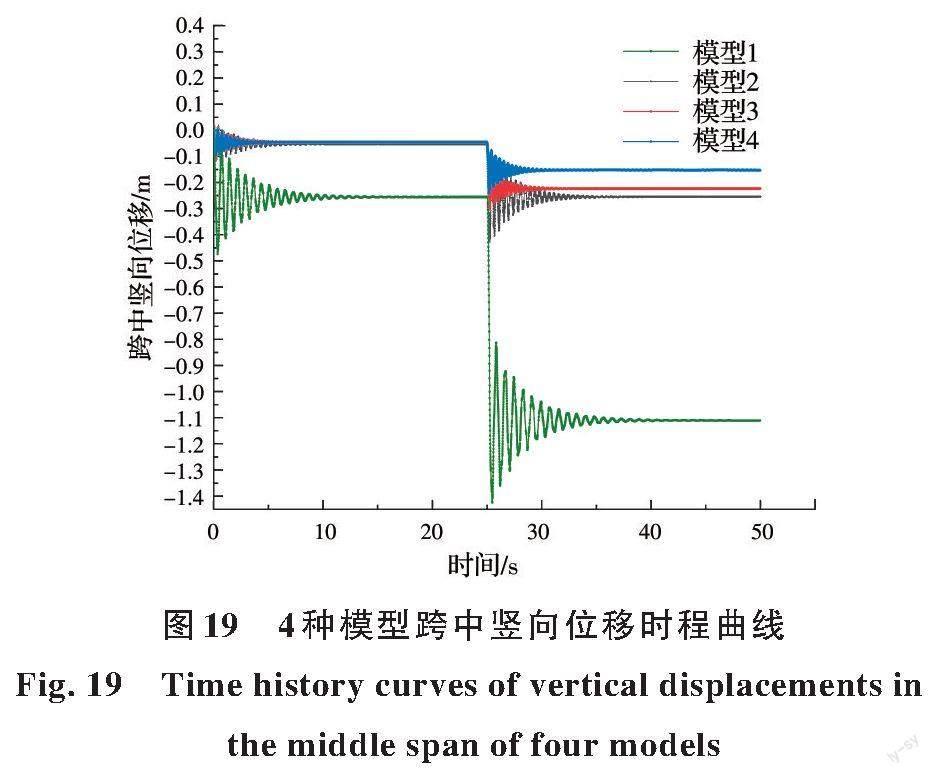
在下弦截面失效后，新型张弦梁依靠交叉撑杆与下弦钢杆组合提供备用受力路径，以提高张弦梁结构的冗余度。为明确交叉撑杆数量对新型张弦梁结构抗倒塌性能的影响规律，分别考虑撑杆数目为3、5、7、9组（单根边撑杆算1组），建立4种新型张弦梁结构模型，如图18所示，并进行抗连续倒塌非线性动力分析，结果如图19所示。

根据图19中的时程分析结果可知，模型1、2、3、4的最大竖向位移分别为1.42、0.426、0.305、0.242 m，最大竖向位移与跨度之比分别为1/44、1/148、1/206、1/260。由此可知，交叉撑杆数量越多，新型张弦梁冗余度越高，抗连续倒塌能力越强，且当撑杆组数大于5时，其抗连续倒塌能力较好。

4 结论

针对传统张弦梁结构抗连续倒塌性能较弱的特点，提出一种基于下弦和撑杆新构型的张弦梁结构。采用等效荷载瞬时卸载法对新型张弦梁结构抗连续倒塌性能进行研究，得到以下结论：

1）下弦任一截面失效后，新型张弦梁结构中交叉撑杆代替失效处下弦为结构提供备用传力路径，提高了张弦梁抗连续倒塌性能。

2）撑杆交叉节点越靠近下弦，剩余结构空腹桁架作用越明显，下部撑杆受力越优化。

3）结构交叉撑杆组数量越多，其冗余度越高，且交叉撑杆组数大于5时，结构抗连续倒塌性能较好。

参考文献

[1]  ADAM J M， PARISI F， SAGASETA J， et al. Research and practice on progressive collapse and robustness of building structures in the 21st century [J]. Engineering Structures， 2018， 173： 122-149.

[2]  陈骥. 美国哈特福德城体育馆网架结构失稳事故分析[J]. 钢结构， 1997， 12（4）： 20-25， 42.

CHEN J. On the analysis of American Hartford coliseum space truss roof stability failure [J]. Steel Construction， 1997， 12（4）： 20-25， 42. （in Chinese）

[3]  蒋友宝. 雪灾下轻钢结构大面积破坏的概率成因[J]. 土木建筑与环境工程， 2012， 34（3）： 65-69.

JIANG Y B. Probability analysis of failure cause for light-weight steel structure under snow disaster [J]. Journal of Civil， Architectural & Environmental Engineering， 2012， 34（3）： 65-69. （in Chinese）

[4]  ZHANG X H， LONG H F， ZHANG J Y， et al. Damage assessment and progressive collapse resistance of a long-span prestressed double-layer composite torsional reticulated shell [J]. Symmetry， 2020， 12（9）： 1434.

[5]  SONG B I， SEZEN H. Experimental and analytical progressive collapse assessment of a steel frame building [J]. Engineering Structures， 2013， 56： 664-672.

[6]  ZHAO X Z， YAN S， XU Z Y， et al. Research and application of beam string structures [J]. Structural Engineering International， 2015， 25（1）： 26-33.

[7]  胡帅领. 张弦结构连续倒塌分析与抗倒塌设计[D]. 北京：北京工业大学， 2010： 1-154.

HU S L. Progressive collapse analysis and anti-collapse design of beam string structure [D]. Beijing： Beijing University of Technology， 2010： 1-154. （in Chinese）

[8]  蔡建国， 朱奕锋， 冯健， 等. 撑杆失效对张弦结构抗连续倒塌性能的影响[J].建筑结构学报， 2015， 36（6）： 78-85， 100.

CAI J G， ZHU Y F， FENG J， et al. Influence of loss of struts on progressive collapse resistance performance of string structures [J]. Journal of Building Structures， 2015， 36（6）： 78-85， 100. （in Chinese）

[9]  曾滨， 陆金钰， 董霄， 等. 增设备用索对张弦桁架抗连续倒塌性能影响研究[J]. 空间结构， 2017， 23（4）： 49-54.

ZENG B， LU J Y， DONG X， et al. Progressive collapse resistance of truss string structures when installing fuse cables [J]. Spatial Structures， 2017， 23（4）： 49-54. （in Chinese）

[10]  ZHOU H， JIANG Y B， ADHIKARI S， et al. Comparisons of design methods for beam string structure based on reliability and progressive collapse analysis [J]. Structures， 2021， 33： 2166-2176.

[11]  余佳亮. 无站台柱张弦桁架雨棚结构性能分析与倒塌模拟研究[D]. 杭州： 浙江大学， 2012.

YU J L. Performance analyze and collapse research of non-platform-column truss string shelters [D]. Hangzhou： Zhejiang University， 2012. （in Chinese）

[12]  蒋友宝， 周浩， 康维， 等. 基于抗连续倒塌性能的张弦梁结构撑杆构型与数值验证[J].建筑结构学报. 2021， 42（Sup1）： 75-83.

JIANG Y B， ZHOU H， KANG W， et al. Anti-progressive collapse performance-based novel strut configurations of beam string structure and its numerical verification [J]. Journal of Building Structures， 2021， 42（Sup1）： 75-83. （in Chinese ）

[13]  馬克俭， 郑涛， 周观根. 成都“新世纪”国际会议会展中心钢结构工程简介[C]//第五届全国现代结构工程学术研讨会论文集. 广州， 2005： 214-225.

MA K J， ZHENG T， ZHOU G G. Brief introduction of steel structure project of Chengdu "new century" international conference and exhibition center [C]//Proceedings of the 5th National Symposium on modern structural engineering. Guangzhou， 2005： 214-225. （in Chinese）

[14]  薛伟辰， 刘晟， 苏旭霖， 等. 上海源深体育馆预应力张弦梁优化设计与试验研究[J]. 建筑结构学报， 2008， 29（1）： 16-23.

XUE W C， LIU S， SU X L， et al. Design optimization and experimental study on prestressed beam string of Shanghai Yuanshen Arena [J]. Journal of Building Structures， 2008， 29（1）： 16-23. （in Chinese）

[15]  蔡建国， 王蜂岚， 冯健， 等. 大跨空间结构连续倒塌分析若干问题探讨[J]. 工程力学， 2012， 29（3）： 143-149.

CAI J G， WANG F L， FENG J， et al. Discussion on the progressive collapse analysis of long-span space structures [J]. Engineering Mechanics， 2012， 29（3）： 143-149. （in Chinese）

[16]  钱凯， 李治， 翁运昊， 等. 后浇整体式预制混凝土梁-板子结构抗连续倒塌机理研究[J]. 建筑结构学报， 2021， 42（7）： 183-193.

QIAN K， LI Z， WENG Y H， et al. Load resisting mechanisms of assembled monolithic precast concrete beam-slab substructures to resist progressive collapse [J]. Journal of Building Structures， 2021， 42（7）： 183-193. （in Chinese）

[17]  LS-DYNA® Keyword User，s Manual Volume Ⅱ： Material Models [M]. California： Livermore Software Technology Corporation， 2013.

[18]  张士昌. 成都新国际会展中心空间钢屋盖结构优化研究[D]. 南京： 东南大学， 2005.

ZHANG S C. Optimization study on spatial steel roof structure of Chengdu international meeting and exhibition center [D]. Nanjing： Southeast University， 2005. （in Chinese）

[19]  建筑结构抗连续倒塌规范： CECS 392： 2014 [S]. 北京： 中国计划出版社， 2014.

Code for anti-collapse design of building structures： CECS 392：2014 [S]. Beijing： China Planning Press， 2014. （in Chinese）

[20]  蔡建国， 王蜂岚， 冯健， 等. 新广州站索拱结构屋盖体系连续倒塌分析[J]. 建筑结构学报， 2010， 31（7）： 103-109.

CAI J G， WANG F L， FENG J， et al. Progressive collapse analysis of cable-arch structures of the New Guangzhou Railway Station [J]. Journal of Building Structures， 2010， 31（7）： 103-109. （in Chinese）

[21]  LU Y， LIU K， WANG Z L， et al. Dynamic behavior of scaled tubular K-joints subjected to impact loads [J]. Marine Structures， 2020， 69： 102685.

[22]  蒋瓅， 倪建公， 瞿革， 等. 复杂高层钢结构抗连续倒塌能力分析关键技术研究[J]. 建筑结构学报， 2019， 40（6）： 155-165.

JIANG L， NI J G， QU G， et al. Study on key issues of progressive collapse resistance capacity analysis for complex high-rise steel structure [J]. Journal of Building Structures， 2019， 40（6）： 155-165. （in Chinese）

[23]  蔣友宝， 刘志， 贺广零， 等. 考虑脉动风场的3 MW风机钢塔筒基础底板脱开失效概率[J]. 工程力学， 2021， 38（5）： 199-208.

JIANG Y B， LIU Z， HE G L， et al. Failure probability of foundation slab void for 3 MW wind turbine steel tower considering turbulent wind field [J]. Engineering Mechanics， 2021， 38（5）： 199-208. （in Chinese）

[24]  US General Services Administration （GSA）. Progressive collapse analysis and design guide lines for new federal office buildings and major modernization projects [S]. Washington D C： GSA， 2003.

[25]  MOZOS C M， APARICIO A C. Numerical and experimental study on the interaction cable structure during the failure of a stay in a cable stayed bridge [J]. Engineering Structures， 2011， 33（8）： 2330-2341.