管节点冲剪校核影响因素分析

冯自进

（北京高泰深海技术有限公司 天津分公司，天津 300451）

管节点在海洋石油平台中应用十分广泛，管节点的冲剪校核是计算分析的重点［1-4］。目前，海洋石油平台管节点冲剪校核一般通过结构计算软件SACS自动计算，而SACS软件计算原理是基于不同版本的 API PR 2A《Recommended Practice for Planning，Designing and Constructing Fixed Offshore Platforms—Working Stress Design》［5-8］编制的。对于当管节点冲剪校核计算结果超出API PR 2A范围时该如何调整，冲剪校核计算结果与弦杆和撑杆的管径、壁厚及荷载的关系等问题，SACS软件和API PR 2A中均未做明确说明。文献［9］分析了API PR 2A修订版对管节点的影响。文献［10］采用ANSYS有限元的方法分析了撑杆与弦杆的直径比、径厚比和壁厚比对K型和T型管节点极限承载力的影响。文献［11］虽然分析了管节点冲剪校核与弦杆壁厚、撑杆管径和壁厚的关系，但是未对弦杆和撑杆的荷载因素进行分析，也未细分撑杆受压和受拉的情况，而撑杆受拉或者受压时管节点冲剪校核结果相差很大。文中基于最新版本的API PR 2A—2014［8］以及文献［12-13］，对常见的T/Y型管节点冲剪校核结果影响因素进行分析。

1 管节点冲剪校核基本原理

1.1 管节点结构

常见的简单T/Y型管节点结构见图1。图中θ为撑杆与弦杆的夹角，t为撑杆壁厚，T为弦杆壁厚，d为撑杆直径，D为弦杆直径。

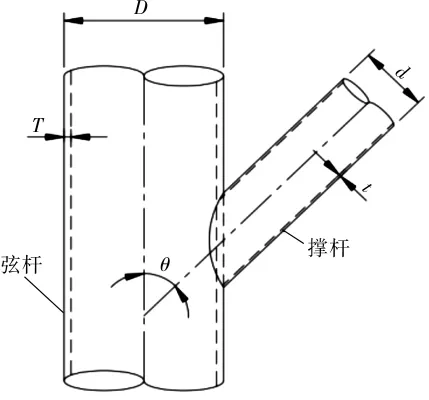
图1 简单T/Y型管节点结构示图

1.2 冲剪校核公式

根据API PR 2A—2014，T/Y型管节点的冲剪校核一般需要进行Strength UC和Load UC校核。Strength UC校核中，Ustrn为撑杆50%或100%的轴向极限承载能力 （应用于地震韧性分析且强度分析时地面地震加速度大于0.1g）［14］与许用轴向荷载的比值。当取100%轴向荷载时，Ustrn计算式为：

其中

Load UC校核中，节点UC值IR可直接由API PR 2A—2014得出：

其中

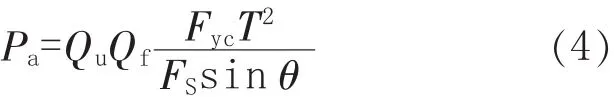
式（1）～式（5）中，Fyb、Fyc分别为撑杆和弦杆在节点处的屈服强度或0.8倍的抗拉强度二者中的最小值，MPa；Ab为撑杆有效横截面面积，m2；Pa为撑杆的许用轴向荷载，P为撑杆的轴向荷载，kN；Ma为撑杆的许用弯距，M为撑杆的轴向弯矩，kN·m；Qu为极限强度系数，Qf为弦杆荷载系数；FS为安全系数，一般工况取1.6，地震工况取1.0。下标ipb表示平面内，opb表示平面外。

从式（3）可知，IR的大小随着撑杆荷载P和M的增大而增大。从式（4）和式（5）可知，撑杆的许用荷载随着撑杆与弦杆夹角θ（不大于90°）的减小而增大， 随着 Qu、Qf、Fyc和 T的增大而增大。因此，要增大撑杆的许用荷载，可以减小撑杆与弦杆的夹角、增大弦杆的厚度或增强弦杆的材质［15］（弦杆材质屈服强度不能大于500 MPa），同时也可以增大Qf和Qu。

1.3 弦杆荷载系数Qf

弦杆荷载系数Qf由下式给出［8］：

其中

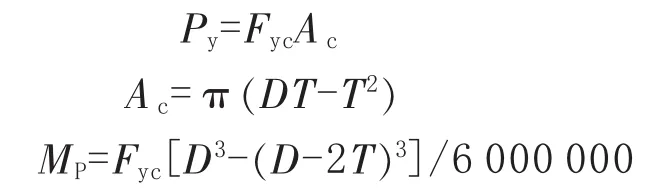
式（6）～式（7）中，C1、C2和 C3为与管节点类型和荷载形式有关的系数，对于承受撑杆轴向荷载的T/Y型管节点，C1=0.3、C2=0、C3=0.8；对于承受撑杆弯矩荷载作用下的所有类型节点，C1=0.2、C2=0、C3=0.4；PC为弦杆的轴向荷载，Py为弦杆的极限轴向荷载，kN；Mipb为弦杆平面内弯矩，MP为弦杆的极限弯矩，MC为弦杆总弯矩（大小为平面内弯矩与平面外弯矩平方和的平方根），kN·m。

式（6）化简得：

1.4 极限强度系数Qu

T/Y型管节点极限强度系数Qu与撑杆荷载大小没有关系，但与撑杆所受的荷载形式有关。API PR 2A—2014中T/Y型管节点强度系数Qu的计算式见表 1。 表 1 中 β=d/D、γ=D/（2T）。

表1 API PR 2A—2014中T/Y型管节点强度系数Qu计算式

从表1可以看出，当撑杆轴向压缩时，2.8+（20+0.8γ）β1.6≤2.8+36β1.6， 则 γ≤20。而 API PR 2A—2014表7.1中要求10≤γ≤50。综合考虑，有10≤γ≤20。

2 T/Y型管节点Strength UC校核

2.1 Ustrn计算公式

根据上述分析，经过换算可以得出T/Y型管节点Strength UC校核的Ustrn为：

当弦杆所受到的荷载保持不变时，将式（8）和表1中的Qu计算式代入式 （9），可以得到Ustrn与D、T、d、t的函数关系式。

2.2 Ustrn与撑杆壁厚t关系

假设 PC=-20 000 kN、Mipb=10 000 kN·m、D=1 382 mm、T=60 mm、d=610 mm、θ=π/2、Fyb=Fyc=355 MPa。 根据 API PR 2A—2014，20≤d/t≤60，则10.2 mm≤t≤30.5 mm。T/Y型管节点的Ustrn与撑杆壁厚t的关系曲线见图2。

图2 T/Y型管节点Ustrn与撑杆壁厚t关系曲线

从图2可以看出，不管撑杆是受压还是受拉，当其余条件不变时，T/Y型管节点的Ustrn值均随撑杆壁厚t的减小而减小，且撑杆受拉的Ustrn值小于撑杆受压的Ustrn值。

2.3 Ustrn与撑杆直径d关系

假 设 PC=-20 000 kN、Mipb=10 000 kN·m、D=1 382mm、T=60mm、t=19mm、θ=π/2、Fyb=Fyc=355MPa。根据 API PR 2A—2014，20≤d/t≤60 且 0.2≤β≤1，则 380 mm≤d≤1 140 mm。T/Y 型管节点的 Ustrn与撑杆直径d的关系曲线见图3。

图3 T/Y型管节点Ustrn与撑杆直径d关系曲线

从图3可以看出，在其余条件不变情况下，撑杆受拉时，T/Y型管节点的Ustrn值随着撑杆直径d的增大而增大；撑杆受压时，随着撑杆直径d的增大，Ustrn值先增大，当增大到一定数值时，又随着撑杆直径d的增大而减小。

2.4 Ustrn与弦杆壁厚T关系

假 设 PC=-20 000 kN、Mipb=10 000 kN·m、D=1 382 mm、d=610 mm、t=19 mm、θ=π/2、Fyb=Fyc=355 MPa。 根据 API PR 2A—2014，20≤D/t≤60 且10≤γ≤20，则 34.55 mm≤T≤69.1 mm。 T/Y 型管节点的Ustrn与弦杆壁厚T的关系曲线见图4。

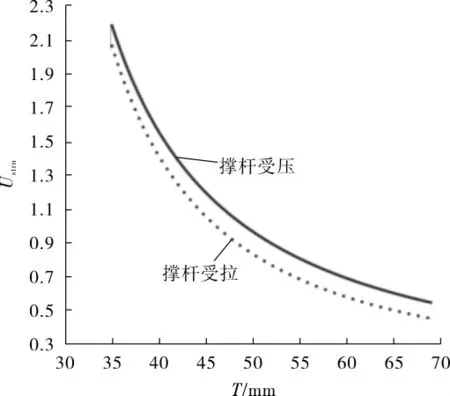
图4 T/Y型管节点Ustrn与弦杆壁厚T关系曲线

从图4可以看出，当其余条件不变时，无论撑杆是受压还是受拉，弦杆壁厚T越大，T/Y型管节点的Ustrn值越小。

2.5 Ustrn与弦杆直径D关系

假设 PC=-20000kN、Mipb=10000kN·m、T=60mm、d=610 mm、t=19 mm、θ=π/2、Fyb=Fyc=355 MPa。根据API PR 2A—2014，20≤D/T ≤60、0.2≤β ≤1 且10≤γ≤20，则 1 200 mm≤D≤2 400 mm。T/Y 型管节点的Ustrn与弦杆直径D的关系曲线见图5。

图5 T/Y型管节点Ustrn与弦杆直径D关系曲线

从图5曲线可以看出，当其余条件不变时，无论撑杆是受拉还是受压，随着弦杆直径D的增大，T/Y型管节点的Ustrn值均先小幅减小，之后开始逐渐增大。

3T/Y型管节点LOAD UC校核

在T/Y型管节点LOAD UC校核中，求解IR时，撑杆许用弯矩Ma和许用轴向荷载Pa的弦杆荷载系数Qf是不同的。

求解许用轴向荷载Pa时，取Qf计算式中的C1=0.3、C2=0、C3=0.8，则有：

求解许用许用弯矩Ma时，取Qf计算式中的C1=0.2、C2=0、C3=0.4，则有：

将式（10）、式（11）和表 1 中的 Qu分别代入到式（3）中，同样可以得到 IR与 D、T、d的函数关系式，且IR的数值大小与撑杆壁厚t无关。

3.1 IR与撑杆直径d关系

假 设 PC=-20 000 kN、Mipb=10 000 kN·m、P=±9 000 kN、撑杆平面内弯矩 Mbipb=-1 500 kN·m、撑杆 平 面 外 弯 矩 Mbopb=-1 000 kN·m、D=1 382 mm、T=60 mm、θ=π/2、Fyb=Fyc=355 MPa。 根 据 API PR 2A—2014，0.2≤β≤1，则 276.4 mm≤d≤1 382 mm。

T/Y型管节点的IR与撑杆直径d的关系曲线见图6。

图6 T/Y型管节点IR与撑杆直径d关系曲线

从图6可以看出，在其余条件不变时，无论撑杆是受拉还是受压，T/Y型管节点的IR值均随撑杆管径d的增大而减小。

3.2 IR与弦杆壁厚T关系

假 设 PC=-20 000 kN、Mipb=10 000 kN·m、P=±9 000 kN、Mbipb=-1 500 kN·m、Mbopb=-1 000 kN·m、D=1 382 mm、d=610 mm、θ=π/2、Fyb=Fyc=355 MPa。根据 API PR 2A—2014，20≤D/T≤60 且 10≤γ≤20，则34.55 mm≤T≤69.1 mm。T/Y型管节点的IR与弦杆壁厚T的关系曲线见图7。

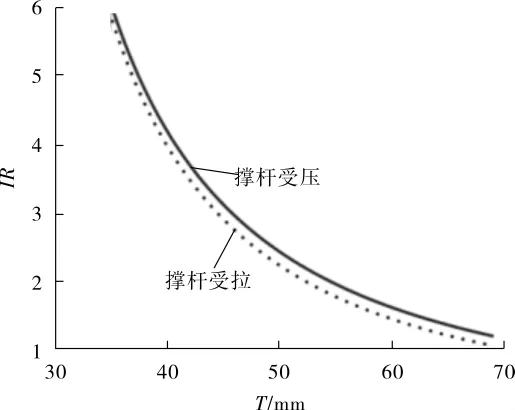
图7 T/Y型管节点IR与弦杆壁厚T关系曲线

从图7可以看出，在其余条件不变时，T/Y型节点的IR值随着弦杆壁厚T的增大而减小。

3.3 IR与弦杆直径D关系

假 设 PC=-20 000 kN、Mipb=10 000 kN·m、P=±9 000 kN、Mbipb=-1 500 kN·m、Mbopb=-1 000 kN·m、d=610 mm、θ=π/2、Fyb=Fyc=355 MPa。 根据 API PR 2A—2014，20≤D/T≤60、0.2≤β≤1 且 10≤γ≤20，则 1 200 mm≤D≤2 400 mm。

T/Y型管节点的IR与弦杆直径D的关系曲线见图8。

图8 T/Y型管节点IR与弦杆直径D关系曲线

从图8可以看出，其余条件不变时，随着弦杆直径D的增大，T/Y型管节点的IR值先小幅减小，之后逐渐增大。

4 结语

在T/Y型管节点的Strength UC和Load UC冲剪校核中，①Ustrn值与撑杆荷载的大小没有关系，但与撑杆所受轴向荷载方向有关，一般情况下撑杆轴向受压的Ustrn值大于轴向受拉的Ustrn值。IR值随着撑杆荷载的减小而减小。②当弦杆轴向荷载受压时，受压荷载越小，相应的IR值与Ustrn值越小。当弦杆轴向荷载受拉，且受拉荷载等于C1Py/(2C3Fs)时，撑杆许用荷载有最大值，即IR值和Ustrn值最小，此时相应增大或减小弦杆的轴向受拉荷载，都会增大IR与Ustrn的数值。

在弦杆和撑杆荷载保持不变的情况下，①无论撑杆轴向受拉还是受压，Ustrn值均随撑杆壁厚t的减小而减小，而IR值与撑杆壁厚t无关。②当撑杆受拉时，Ustrn值随撑杆直径d的减小而减小。当撑杆受压时，Ustrn值先随撑杆直径d的增大而增大，当达到极值后，随撑杆直径d的增大而减小。无论撑杆是受拉还是受压，IR值均随撑杆直径d的增大而减小。③无论撑杆是受拉还是受压，IR值和Ustrn值均随弦杆壁厚T的增大而减小。④无论撑杆是受拉还是受压，IR值和Ustrn值均随弦杆直径D的增大先小幅减小，再逐渐增大。⑤IR值和Ustrn值还与撑杆和弦杆之间的夹角（不大于90°）及其材质有关。夹角越大，IR值和Ustrn值越大；材料的屈服强度越大，IR值和Ustrn值越小。需要注意的是，这些结论是在弦杆和撑杆所受荷载不变的基础上得出的，在实际工程中，当改变弦杆或撑杆的直径、壁厚或者夹角时，都有可能引起撑杆和弦杆荷载的重新分布，需具体问题具体分析。