水-短链醇二元溶液的表面吸附

于先超， 亓文帅， 邓全花， 侯万国，3

水-短链醇二元溶液的表面吸附

于先超1， 亓文帅1， 邓全花2， 侯万国1，3

（1. 山东大学胶体与界面化学教育部重点实验室， 2. 化学与化工学院， 3. 国家胶体材料工程技术研究中心, 济南 250100）

基于表面聚集吸附(SAA)模型和Gibbs吸附微分方程, 建立了二元液体混合物Gibbs表面过剩(2)和吸附层厚度()代数方程, 可在全浓度范围内预测2和随体相组成(如组分2的摩尔分数2,b)的变化. 采用所建立的模型, 研究了水(组分1)-短链醇(组分2)二元溶液的表面吸附行为, 其在水表面的吸附趋势按甲醇、 乙醇、 异丙醇、 正丙醇和叔丁醇的顺序依次增强, 与其疏水性增强趋势一致, 且其2和在低2,b区均依次增大, 而在高2,b区均依次减小, 是短链醇间吸附趋势和分子尺寸的差异所致. 对于给定的短链醇体系, 随着2,b的增大,2先急剧增大然后降低, 呈现一个最大值, 而其持续降低.

液体混合物； 表面吸附； 表面聚集； 吸附层厚度； 热力学模型

液体混合物的表面组成与其体相不同， 称为表面吸附（或富集）， 这是一个基本的界面现象， 因其具有重要的理论意义和应用价值而受到广泛关注［1～4］. 表面层组成（或表面过剩量）和吸附层厚度是表征表面吸附的两个重要物理量. 虽采用多种技术［如椭圆偏振［5，6］、 中子反射［7，8］、 质谱（联合表面层分子簇束产生装置）［9］、 频振动光谱［10］和亚稳态诱导电子光谱［11］等］探索测定表面层组成和厚度， 但目前仍难以（独立）获得准确数据［7，8］. 因液体混合物的表面张力易于准确测定， 因而目前相关研究主要集中于建立表面层组成和厚度与表面张力的相关性模型， 依据表面张力随体相组成的变化预测表面层组成和厚度的变化， 可以认识和描述表面吸附行为［8，12～15］.

基于热力学分析及经验或半经验归纳等， 已提出了很多模型用于描述或预测表面性质（如组成和厚度）与体相组成的相关性［16～23］. 但由于表面现象的复杂性， 现有模型还缺乏普适性， 缘于模型构建时的一些假设与体系实际状态不符［23～27］. 特别是， 对一些性质的预测甚至存在相反的结果. 如， 水-乙醇溶液作为模型体系得到广泛研究， 关于其表面层厚度随体相乙醇浓度增大的变化还存在争议， Azizian等［14］和Hyde等［8］认为逐渐降低（呈线性或指数衰减）， 而Bagheri等［12，13］和Santos等［15］认为是先升高后降低， 这主要是所用模型及其假设不同所致.

Butler方程、 Gibbs吸附方程和Langmuir等温式是表面热力学的3个基本方程［22～28］， 其中Gibbs和Langmuir方程相互独立， 但均可由Butler方程推出［28］. Butler方程将表面组成、 表面张力与体相组成相关联， 理论上可获得表面组成和厚度信息， 但目前尚未得到广泛应用， 因其涉及各组分的活度系数和偏摩尔面积［28，29］， 而这两个物理量也与体系组成有关， 目前还难以实验测定和理论预测［30～32］. Gibbs方程可给出表面过剩（吸附）量随体相组成的变化， 但不能直接给出表面组成信息［28］， 也存在溶质活度系数问题［25，26］. 另外， Gibbs方程是一个微分方程， 包含表面张力对溶质分子浓度的导数， 但其处理结果人为误差大. Langmuir等温式是一个关联表面相和体相组成的简单方程式［22，24，28］， 仅涉及一个物理意义明确的模型参数（即吸附平衡常数）， 但仅适用于组分性质相近的混合体系（或理想溶液， 因其假设活度系数 为1）. Piñeiro等［22］考虑体系的非理想性（组分分子尺寸差异及特殊相互作用）， 提出了“扩展Langmuir方程”（Extended Langmuir equation）. 需说明的是， 经典的和改进的Langmuir方程均未涉及表面张力， 在依据表面张力数据推测其吸附平衡常数时， 需与一个关联表面张力和表面组成的独立方程联用［22，23］. Eberhart［18］提出一个半经验“简单混合律”（Simple mixing rule）， 经Laaksonen和Kulmala［20］以及Piñeiro等［22］改进后， 常与扩展Langmuir方程联合描述二元液体混合物的表面张力等温线［22，23］. 表面张力和表面组成等温线（恒定温度下， 表面张力和组成随体相组成的变化线， 可统称为表面吸附等温线）可分为L型和S型， 扩展Langmuir方程难以准确描述S型等温线［23］.

现有预测表面组成和厚度的热力学模型或方法均基于上述3个基本方程（选取其中的两个方程联用）， 其差异主要是选取的方程组合以及假设（如活度系数和偏摩尔面积）不同［8，12～15］. 最近， 我们基于热力学吸附平衡原理和表面胶束化模型［33］， 提出了“表面聚集吸附”模型（Surface aggregation adsorption model， SAA）［23，34］. 活性组分易于表面（界面）聚集， 这已被理论和实验所证实［20，26，35］. SAA模型与改进的Eberhart混合律联用， 可准确描述液体混合物的L型和S型表面吸附等温线. SAA模型能否与Gibbs方程相关联， 合理预测液体混合物的表面吸附层厚度是一个值得研究的问题. 另外， 表面吸附（吸附能、 吸附量和吸附层厚度）的影响因素目前还不清晰， 有必要探索研究.

本文基于SAA模型和Gibbs微分方程， 推导出了Gibbs表面过剩和吸附层厚度代数方程， 可在全浓度范围内预测Gibbs表面过剩和吸附层厚度. 采用所建立的模型方程对水-短链醇（甲醇、 乙醇、 异丙醇、 正丙醇和叔丁醇）二元溶液的表面吸附进行了研究， 考察了其吸附行为的差异， 探究了其内在原因， 以期加深对液体表面吸附现象的认识.

1 理论分析

假设液体混合物的表面层为具一定厚度（）的均匀表面相［18， 23］（这是一个常用假设， 可简化模型处理； 实际上， 表面层在平行表面方向上是均匀的， 而在垂直表面方向上是不均匀的）. 为了表述方便， 按惯例将表面张力高的组分记为组分1（常称为溶剂）， 将表面张力低的组分记为组分2（常称为溶质或表面活性组分， 因其在表面富集）.

1.1　SAA模型

对二元液体混合物体系， SAA模型假设［23］： （1） 表面活性组分在表面层吸附而形成聚集体； （2） 表面层由吸附位（或准晶格）组成， 每个吸附位由一个溶剂分子或一个活性组分聚集体占据.

组分2的表面吸附（或与组分1的交换吸附）平衡可表示为

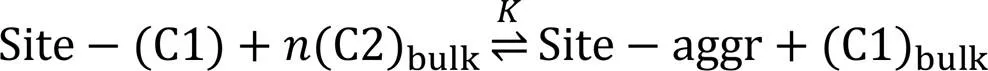
式中： Site表示吸附位（或准晶格）； C1和C2分别表示组分1和2的分子， aggr表示组分2的聚集体，为其平均聚集数（一个聚集体的分子数）， 下标“bulk”表示体相，为组分2与组分1的表面交换吸附平衡常数.

设各物种在体相和表面相的活度系数均为1， 依据热力学吸附平衡原理可知：

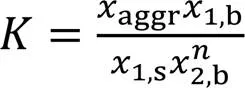
式中：1，s和aggr分别为组分1分子和组分2聚集体在表面相中的摩尔分数；1，b和2，b分别为组分1和组分2分子在体相中的摩尔分数， 下标“s”和“b”分别表示表面相和体相.

设聚集体的偏摩尔体积（aggr）与组分2的偏摩尔体积（2）关系为aggr=2， 则式（2）可写为

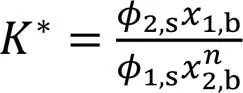
式中：1，s和2，s分别是组分1和组分2在表面相中的体积分数；*≡2/1（1为组分1的分子尺寸，2为组分2的分子尺寸）. 因1，s+2，s=1和1，b+2，b=1， 故由式（3）可推得SAA模型方程为［23］

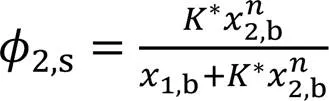
Connors和Wright提出“对比表面压”（Reduced surface pressure，r）概念［19，27］， 定义为

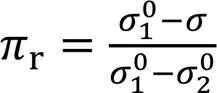
式中：为液体混合物的表面张力，10和20分别为纯组分1和纯组分2的表面张力. 用r可方便对比 不同液体混合物体系间表面张力（或吸附）行为的差异（因其值在0～1间变化）.

对二元体系， 经Laaksonen和Kulmala改进的Eberhart混合律方程为［20］

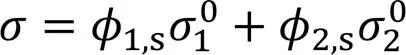
由此式可得，r=2，s， 这是改进Eberhart方程的一个优点， 由实验测定的值可得出表面相组成.

由式（4）～式（6）可得［23］：

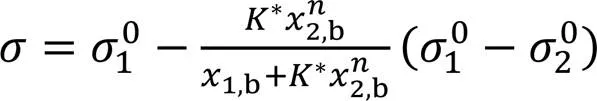
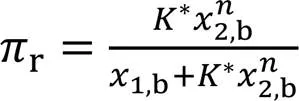
式（8）可写成线性式：

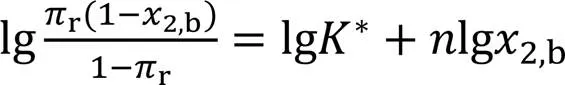
此式表明， lg［r（1‒2，b）/（1‒r）］对lg2，b作图为直线， 由其截距和斜率可求K和值. 两个参数（K和）均可由线性拟合得到唯一值， 这是该模型的一个优点［23］.

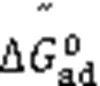
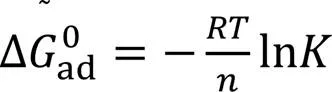
1.2　Gibbs表面过剩

表面过剩量（或表面吸附量）是一个相对概念， 表征表面相和体相组成的差异. 表面过剩有不同的定义［13，17］， 常用的是Gibbs表面过剩［12～14］. Guggenheim和Adam［17］揭示了Gibbs表面过剩概念的物理本质： 即单位面积表面层中溶质的量与其等量溶剂在体相时所含溶质的量之差（即基于等量溶剂定义的溶质表面过剩量）. Gibbs基于溶剂（组分1）过剩为零的分界面， 推出溶质（组分2）的表面过剩量［1］， 用2表示.

设溶质的活度系数为1， 则Gibbs吸附方程为［25，36］

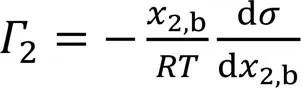
这是一个微分方程， 在获取d/d2，b值时人为误差较大［25， 36］.

将式（7）与式（11）联合可推导出：

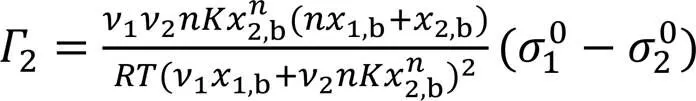
此式即为Gibbs过剩量的代数方程， 利用SAA模型得到的和值可在全浓度（2，b=0～1）范围内计算2值.

另外， 由式（12）可看出，2，b→0和2，b→1时的极限2值［分别用2（x→0）和2（x→1）表示］， 即

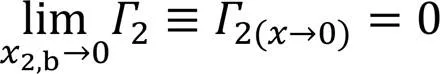
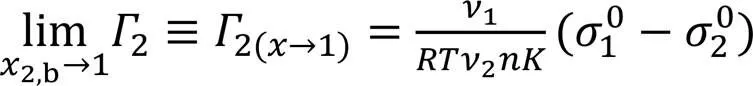
在2，b→0时，2=0， 而当2，b→1时，2>0， 这由2的物理本意所致［17］. 在全浓度范围内，2≥0， 溶质（低表面张力组分）为正吸附.

1.3　吸附层厚度

现基于Gibbs方程和SAA模型建立吸附层厚度（Adsorption layer thickness）方程， 简称ALT方程. 根据Gibbs表面过剩的物理本意［17］，2可表示为［12］

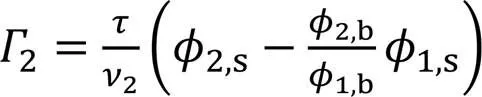
由式（3）， 式（4）， 式（12）和式（15）可得ALT方程为

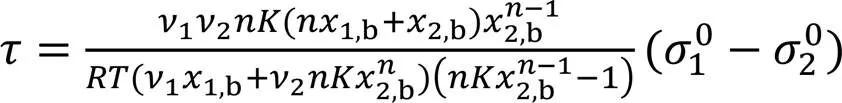
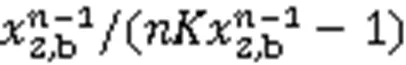
由式（16）可看出，2，b→0时的极限值（τ→0， 设n→0=1）为

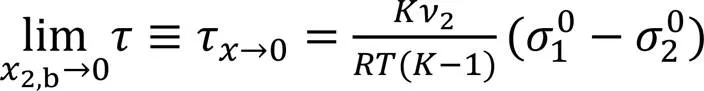
在2，b→1时的极限值（τ→1）为

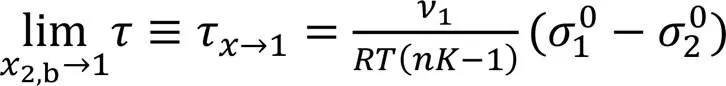
由式（16）～式（18）可以看出，随（吸附趋势）的增大而减小；τ→0（或低2，b区的）随2的增大而增大（若>>1时，则与无关）， 而τ→1与2无关（与1有关）. 需说明的是， 当=1和=1时， 可视为理想体系， 不发生吸附， 其→∞（或不存在明确的吸附层； 吸附层不是表面层）.

1.4　模型拟合

采用Origin 2023b（学习版）软件对实验数据进行模型方程拟合， 采用平均相对偏差（Average relative deviation， ARD）和平均绝对偏差（Average absolute deviation， AAD）评判模型预测与实验数据间的符合度. ARD和AAD计算式为［23，34］

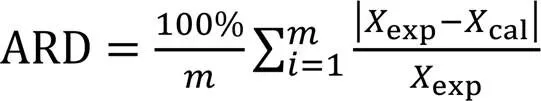
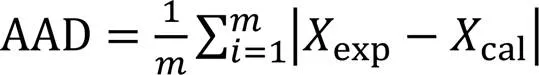
式中：exp和cal分别是物理量的实验值和模型计算值；为数据点数.

2 结果与讨论

采用所建立的模型方程研究了短链醇甲醇（MeOH）、 乙醇（EtOH）、 异丙醇（PrOH）、 正丙醇（PrOH）和叔丁醇（BuOH）与水（Water）的二元液体混合物的表面吸附行为. 表1列出了所涉及纯液体在25 ℃下的摩尔体积（0）、 表面张力（0）以及溶度参数（）值［25，37～39］. 其中，参数包括Hildebrand参数（t）及其Hansen色散（d）、 极性（p）和氢键分量（h）， 用于计算组分间的Flory-Huggins参数（12）， 以考察其相互作用强度（或相似度）［40］. 另外， 在模型计算时， 各组分的偏摩尔体积用其0代替.

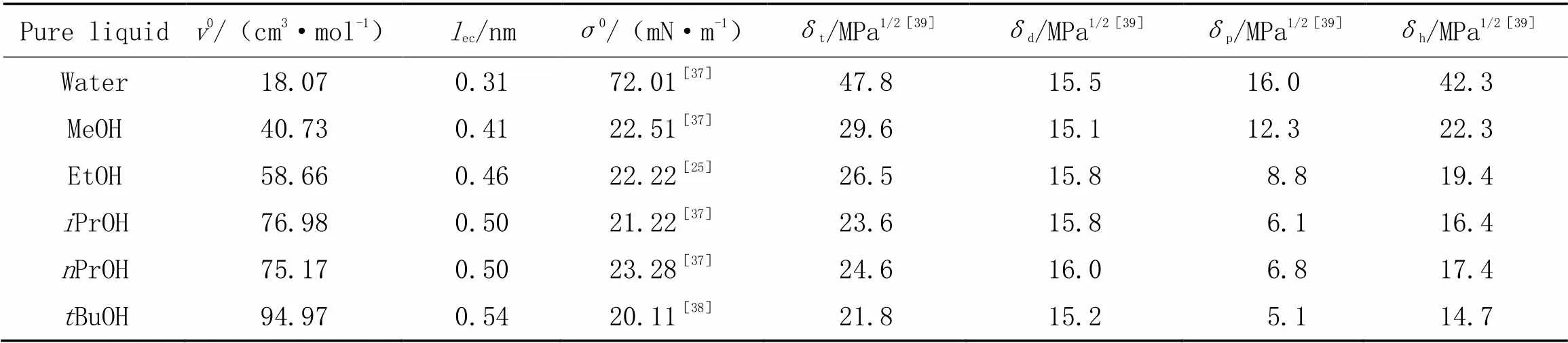
Table 1　Molar volumes, surface tensions, and solubility parameters of pure liquids

2.1　表面聚集吸附平衡

图1（A）和（B）分别为水（1）-短链醇（2）混合物的和r随2，b的变化， 其中数据引自文献［25，37，38］. 可以看出， 各体系均为LI型等温线［23］， 表明短链醇在混合溶液表面发生正吸附. 甲醇、 乙醇、 异丙醇和正丙醇体系的线依次降低，r线依次增高， 表明其界面活性（或吸附趋势）依次增强. 叔丁醇和正丙醇体系的等温线相近， 表明二者界面活性相近.r随2，b增大先急剧升高后趋于平缓， 甲醇、 乙醇、 异丙醇、 正丙醇和叔丁醇体系其转折点对应的2，b分别约为0.3， 0.2， 0.15， 0.1和0.1. Raina等［9］采用质谱测定了甲醇、 乙醇和正丙醇水溶液2，s随2，b的变化， 其等温线依次增高； 另外， 将2，s-2，b曲线的转折点视为“吸附饱和”（相应2，s分别约为0.65， 0.65和0.85）， 其对应的2，b分别约为0.3， 0.2和0.1. 本文模型预测结果与之一致.

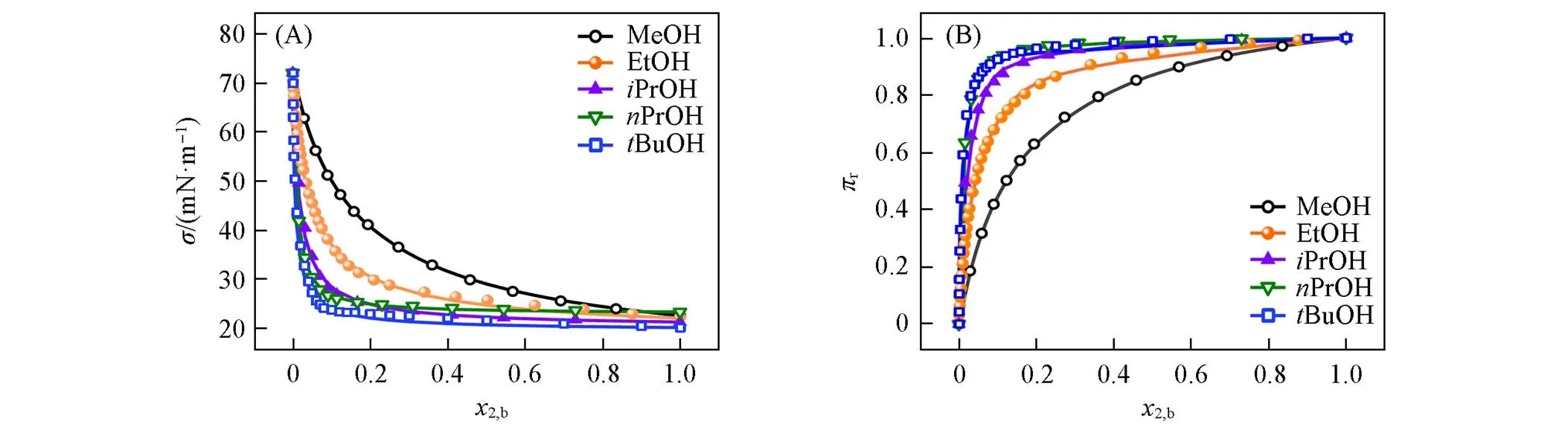
Fig.1　Change of surface tension(σ)(A) and reduced surface pressure(πr)(B) with bulk composition(x2,b) for water(1)⁃alcohol(2) mixtures

The symbols represent the experimental data， and the solid lines represent the model predictions.

采用式（9）对水（1）-短链醇（2）体系的π-2，b数据进行了线性拟合. 作为示例， 图2（A）和（B）分别 给出了甲醇和叔丁醇体系的拟合结果（其它3个体系的结果见本文支持信息图S1）， 可见， lg［r（1‒2，b）/（1‒r）］与lg2，b呈良好的线性关系， 与SAA模型预测一致. 需说明的是， 叔丁醇体系（还有乙醇和正丙醇体系）在高2，b区出现偏离， 可能是假设各物种活度系数为1所致［23，34］. 表2列出了各体系所得，K和值， 其=0.89～1.06（即≈ 1）， 表明短链醇在表面相无明显聚集［23］.

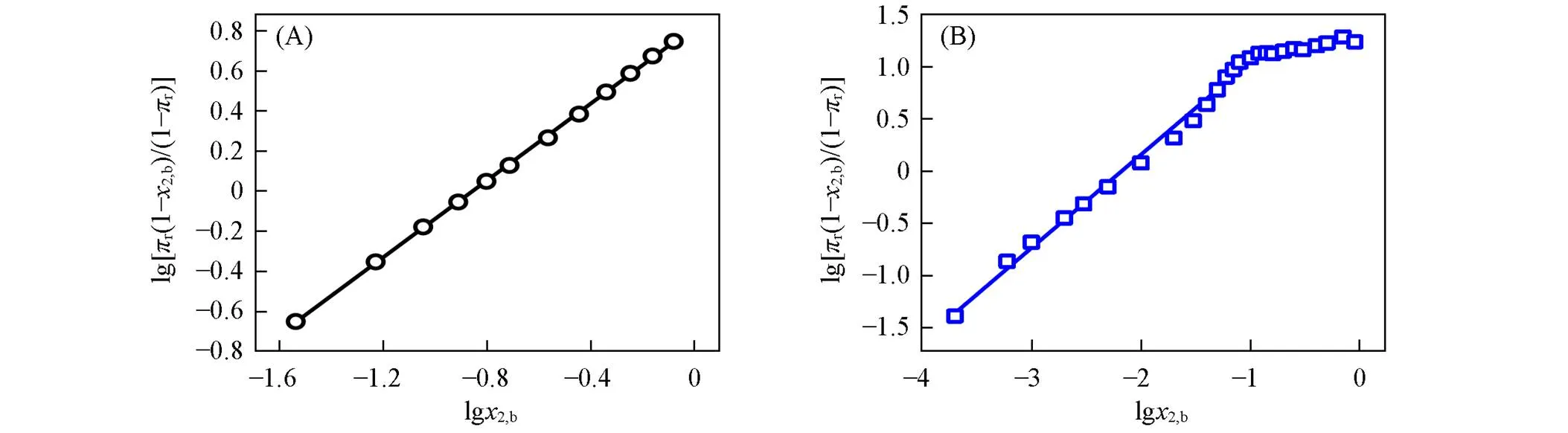
Fig.2　Linear fitting plots of Eq.(9) for πr⁃x2,b data of water⁃methanol(A) and water⁃tert⁃butanol mixtures(B)

The symbols represent the experimental data， and the solid line represents the model fitting.

Table 2　Model parameter values of water-alcohol mixtures

采用式（7）和式（8）及所得和K值计算了各体系的-2，b和r-2，b曲线， 示于图1. 可以看出， 模 型预测与实验数据间具良好的符合度， 其中甲醇、 乙醇、 异丙醇、 正丙醇和叔丁醇体系计算值的ARD分别约为0.2%， 1.0%， 1.7%， 1.1%和2.6%， 其AAD值分别为0.09， 0.32， 0.60， 0.30和0.80 mN/m. 这表明用式（7）及所得和K（或）值可准确描述-2，b曲线， 因而其和值可用于 式（12）和式（16）计算2和值.

液体混合物表面吸附趋势应由组分间的相互作用（或相似度）所决定. 二元液体混合物组分间的相互作用可用12表征［40］， 可由下式计算：

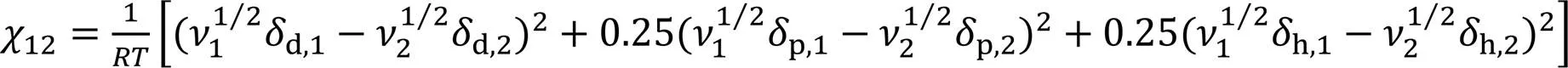
各体系的χ12值列于表2中， 可见甲醇、 乙醇、 异丙醇、 正丙醇和叔丁醇的χ12值有依次增大趋势. χ12值越大， 组分间的亲和力或相似度越低（即短 链醇的疏水性越强）， 越易发生表面 吸附.

2.2　Gibbs表面过剩

采用所建立的Gibbs代数方程（式12）计算了各体系2随2，b的变化， 由图4（A）可以看出， 各体系呈现相同的变化趋势. 随着2，b增大，2先急剧增大后逐渐 降低， 呈现一个最大值（记为2，max）， 与文献［17，36］报道一致.2，max值在4.77～5.60 μmol/m2间（表3）， 也与文献［7，36］报道值相近（若考虑活度系数，2，max值有所增大［7］）. 另外， 绘制了2-lg2，b图， 以清晰观察其2，max的位置［图4（B）］， 可以看出甲醇、 乙醇、 异丙醇、 正丙醇和叔丁醇体系的2，max所对应的2，b值（记为2b，mΓ）依次降低（表3）， 分别约为0.15， 0.05， 0.02， 0.01和0.006， 这与其吸附趋势依次增强一致. 对比图1（B）和图4（B）可看出，2，max时表面吸附未达饱和， 其相应表面相2，s值（记为2s，mΓ）也依次降低（表3）， 分别约为0.36， 0.26， 0.20， 0.20和0.17. Raina等［9］采用质谱测得甲醇在2，b=0.15时的2，s≈0.41， 乙醇在2，b=0.05时的2，s≈0.27， 正丙醇在2，b=0.01时的2，s≈0.2， 本文结果与其基本一致， 表明本模型预测数据是合理的. 下面分析影响2，max，2b，mΓ和2s，mΓ的主要因素.

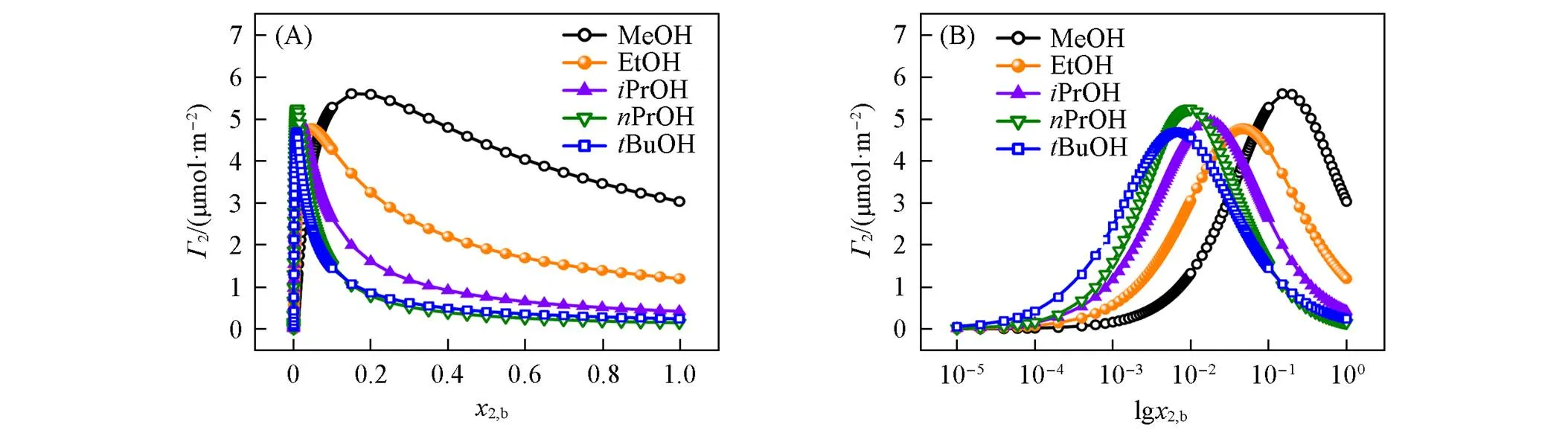
Fig.4　Change of Gibbs excesses(Γ2) with bulk composition(x2,b)(A) and its semi⁃logarithmic coordinate plots(B) for water⁃alcohol mixture

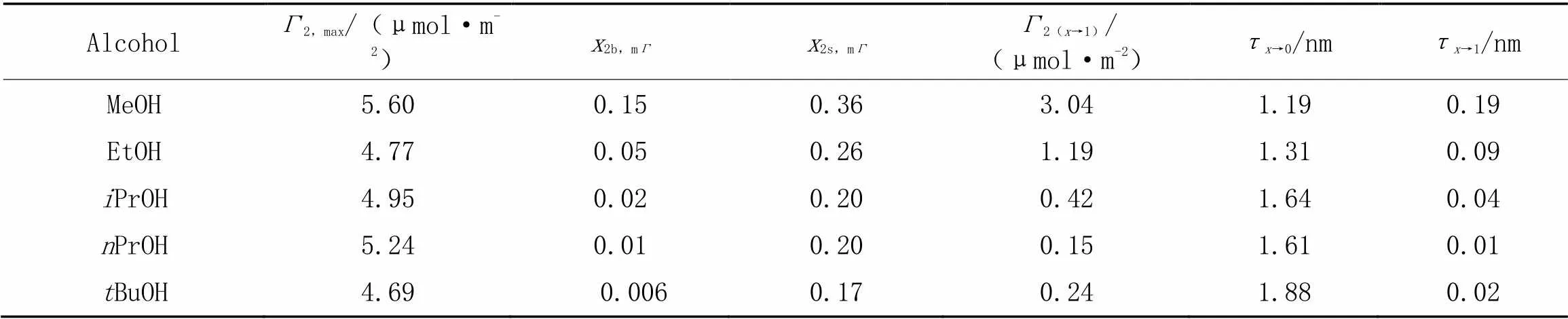
Table 3　Adsorption parameter values of water-alcohol mixtures

为了简便， 取=1， 由式（12）可得：

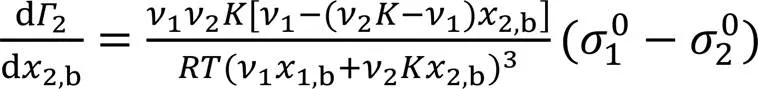
2为最大值时， d2/d2，b=0， 则

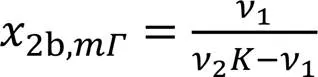
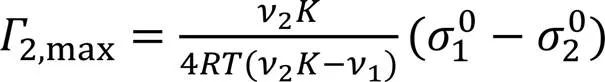
由式（2）和式（23）可得：

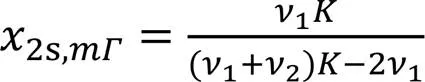
可以看出，和2越大，2b，mΓ和2s，mΓ均越小；2，max与2和（10-20）有关，2越大， （10-20）越小， 则2，max越大. 这可解释短链醇间2，max，2b，mΓ和2s，mΓ的变化［式（23）～式（25）计算值与所观察值可能略有差异， 因各体系的≠1］.

有趣的是， 从图4（B）还可看出， 甲醇、 乙醇、 异丙醇、 正丙醇和叔丁醇体系的2值在低2，b区呈依次增大趋势， 而在高2，b区与之相反； 当2，b→1时，2（x→1）也呈依次减小趋势（表3）， 与文献［36］报道 结果一致. 这些结果均由2值依次增大所致. 在高2，b区， 由式（14）可知，2增大，2减小. 另外， 由式（22）可知：

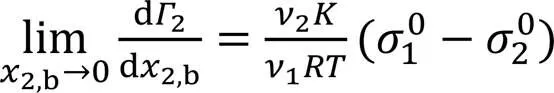
这表明在低2，b区，2值越大， 等温线极限斜率（d2/d2，b）→0越大， 故2越大.

需要说明的是， 采用多项式=∑aexp（‒bx2，b）拟合-2，b曲线， 其中a和b是拟合常数（令0=0）， 再采用Gibbs微分方程（式11）计算Г2值， 其结果与所建立的Gibbs代数方程（式12）结果基本一致（见本文支持信息图S2、 图S3及表S1）. 由以上讨论可知， 相较Gibbs微分方程， Gibbs代数方程可以提供更多的信息.

2.3　吸附层厚度

采用所建立的ALT方程（式16）计算了各体系随2，b的变化， 由图5（A）可以看出， 各体系呈现 相同的变化趋势. 对于给定的短链醇体系， 随着2，b增大，降低（呈指数衰减趋势）， 这与Li等［7］、 Azizian等［14］和Hyde等［8］（所研究水-乙醇体系）的结果一致. 有趣的是， 从-lg2，b图可以清晰看出， 在低2，b范围（lg2，b<0.001）内， 甲醇、 乙醇、 异丙醇、 正丙醇和叔丁醇体系的值依次增大， 而在高2，b区（lg2，b>0.02）依次减小［图5（B）］， 这与其极限（τ→0和τ→1）值变化一致（表3）. Bagheri等［13］和 Azizian等［14］研究了甲醇、 乙醇、 异丙醇、 正丙醇和正丁醇水溶液在低2，b范围内的值， 呈依次增大趋势， 本文结果与之一致. 由式（16）～式（18）可以看出， 在低2，b范围内（和τ→0）值的依次增大主要缘于醇分子尺寸（或2）的依次增大（因增大导致减小）， 而在高2，b范围内的依次减小可归因于吸附趋势的依次增强（值增大）.

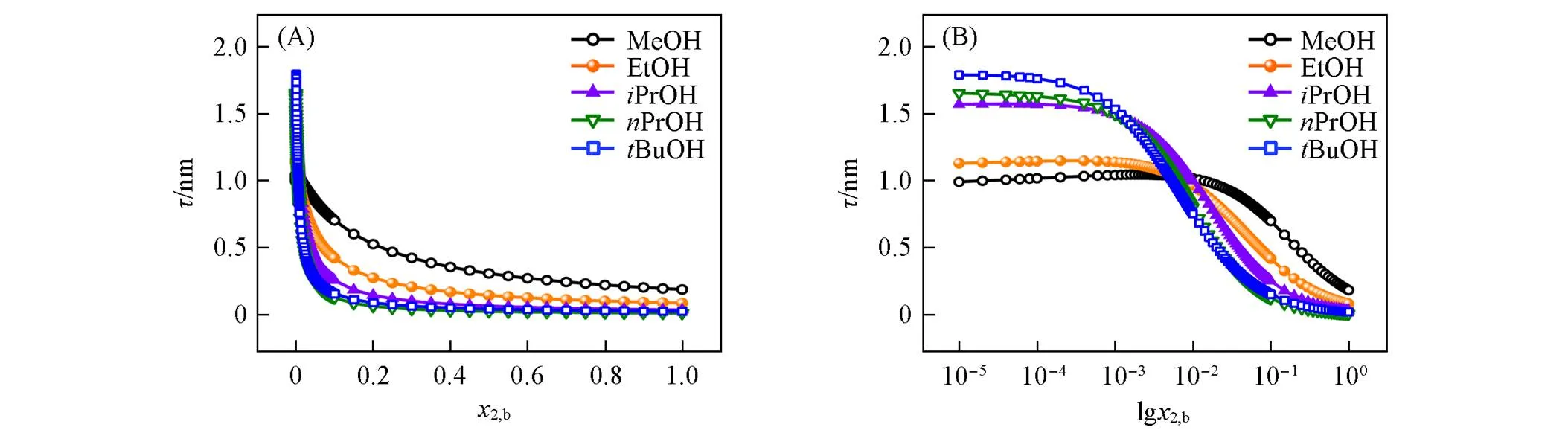
Fig.5　Change of surface adsorption layer thickness(τ) with bulk composition(x2,b)(A) and its semi⁃logarithmic coordinate plots(B) for water⁃alcohol mixtures

另外， 所研究短链醇体系的τ→0≈1.19～1.88 nm，τ→1≈0.01～0.19 nm， 其中τ→0结果与文献报道 值（甲醇： 1.2～1.7 nm［13，14］， 乙醇： 1.3～1.5 nm［8，13］， 异丙醇： 1.85 nm［13］）相近. Li等［7］采用中子反射 测得水-乙醇体系在2，b=0.022， 0.045和0.10时的值分别约为0.6， 0.52和（0.46±0.03） nm， 本文 结果（分别约为0.81， 0.47和0.42 nm）与之基本一致. 所得τ→1值很小， 缘于小的2（x→1）值［实际上τ→1≈22（x→1）］.

需说明的是， 模型预测的τ→0和τ→1值不是纯组分1和纯组分2的表面层厚度（纯液体表面层一般由1～3个分子层形成［6］）， 而是Gibbs过剩层厚度的极限值， 可视为模型特征参数值， 反映吸附趋势强弱（极限值越小， 吸附趋势越强）. 纯液体表面层单层厚度可用液体分子等当立方体边长（ec）表征［6］， 其值列于表1中. 据极限值和溶质ec值可推算溶质的吸附分子层数（2=/ec）. 甲醇、 乙醇、 异丙醇、 正丙醇和叔丁醇体系的2（x→0）分别约为2.9， 2.9， 3.3， 3.2和3.5， 其2（x→1）值分别约为0.46， 0.19， 0.07， 0.02和0.04.2（x→0）值的相对变化率较小（各体系可视为基本相近， 即2（x→0）=3.2±0.3）， 而2（x→1）值的相对变化较大， 表明前者可能主要由水（溶剂）的性质决定， 而后者可能与短链醇（溶质）性质有关（如表面分子排布形态等）， 这还有待进一步研究. 另外， 聚集体吸附不等同于多层吸附， 当2>1时可视为溶质发生多层吸附.

总之， 所建立的ALT模型方程可合理预测吸附层厚度随体相组成的变化， 吸附层厚度由吸附趋势和分子尺寸所决定.

3 结 论

基于SAA模型和Gibbs微分方程， 建立了Gibbs表面过剩（2）和表面过剩层厚度（）代数方程， 其优点是采用SAA模型参数（和）可在全浓度范围（2，b=0～1）内计算2和值. 甲醇、 乙醇、 异丙醇、 正丙醇和叔丁醇在水表面的吸附趋势依次增强， 与其疏水性依次增强趋势一致； 在低2，b区， 其2值和值均依次增大， 而在高2，b区均依次减小.值越大，值越小. 在低2，b区，2值的增大由和2依次增大所致， 而值的增大主要由2增大所致； 在高2，b区，2值的减小主要缘于2的依次增大， 而值的减小主要由值增大所致. 对于给定的短链醇体系， 随着2，b的增大，2先急剧增大后降低， 呈现一个最大值， 而其持续降低. 本研究加深了对水-短链醇液体混合物表面吸附行为的认识.

支持信息见http://www.cjcu.jlu.edu.cn/CN/10.7503/cjcu20230316.

［1］ Marmur A.，， 2017，， 164—173

［2］ Kaptay G.，， 2020，， 102212

［3］ Stephan S.， Hasse H.，， 2020，， 319—349

［4］ Vegh A.， Korozs J.， Kaptay G.，， 2022，， 4906—4912

［5］ Privat M.， Bennes R.， Tronel⁃Peyroz E.，， 1988，， 198—207

［6］ Douillard J. M.，， 2009，， 307—310

［7］ Li Z. X.， Lu J. R.， Styrkas D. A.， Thomas R. K.， Rennie A. R.， Penfold J.，， 1993，， 925—939

［8］ Hyde A. E.， Ohshio M.， Nguyen C. V.， Yusa S. I.， Yamada N. L.， Phan C. M.，， 2019，， 111005

［9］ Raina G.， Kulkarni G. U.， Rao C. N. R.，， 2001，， 10204—10207

［10］ Chen H.， Gan W.， Lu R.， Guo Y.， Wang H. F.，， 2005，， 8064—8075

［11］ Kirmse K.， Morgner H.，， 2006，， 2193—2199

［12］ Rafati A. A.， Bagheri A.， Khanchi A. R.， Ghasemian E.， Najafi M.，， 2011，， 252—258

［13］ Bagheri A.， Fazli M.， Bakhshaei M.，， 2016，， 442—451

［14］ Azizian S.， Moghadam T. F.，， 2011，， 67—71

［15］ Santos M. S. C. S.， Reis J. C. R.，， 2018，， 419—428

［16］ Butler J. A. V.，， 1932，， 348—375

［17］ Guggenheim E. A.， Adam N. K.，， 1933，， 218—236

［18］ Eberhart J. G.，， 1966，， 1183—1186

［19］ Connors K. A.， Wright J. L.，， 1989，， 194—198

［20］ Laaksonen A.， Kulmala M.，， 1991，， 6745—6748

［21］ Wang Z. L.， Chen Z. X.，，1995，（2）， 191—195（王兆林， 陈钟秀. 高等学校化工学报， 1995，（2）， 191—195）

［22］ Piñeiro Á.， Brocos P.， Amigo A.， Gracia⁃Fadrique J.， Lemus M. G.，， 2001，， 4261—4266

［23］ Qi W.， Yu X.， Du N.， Hou W.，， 2023，， 507—518

［24］ Ross S.， Morrison I. D.，， 1983，， 121—134

［25］ Strey R.， Viisanen Y.， Aratono M.， Kratohvil J. P.， Yin Q.， Friberg S. E.，， 1999，， 9112—9116

［26］ Menger F. M.， Shi L.， Rizvi S. A. A.，， 2009，， 10380—10381

［27］ Santos M. S. C. S.， Reis J. C. R.，， 2021，， 21571—21578

［28］ Kaptay G.，， 2015，， 5796—5804

［29］ Kaptay G.，， 2019，， 10987—10992

［30］ Wilson G. M.，， 1964，， 127—130

［31］ Brocos P.， Piñeiro Á.， Amigo A.， Gracia⁃Fadrique J.，， 2007，， 343—353

［32］ Santos M. S. C. S.， Reis J. C. R.，， 2019，， 525—535

［33］ Zhu B.， Gu T.，， 1991，， 1—32

［34］ Qi W. S.， Hou W. G.，， 2023，， 1236—1246（亓文帅， 侯万国. 中国科学， 2023，， 1236—1246）

［35］ Bermúdez⁃Salguero C.， Gracia⁃Fadrique J.，， 2015，， 10304—10315

［36］ Yano Y. F.，， 2005，， 255—259

［37］ Vázquez G.， Alvarez E.， Navaza J. M.，， 1995，（3）， 611—614

［38］ Gliński J.， Chavepeyer G.， Platten J. K.，， 1995，， 2113—2117

［39］ Hansen C. M.， Hansen Solubility Parameters⁃a User’s Handbook， CRC Press， Boca Raton， FL， 2007

［40］ Qin J.， Wang X.， Jiang Q.， Cao M.，， 2019，， 1069—1097

Surface Adsorption of Water-alcohol Binary Solutions

YUXianchao1， QIWenshuai1， DENGQuanhua2， HOUWanguo1，3*

（，，，，，250100，）

Algebraic equations of the Gibbs surface excess（2） and adsorption layer thickness（） were developed for binary liquid mixtures based on the surface aggregation adsorption（SAA） model and the Gibbs differential equation， which can predict the change of2andwith the bulk composition（such as the molar fraction of component 2，2，b） in the whole concentration range. The model equations were used to investigate the surface adsorption of water（1）-alcohol（2） binary solutions. The alcohols involved include methanol（MeOH）， ethanol（EtOH），-propanol（PrOH），-propanol（PrOH）， and-butanol（BuOH）. It was found that their adsorption trend on the water surface increases in turn， consistent with the enhancement trend of their hydrophobicity. Their2andincrease in turn in the low2，bregion， while decrease in turn in the high2，bregion， which arise from the differences in adsorption trend and molecular size between alcohols. In addition， for a given alcohol system， with an increase in2，bfrom 0 to 1， its2initially sharply increases and then decreases， showing a maximum， but itsexhibits a continuous reduction. This work provides a better understanding of the surface adsorption behavior of water-alcohol liquid mixtures.

Liquid mixture； Surface adsorption； Surface aggregation； Adsorption layer thickness； Thermodynamic model

2023-07-05

侯万国, 男, 博士, 教授, 主要从事胶体与界面化学研究. E-mail: wghou@sdu.edu.cn

国家自然科学基金(批准号: 22272088)资助.

O647

A

10.7503/cjcu20230316

2023-09-11.

Supported by the National Natural Science Foundation of China(No.22272088).

（Ed.： V， K， S）