例谈求解叠加电场的电场强度的策略

■安徽省庐江二中 吴 欣

以孤立点电荷为场源产生的电场是最简单的静电场,设场源电荷的电荷量为Q,则在其产生的电场中距离它为r处的电场强度。若场源不是单一点电荷,则求其产生电场的电场强度就需要一定的技巧。下面归纳求解叠加电场的电场强度的三种常见方法,供同学们参考。

一、矢量叠加法

若场源是多个点电荷,则电场中某点的电场强度等于各个点电荷单独在该点产生的电场强度的矢量和。若场源是一个比较大的不能视为点电荷的带电体,则可以采用微元法先将带电体分成足够小的若干小块,将每一小块视为点电荷,再用点电荷电场强度叠加法计算带电体产生电场的合场强。该方法适用于多个任意电场在空间某点产生电场的合场强的求解。

例1如图1 所示,真空中两个等量异种点电荷固定在水平方向上的A、B两点,相距为r,若正点电荷固定在A点,负点电荷固定在B点,两点电荷的电荷量大小均为Q,则下列判断中正确的是( )。

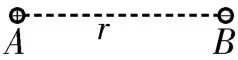
图1

A.两点电荷连线中点处的场强大小为0

C.与两点电荷相距均为r处的场强大小为,方向竖直向上

D.与两点电荷相距均为r处的场强大小为,方向水平向右

解析:如图2所示,设两点电荷在其连线中点M处产生的场强大小分别为E1和E2,方向均由正点电荷指向负点电荷,则,根据矢量叠加法得其连线中点处的合场强大小,方向水平向右,选项A 错误,B 正确。设两点电荷在与其相距均为r处P点产生的场强大小分别为E3和E4,两矢量的夹角为120°,则与两点电荷相距均为r处的合场强大小,方向平行于两点电荷连线,且由正点电荷指向负点电荷,即水平向右,选项C、D错误。

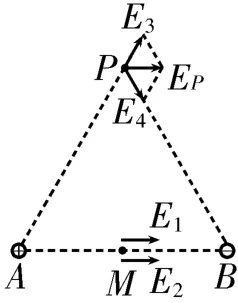
图2

答案:B

二、对称补偿法

若场源是非对称分布的不可视为点电荷的带电体A,直接求其产生电场的电场强度比较困难,则可以采用补偿法先将不对称的带电体A补上一个B,使其成为一个方便直接应用定理或公式进行求解的对称分布的带电体A+B,且补上的B也是方便求解的,这样带电体A产生电场的电场强度就等于带电体A+B与B产生电场的电场强度之差。

例2如图3所示,A、B、C、D、E、F是半径为r的圆周上等间距分布的六个点,在这六个点上各固定一个点电荷,其中A点处点电荷的电荷量为+q,其余五个点电荷的电荷量均为-q,则圆心O处的电场强度为( )。

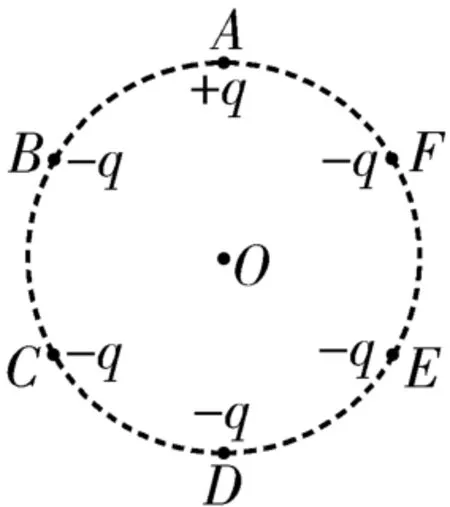
图3

解析:设想在A点处同时放一个电荷量为-q的点电荷和一个电荷量为+2q的点电荷,代替原来电荷量为+q的点电荷,这样圆周上对称分布的六个电荷量为-q的点电荷在圆心O处产生电场的合场强E1=0,电荷量为+2q的点电荷在圆心O处产生电场的场强大小,方向沿AO连线方向。根据矢量运算法则可知,题设六个点电荷在圆心O处产生的电场的场强大小,方向沿AO连线方向。

答案:D

点评:从对称性的角度分析物理过程,求解物理问题,往往可以避开冗长的数学求解过程,达到化繁为简、化难为易的目的。补偿法的本质就是通过巧妙补充,将不具有对称性的物理模型转化为两个具有对称性的物理模型,以便于一些物理定理或公式的直接应用。

三、极限特殊值法

若叠加电场的电场强度用常规方法难以直接求解,而利用极限法把某个物理量推向极端求得特殊值,则可以根据特殊值合理推断出一般结论。该方法一般适用于求解定性判断型选择题。

例3如图4所示,一半径为R的圆环上均匀地分布着电荷量为Q的电荷,在垂直于圆环平面的对称轴上有一点P,它与环心O之间的距离为L。已知静电力常量为k,下列关于P点的电场强度E的四个表达式中有一个是正确的。请你根据所学知识,通过分析判断这个正确的表达式是( )。

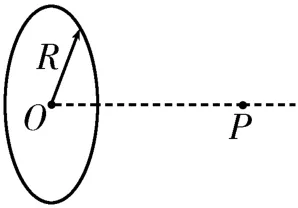
图4

解析:当R=0时,均匀带电圆环等同于一个所有电荷量集中于环心O的点电荷,根据孤立点电荷产生电场的电场强度计算公式可知,P点的电场强度大小。将R=0 代入四个选项进行验证,只有选项A、D 满足。当L=0时,P点与O点重合,均匀带电圆环产生的电场在环心O处的电场强度E=0。将L=0代入A、D 两选项进行验证,只有选项D 满足。

答案:D

点评:利用极限特殊值法求解叠加电场的电场强度时,需要先判断哪些量是可以推向极端的,再确定可以推向的极端是趋于零还是趋于无穷大。本题中将R、L推向极值零,得出P点的电场强度,分别代入四个选项即可判断哪个表达式是正确的。

跟踪训练

1.如图5所示,正方体的八个顶点处分别固定着电荷量为+q和-q的点电荷,正方体范围内电场强度为零的点分别是( )。

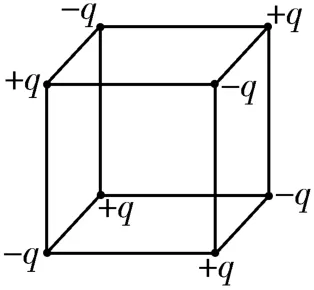
图5

A.体中心、各面中心和各边中点

B.体中心、各顶点和各边中点

C.体中心和各面中点

D.体中心和各边中心

2.一半径为R的半球面上均匀分布着电荷量为Q的正电荷,电荷Q在球心O处产生的电场的电场强度大小。把半球面分为表面积相等的上、下两部分,如图6甲所示,上、下两部分表面所带电荷在球心O处产生电场的电场强度大小分别为E1、E2;把半球面分为表面积相等的左、右两部分,如图6乙所示,左、右两部分表面所带电荷在球心O处产生电场的场强大小分别为E3、E4。下列判断正确的是( )。

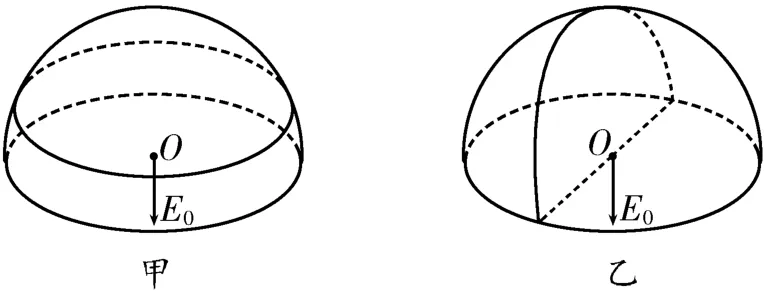
图6

3.如图7 所示,一个内、外半径分别为R1和R2的圆环状均匀带电平面,其单位面积带电荷量为q。取环面中心O为原点,以垂直于环面的轴线为x轴,设轴上任意点P到O点的距离为x,P点的电场强度大小为E,静电力常量为k。下列关于E的四个表达式中只有一个是合理的。请你根据所学知识,通过分析判断这个合理的表达式是( )。

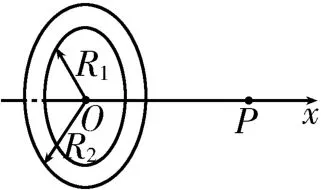
图7

参考答案:1.C 2.D 3.B