电磁感应现象中“杆+导轨”模型梳理

■河南省郑州市第三十一高级中学 董卫刚 王梦娜

电磁感应现象中的“杆+导轨”模型是近几年高考中的常见考点之一,比如2020年高考全国Ⅰ卷第21题、全国Ⅲ卷第24题,2021年高考全国乙卷第25 题、北京卷第7 题,2022年高考全国甲卷第20 题、辽宁卷第15题,2023年高考全国甲卷第25题、湖南卷第14题、辽宁卷第10 题等。涉及“杆+导轨”模型的物理试题几乎涵盖了高中物理所有的核心内容,综合性较强,区分度较高。下面将涉及“杆+导轨”模型的物理试题进行系统梳理,总结求解此类问题的思路和方法,为同学们的复习备考提供参考。

一、电磁感应核心知识梳理

1.感应电流方向的判断方法:

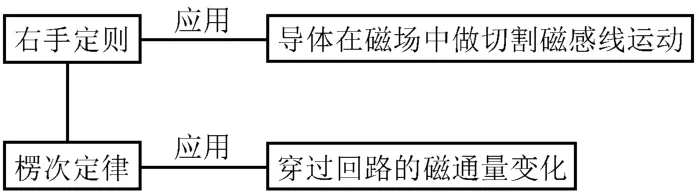
2.感应电动势大小的求法:

图1

图2

图3

3.感应电荷量的计算:

4.动量定理在“杆+导轨”模型中的应用:

二、“杆+导轨”模型梳理

模型一:单杆,无电源,受恒定外力

如图4 所示,金属杆MN放在水平放置的光滑导轨上,空间存在垂直于导轨平面向上的匀强磁场,金属杆MN受到恒定的外力作用。以金属杆MN为研究对象,根据牛顿第二定律得,解得,因此随着速度v的增大,加速度a逐渐减小,当a=0的时候,金属杆MN达到平衡状态,以恒定的速度做匀速直线运动。上述规律不仅适用于水平面内的运动,竖直平面内的运动或斜面上的运动也适用,只不过是将恒力稍微变化了一下。

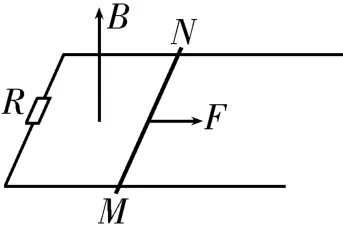
图4

例1如图5所示,两根足够长的光滑导轨竖直放置,间距为L,顶端接阻值为R的电阻。匀强磁场方向垂直于导轨所在平面(纸面)向里,磁感应强度为B,质量为m、电阻为r的金属棒在距磁场上边界某处由静止释放,金属棒和导轨始终接触良好。不计导轨的电阻,重力加速度为g,则下列说法中正确的是( )。

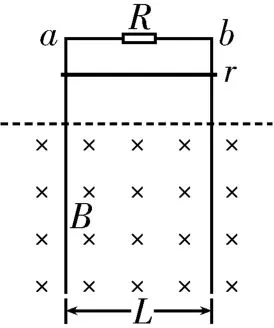
图5

A.金属棒在磁场中运动时,通过电阻R的电流方向为a→b

B.金属棒刚进入磁场时一定做加速运动

C.金属棒的速度为v时,金属棒所受的安培力大小为

D.金属棒以稳定的速度下滑时,电阻R的热功率为

思路点拨:金属棒进入磁场后,产生的感应电动势E=BLv,回路中的感应电流,通过电阻R的电流方向为b→a,金属棒所受的安培力大小,当金属棒稳定下滑时,F=mg,电阻R的热功率,解得。

答案:D

模型二:单杆,无电源,有初速度

如图6 所示,给金属杆ef一个初速度(初始冲量),让金属杆ef运动起来,金属杆ef切割磁感线,在回路cbef中产生感应电流,金属杆ef相当于电源,此时金属杆ef受到一个与运动方向相反的安培力,阻碍金属杆ef的运动,金属杆ef做减速运动,速度减小会让安培力随着减小,加速度就跟着减小,因此金属杆ef做加速度减小的减速运动,直到速度减为零,停止运动。若导轨是光滑的,则金属杆ef的初动能全部转化为电阻R产生的焦耳热,即,金属杆ef通过克服安培力做功把机械能转化为了电能。同时还可以根据动量定理得,又有q=·Δt,求出在此过程中通过电阻R的电荷量。

图6

例2(2021年高考北京卷)如图7所示,在竖直向下的匀强磁场中,水平U 型导体框左端连接一阻值为R的定值电阻,质量为m、电阻为r的导体棒ab置于导体框上。不计导体框的电阻、导体棒与框间的摩擦。导体棒以水平向右的初速度v0开始运动,最终停在导体框上。在此过程中( )。

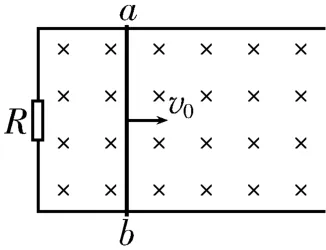
图7

A.导体棒做匀减速直线运动

B.导体棒中感应电流的方向为a→b

C.电阻R消耗的总电能为

思路点拨:导体棒做加速度减小的减速运动,导体棒中感应电流的方向为b→a。安培力的变化会引起加速度的变化,根据能量守恒定律和动能定理可知,电阻R消耗的总电能为,导体棒克服安培力做的总功等于。

答案:C

模型三:单杆,有电容,受恒定外力

如图8所示,水平放置的光滑平行导轨左侧接电容为C的电容器,空间存在垂直于导轨平面向上的匀强磁场,金属棒MN和导轨的电阻忽略不计,摩擦力不计,金属棒MN在水平向右的恒定拉力F的作用下,由静止开始做加速运动,持续对电容器充电,则存在充电电流时,有F-BIl=ma,,ΔQ=CΔU,ΔU=ΔE=BlΔv,整理得,其中,解得,因此金属棒MN做加速度恒定的匀加速直线运动。从能量的角度分析,存在功能关系。

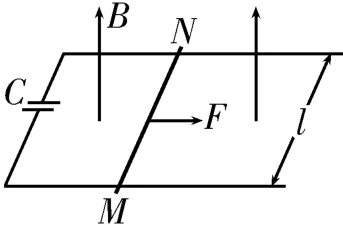
图8

例3如图9所示,间距为L的金属导轨竖直平行放置,空间存在垂直于导轨所在平面向里的匀强磁场,磁感应强度为B,在导轨上端接一电容为C的电容器,一质量为m的金属棒与导轨始终保持良好接触。将金属棒距地面高度为h处由静止开始释放,已知重力加速度为g,一切摩擦及电阻均不计。在金属棒下滑至地面的过程中,下列说法正确的是( )。

图9

A.若h足够大,则金属棒最终匀速下落

B.金属棒下滑至地面时,电容器储存的电势能为mgh

思路点拨:根据牛顿第二定律得mg-BIL=ma,又有,v=at,Q=It,解得,金属棒在下降过程中做匀加速直线运动,金属棒下滑至地面时的动能,又有,根据能量守恒定律得电容器储存的电势能。

答案:D

模型四:双杆,等长,有初速度

如图10所示,光滑导轨上放置两根导体棒,给导体棒1 一个初速度,导体棒1受安培力的作用做加速度减小的减速运动,导体棒2受安培力的作用做加速度减小的加速运动,最后两导体棒以相同的速度做匀速直线运动,对两导体棒运用动量守恒定律可以求出最终的共同速度。从能量的角度分析,导体棒1动能的减少量=导体棒2 动能的增加量+焦耳热。

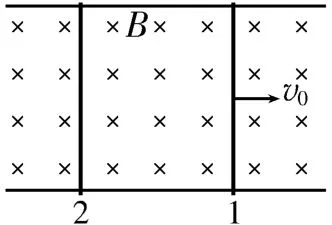
图10

例4如图11所示,两根足够长的平行光滑导轨固定在绝缘水平面上,所在空间存在方向垂直于水平面、磁感应强度为B、范围足够大的匀强磁场,导轨的间距为L,电阻不计;导轨上静置两根有效长度均为L的导体棒PQ和MN,其中导体棒PQ的质量为2m、阻值为R,导体棒MN的质量为m、阻值为2R。若在t=0 时刻给导体棒PQ一个平行于导轨向右的初速度v0,不计运动过程中两导体棒的相互作用,则( )。

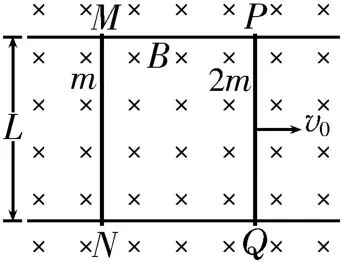
图11

A.t=0 时刻,两导体棒的加速度大小相等

B.t=0时刻,导体棒PQ两端的电压为

C.导体棒PQ匀速运动时的速率为

D.从t=0时刻到导体棒PQ匀速运动的过程中,导体棒MN中产生的焦耳热为

思路点拨:导体棒PQ向右运动,产生的感应电动势E=BLv0,此时路端电压为,回路中的感应电流,两导体棒受到的安培力大小均为F=BIL,则,因此t=0 时刻,两导体棒的加速度大小不相等,受到的安培力大小相等,方向相反,两导体棒在运动过程中满足动量守恒定律,则2mv0=(m+2m)v共,最终两导体棒以速度做匀速直线运动。两导体棒中的电流相等,产生的焦耳热分别为,则QMN∶QPQ=2∶1。根据能量守恒定律可知,在整个运动过程中产生的总热量等于系统总动能的减少量,即,解得。

答案:BD

模型五:双杆,等长,受恒定外力

如图12所示,足够长的光滑导轨上放置两根导体棒,导体棒1 受到一个恒定的力F的作用,导体棒1 做加速度逐渐减小的加速运动,导体棒2做加速度逐渐增大的加速运动,最终两导体棒以相同的加速度做匀加速直线运动,两导体棒的速度差恒定,回路中存在恒定的感应电流,两导体棒受到的安培力大小相等,对整体有F= (m1+m2)a,对导体棒2 有,联立以上两式可以求出两导体棒的速度差值。从能量的角度分析,外力做的功=导体棒1的动能+导体棒2的动能+焦耳热。

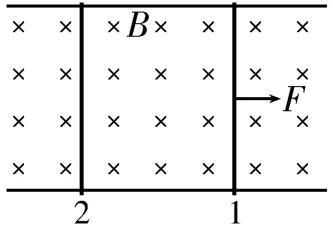
图12

例5(2020年高考全国Ⅰ卷)如图13所示,U 型光滑金属框abcd置于水平绝缘平台上,ab边和dc边平行,和bc边垂直。ab、dc边足够长,整个金属框的电阻可忽略。一根具有一定电阻的导体棒MN置于金属框上,用水平恒力F向右拉动金属框,运动过程中,装置始终处于竖直向下的匀强磁场中,导体棒与金属框保持良好接触,且与bc边保持平行。经过一段时间后( )。

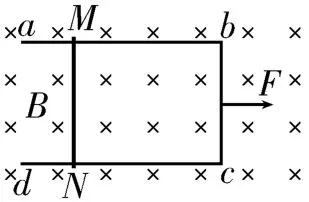
图13

A.金属框的速度大小趋于恒定值

B.金属框的加速度大小趋于恒定值

C.导体棒所受安培力的大小趋于恒定值

D.导体棒到金属框bc边的距离趋于恒定值

思路点拨:金属框向右的加速度与导体棒的加速度不同,同一时刻两者速度也不同,设金属框的质量为m1,速度为v1,导体棒的质量为m2,速度为v2,则回路中的感应电流,感应电流从0 开始增大,导体棒的加速度a2从零开始增大,金属框的加速度a1从开始减小,二者的加速度差值减小,当a1=a2时,有F=(m1+m2)a,则恒定,根据F安=m2a可知,安培力不再变化,感应电流不再变化,金属框与导体棒的速度差保持不变,但导体棒的速度小于金属框的速度,则导体棒到金属框bc边的距离越来越大。

答案:BC

模型六:双杆,不等长,有初速度

如图14 所示,光滑导轨水平放置,匀强磁场垂直于水平面向下,左侧导轨间距为L,右侧导轨间距为2L,且两侧导轨均足够长。现给金属杆cd一水平向右的初速度v0,金属杆cd做切割磁感线运动,产生感应电流,金属杆cd受到的安培力阻碍它的运动,金属杆ab受到的安培力使它做加速运动,两金属杆长度不同,所受安培力大小不相等,系统动量不守恒,一旦金属杆ab开始运动,金属杆ab也要做切割磁感线运动,产生一个反电动势,使得回路中的感应电流减小,当感应电流为零时,两金属杆均做匀速运动,此时两金属杆的速度关系为vab=2vcd,分别对两金属杆应用动量定理可以求出最终的速度。

图14

例6如图15所示,光滑导轨水平放置,匀强磁场垂直于水平面向下,磁感应强度为B,左侧导轨间距为L,右侧导轨间距为2L,且两侧导轨均足够长。质量为m的导体棒ab和质量为2m的导体棒cd均垂直于导轨放置,处于静止状态。导体棒ab接入电路的电阻为R,导体棒cd接入电路的电阻为2R,两导体棒始终在对应的导轨部分上运动,并始终与导轨垂直且接触良好, 导轨电阻不计。现瞬间给导体棒cd一水平向右的初速度v0,则对此后的运动过程,下列说法中正确的是( )。

图15

A.两导体棒组成的系统动量守恒

B.导体棒cd最终的速度为

C.整个过程中,通过导体棒cd的电荷量为

D.从导体棒cd获得初速度到二者稳定运动的过程中,系统产生的焦耳热为

思路点拨:因为导体棒ab和cd的长度不同,所以受到的安培力大小不相等,两导体棒组成的系统动量不守恒。当导体棒ab和cd产生的感应电动势大小相等时,两导体棒都做匀速直线运动,则BLvab=B·2Lvcd,对两导体棒分别应用动量定理得,解得。结合,解得。根据能量守恒定律得整个过程中系统产生的焦耳热,解得。

答案:CD

总结:“杆+导轨”是一个经典的模型,涉及知识点比较多。在以“杆+导轨”模型为素材的电磁感应问题中,若满足动量守恒条件,则应优先选用动量守恒定律列式求解;若已知位移,则需结合动能定理列式求解;若已知时间,则需结合动量定理列式求解;若需要求电荷量,则需要应用安培力的冲量I安=BLq,并结合能量守恒定律列式求解。总之,求解以“杆+导轨”模型为素材的电磁感应问题时,需要充分挖掘题目隐含条件,使复杂的问题简单化,将难点逐个突破。