多虚拟电厂日前随机博弈与实时变时间尺度优化方法

葛晓琳，曹旭丹，李佾玲

（上海电力大学 电气工程学院，上海 200090）

0 引言

虚拟电厂（virtual power plant，VPP）是通过自身运营控制中心对多种分布式电源（distributed energy resource，DER）、储能单元及可控负荷进行整合，所形成的可被常态化调度的特殊电厂［1］。VPP是新型电力系统中用电终端能效管理的关键载体。在VPP 发展的过程中，其内部高比例的DER 使得单个VPP 参与电网调度时灵活性不高，面临着较大的收益损失风险。而不同VPP 中包含的DER 具有互补性，可通过多VPP的协同优化实现资源互济，进而提升VPP 运行的整体效益。因此，多VPP 的协同优化运行与交易已成为目前的研究热点［2］。然而，多VPP内部包含了难以预测的高比例风、光随机电源，外部需要考虑跨地域的功率调配，协同运行与交易难度大。

针对多VPP 的优化中风、光出力不确定性带来的风险，文献［3］考虑不确定性带来的收益风险，基于条件风险价值理论，提出了VPP 日前优化运行模型。文献［4］考虑电能不足期望与VPP 可调度容量的关系，为VPP 的经济性与风险平衡调度奠定了基础。文献［5］分析了不同场景、置信水平、风险系数下VPP 的风险水平，探讨了VPP 运行风险与经济性的平衡点。文献［6］基于条件风险价值与置信度理论，建立了能够描述VPP风险的模型，为决策者提供了决策参考。在上述文献中，风险测度指标的权值为给定的风险系数，且针对可中断负荷、储能等元件对VPP整体风险水平的影响研究不足。

针对多主体VPP的互动优化，文献［7］设计了非完全信息条件下的日前优化调度场景，针对多主体互动优化关系，采用贝叶斯博弈理论建立了VPP 多主体协同优化模型。文献［8］构建了考虑多主体利益的多VPP 系统主从博弈优化运行模型，对VPP 进行了分布控制、协同优化。文献［9］将多主体的经济性和协同运行描述为机组组合问题，描述了多主体能源交易组合的离散特性，构建了基于两阶段自适应鲁棒的多主体协同运行模型。文献［10］构建了多VPP 非合作动态博弈日前市场优化交易模型，模拟了其他主体对自身决策的影响，制定了最优交易策略。但上述文献大多借鉴微电网调度的方法对VPP进行优化，并未考虑多VPP之间的跨地域特性，且关于过网费的承担机制也并未进行详细分析。

此外，在减小预测信息不确定的影响方面，多时间尺度滚动优化被广泛认可与采用，其中文献［11］提出了一种基于需求响应和博弈论的多VPP交互式调度模型，形成日前-日内-实时多时间尺度滚动调度策略。文献［12］充分考虑了资源调度灵活性，在日前-日内2 个时间尺度制定资源调整优先级，提高了系统运营经济性。文献［13］分析了直流配电网各电压等级特点，构建了分层、多时间尺度滚动优化模型，实现了系统的低成本优化。文献［14］提出了一种双层多时间尺度协同优化方法，研究了预测信息和随机组件故障的不确定性对电力平衡、运行成本和系统可靠性的影响。然而现有研究多以固定时间尺度分度值进行调度策略制定，但预测偏差大小具有随机性，如何灵活设置调度时间尺度仍需进一步研究。

综上，本文提出了多VPP 日前随机博弈与实时变时间尺度协同优化方法。首先，针对VPP 在日前风光发电出力及负荷需求预测不确定性，定义风险效用水平衡量VPP 对风险的偏好程度。进而，在此基础上考虑网络相关约束、VPP 直接交易报价动态约束等对VPP的日前电能交易进行了风险调度。然后，在日前计划确定的基础上，对实时调节时间尺度进行自适应改变，协调优化了调节成本与调度偏差。最后，结合仿真算例验证了所提策略的有效性。

1 多VPP 日前随机博弈与实时变时间尺度协同优化框架

本文所研究的VPP 同时包含发电和用电单元，在一段时间内可以在市场中出售或购买电量。结合目前电力市场发展处于初步阶段的实际情况，本文的研究主要着眼于发掘VPP间直接电能交易的可能性，充分挖掘其潜力，在配合电网完成系统调节的同时实现自身的收益最优。为了简化问题，VPP 与主网交易时的角色仍是“价格接受者”，即VPP 与主网交易的购售电价由政府定价［15］。

在日前阶段，为便于统计交易量，假定每个VPP通过统一关口节点与主网相连，在日前市场开始前，考虑不确定风险因素、网络约束及过网费分摊机制，有线路相连的VPP 之间进行议价议量，决策变量为各时段VPP 间的交易电量和交易价格、VPP 内部需求响应资源的调度量。电量优先在VPP之间交流结算，若所有售电型VPP 或购电型VPP 经过内部响应和外部直接交易后仍不满足公共耦合点（point of common coupling，PCC）的需求，则相应出现缺额的VPP 需要通过惩罚机制进行平衡，即售电型VPP 的售电余量按照低于正常VPP与主网交易电价进行结算，购电型VPP的购电差额部分则按合约进行罚款。不直接相连的VPP 则跳过VPP 之间议价议量的博弈，只能靠内部响应与在惩罚机制下和主网进行议价不议量的电能交易满足PCC 需求。此外，VPP 在追求自身利益的最大化的同时，除了对内表现为能量管理者外，对外必须对电网表现出作为电厂的外特性，即有既定的发电出力要求，因此，VPP 日前确定的交互计划在上报后不可更改。

在实时阶段，将日前优化中得到的交互功率作为实时滚动优化中交互功率初始值，结合实时更新的预测信息对VPP 的内部可调节单元进行动态调整。此阶段参与调整的是有调节余量的可中断负荷和储能单元。采用较小时间分度值能够获得更优的调度效果，但频繁进行信息更新和调度，通常调度成本会提高；采用更大的时间分度值可能调度成本较低，但对不确定性的处理效果往往不够理想。因此，选择合适的调度时间分度值至关重要，为兼顾减小预测信息不确定性影响与控制VPP 调节成本，提出实时调节时间尺度自适应变化的优化模型。

多VPP日前随机博弈与实时变时间尺度协同优化方法的总体流程图如附录A图A1所示。

2 VPP日前电能交易模型

2.1 不确定性分析

本文所研究的VPP 组成元件包括风电、光伏机组、常规不可控负荷、可中断负荷、储能单元。受天气条件的影响，风电、光伏出力具有随机性，加之存在预测不准确的情况，日前可再生能源出力预测、负荷预测存在偏差。

为应对日前预测信息的不确定性，采用条件风险价值度量风险，并引入效用理论，通过对不可调节单元和可调节单元的效用函数分别进行求解，将二者结合得到能够动态衡量VPP对外表现的整体风险偏好程度的时变参数，以此作为日前随机博弈的依据。

2.1.1 效用理论

效用理论是一种用于分析决策者对待风险的态度的理论。效用值是一个无量纲的相对指标，一般规定取值范围为［0，1］，效用值为0 代表决策者最不喜好、最想规避的事物，效用值为1 代表决策者最喜好、最倾向的事物。效用值的作用在于将有质的差别却难以量化的事物加以量化［16］。

将VPP中风电、光伏机组、常规不可控负荷统称为不可调节单元，认为其对预测偏差表现为风险规避性。同时将可中断负荷、储能单元统称为可调节单元，由于其能够通过自身调节产生获利行为，故认为其对不可调节单元的预测偏差表现为风险偏好性。对于不可调节单元，选用风险厌恶效用函数衡量；对于可调节单元，选用风险喜好效用函数进行衡量。本文中选用的是常用的风险规避型和风险喜好型效用函数形式［17］。设U(f)为效用函数，f为各类对象对风险的适应函数，本文规定效用值取值范围为［0，1］。并认为不可调节单元的预测误差服从均值为0、方差为的相互独立正态分布。

对于不可调节单元，当预测偏差最小时，对应风险适应函数取值为1，此时效用值最高，取值为1，将上述特殊值代入可求得待定参数cavo=1-exp(-1)。

2.1.2 风险效用水平

综合考虑可调节单元与不可调节单元的效用函数，进一步将其整合得到整个VPP 的风险效用水平ζ，ζ∈[0，1]，其反映了在95 % 置信水平下，VPP 对外表现的整体风险偏好程度，其值越大代表该VPP 对风险的“接受度”越高。t时段第i个VPP（VPPi）的风险效用水平表达式为：

2.2 优化目标

作为独立的理性个体，各VPP 均希望通过谈判达成共识，寻求最大限度地提升各参与主体收益的最优策略。因此，确定VPP 之间直接电能交易的交易电量和交易价格，是所有参与主体关注的重点。纳什谈判理论属于合作博弈范畴，可兼顾个体和集体利益，其均衡解可使各博弈参与者均获得Pareto最优效益，对多主体合作与竞争并存的决策优化问题具有适用性［18］。优化目标函数如式（6）所示。

式中：N为参与谈判主体总数；Ui为参与谈判主体i的效益；UN，*i为谈判破裂点，即VPP 不参与直接交易时的效益，其意义代表VPP 参与直接交易收益低于独立运行时，VPP退出合作联盟。

综合考虑VPP个体在各时段的经济性目标与对风险的偏好程度，建立VPP 考虑风险水平的效益模型，如式（7）所示。

2.3 日前阶段的约束条件

2.3.1 网络相关约束

1）网络关联约束。

本文假设VPP 除与主网交易外，还可与和自身相连的其他VPP进行直接交易。VPP之间的直接交易是指VPP之间不需要经过电压变换直接进行功率的交互。一旦涉及VPP 之间的直接交易，则必须要考虑VPP 之间的实际物理连接。不同网络结构下VPP 电能交易示意图如图1 所示。以VPP4向VPP1输送电能为例：在各VPP 之间均存在物理连接的情况下，VPP1与VPP4可以优先通过已有物理连接进行直接交易而无须升压后通过主网进行交易，如图1（a）所示；在VPP4与其他VPP 之间没有物理连接的情况下，倘若二者要发生交易，则必须要升压后通过主网进行，无法进行直接交易，如图1（b）所示。

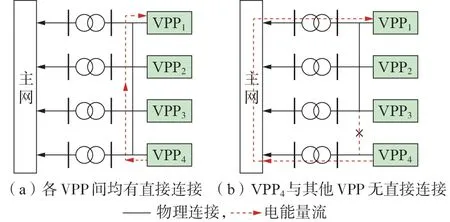
图1 不同网络结构下VPP电能交易示意图Fig.1 Schematic diagram of VPP power trading under different network structures

构建网络关联矩阵E，有物理连接的VPP 间相关性为1，无物理连接的VPP间相关性为0，令：

式中：pline，max为VPPi至VPPj间线路的最大注入有功功率；Δt为时间间隔。

2.3.2 交易电量约束

为防止VPP倒卖行为，规定在同一时段，VPP只具有售电或购电中的1 种权限，不会同时从电价低的一方购电并转卖给电价高的一方，交易电量约束如式（14）、（15）所示。

2.3.3 交易电价动态约束

考虑到交易电价与过网费的耦合关系，各VPP直接交易的报价应满足如下动态约束，其中式（16）、（18）、（20）为售电报价约束，式（17）、（19）、（21）为购电报价约束。

1）过网费由购、售电双方均摊时应满足的动态约束为：

此外，模型还需满足供需平衡约束、可中断负荷约束、储能约束，表达式见附录A式（A5）—（A14）。

3 VPP实时变时间尺度优化模型

3.1 实时阶段的优化目标

为了应对VPP内不可调节单元预测信息的更新和波动，满足VPP的对外出力要求，实时阶段以VPP对外交互电量与日前上报曲线偏差最小和VPP调度附加成本最小为目标，对VPP 内部可快速响应的有调节余量的可中断负荷资源和储能单元进行二次调整。

1）目标1：VPP对外交互电量与日前上报曲线偏差最小。

2）目标2：VPP调度附加成本最小。

在此阶段，VPP 的调度附加成本包括可调节负荷与储能单元的调度成本、偏差惩罚成本。目标函数为：

时间尺度分度值是否进行调整的关键在于偏差与调度成本之间的博弈。根据实时阶段更新信息计算出以基础时间尺度进行调度的调度成本与调度后偏差，若小于设定阈值，则以基础时间分度进行调度；若偏差大于设定阈值，则缩小调度时间分度值，重新计算以缩小时间尺度进行调度后的调度成本与调度后偏差，并比较偏差减少率与调度成本增加率之间的关系，当偏差减少率大于成本增加率时，对调度时间尺度进行更新，否则维持原调度时间分度值。

3.2 实时阶段的约束条件

各时间尺度的关系如附录A 图A2 所示。此阶段需要满足时间尺度约束，如式（26）所示。

考虑到实时市场在固定时段进行结算的规则，定义实时调度基础时间尺度TR=15 min，w=3，缩小时间尺度Tr=5 min。即规定调度指令间隔在15 min和5 min 中进行选择，无论何种时间尺度进行调度，改变的是基础时间尺度内调度计划调整次数，而结算时间间隔始终保持15 min。此外，在实时调整阶段同样需满足可中断负荷约束与储能单元约束。

综上，本文构建了日前-实时两阶段配合的多VPP 的电能交易与变时间尺度优化模型。在日前阶段，将式（7）代入式（6）得到非凸非线性优化问题，附录B 中根据均值不等式对其进行转化［19］，对得到的2 个子问题依次求解得到日前上报曲线并将其传递到实时调度阶段。在实时调度的每个时段开始前，需对VPP 进行状态滚动更新传递，在此基础上运用归一化和线性加权将多目标转化为单目标［20］，求解制定下一时段的调度时间尺度和调度策略。

4 算例分析

4.1 算例说明

为验证本文所提优化策略的有效性，以附录C图C1 所示VPP-主网联合系统结构为例，对所提优化策略进行了仿真分析。

规定VPP 间连接的输电线路最大传输容量为250 kW。各VPP 内包含分布式光伏、风电、常规负荷这3 种不可调节单元，包含可中断负荷、储能这2 种可调节单元。设风、光日前预测出力波动方差为0.02，负荷预测波动方差为0.002，风、光发电出力、负荷用电预测数据如附录C 图C2 所示，电网分时电价如附录C表C1所示。

4.2 仿真结果分析

4.2.1 VPP合作运行电能交易分析

依次求解日前阶段VPP 合作运行电能交易问题经过转化后得到的2 个子问题，所需总时间为22.16 s。VPP 在进行直接交易后的总收益高于合作运行前总收益的13.005 %，其中各VPP 的个体收益也均获得了普遍提升，具体数据如附录C表C2所示。

议价交易的电能价格在各时段均高于电网公司的回购电价，低于电网公司的销售电价，具体可见附录C 图C3。即售电VPP 可以通过议价交易获取更多的电能销售利润，购电VPP 可以通过议价交易降低电能的购买成本。

此外，VPP独立运行与合作运行偏差电量如图2所示。由图可知，相比VPP独立运行，VPP合作运行时的偏差电量在各时段普遍减少，即VPP 的对外出力会与PCC 的需求更加接近。因此，多VPP 合作运行对提升总体经济性有着积极作用。

图2 VPP独立运行与合作运行偏差电量Fig.2 Deviation electric quantity of VPP independent operation and cooperative operation

4.2.2 网络相关约束与过网费分摊机制设定分析

在附录C 图C1 所示系统结构下，考虑、不考虑网络相关约束的情况时VPP3与其他VPP 的直接交互功率δPVPP3，i如图3所示。不考虑网络相关约束的情况时，当VPP3与VPP4的物理连接发生改变，不再直接相连时，优化结果为图3（a）所示，即VPP4仍与VPP1—VPP3发生直接交易。此外，在第9 时段VPP3与VPP4直接交易在线路中传输功率为273.17 kW，超出线路最大传输限制，上述优化结果不符合实际情况。如果考虑网络相关约束，则VPP3的直接交易策略为图3（b）所示，即VPP4不会与VPP1—VPP3发生直接交易，由于考虑了网络阻塞约束，优化结果不会超出线路最大传输限制。因此，日前电能交易模型必须考虑网络相关约束。

图3 2种情况下VPP3与其他VPP的直接交互功率Fig.3 Direct transaction power of VPP3 with other VPPs in two cases

过网费的设计对于市场参与者的策略选择具有指导作用［21-22］。表1、2 分别为不同过网费承担机制下的VPP交易收益情况和各VPP需承担的过网费金额，可知过网费成本不可忽视。结合附录C 图C4 不同过网费分摊模式下VPP 直接交易电量结果可知，造成上述结果的主要原因是各市场参与者的收益不仅包含出售电能的收入，还需扣除向主网缴纳的过网费。由于过网费与市场参与主体的购售电报价存在耦合关系：对购电侧而言，其报价下限为边际运维成本与其承担的单位过网费之和，倘若过网费仅由售电侧独自承担，则其最低报价会大幅升高，报价允许范围变小；对售电侧而言，其报价的上限为内部可调节单元的调用边际成本与单位过网费之差，倘若过网费仅由购电侧独自承担，则其最高报价会大幅下降，报价允许范围变小。报价允许范围变小所导致的直接结果是报价被目标交易对象接受的几率下降，即VPP直接交易量会减少，相应整体收益会有所下降。

表1 不同过网费承担机制下的VPP交易收益Table 1 Profit of VPP transaction under different undertake mechanism单位：元

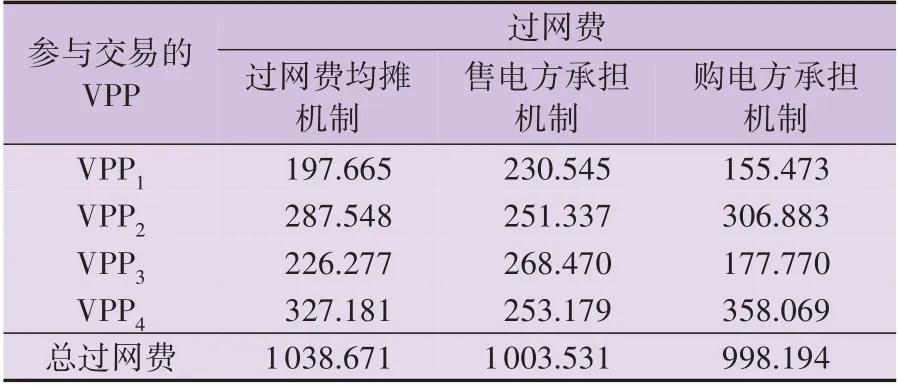
表2 不同过网费承担机制下的过网费金额Table 2 Amount of network fee under different allocation mechanism单位：元

综上，在本文背景下无论是考虑到VPP 联盟的整体经济性还是电网的过网费收益，过网费均摊机制均为最有利的选择。

4.2.3 基于效用理论的不确定性处理分析

在允许VPP 间直接交易、遵循过网费均摊机制的前提下，对以下6种策略结果进行分析：①策略1，综合考虑经济性以及VPP可调节单元与不可调节单元风险水平，制定日前上报曲线计划；②策略2，综合考虑经济性以及VPP 不可调节单元风险水平，制定日前上报曲线计划；③策略3，仅考虑经济性最优制定日前上报曲线计划；④策略4，综合考虑经济性以及风险，VPP 风险偏好程度固定，=0.2；⑤策略5，综合考虑经济性以及风险，VPP 风险偏好程度固定，=0.5；⑥策略6，综合考虑经济性以及风险，VPP风险偏好程度固定，=0.8。

定义24 h 总体经济收益Ctotal=C1-Closs-C2，即其值为日前计划的理想经济收益C1与最终结算损失函数Closs以及实时调节附加成本C2之差。对以上策略分别进行模拟优化，表3 对比了所模拟10 000种场景下不同策略的总经济收益情况。表中：Xmn为策略m与策略n的总体经济收益之比；Pr（Xmn>1）为Xmn>1时的概率。

表3 不同策略间的总体经济收益情况对比Table 3 Comparison of total economic profit among different strategies

由表3 可知，综合考虑经济性以及可调节单元与不可调节单元风险水平制定日前上报曲线的总体经济收益在多数情况下都优于不考虑可调节单元风险水平的策略2 或仅考虑经济性最优的策略3 和整体风险偏好程度固定的策略4 —6。由此，验证了所提同时考虑不可调节单元与可调节单元的风险水平计算方法的有效性和优越性以及考虑风险水平的日前VPP 电能交易模型的合理性。附录C 图C5 显示了本文采取的策略1下各VPP的风险效用水平。

4.2.4 变时间尺度策略优化结果分析

实时阶段每个结算周期的变时间尺度优化问题求解所需时间约为1.12 s，远小于结算周期15 min，求解效率能够满足要求。选取VPP1具有典型性的时段5［04:00，05:00］进行具体分析，附录C 表C3 显示了该时段中实时调度策略及其选择依据。时段［04:00，04:15）的偏差为4.54 %，小于设定阈值5 %，故直接以基础尺度进行调节。而在［04:15，05:00］中包含的3 个基础时段的前时段调度结果与上报曲线的偏差均大于设定阈值5 %，故需对当前时段的调度策略进行讨论和选择。根据计算结果可知，时段［04:15，04:30）采用缩小尺度调节相比采用基础尺度调节，其偏差减小率为2.70 %，成本增加率为1.69 %，偏差减小率大于成本增加率，最终选取以缩小尺度进行调度；对于时段［04:30，04:45）与时段［04:45，05:00］，采取缩小尺度进行调节偏差均有所下降，但调度成本上升率相对较为大幅，高于偏差减小率，故最终都选择维持基础调节时间尺度。

进一步对VPP1以基础时间尺度、缩小时间尺度、变时间尺度调度进行比较，3 种实时调度方案的总调度成本分别为5 971.198、6 175.358、6 105.962元，这是因为以缩小时间尺度进行调度意味着可能会增加可中断负荷的开断次数和储能单元的有效充放电次数，从而可能产生额外的损耗成本。

选取不同偏差评价指标对VPP1在3种实时调度方案下实际对外出力与上报功率曲线偏差进行评价，具体结果如附录C 表C4 所示。结合总调度成本统计结果可知，缩小实时调节时间尺度对于降低实时环节与日前上报曲线的偏差具有积极作用，但频繁的调节可能会带来较高的调节成本。

综上，本文所提变时间尺度优化方法能够对实时调节时间尺度进行灵活优化决策，实现了降低调节成本与减小调度偏差的协调优化。

5 结论

本文提出了多VPP日前随机博弈与实时变时间尺度协同优化方法。首先基于效用理论，提出VPP风险偏好程度量化方法，通过计算各时段各VPP 的风险效用水平，为VPP 日前交易上报曲线的制定提供参考。接着考虑了网络相关约束、VPP 直接交易报价动态约束等，建立了VPP 日前电能交易模型。最后，兼顾控制调节成本以及减小与上报曲线偏差，建立了实时变时间尺度优化调度模型，通过仿真验证得到以下结论：

1）所提基于效用理论的VPP风险偏好量化方法同时考虑了可调节单元和不可调节单元的风险效用，使得风险量化更为全面，能够适应VPP多种不确定运行场景；

2）对VPP 间的直接交易进行网络约束，保证了VPP 在实际应用中的物理可行性，考虑过网费与报价耦合关系约束，对过网费的分摊机制进行合理规定，促进了VPP直接交易的实施，兼顾了区域电网和主网的获益；

3）所提实时变时间尺度优化策略能够实现在各调度时间尺度的灵活合理切换，兼顾了调节成本的控制与调度偏差的减小，在保证系统经济运行的同时提升了功率曲线的跟踪能力。

附录见本刊网络版（http：//www.epae.cn）。